Some Random Coincidence Point and Common Fixed Point Results in Cone Metric Spaces Over Banach Algebras

JIANG Bing-hua, CAI Ze-lin, CHEN Jin-yang

(School of Mathematics and Statistics, Hubei Normal University, Huangshi, 435002, China)

Abstract: In this paper, we obtain some tripled common random fixed point and tripled random fixed point theorems with several generalized Lipschitz constants in such spaces. We consider the obtained assertions without the assumption of normality of cones. The presented results generalize some coupled common fixed point theorems in the existing literature.

Key words: Tripled random fixed point; Tripled random coincidence point; Cone metric space over Banach algebra; Generalized Lipschitz constant; Tripled common random fixed point

§1. Introduction

Fixed point theory plays a basic role in applications of many branches of mathematics.Finding the fixed point of contractive mapping becomes the center of strong research activity(see [3, 8-10, 19, 21, 30, 35]). In 2007 Huang and Zhang[15]introduced cone metric space and proved some fixed point theorems of contractive mappings in such spaces. Since then,some authors proved lots of fixed point theorems for contractive or expansive mappings in cone metric spaces that expanded certain fixed point results in metric spaces, (see[1, 2, 5, 11, 13, 20,26, 31]). Hassen[7]introduced tripled fixed point of w-compatible mappings in abstract metric spaces and coupled coincidence point and common coupled fixed point results in cone metric spaces. However, latterly, some authors made a conclusion that fixed point results in cone metric spaces are just equivalent to those in metric spaces (see [4, 6, 22, 32]). But fortunately,very recently, Liu and Xu[24]introduced the concept of cone metric space over Banach algebra and proved the non-equivalence of fixed point results in these new spaces and usual metric spaces. As a result, it is essentially necessary to investigate fixed point results in cone metric spaces over Banach algebras. Random coincidence point theorems are stochastic generalizations of classical coincidence point theorems, and play an important role in the theory of random differential and integral equations. Random fixed point theorems for contractive mapping on complete separable metric space have been proved by several authors (see [17, 23]). ´Ciri´c[12]and Zhu [37]proved some coupled random fixed point and coupled random coincidence results in partially ordered metric spaces. Afterwards, many coupled random coincidence results in partially ordered metric spaces were considered (see [16, 34]). In this paper, we obtain tripled common random fixed point and tripled random fixed point theorems with several generalized Lipschitz constants in cone metric spaces over Banach algebras by omitting the normality of cones. The presented results improve the main results of [7]in a large extent.

§2. Preliminaries

Let A be a Banach algebra with a unit e, and θ the zero element of A. A nonempty closed convex subset P of A is called a cone if

(i) {θ,e}⊂P;

(ii ) P2=PP ⊂P,P(−P)={θ};

(iii) λP +µP ⊂P for all λ,µ≥0.

On this basis, we define a partial orderingwith respect to P by xy if and only if y −x ∈P. We shall write xy to indicate that xy but xy, while xwill indicate that y −x ∈intP, where intP stands for the interior of P. Writeas the norm on A. A cone P is called normal if there is a number M >0 such that for all x,y ∈A,

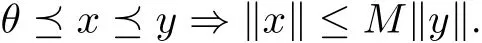
The least positive number satisfying above is called the normal constant of P.

In the following we always suppose that A is a Banach algebra with a unit e. P is a cone in A with intP∅, andis a partial ordering with respect to P.

Definition 2.1[24]Let X be a nonempty set and A a Banach algebra. Suppose that the mapping d:X ×X →A satisfies:

(i) θ ≺d(x,y) for all x,y ∈X withand d(x,y)=θ if and only if x=y;

(ii) d(x,y)=d(y,x) for all x,y ∈X;

Then d is called a cone metric on X, and (X,d) is called a cone metric space over Banach algebra A.

Example 2.2[24]Let A =MnR = {a = (aij)n×n|aij∈R} for all 1 ≤i,j ≤n be the algebra of all n-square real matrices, and define the norm

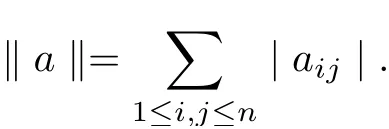
Then A is a real Banach algebra with the unit e, the identity matrix. Let P ={a ∈≥0 for all 1 ≤i,j ≤n}. Then P ⊂A is a normal cone with a normal constant M = 1. Let X =MnR, and define the metric d=X ×X −→A by

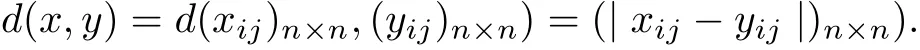
Then (X,d) is a cone metric space with a Banach algebra A.

Definition 2.3[36]Let (X,d) be a cone metric space over Banach algebra, x ∈X and{xn} a sequence in X. Then

(i) {xn} converges to x whenever, for every c ∈E withthere is a natural number N such that d(xn,x)c for all n ≥N. We denote this by=x or xn→x(n →∞).

(ii) {xn} is a Cauchy sequence whenever, for every c ∈E withthere is a natural number N such that d(xn,xm)c for all n,m ≥N.

(iii) (X,d) is complete if every Cauchy sequence is convergent.

The following lemmas are often used (in particular when dealing with cone metric spaces in which the cones need not be normal).

Lemma 2.4[36]Let (X,d) be a cone metric space over Banach algebra A and P a cone in A. Then the following properties are often used.

Lemma 2.5[29]Let A be a Banach algebra with a unit e, x ∈A, thenexists and the spectral radius ρ(x) satisfies

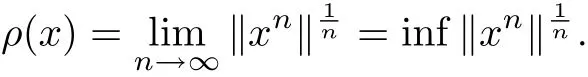
If ρ(x)<|λ|, then λe −x invertible in A, moreover,

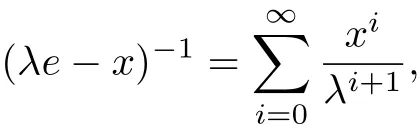
where λ is a complex constant.

Lemma 2.6[29]Let A be a Banach algebra with a unit e,a,b ∈A. If a commutes with b,then

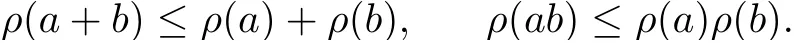
Definition 2.7[33]An element (x,y,z) ∈X3is said to be a tripled fixed point of the mapping F :X3→X if F(x,y,z)=x,F(y,z,x)=y, and F(z,x,y)=z.

Note that if (x,y,z) is a tripled fixed point of F, then (y,z,x) and (z,x,y) are tripled fixed points of F too.

Definition 2.8[33]An element (x,y,z)∈X3is called

(1)a tripled coincidence point of the mapping F :X3→X and g :X →X if F(x,y,z)=gx,F(y,z,x)=gy,F(z,x,y)=gz, and (gx,gy,gz) is called a tripled point of coincidence;

(2) a common tripled fixed point of mapping F : X3→X and g : X →X if F(x,y,z) =

gx=x, F(y,z,x)=gy =y and F(z,x,y)=gz =z.

Definition 2.9[2]The mapping F :X3→X and g :X →X are called w-compatible provided that gF(x,y,z)=F(gx,gy,gz)whenever F(x,y,z)=gx,F(y,z,x)=gy and F(z,x,y)=gz.

Let (Ω,Σ) be a measurable space with Σ a sigma algebra of subsets of Ω and let (X,d)be a metric space. A mapping T : Ω →X is called Σ-measurable if for any open subset U of X, T−1(U) = {ω : T(ω) ∈U} ∈Σ. In what follows, when we speak of measurability we shall mean Σ-measurability. A mapping T :Ω×X →X is called a random operator if for any x ∈X,T(·,x) is measurable. A measurable mapping ξ :Ω →X is called a random fixed point of a random operator T :Ω×X →X, if ξ(ω)=T(ω,ξ(ω)) for every ω ∈Ω.

Definition 2.10[18]Let (X,d) be a separable metric space and (Ω,Σ) be a measurable space. Then F :Ω×X3→X and g :Ω×X →X are said to be w-compatible random operators if

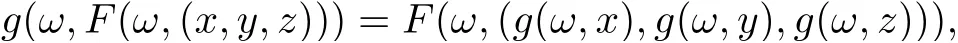
whenever F(ω,(x,y,z)) = g(ω,x),F(ω,(y,z,x)) = g(ω,y),F(ω,(z,x,y)) = g(ω,z) for all ω ∈Ω and x,y,z ∈X are satisfied.

Lemma 2.11[36]Let P be a cone in a Banach algebra A and k ∈P be a given vector. Let{un} be a sequence in P. If for eachthere exist N1such thatfor all n>N1,then for each, there exist N2such that kunfor all n>N2.

Now, we state our main results as follows.

§3. Main Results

In this section, we prove some tripled random coincidence and tripled random fixed point theorems for contractive mappings with several generalized Lipschitz constants in the setting of cone metric spaces over Banach algebras by deleting the normality of cones.

Lemma 3.1[36]Let A be a Banach algebra and k ∈A. If ρ(k)<1, then.

Remark 3.2If<1, it is natural that ρ(k)<1, yet, the converse is not true.

Lemma 3.3[36]Let A be a Banach algebra with a unit e, {xn} a sequence in A. If {xn}converges to x in A , and for any n ≥1, {xn} commutes with x, then ρ(xn)→ρ(x) as n →∞.

Theorem 3.4Let(X,d)be a separable cone metric space over Banach algebra A, P be a cone in A and (Ω,Σ) be a measurable space. Suppose that the mappings and F :Ω×X3→X and g :Ω×X →X satisfy the following contractive condition:

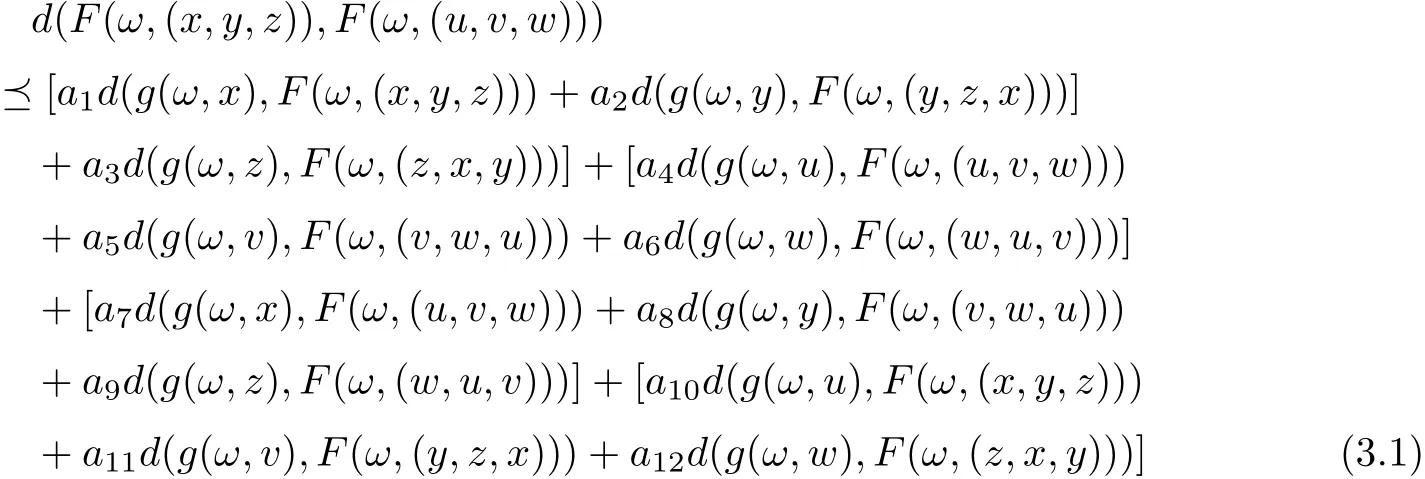
for all x,y,z,u,v,w ∈X, where ai∈P,aiaj= ajai(i,j = 1,...,15), aiare generalized Lipschitz constants with ρ(a1+a2+a3)+ρ(a4+···+a9)+ρ(a10+a11+a12)<1. Let F(·,v),g(·,x)be measurable for v ∈X3and x ∈X, respectively. Suppose that F(ω×X3) ⊆g(ω×X) and g(ω ×X) is a complete subspace of X for each ω ∈Ω. Then there exist mappings ξ,η,θ :Ω →X such that F(ω,(ξ(ω),η(ω),θ(ω))) = g(ω,ξ(ω)), F(ω,(η(ω),θ(ω),ξ(ω))) = g(ω,η(ω))and F(ω,(θ(ω),ξ(ω),η(ω)))=g(ω,θ(ω)) for all ω ∈Ω, that is, F and g have a tripled random coincidence point.

ProofLet Θ = {η : Ω →X} be a family of measurable mappings. We construct three sequences of measurable mappings {ξn}, {ηn}, {θn} in Θ and three sequences {g(ω,ξn(ω))},{g(ω,ηn(ω))}, {g(ω,θn(ω))} in X as follows.

Let ξ0,η0,θ0∈Θ. Since F(ω,(ξ0(ω),η0(ω),θ0(ω))) ∈F(ω×X3) ⊆g(ω×X), by a sort of Filippov measurable implicit function theorem(see[35]),there is ξ1∈Θ such that g(ω,ξ1(ω))=F(ω,(ξ0(ω),η0(ω),θ0(ω))). Similarly as F(ω,η0(ω), θ0(ω)ξ0(ω))) ∈g(ω×X), there is η1∈Θ such that g(ω,η1(ω))=F(ω,(η0(ω),θ0(ω)ξ0(ω))),F(ω,(θ0(ω),ξ0(ω),η0(ω)))∈g(ω×X),there is θ1∈Θ such that g(ω,θ1(ω)) = F(ω,(θ0(ω),ξ0(ω),η0(ω))). Continuing this process we can construct sequences {ξn(ω)}, {ηn(ω)} and {θn(ω)} in X such that

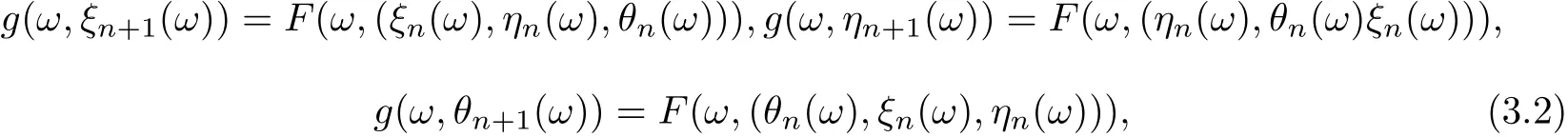
for all n ∈N. According to (3.1), we have

Further, we have

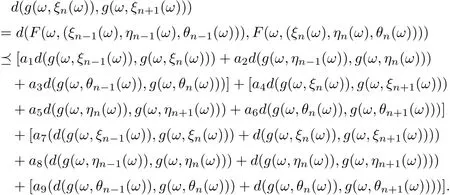
Hence, we obtain that

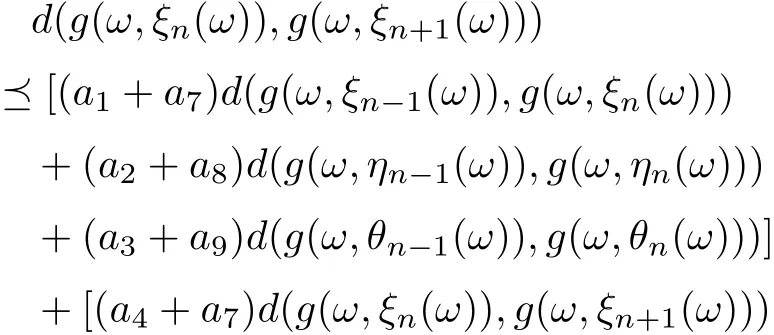
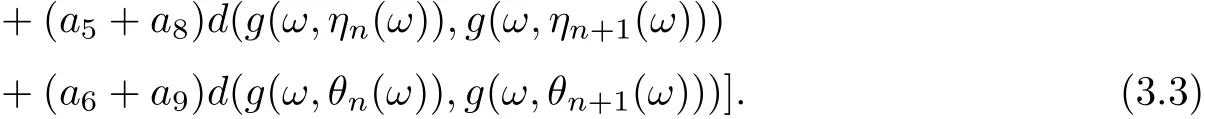
Similarly, we can prove that

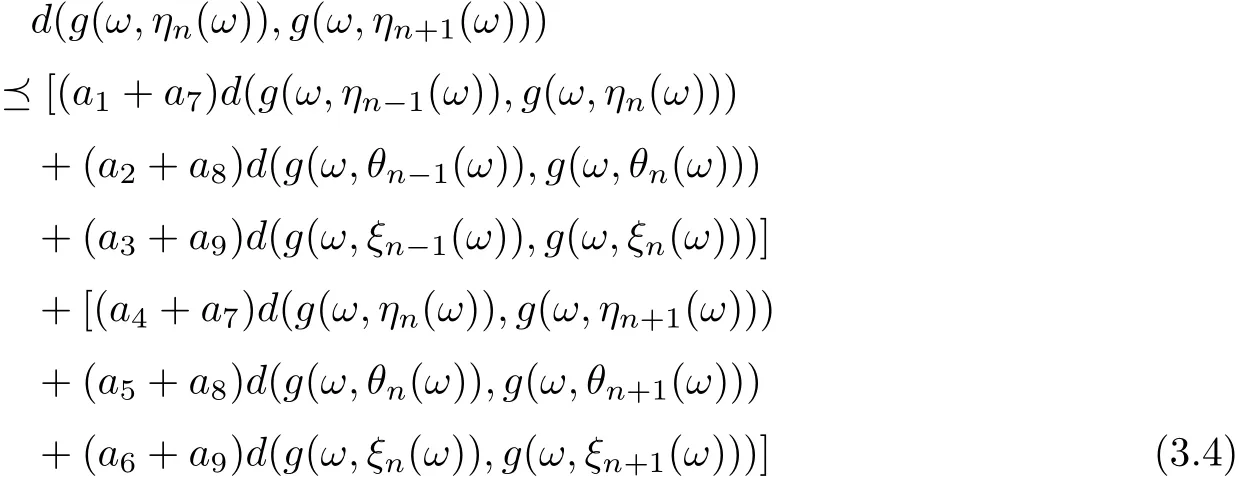
and

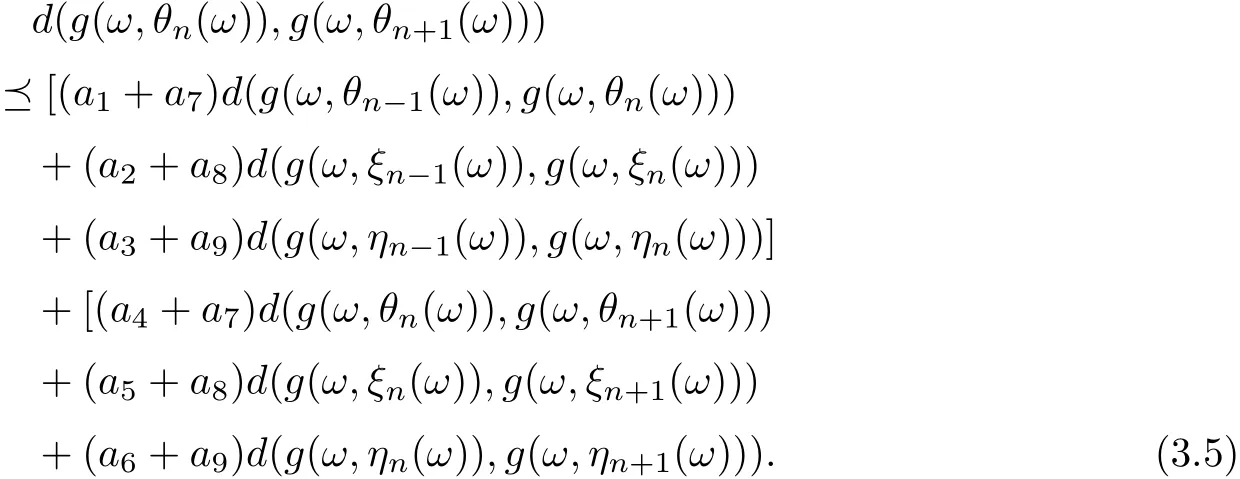
Put

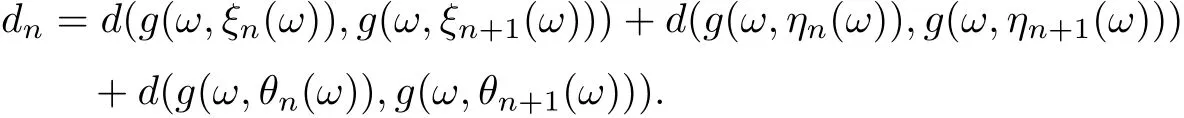
Uniting (3.3)-(3.5), ones assert that

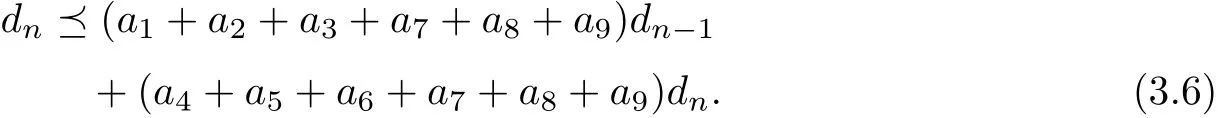
Furthermore,

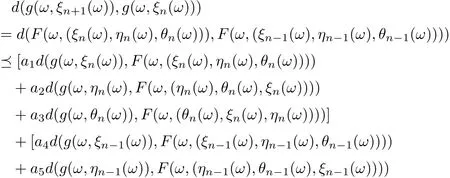
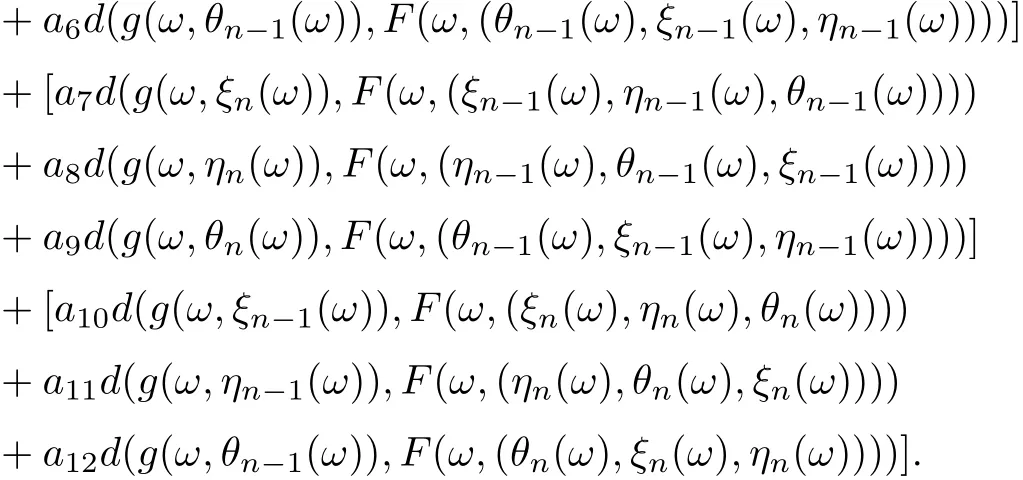
Then

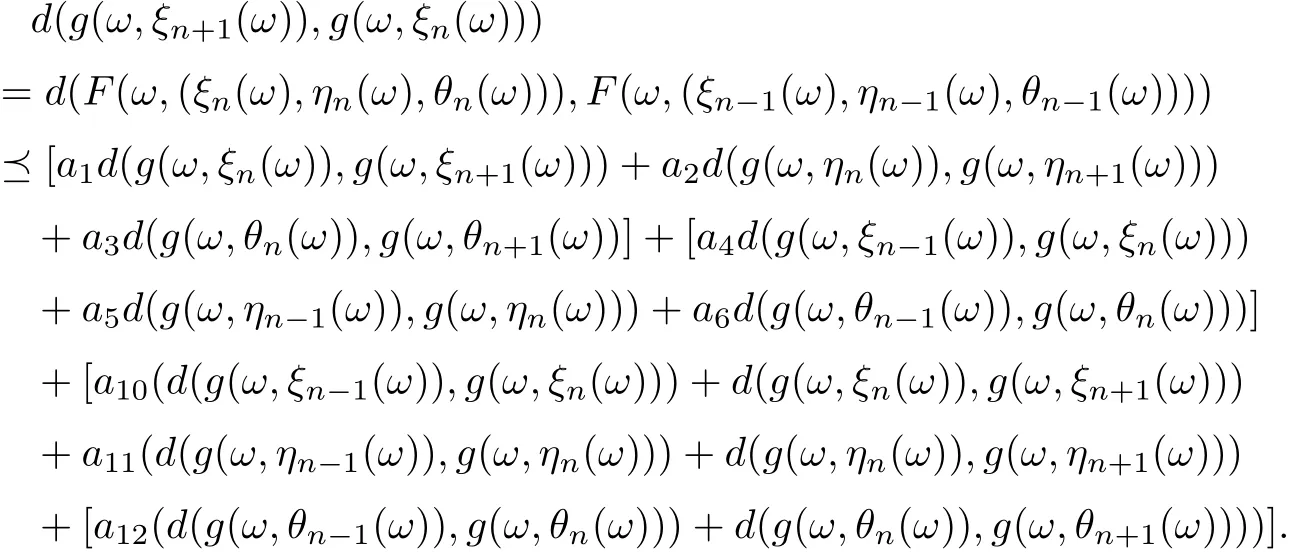
Accordingly, it is clear that

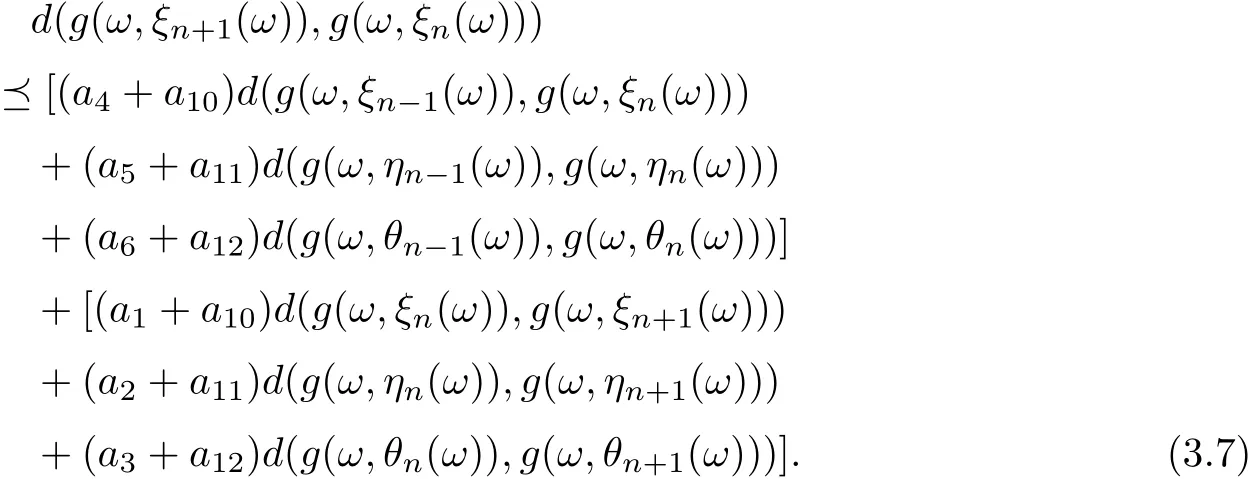
Similarly, we can prove that

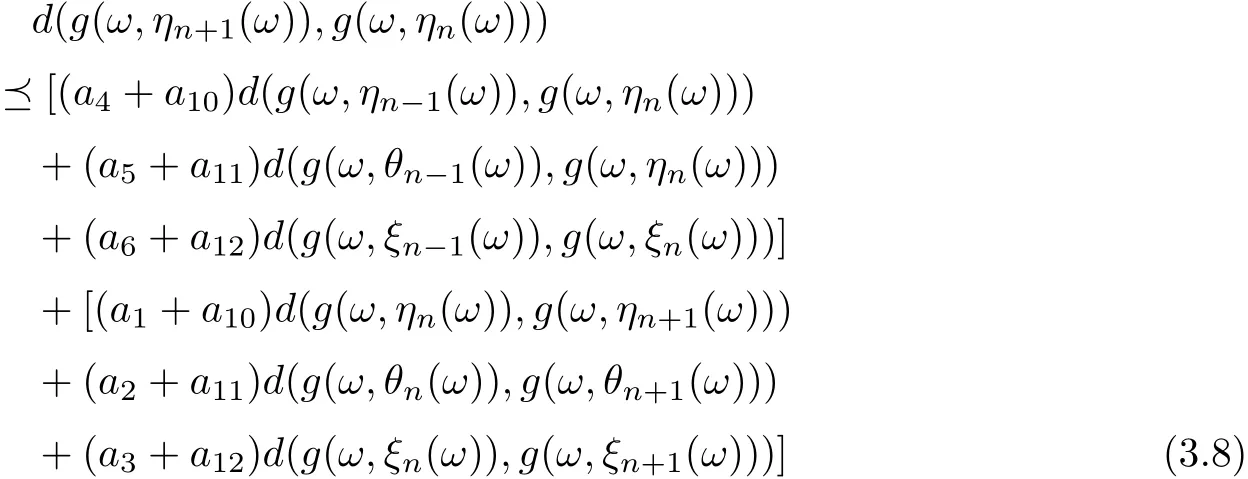
and

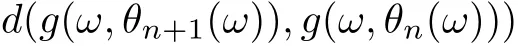
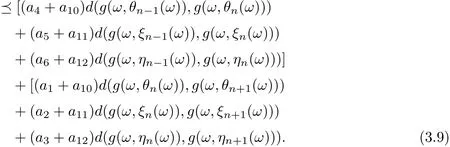
Uniting (3.7)-(3.9), one gets that

By using (3.6) and (3.10), it is easy to see that

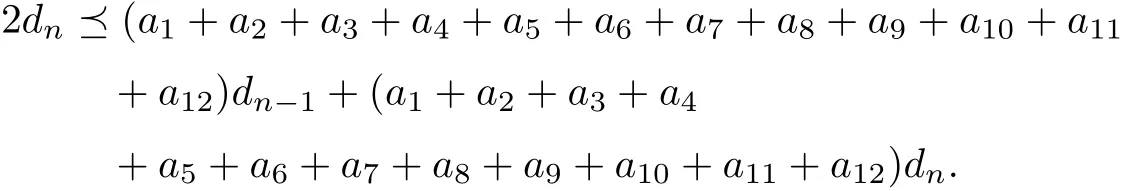
Then by Lemma 2.5 and Lemma 2.6, it follows that 2e −k is invertible. Furthermore,To multiply in both side of (3.11) by (2e −k)−1, we obtain

Denote h=(2e −k)−1k, then by (3.12) we get

Note by Lemma 2.6 that

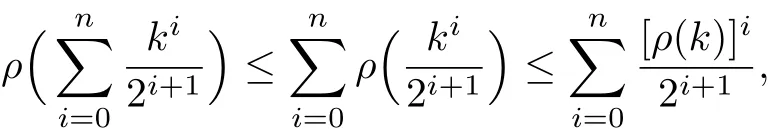
so by Lemma 3.3 it leads to

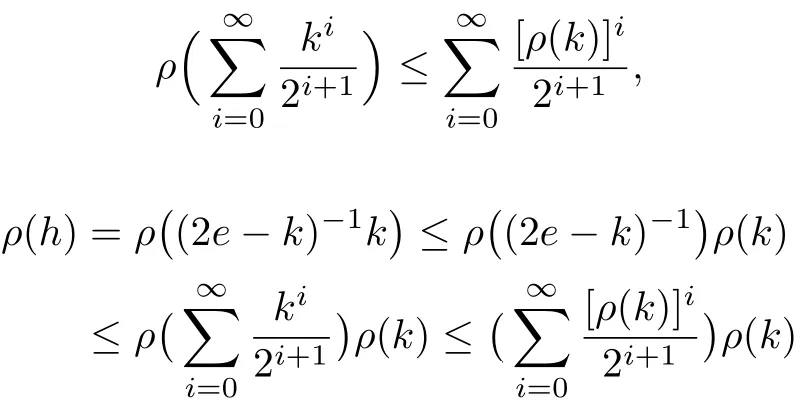
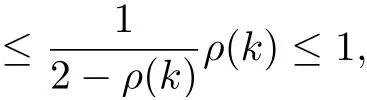
which establishes that e −h is invertible and→0 as n →∞. Thus for all m > n ≥1,ones have

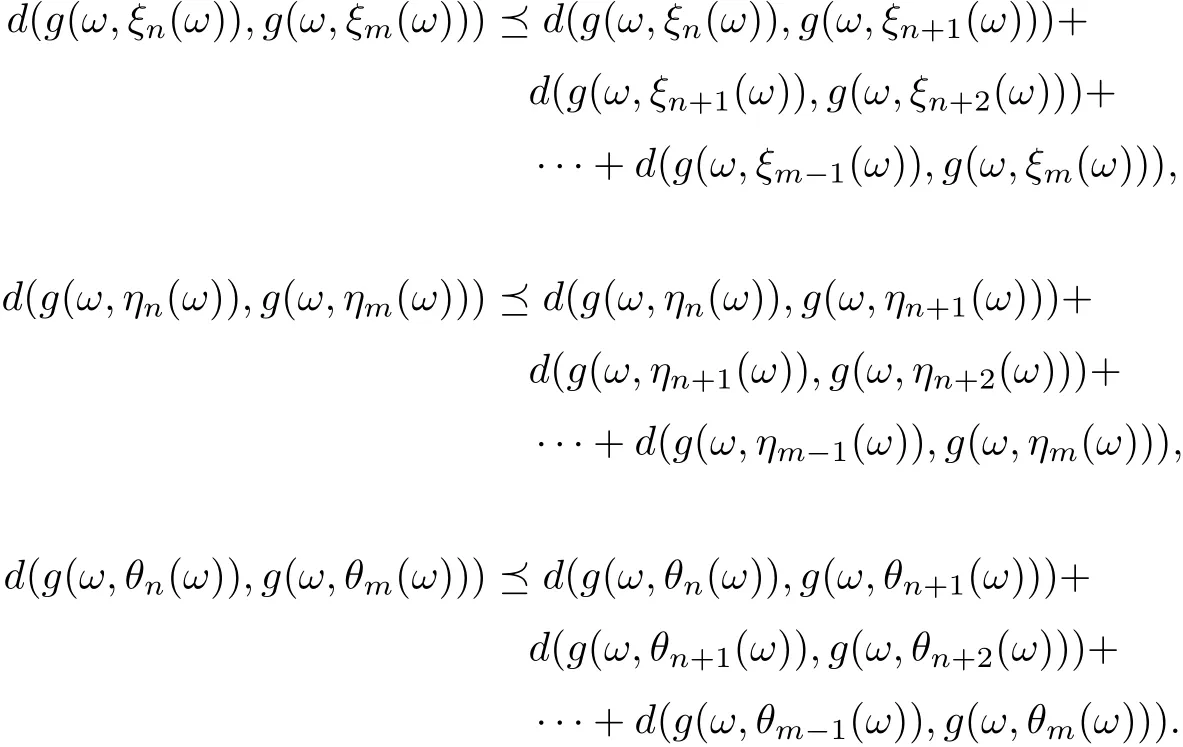
Now, by (3.13) and sρ(h)<1, it follows that

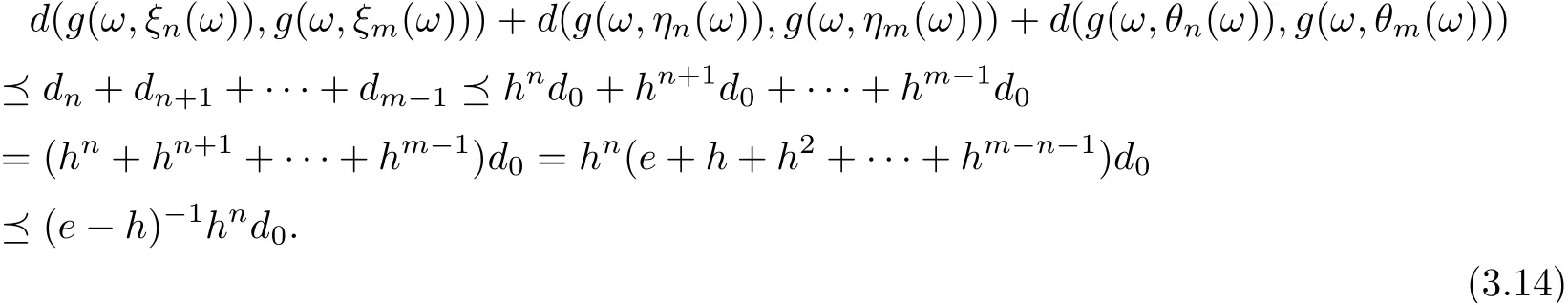
Owing to

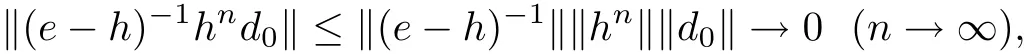
we have (e −h)−1hnd0→θ (n →∞).

According to Lemma 2.4, and for anythere exists N0such that for all n >N0, (e −h)−1hnd0Furthermore, from (3.14) and for any m > n > N0, it follows that d(g(ω,ξn(ω)),g(ω,ξm(ω)))+d(g(ω,ηn(ω)),g(ω,ηm(ω)))+d(g(ω,θn(ω)),g(ω,θm(ω)))which implies that d(g(ω,ξn(ω)),g(ω,ξm(ω)))c,d(g(ω,ηn(ω)),g(ω,ηm(ω)))d(g(ω,θn(ω)),g(ω,θm(ω))). Hence, {g(ω,ξn(ω))}, {g(ω,ηn(ω))}, {g(ω,θn(ω))} are Cauchy sequences in g(X). Since g(X) is complete, there exist ξ∗(ω),η∗(ω) and θ∗(ω) ∈X for all ω ∈Ω such that g(ω,ξn(ω)) →g(ω,ξ∗(ω)),g(ω,ηn(ω)) →g(ω,η∗(ω)),g(ω,θn(ω)) →g(ω,θ∗(ω)) as n →∞.Moreover, note that

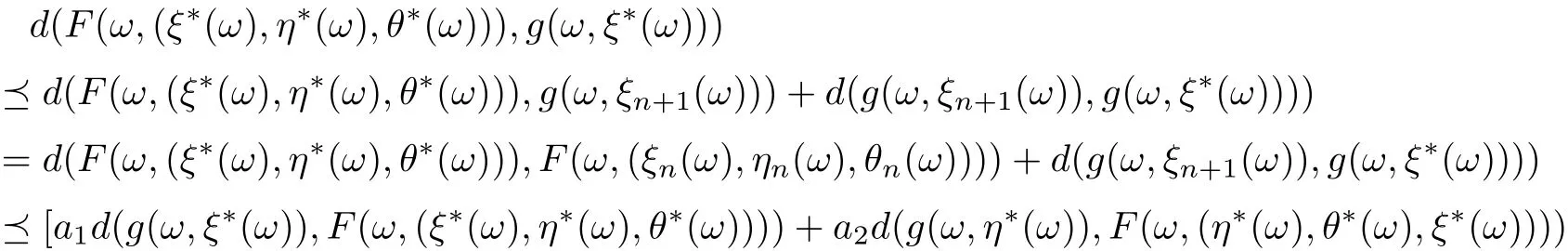
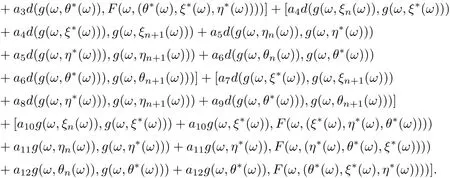
Hence, we get that

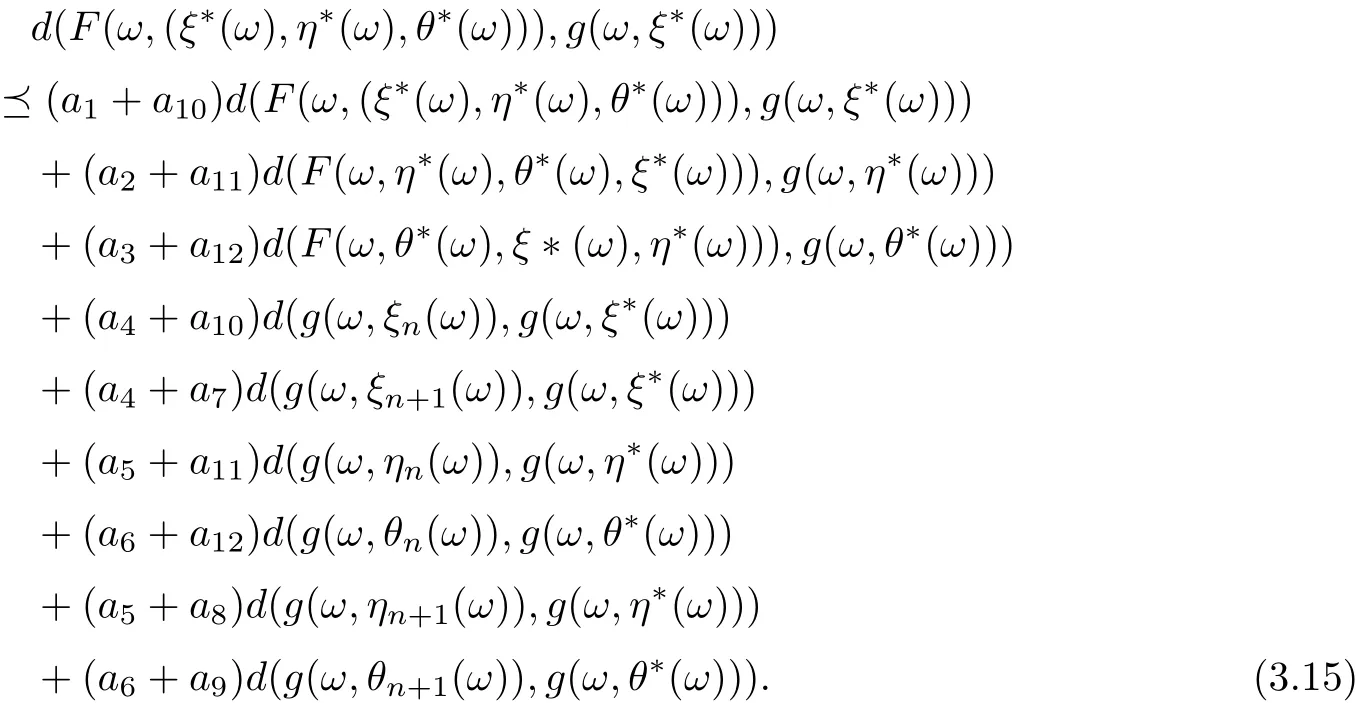
Similarly, it is easily obtain that

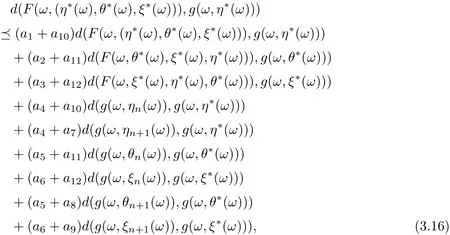
and

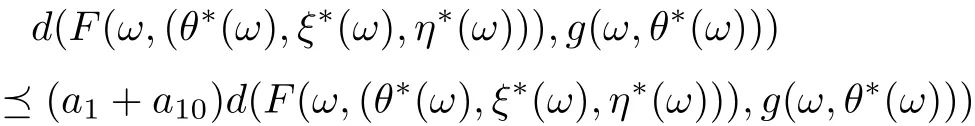
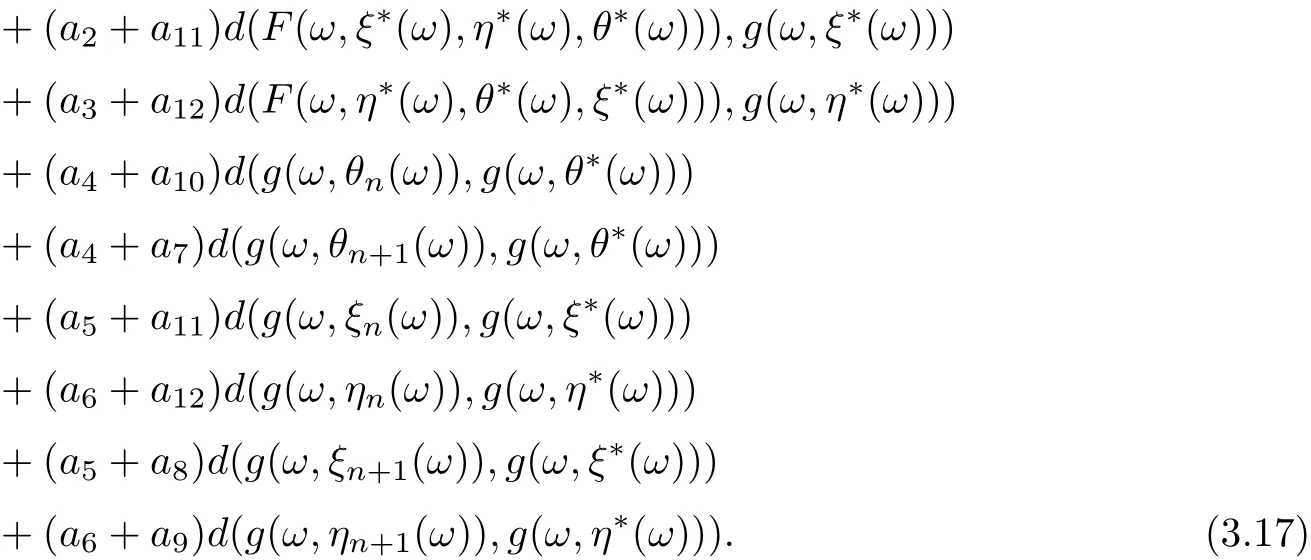
Put

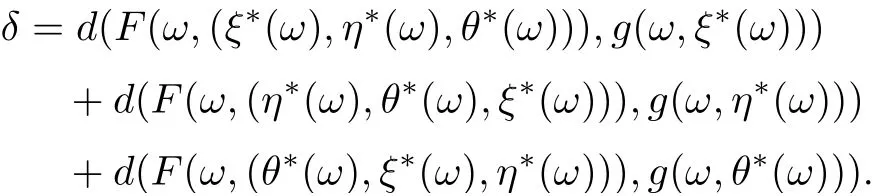
On view of (3.15)-(3.17), we get

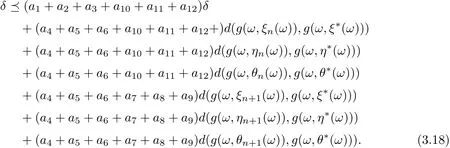
Then

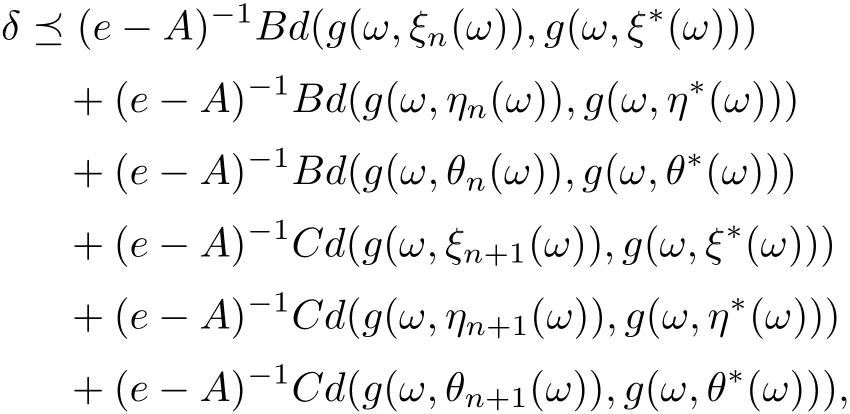
where A = a1+a2+a3+a10+a11+a12, B = a4+a5+a6+10+a11+12, C = a4+a5+a6+a7+a8+a9, ρ(A) ≤ρ(a1+a2+a3)+ρ(a4+···+a9)+ρ(a10+a11+a12) < 1. Since g(ω,ξn(ω))→g(ω,ξ∗(ω)),g(ω,ηn(ω))→g(ω,η∗(ω)),g(ω,θn(ω))→g(ω,θ∗(ω)),it follows that for any cθ, there exists N0such that for n>N0. Then by Lemma 2.11 we have

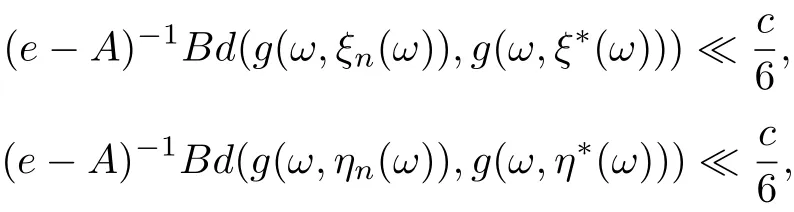
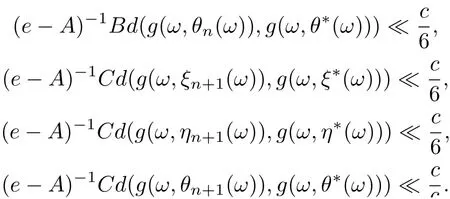
6

Hence,

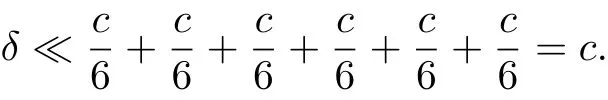
Now, according to Lemma 2.4, it follows that δ =θ, that is,

which implies that

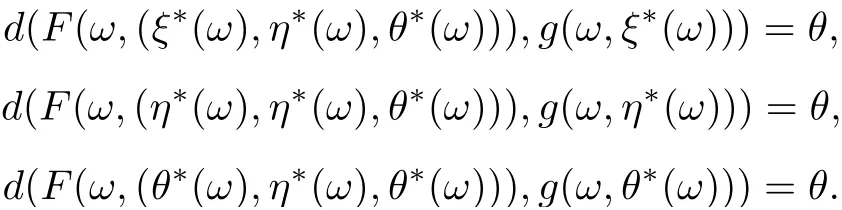
Thus,

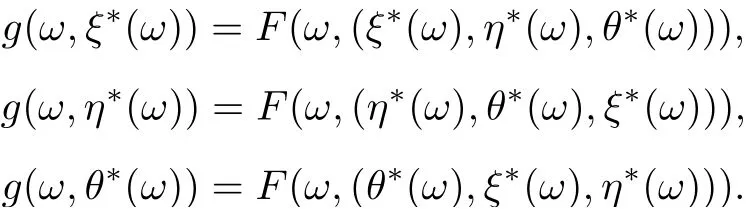
Therefore (ξ∗(ω),η∗(ω),θ∗(ω)) is a tripled coincidence point of F and g for all ω ∈Ω.

Corollary 3.5Let (X,d) be a separable cone metric space over Banach algebra A and P be a cone in A, (Ω,Σ) be a measurable space. Suppose that the mappings F :Ω×X3→X,g :Ω×X →X satisfy the following contractive condition:

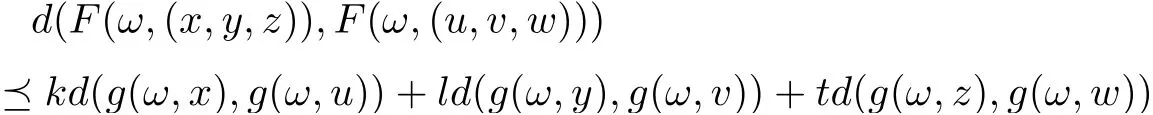
for all x,y,z,u,v,w ∈X,where k,l,t ∈P are generalized Lipschitz constant with ρ(k+l+t)<1,F(.,v),g(.,x) are measurable for v ∈X3and x ∈X, respectively, F(ω ×X3) ⊆g(ω ×X)and g(ω ×X) is complete subspace of X for each ω ∈Ω, then there are mappings ξ,η,θ :Ω →X, such that F(ω,(ξ(ω),η(ω),θ(ω))) = g(ω,ξ(ω)), F(ω,(η(ω),θ(ω),ξ(ω))) = g(ω,η(ω)),F(ω,(θ(ω),ξ(ω),η(ω))) = g(ω,θ(ω)) for all ω ∈Ω, that is F and g have a tripled random coincidence point.

Corollary 3.6Let (X,d) be a separable cone metric space over Banach algebra A, P be a cone in A and(Ω,Σ)be a measurable space. Suppose that the mappings F :Ω×X3→X,g :Ω×X →X satisfy the following contractive condition:

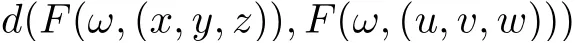
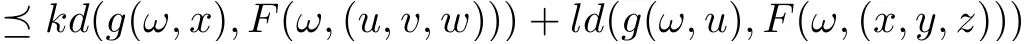
for all x,y,z,u,v,w ∈X,where k,l ∈P are generalized Lipschitz constants with ρ(k)+ρ(l)<1,F(·,v),g(·,x) are measurable for v ∈X3and x ∈X, respectively, F(ω ×X3) ⊆g(ω ×X)and g(ω ×X) is complete subspace of X for each ω ∈Ω, then there are mappings ξ,η,θ :Ω →X, such that F(ω,(ξ(ω),η(ω),θ(ω))) = g(ω,ξ(ω)), F(ω,(η(ω),θ(ω),ξ(ω))) = g(ω,η(ω)),F(ω,(θ(ω),ξ(ω),η(ω))) = g(ω,θ(ω)) for all ω ∈Ω, that is, F and g have a tripled random coincidence point.

The conditions of Theorem 3.4 are not enough to prove the existence of a common tripled fixed point for the mappings F and g. By restricting to w-compatibility for F and g, we obtain the following theorem.

Theorem 3.7In addition to hypotheses of Theorem 3.4, if F and g are w-compatible,then F and g have a unique tripled common fixed point. Moreover, a tripled common random fixed point of F and g is of the form (ξ∗(ω),ξ∗(ω),ξ∗(ω))∈X for all ω ∈Ω.

ProofBy Theorem 3.4,F and g have tripled random coincidence point(ξ∗(ω),η∗(ω),θ∗(ω)).Then (g(ω,ξ∗(ω)),g(ω,η∗(ω)),g(ω,(θ∗(ω))) is a tripled random point of coincidence of F and g such that

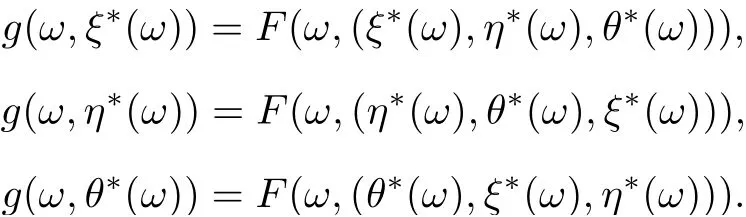
First, we shall show that the tripled random point of coincidence is unique. Suppose that F and g have another tripled random point of coincidence(g(ω,ξ∗∗(ω)),g(ω,η∗∗(ω)),g(ω,θ∗∗(ω)))such that

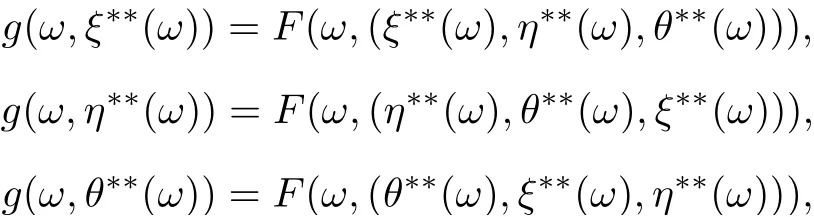
where (ξ∗∗(ω),η∗∗(ω),θ∗∗(ω))∈X3for all ω ∈Ω. Then we have

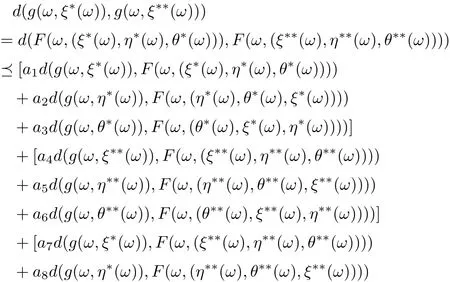
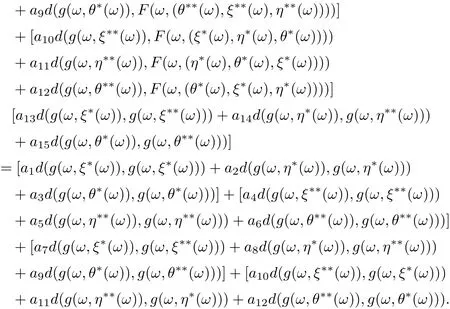
Hence,

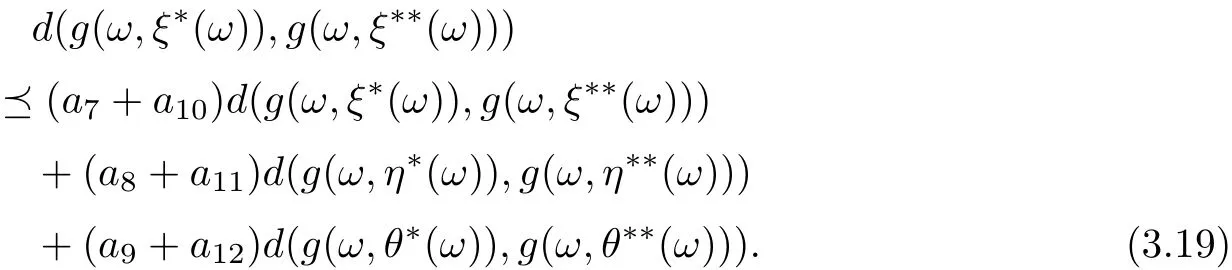
Similarly, we have

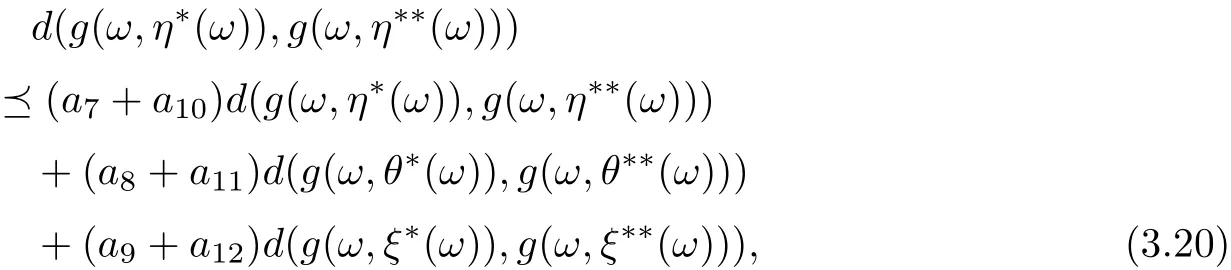
and

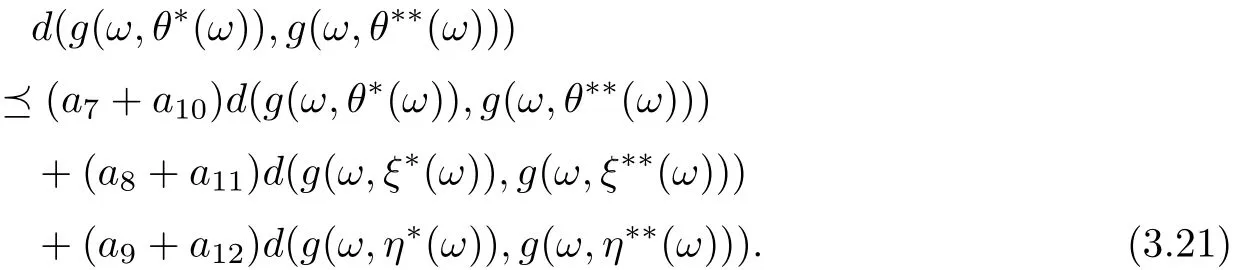
By combining (3.19)-(3.21), we get

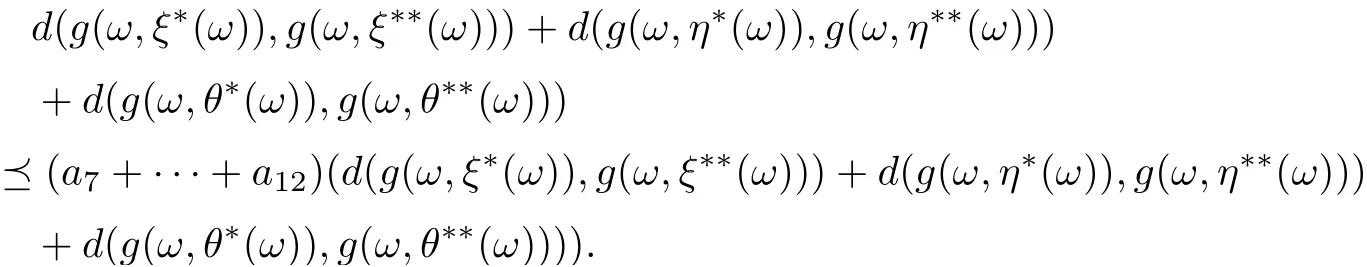
Set α=a7+···+a12, γ =d(g(ω,ξ∗(ω)),g(ω,ξ∗∗(ω)))+d(g(ω,η∗(ω)),g(ω,η∗∗(ω)))+d(g(ω,θ∗(ω)),g(ω,θ∗∗(ω))), we haveNow that ρ(α)<1,

which leads to αn→θ (n →∞), we claim that, for each c, there exists n0(c) such that αnc (n>n0(c)). Consequently by Lemma 2.11,

d(g(ω,ξ∗(ω)),g(ω,ξ∗∗(ω)))+d(g(ω,η∗(ω)),g(ω,η∗∗(ω)))+d(g(ω,θ∗(ω)),g(ω,θ∗∗(ω)))=θ.

Hence,

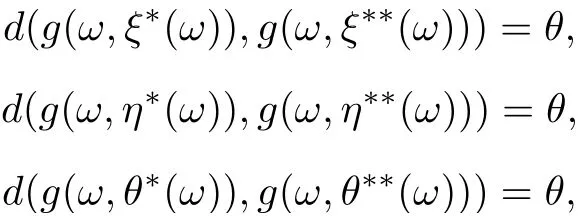
that is,

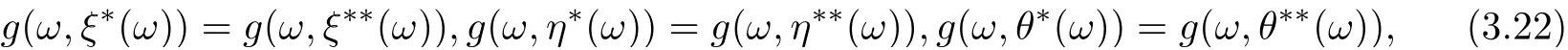
which implies the uniqueness of the tripled random point of coincidence of F and g. By a similar way, someone can prove that

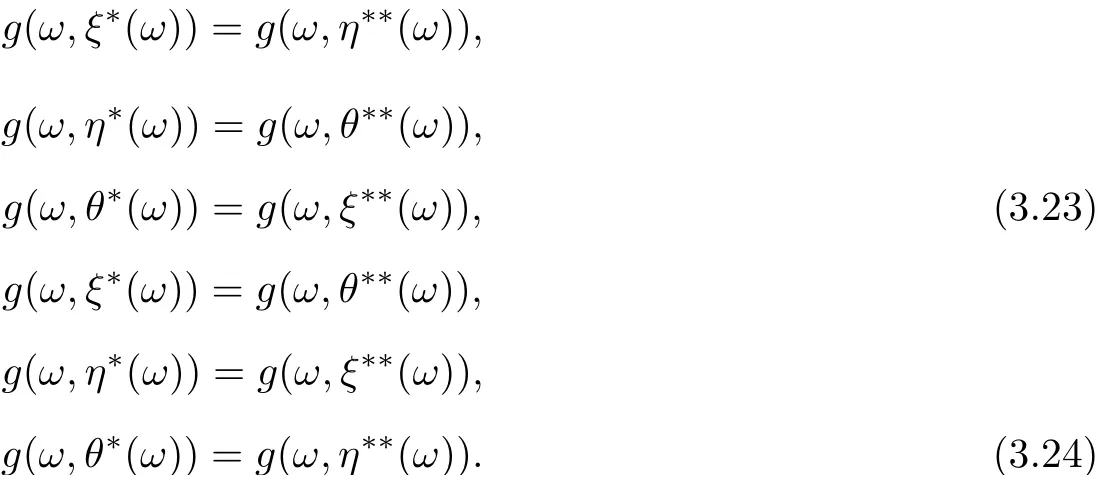
In view of (3.22)-(3.24), one can assert

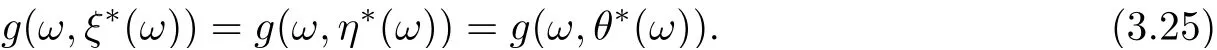
In other words, the unique tripled random point of coincidence of F and g is(g(ω,ξ∗(ω)),g(ω,η∗(ω)),g(ω,θ∗(ω))). Let u(ω) = g(ω,ξ∗(ω)) = F(ω,(ξ∗(ω)),η∗(ω)),θ∗(ω))).Since F and g are w-compatible, then we have

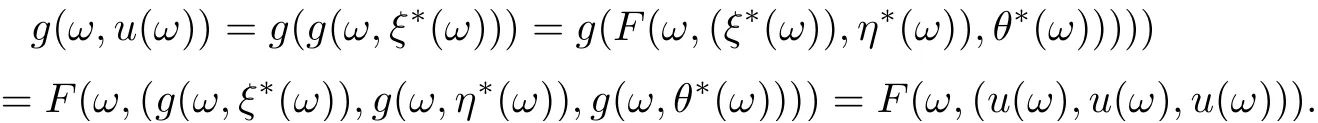
Thus (g(ω,u(ω)),g(ω,u(ω)),g(ω,u(ω))) is a tripled random point of coincidence. We also have (u(ω),u(ω),u(ω)) is a tripled random point of coincidence. Note that the uniqueness of the tripled random point of coincidence implies that g(ω,u(ω)) = u(ω). Therefore u(ω) =g(ω,u(ω)) = F(ω,(u(ω),u(ω),u(ω))). Hence (u(ω),u(ω),u(ω)) is the unique tripled common random fixed point of F and g for all ω ∈Ω. This completes the proof.

Putting g(ω,·)=I(ω,·)(identity mapping )in Theorem 3.4, we obtain the following result.The following example illustrates our conclusions.

Example 3.8Let X = R3, A = R3. For each x = (x1,x2,x3) ∈X, let|x1|+|x2|+|x3|, P ={(x1,x2,x3)∈R3|x1≥0,x2≥0,x3≥0}. The multiplication is defined by

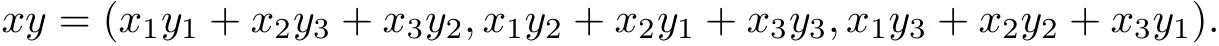
Then one can easily verify that A is a Banach algebra with unit e=(1,0,0). Can be observed,P is a cone in A. A metric d on X is defined by

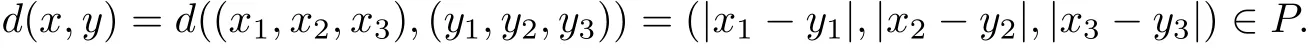
Easy to know (x,d) is a complete cone metric space over the Banach algebra A. Consider the following mapping g :Ω×X →X,g(ω,x)=((x1,2x2,3x3), for each (ω,(x1,x2,x3))∈Ω×X.Then g is a surjection. Define f :Ω×X3→X by

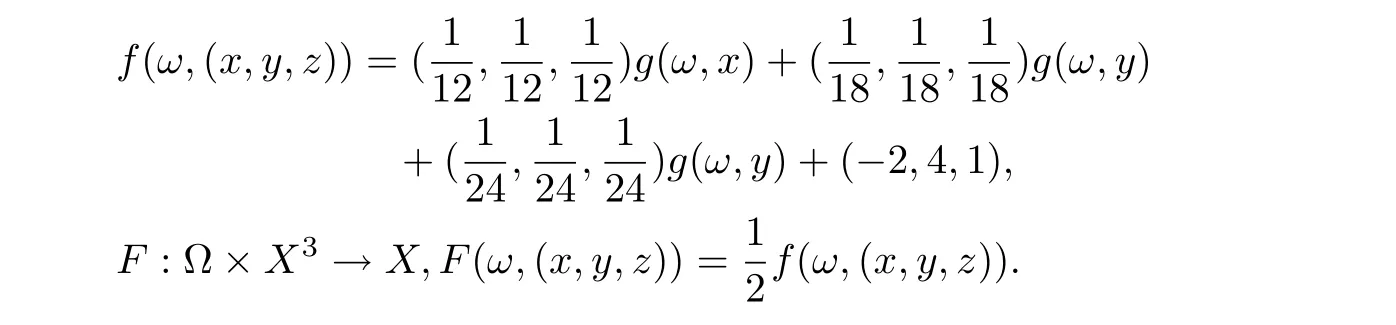
Firstly, easy to verify

(1) d(F(ω,(x,y,z)),F(ω,(u,v,w)))d(f(ω,(x,y,z)),f(ω,(u,v,w))).

(2) d(f(ω,(x,y,z)),f(ω,(x,y,z)))

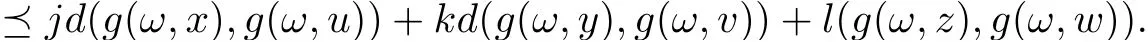
On the side, the following inequality naturally holds,

By (1),(2) and (3) have

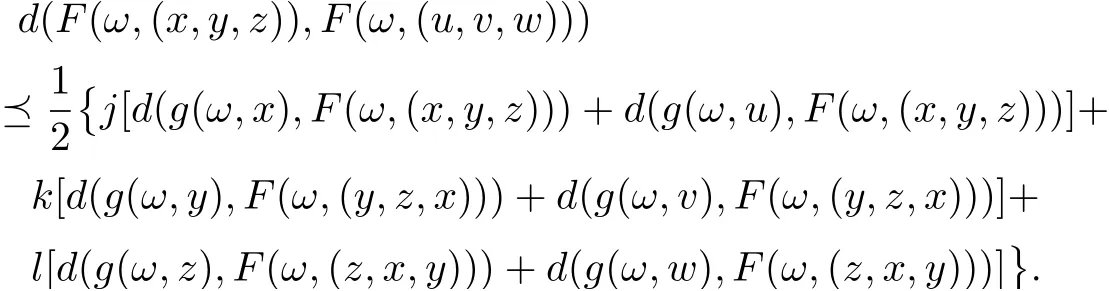
Get through theorem 3.4, we commandthat g,F immediately satisfy (3.1), and aiaj=ajai, (i,j =1,2...12), on the side,

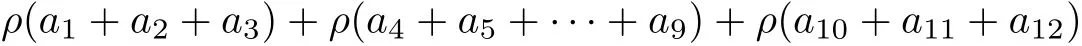
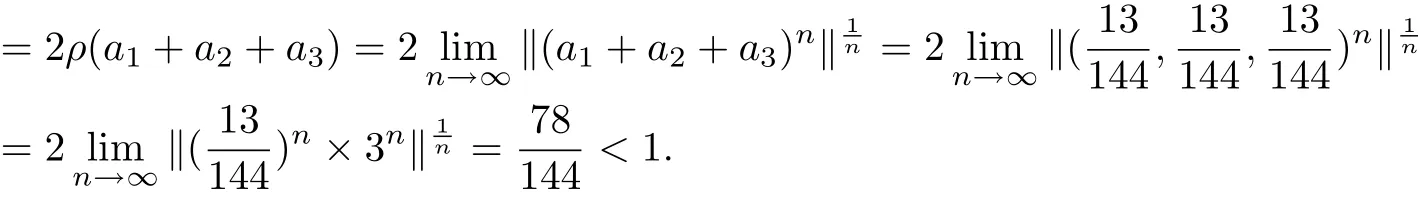
By Theorem 3.4 F and g have a tripled random coincidence point.

Remark 3.9Our main results mainly generalize the recent results. In fact, they never consider the normality of cones, which may offer us more applications since there exist lots of non-normal cones (see [28]). Moreover, we establish the contractive mappings with several generalized Lipschitz constants,where the constants are all vectors but not usual real constants.Thus they are different from some ordinary results and more interesting.

Remark 3.10Our theorems deal not only with common fixed point results with random process, but also with them from usual coupled fixed point to tripled fixed point. Therefore,our results greatly improve and extend some results in the literature (see [7]).

Remark 3.11Our results are mainly related to tripled random coincidence point and common fixed point results of generalized Lipschitz mappings in cone metric spaces over Banach algebras. Our tripled random coincidence point and common fixed point results cannot reduced to the counterparts of the results with one variable. In other words, the method of [22]cannot be utilized to our main results. This is because the generalized Lipchitz constants from our results are vectors. Moreover, the multiplication of the vectors do not satisfy the combinative law. Hence we cannot use a method of reducing our tripled results to the respective results for mappings with one variable.

Authors’ contributionsAll authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.