基于海上砂砾岩低渗透率成因分析及测井评价

张冲

(中海石油(中国)有限公司湛江分公司,广东湛江524057)

0 引 言

南海西部油田近年新发现的乌石东区流沙港组三段复杂砂砾岩储层,储层埋深2 300～3 000 m,属较为典型的扇三角洲砂砾岩沉积体系[1-2]。储层物性主要受沉积、成岩压实作用影响,储层物性展布规律复杂,相对高渗透率区是储层甜点。但由于流沙港组三段砂砾岩的低成分成熟度和低结构成熟度,岩石骨架、孔隙结构、基质和砾石含量差异大,储层渗透率的测井解释难度大,渗透率计算模型难以依据简单的统计规律进行构建,现有测井模型计算的储层渗透率解释精度低,不能满足油田开发需要。因此,本文基于孔隙结构参数定量表征的非线性储层渗透率精细计算方法,提高了复杂砂砾岩储层渗透率计算精度,对油田的进一步开发评价具有积极意义。

1 海上砂砾岩低渗透率成因分析

流沙港组三段岩性复杂,从粉砂岩、中细砂岩到砂砾岩均有分布,纵向上物性变化快,孔隙度、渗透率主要分布区间分别为15.0%～22.0%、4.0～64.0 mD(1)非法定计量单位,1 mD=0.987×10-3 μm2,下同,总体表现为中孔隙度、低渗透率特征。造成储层低渗透率的成因和物性的影响因素主要有以下3个方面。

(1)沉积因素。流沙港组三段沉积时期,乌石凹陷东区地形呈东高西低趋势,东北部发育北东—西南方向的沟道[3-4],为三角洲的注入提供了有利的搬运通道,河流携带着沉积物由地势高的地方往东北方向运移,在水动力变弱的时候,沉积物发生卸载沉积。沉积相带是造成储层物性差异和低渗透率的主要控制因素。乌石凹陷东区流沙港组三段是典型的扇三角洲水下分流河道特征[5],底部为砂砾岩储层以及槽状交错层理的含砾砂岩层;平行层理的中细砂岩和块状泥质粉细砂岩,在近物源处的水下分流河道由于分选磨圆差、泥质含量高,储层表现为低渗透率特征;稍微远离物源处的水下分流河道由于搬运距离更远,分选磨圆变好、泥质含量减少,储层渗透性变好。

(2)成岩压实作用。流三段随埋深加大,压实作用变强。岩石薄片表现为石英、长石等刚性颗粒定向排列,云母等塑性颗粒发生形变,碎屑颗粒以线-点状接触为主。研究区流沙港组三段压实率与孔隙度和渗透率呈一定的负相关关系,埋深增大,储层压实作用也越强,物性降低明显。深度2 600 m以下,综合压实率(含化学胶结压实)达70%以上,层内平均孔隙度低,低渗透率—特低渗透率,反映岩石进入强压实带。储层渗透率与埋深的关系显示,粗粒砂岩在埋深较大时,渗透率降低幅度大于细粒砂岩。

流沙港组三段压实胶结图从定量角度显示了不同井区的压实胶结作用强度,1区、9区、11区、14区埋深大,储层被压实作用消除的孔隙体积大,压实率高,属于强压实区,压实对储层物性具有明显的破坏作用。岩心壁心的物性分析也显示深埋区储层因埋深大压实作用强,储层物性尤其是储层渗透性明显降低。

(3)溶蚀和破裂作用。乌石凹陷东区流沙港组三段溶蚀作用产生大量的次生孔隙,扩大了储集空间,从铸体薄片下可以看到,长石溶孔、长石溶蚀形成的铸模孔十分常见,极大地改善了储层的孔隙空间。由于含砾砂岩因多晶石英砾石颗粒的存在,岩石脆性矿物含量高,在压实过程中,砾石颗粒的存在使砾石易发生扭动或破裂,渗透性有一定程度改善。正是因为局部储层受到溶蚀和破裂作用的影响,储层物性变化规律更为复杂。

基于海上砂砾岩低渗透率主控因素分析认为,储层渗透率的评价应考虑沉积、成岩作用塑造的孔隙结构和岩相类型两大因素。

2 基于孔隙结构参数的渗透率计算

2.1 砂砾岩储层岩相的划分

岩性变化大、多类岩性并存是砂砾岩储层的重要特征,由于岩相的变化,物性参数也会存在极大差异,特别是储层的渗透率,其差异可以达到2～3个数量级[6-7]。因此,精确的岩相划分是渗透率精细求解的基础。根据取心井岩性描述划分岩相剖面是最为直接和精确的方法,但对于海上油田而言,由于取心成本昂贵,岩心资料相对陆地油田显得极为匮乏,在无取心的井进行岩相划分就是问题的关键。不同的岩相往往具有不同的孔隙结构和复杂的成岩作用,因此,有必要利用较易获得的测井资料在纵向上对岩相进行识别和精确划分,从而消除因岩相变化造成的渗透率解释精度问题[8-9]。

南海西部油田乌石凹陷东区流沙港组三段具有较为丰富的旋转井壁心资料,对于岩相的地质雕刻具有重要意义。通过壁心的描述与薄片鉴定、激光粒度分析等实验手段相结合,对壁心岩性进行精确定相,提取关键测井曲线信息,建立岩相判识的样本集,采用Bayes岩性判别方法[10-11],建立岩相判别方程,对单井岩相进行数字划分,确定单井纵向上的岩相类型。为避免岩相划分过细造成岩相判别困难,将流沙港组三段岩相划分为4类:砂砾岩相(石英砾石含量大于50%);含砾粗砂岩相(石英砾石含量小于50%,粒度主要为粗粒);含砾中细砂岩相(石英砾石含量小于50%,粒度主要为中到细粒);细粉砂岩相(不含砾,岩性较纯的细粒岩性)。式(1)～式(4)是流沙港组三段选用自然伽马(GR)、深侧向电阻率(RIld)、中子(CNL)和密度(DEN)这4项参数利用Bayes岩性判别法建立的岩相判别方程。岩相判别共选取岩心和壁心上典型的30个岩相样本(砂砾岩岩相9个、含砾粗砂岩岩相6个、含砾中细砂岩岩相9个、细粉砂岩相6个),共判识错误3个,样本的回判率为9%,与实际取心和壁心岩相类型吻合率高,可以用于流沙港组三段砂砾岩储层的岩相精细划分。

砂砾岩相判别方程

S1=-3807.805+4.633GR+61.993RIld+

31.234CNL+2770.032DEN

(1)

含砾粗砂岩相判别方程

S2=-3884.086+4.807GR+62.932RIld+

31.078CNL+2797.297DEN

(2)

含砾中细砂岩相判别方程

S3=-4042.151+5.467GR+67.621RIld+

31.784CNL+2828.173DEN

(3)

细粉砂岩相判别方程

S4=-4298.132+5.981GR+71.774RIld+

32.454CNL+2900.662DEN

(4)

2.2 孔隙结构参数测井定量表征

(1)孔隙结构参数与物性。沉积作用、成岩作用决定了储层孔隙结构和空间配置,体现在孔隙喉道半径、孔喉的迂曲程度和有效孔隙空间配置上,微观孔隙结构从根本上影响了储层的渗透率。从排驱压力、孔喉半径平均值等孔隙结构参数与储层物性的关系可以看出(见图1),储层渗透率与排驱压力呈明显的负相关,储层渗透率与孔喉半径呈明显的正相关,相关程度较高,说明喉道对储层渗透率影响程度较高。

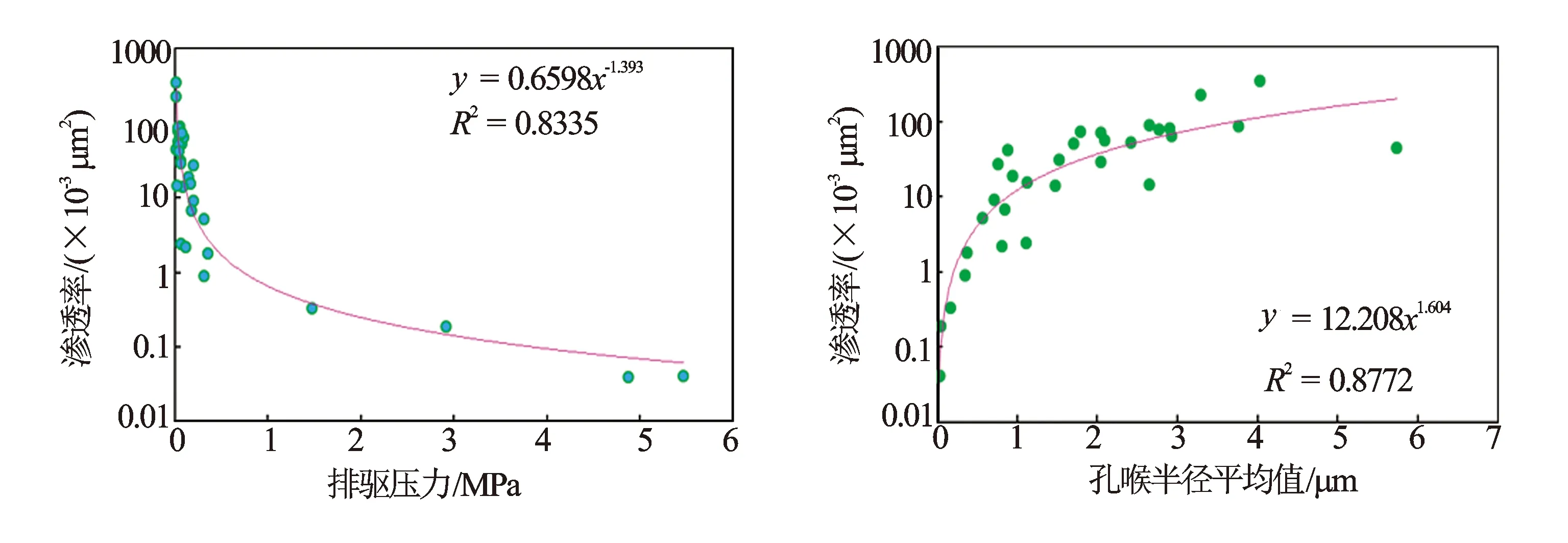
图1 乌石东区流沙港组三段排驱压力、孔喉半径平均值与渗透率的关系

(2)储层品质指数分级下的孔隙度渗透率关系。表征储层微观孔隙结构的参数很多,但是这些参数大部分属于微观参数,可依靠取样测试分析求得,但直接求取则很困难。因此,需要一个与储层微观孔隙结构相关的宏观参数,作为储层孔隙结构参数与测井信息之间的纽带,实现储层孔隙结构参数及储层渗透率的测井评价。通过调研砂砾岩储层及低渗砂岩储层相关文献,选用储层品质指数作为评价储层微观孔隙结构的中间桥梁[12],以期确立渗透率、孔隙度与孔隙结构参数之间的相关关系。

储层品质指数定义:假设单位体积岩石样品的孔隙由n个半径为r的毛细管组成,则储层品质指数

(5)

式中,Fs为形状因子,无量纲;τ为毛细管弯曲度,无量纲;K为渗透率,(×10-3μm2);φe为有效孔隙度,%。

从式(5)可见,宏观尺度上,Irq与储层的孔隙度和渗透率有关;微观孔隙结构来看,当毛细管变细(r减小)或弯曲度(τ)变大时,Irq均减小。因此,Irq与岩石的孔隙结构、孔隙度和渗透率均有关,是岩石微观和宏观物性特征的综合反映。

利用取心井段岩心物性分析数据计算储层的Irq,通过对储层品质指数聚类分级:Irq<0.8主要对应中孔隙度特低渗透率储层;0.81.5主要对应中孔隙度中渗透率储层。通过对储层品质指数与储层分类的对比分级,可见储层的孔隙度与渗透率的相关关系非常明显(见图2)。这反映了不同储层品质的孔隙度渗透率关系存在很大差异,靠单一的孔隙度渗透率关系,渗透率难以获得准确的解释结果。因此,储层品质指数参数可以作为储层孔隙度、渗透率与孔隙结构特征参数相互转换验证求取的中间桥梁。

2.3 多矿物模型孔隙度确定

孔隙度的精确求取是储层渗透率解释的关键因素之一,由于扇三角洲的沉积环境导致岩性、粒度、泥质和孔隙结构等都发生急剧变化,因此,孔隙度的确定需要从沉积的角度来确定模型。基于矿物分析和铸体薄片资料,流沙港组三段砂砾岩储层岩石骨架由砂岩和石英砾石组成,可利用这2种骨架加黏土和孔隙作为多矿物解释模型。根据上述模型分析,采用密度、中子和自然伽马建立测井响应方程。

(6)

方程组在求解时,结合区域地质特征,限定约束条件:0≤Vi≤1,i=1,2,3(1表示砂岩,2表示石英砾石,3表示黏土),0≤φ≤1。各组成分的测井响应值通过岩心分析资料确定,从而建立测井参数数据集,采用所建立的测井方程对流沙港组三段的测井资料进行处理,求取储层孔隙度。流沙港组三段70块岩心壁心实验分析的孔隙度与采用多矿物模型确定的孔隙度相关系数为0.893 7,平均相对误差为0.4%,误差率控制在7%以内,满足开发生产需要。

2.4 孔隙结构参数的测井表征

孔隙和喉道是碎屑岩储层孔隙结构的重要组成部分,影响着地下油气的储集和油气田的开发效果,是较为重要的地质描述参数[13-14]。储层岩石的孔隙结构参数可分为微观和宏观参数:宏观参数主要指储层的孔隙度和渗透率;微观参数主要描述岩石的微观孔隙结构,具体可以分为控制流体运动的微观特征参数、表征孔喉连通性的微观特征参数、孔喉的分选性、孔喉大小及分布等。这些参数的求取主要通过室内铸体薄片、CT扫描、扫描电镜、压汞等实验获得,资料往往存在局限性,很难推广。为此,前人基于大量的分析化验数据和特殊实验手段,通过测井资料求取这类微观孔隙结构参数。

国内外建立的低渗透率岩石微观结构模型较多,如毛细管束、分形理论、喉腔、格子气自动机和简化电导等模型,不同的岩石微观结构模型适用于不同的岩石孔隙结构。在对流沙港组三段储层岩心薄片和孔隙结构特征分析的基础上,通过类比分析,选用刘向君教授所建立的复杂低渗透率储层(致密低渗和复杂岩性储层)岩石导电模型,该模型结合复杂低渗透率地层孔喉细小且喉道多为片状的特点,选取毛细管束模型来模拟复杂低渗透率储层的导电规律。通过岩石导电实验推导出以下3个重要的微观孔隙结构参数模型[15]。

毛细管平均半径(rca)

(7)

孔喉迂曲度(τ)

(8)

孔隙结构指数(P)

(9)

式中,Rw为地层水电阻率;Sw为地层的含水饱和度;φ为地层孔隙度。

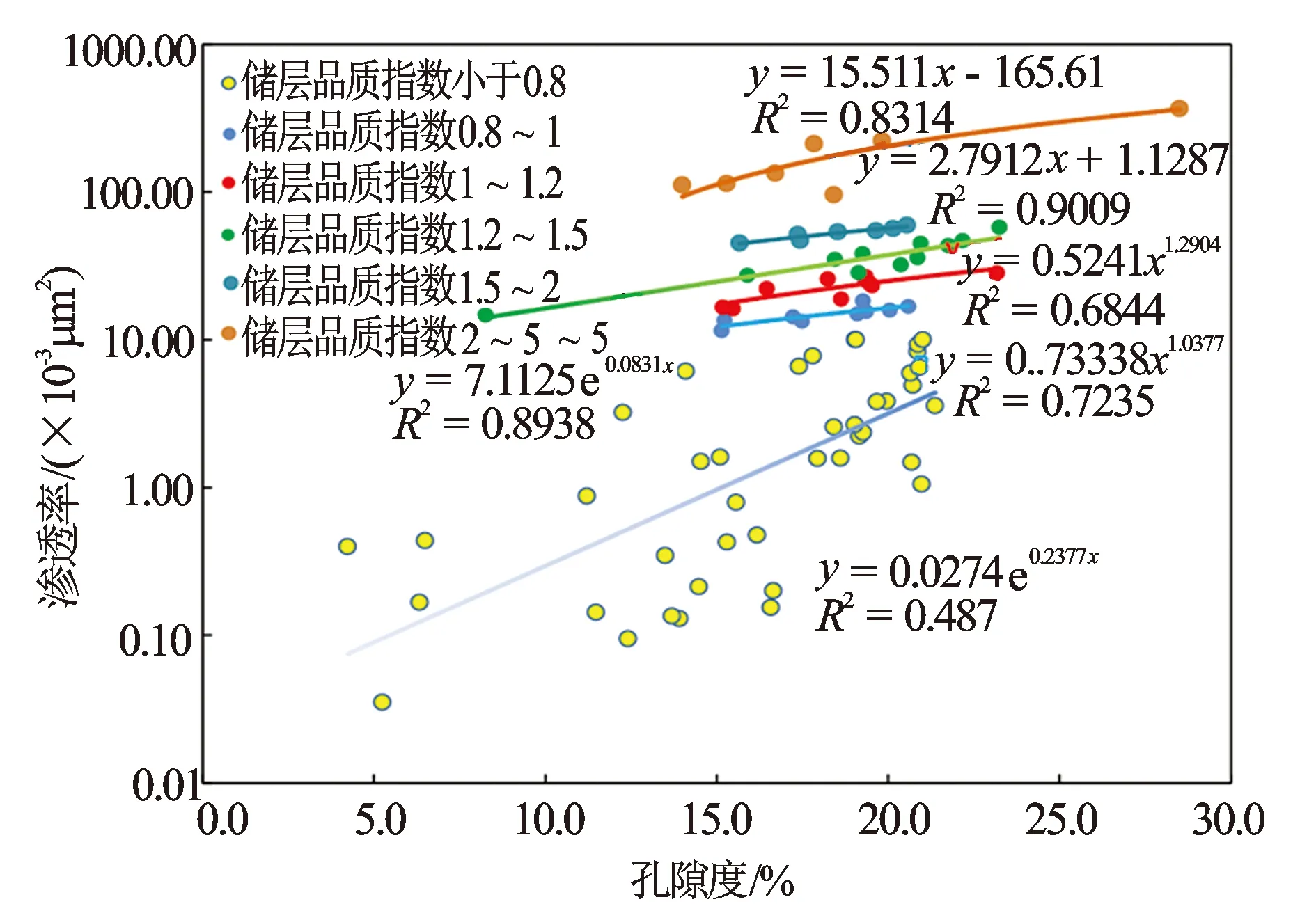
图2 乌石东区流沙港组三段储层品质指数分级下的孔隙度渗透率关系图

从式(7)、式(8)可见,当地层岩性和饱和流体的性质相似时,随电阻Rt变大,岩石的孔喉半径rca会逐渐变小,而毛细管的迂曲程度τ越大,反映储层孔隙结构变得越复杂。因此,可以看出地层电阻率Rt的纵向变化可以反映储层孔隙结构的变化。

孔喉半径rca、毛细管迂曲程度τ和孔隙结构指数P这3个孔隙结构特征参数可以较好地反映储层的孔隙结构特征。其中孔喉半径rca主要反映岩石孔隙喉道的平均大小;毛细管的迂曲程度τ主要反映岩石孔喉的曲折复杂程度;孔隙结构综合指数P是孔喉大小和孔喉曲折度的综合程度。因此,利用这3个基本参数可以较好地评价储层的孔隙结构特征,反映储集性能,也可以评价储层的渗透能力。通过对现有的流沙港组三段分析化验资料结合测井计算获得的孔喉半径、毛细管迂曲度和孔隙结构指数与储层品质指数之间存在较为明显的相关关系(见图3)。孔喉迂曲度增大,储层品质指数变小;毛细管平均半径越大,储层品质指数越大;孔隙结构综合指数越大,储层品质指数也越大。利用这3个参数实现储层渗透率的求取。

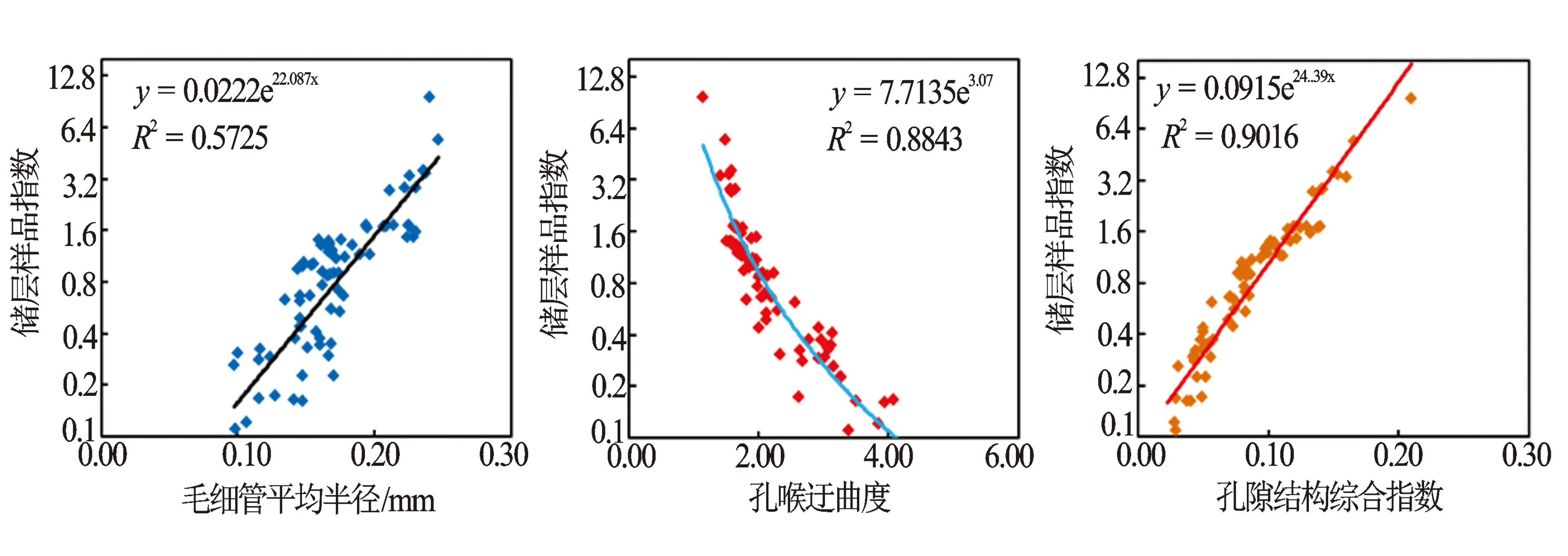
图3 毛细管平均半径、孔喉迂曲度和孔隙结构综合指数与储层品质指数的关系

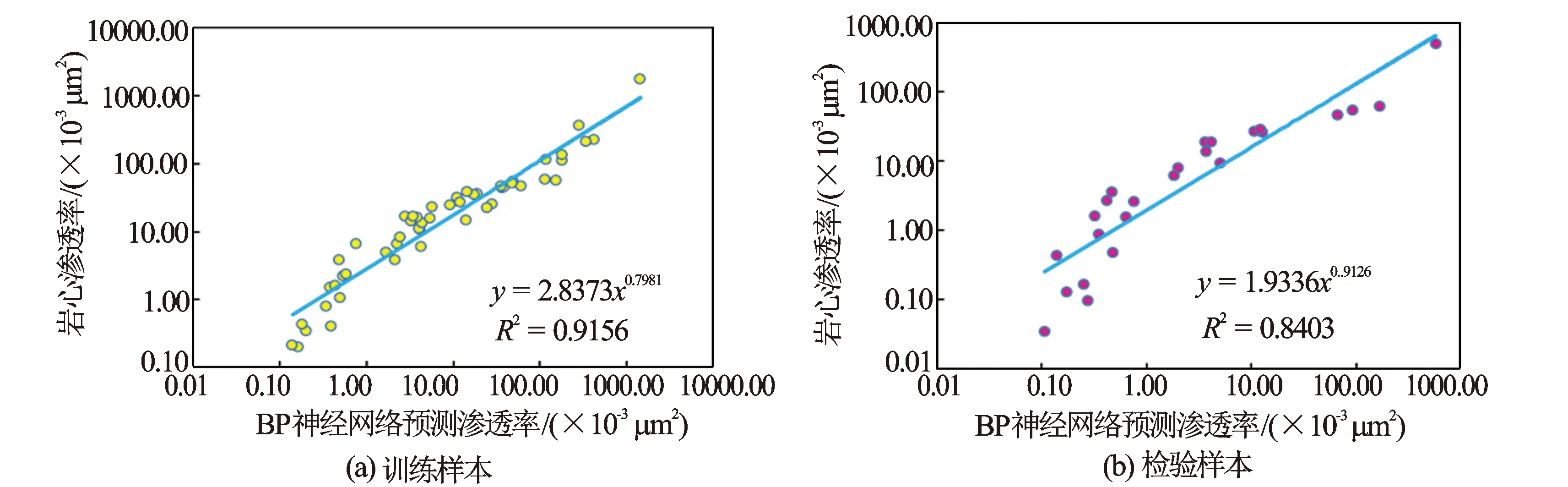
图4 乌石东区流沙港组三段BP网络法解释的储层渗透率与岩心渗透率对比图

2.5 渗透率精细解释

储层品质指数的测井表征参数建立后,尝试多种数学地质方法对储层渗透率进行解释,经过多次试验,最终选用阻尼最小二乘算法BP神经网络渗透率测井实现。

BP网络的算法基本原理是基于最速下降法的优化方法,属于最优化计算法中较为普遍但效率极低算法。结合流沙港组三段砂砾岩储层特征,考虑其因沉积、成岩作用导致的岩性复杂程度和孔隙结构的无规律性变化等因素,采用基于Levenberg-Marquardt算法(LM),即阻尼最小二乘算法原理,该方法是非线性最小二乘无约束优化的主要计算方法,其在地球物理和储层预测研究中已获得较好的效果[16-18]。

针对4类岩相分别设计BP神经网络结构,共3层:输入层、隐含层、输出层。经过反复试验,选取了岩石孔喉半径rca,毛细管迂曲度τ,以及孔隙结构指数P这3个测井孔隙结构表征参数组合,作为神经网络的输入层。输入结点为3个,根据隐含层结点个数大约为输入结点的2倍关系,隐含层选取6个结点,输出层取1个结点,这1个输出为特定岩相的储层品质指数的计算值,训练次数3 050次,误差精度为0.004 993时终止,解释效果最佳。利用该方法计算的特定岩相储层品质指数即可结合孔隙度反算出对应岩相的储层渗透率。

2.6 应用效果对比

带入训练的样本数53个,检验样本数25个,训练样本和检验样本通过储层品质指数反算的储层渗透率与岩心壁心试验分析的渗透率拟合效果均较好,表明该渗透率解释方法有效(见图4)。BP预测渗透率平均相对误差为56.91%,基本都控制在100%以内,解释结果在合理范围内。

乌石东区流沙港组三段属于低渗透率储层,不存在明显的宏观裂缝,储层的渗透率直接影响了单井的产能,测试产能与储层渗透性具有明显相关性,测试产能越大,试井渗透率和岩心的渗透率也越高。从WX-9井的处理结果与岩心实验求取结果对比来看,采用多矿物模型计算的储层孔隙度和基于孔隙结构采用BP神经网络计算的储层渗透率值大小和变化趋势均与实验求取值吻合性非常好(见图5)。动静态对比验证表明,基于孔隙结构求解的储层测井渗透率与岩心壁心渗透率和试井渗透率在数值和变化趋势上均具有明显的相关关系,相关系数分别为0.902 7和0.734 8。在其他取心资料井的检验对比也取得同样的效果,说明该解释方法是可行的,可以推广到全区应用。

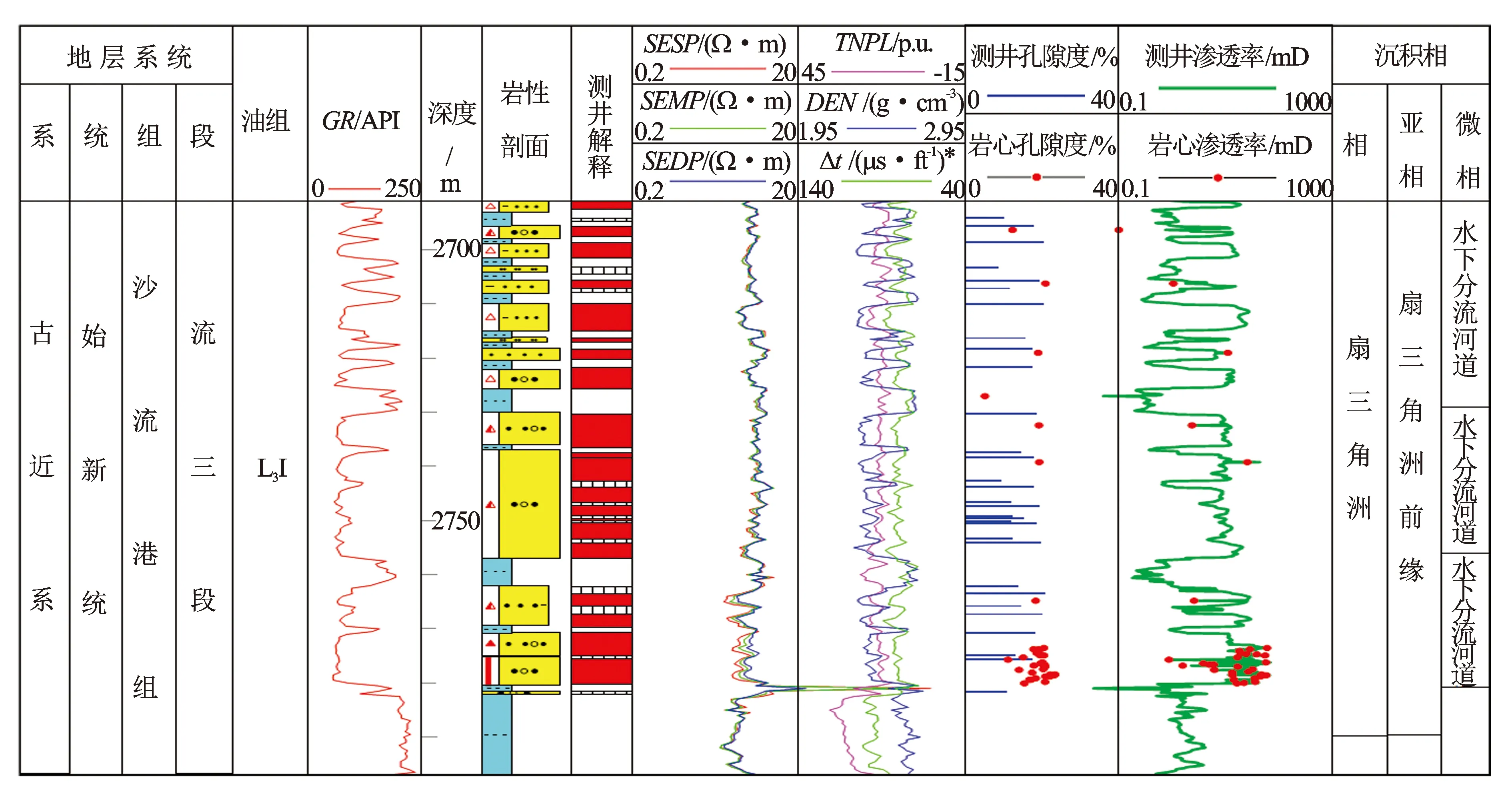
图5 乌石凹陷东区WX-9井综合测井解释与岩心、壁心实验测试结果对比剖面*非法定计量单位,1 ft=12 in=0.304 8 m,下同

3 结 论

(1)综合考虑流沙港组三段砂砾岩储层复杂的物性变化建立的基于Bayes判别原理的岩相判别方程,实现了利用测井资料在纵向上对岩相进行识别和精确划分。通过建立多矿物孔隙度计算模型求取满足精度要求的储层孔隙度,为储层渗透率的精细求解奠定了地质基础。

(2)引入储层品质指数这一中间桥梁实现孔隙结构特征参数的测井定量转换,采用非线性BP神经网络求取储层品质指数,进而反算砂砾岩储层渗透率,利用该方法求取的储层渗透率值大小和变化趋势均与实验求取值吻合性高,表明该解释方法可行,能够满足油藏地质综合描述和储量计算对参数的精度要求。