基于BF-PSO算法的水平井电阻率各向异性数值模拟与校正

张艺山,赵军,王英伟,李维,覃建华,张明玉

(1.北京大学地球与空间科学学院,北京100871;2.西南石油大学地球科学与技术学院,四川成都610500;3.中国石油新疆油田分公司研究院,新疆克拉玛依834000;4.中国石油新疆油田分公司,新疆克拉玛依834000)

0 引 言

电阻率能够很好地响应储层的流体性质,是测井评价储层含油饱和度的主要参数。利用测井仪器测得的电阻率值因受到井斜角、地层倾角、厚度及非均质性等因素的影响而失真,且在水平井中井斜角的影响尤为重要。研究表明电阻率具有各向异性,其实质是电阻率在地层中具有方向性[1-2]。倾角较小时,视电阻率主要受水平方向电阻率影响,随着倾角的增大,垂向电阻率作用逐渐增强[3-4]。随着计算科学的发展,电阻率数值模拟已成为解决电阻率各向异性问题的重要方法。利用三维有限元法,模拟电性各向异性倾斜沉积岩层的双侧向测井响应,为倾角校正提供理论基础[5-6]。在此基础上,建立倾斜地层各向异性正演模型,并利用多分量感应测井测定地层倾角,结合数值模拟结果提高地层评价的准确性[7];Jiefu Chen等[8]提出了一种用于电阻率测井快速模拟的三维有限元方法,有利于提高模型的精度;Song Hu等[9]利用三维有限元法模拟水平井地层模型的双感应和双侧向电阻率响应特性,为水平井测井解释提供了基础,并一定程度上提高了储层评价的准确度和可靠性。上述通过对电阻率的各向异性的正演研究,探讨了倾角对电阻率的影响规律,建立了不同地层倾角条件下的正演理论图版,但针对实测水平井井斜角影响的反演模拟及其校正方法仍然缺乏有效研究,因而不能有效地应用于实际水平井的测井解释评价中。

本文利用有限元方法,分析双侧向测井视电阻率在不同井斜角条件下的响应,结合基于粒子群算法的细菌觅食全局优化算法[10],建立了实测电阻率的反演算法。结合研究区地层平缓的单倾构造因素,考虑对水平井井斜角校正,对实际资料的处理实现了对实测电阻率井斜角影响的连续校正,有效地提高含油饱和度等参数的解释精度。

1 倾斜地层双侧向测井数值模拟

1.1 倾斜地层网格化物理模型

双侧向测井的数值模拟地层物理模型包括地层结构、上中下3层地层模型,具体表现为目的层的厚度h,井径D,电极系的位置坐标等;模型参数包括目的层电阻率Rt,地层相对介电常数ε,上下围岩的电阻率Rs,井眼内泥浆的电阻率Rf,地层电阻率各向异性λ。图1为模拟的地层模型(图1中紫色部分为目的层)。

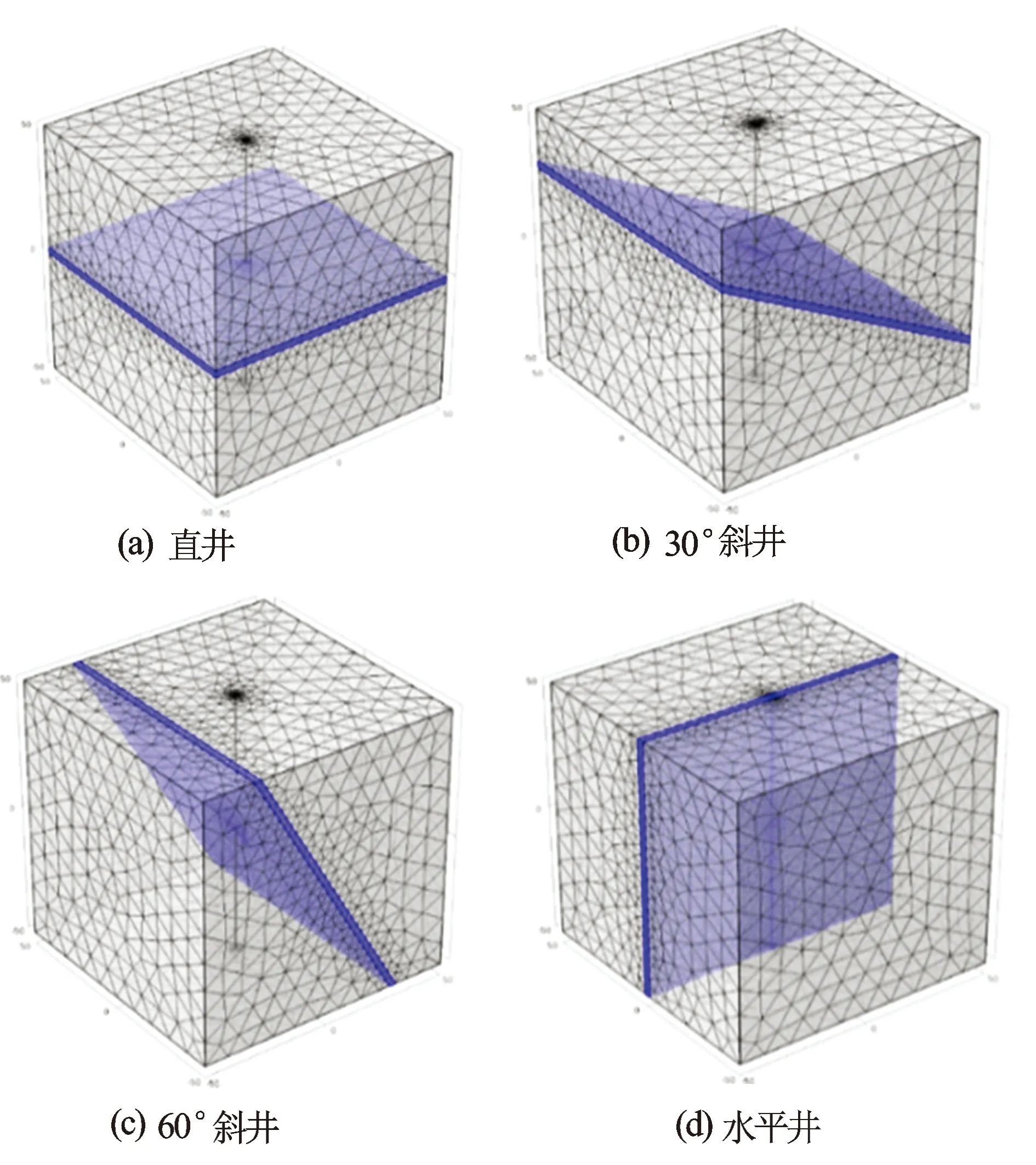
图1 4种倾角地层的网格划分模型

1.2 恒定电流场的有限元求解

有限元方法求解实际问题的步骤如图2所示。

图2 有限元方法计算流程

通过求解恒定电流场中电场及电流密度满足的麦克斯韦(Maxwell)方程

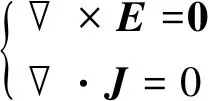
(1)

侧向测井确定电场中的电位分布,电位函数u(x,y,z)所满足的微分方程

(2)

求解过程中,地层应该满足以下4个边界条件。

(1)对于地层模型,在层的分界面上电位连续

u_=u+

(3)

(2)在层的交界面处电流是连续的

(4)

(3)整个区域边界上(无穷远处)电位为0

u=0

(5)

(4)双侧向仪器绝缘和整个区域边界上电流为0

(6)

利用有限元方法求解出电势分布,得到监督电极M1上的电势ΔU(M1)。由欧姆定律可知

(7)

式中,K为深、浅侧向测井仪器常量;ΔU(M1)为监督电极与回路电极的电位差,V;I0为主电极的电流强度,A。

2 数值模拟结果分析

2.1 模拟结果

考虑无泥浆侵入以及玛湖地区的实际地层条件,目的层电阻率大于围岩电阻率。地层模型参数:目的层厚度为2 m,目的层水平电阻率为100 Ω·m,上下围岩的电阻率为10 Ω·m,井眼内为盐水泥浆,井径为8 in(1)非法定计量单位,1 in=2.54 cm,下同,电阻率为0.1 Ω·m。深、浅侧向视电阻率随测量位置的变化见图3。

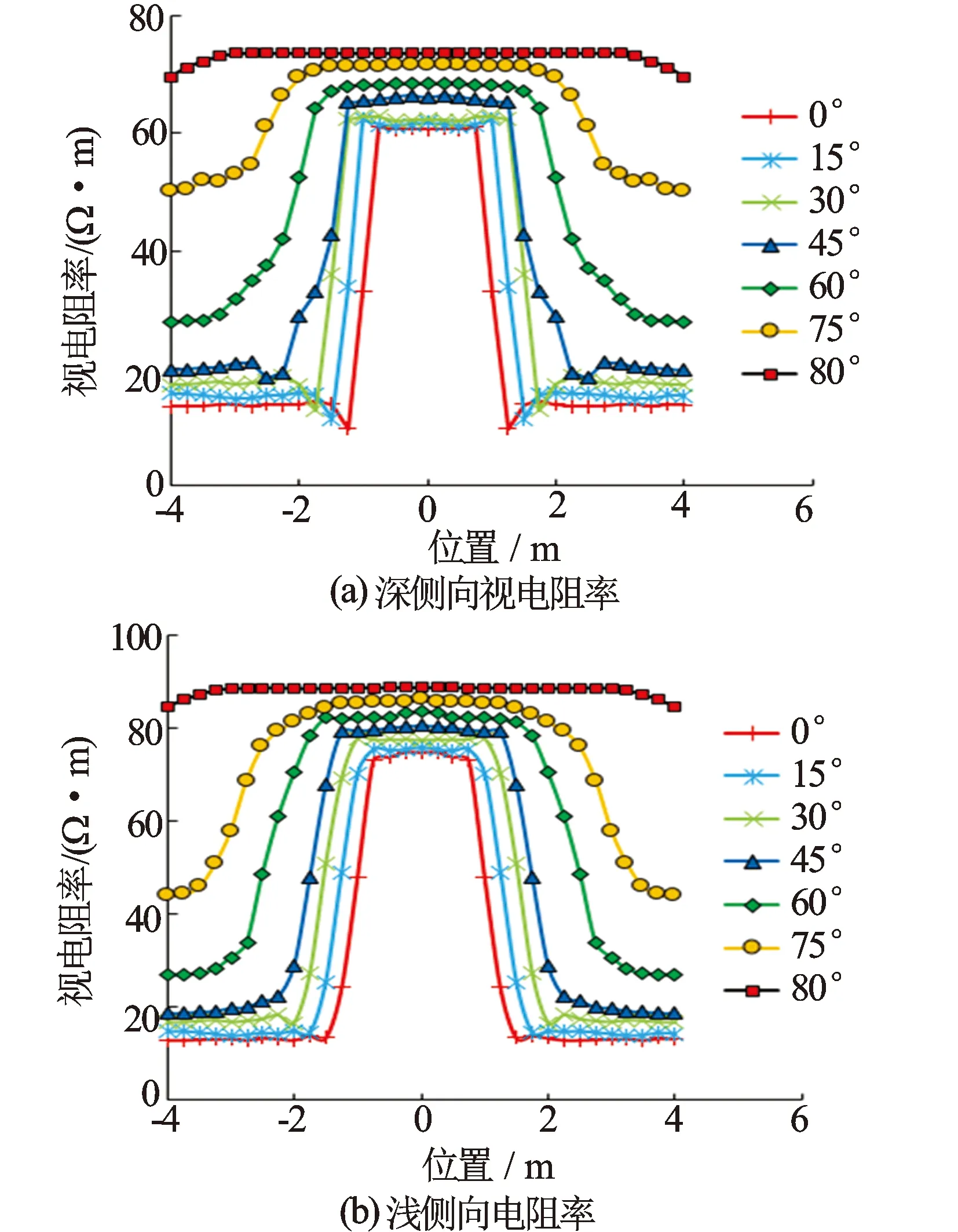
图3 不同倾角的双侧向电阻率测井响应特征

数值模拟结果表明,相同倾角条件下,深侧向视电阻率与浅侧向视电阻率存在一定差异,主要是由于深侧向探测深度较大,在目的层较薄的情况下,受上下围岩影响较大,而浅侧向探测深度较浅,受围岩影响较小;随着地层倾角增大,视电阻率在目的层的电阻率也增大,且增大的幅度逐渐减小,但其值始终低于目的层电阻率,这是由于低阻围岩的影响使得视电阻率达不到目的层电阻率;在不同倾角条件下,视电阻率在仪器位于目的层中心时,达到最大值,且随着井斜倾角的增大,视电阻率突变发生的离目的层中心距离增大;当井斜倾角接近90°时,视电阻率几乎不变,表现在图中近似为一直线。

2.2 校正方法

视电阻率受地层倾角、厚度及非均质性等因素的影响,在仅考虑倾角和电阻率各向异性的影响时,根据上述模拟结果,可建立关系图版(见图4)。图4表明,在相同的地层倾角情况下,ln (Rt/Rh)和ln (Rv/Rh)有较好的线性关系,且随着倾斜角度的增大,其斜率也随之增大。

采用非线性回归法,图版4可拟合为如下关系

0.428cosθ+0.030)R=0.996

(8)

式中,Rt为双侧向测井视电阻率,Ω·m;Rh为地层水平电阻率,Ω·m;Rv为地层垂向电阻率,Ω·m;θ为地层倾角,rad。

在实际测井资料中,由于很难准确获得地层垂向电阻率,故无法通过式(8)所给出的关系模型对电阻率进行倾角校正。为了解决这个问题,本文采用基于粒子群算法的细菌觅食优化算法对电阻率校正进行反演迭代求解。

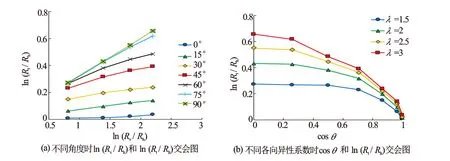
图4 电阻率和倾角、各向异性的关系示意图

2.3 反演算法

粒子群算法(PSO)是由Kennedy J和Eberhart R[11]率先提出的,它具有收敛速度快等优势,但缺乏有效机制跳出局部极值,精度较低。由Kevin M Passino[12]提出的一种新的仿生优化算法——细菌觅食算法(BFOA),全局搜索能力强,却收敛速度慢。基于粒子群算法的细菌觅食优化算法(BF-PSO)利用PSO收敛速度快和BFOA全局并行搜索的优点,快速得出最优解。

BF-PSO算法的关键步骤为趋化操作,即利用粒子群算法给细菌的趋化操作提供方向性指引。按照粒子群算法公式更新细菌个体的局部极值和细菌群的全局极值,并实现每一个细菌的翻转和游动。对于经过一个趋化循环的细菌群体,对每个细菌按照适应度的累加和进行排序,淘汰掉适应值较差的半数细菌,从适应值较好的半数细菌中分裂出同样的细菌群,这批细菌继承母细菌的位置和特性。经过一个繁殖操作的循环后,细菌有可能走向局部极值。因此,对于每一个细菌按照一定的迁移概率进行迁移,为了保证算法的收敛,需设定一定的迁移细菌数目。

该方法的实质是通过模仿细菌觅食的方法,寻求满足式(8)的最优解,反演地层真实电阻率而达到校正的效果。通过计算求解出所有细菌的成本函数,确定细菌更新的位置函数

P(i,j+1)=P(i,j)+c(i)Delta(n,i)

(9)

所有细菌向最优位置游动

J(i,j+1)=func(P(i,j+1))

(10)

评估所有细菌中个体最佳位置和全局最佳位置,细菌速度更新公式为

vi+1=wvi+c1R1(Plbest-Pcurrent)+c2R2(Pgbest-Pcurrent)

(11)

计算每个细菌的健康值并排序

(12)

终止条件为

i≥Nedori≤S

(13)

式中,P(i,j+1)为更新的位置函数;P(i,j)为当前位置函数;Delta(n,i)为利用PSO产生的随机向量;J(i,j+1)为当前最优解;Plbest为每一个细菌的历史最优;Pgbest为所有细菌的全局最优;vi为细菌的当前速度;R1、R2为0～1之间的一个随机数;Pcurrent为细菌的当前位置;w为惯性权重;n为搜索空间的维数;Nc为趋向操作数;Ns为游动最大步长;Nre为复制操作数;Ned为迁徙操作数;Pde为迁徙的概率;S为细菌总数。

3 资料处理

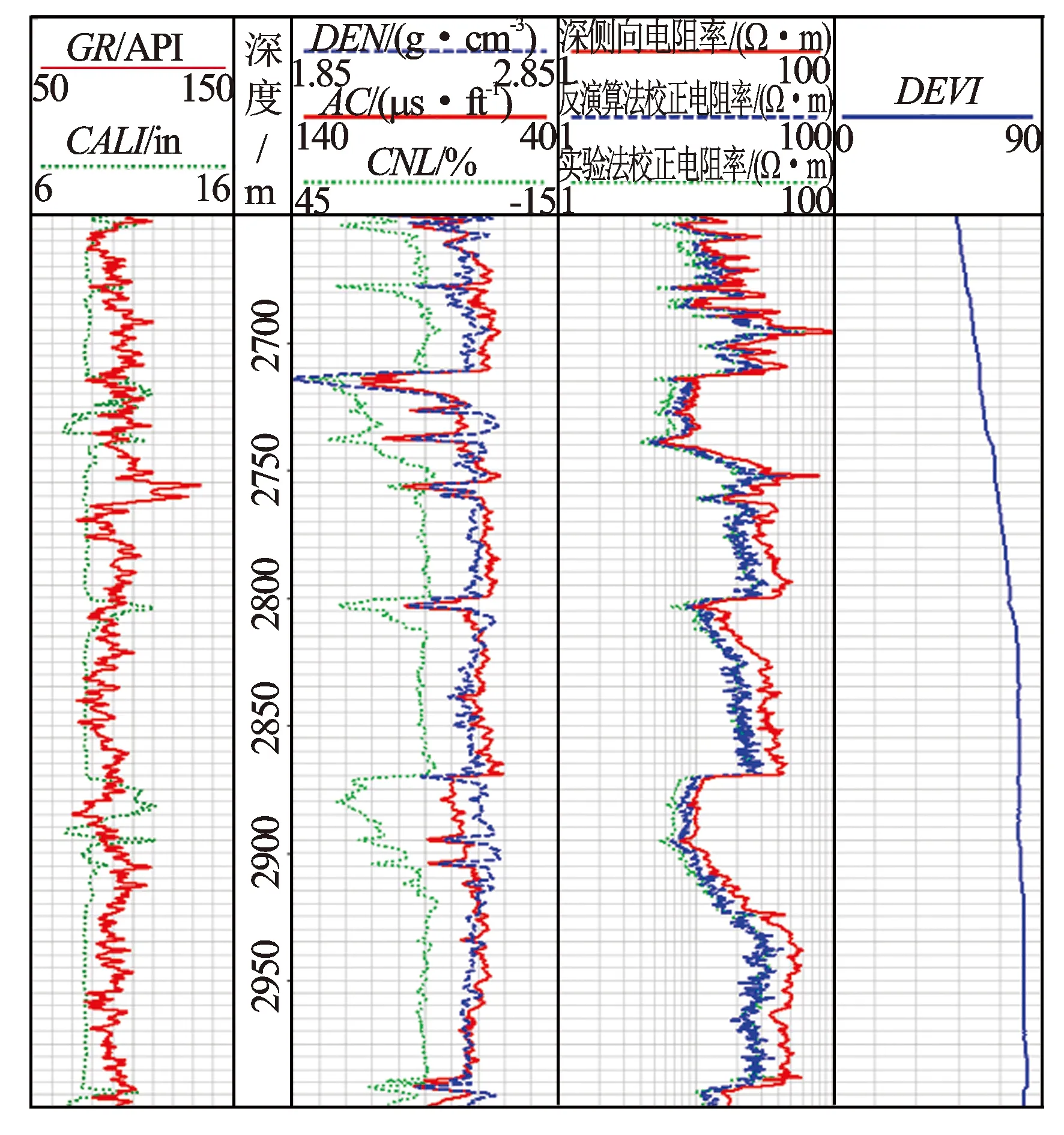
图5 水平井A井斜角校正结果

利用上述方法,对准葛尔盆地玛湖地区的水平井A进行井斜角校正。该井位于东南倾的平缓单斜构造带,地层倾角相对较小,因而只需对井斜角进行校正。对A井的井斜角校正结果见图5。从图5可见,各测井曲线质量良好。图5中的第3道为校正前后的电阻率曲线,在井斜角较大的层段,2条曲线的差异较明显,倾角越大,差异越明显,且视电阻率均大于校正后的地层电阻率。校正后的电阻率与玛湖地区岩心实测数据建立的校正结果相关性较好,两者误差小于5%。

利用校正后的电阻率对水平井B的含油饱和度等参数重解释,并将校正前后的电阻率曲线解释结果与试油结论进行对比(见图6)。图6中电阻率道显示了校正前后的电阻率值,第5道显示了校正前后计算的含油饱和度。在3 963～4 057 m井段原解释结论为油层,解释的含油饱和度较大,校正后的结论为油水同层,试油结论显示该水平段为油水同层,说明经校正后的电阻率判别的储层流体性质与试油结论吻合度更好。

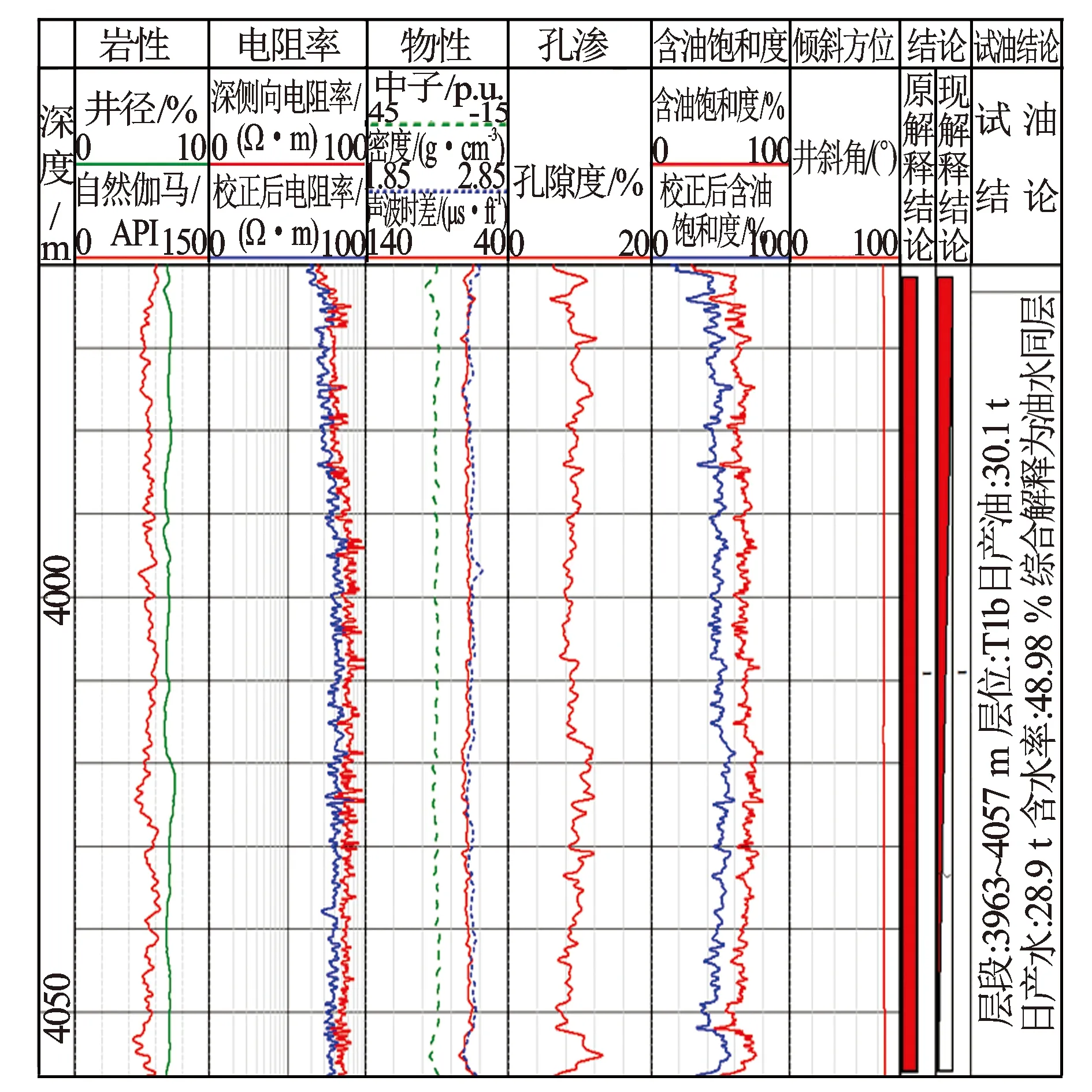
图6 水平井B井斜角校正结果

4 结论与认识

(1)采用有限元数值模拟,结合BF-PSO算法反演地层水平电阻率,可有效地消除水平井中井斜角对测井电阻率的影响。

(2)模拟结果表明,随着井斜角的增大,目的层视电阻率与地层真电阻率的差异越大,深、浅侧向电阻率受地层非均质性的影响也越大;当地层垂直电阻率大于水平电阻率时,目的层测井视电阻率大于真实电阻率。

(3)采用BF-PSO反演算法结合正演模型,实现水平井测井视电阻率的井斜角连续校正,消除了地层电阻率各向异性的影响,而通过校正后电阻率曲线能够很好地反映地层含油饱和度等参数,提高水平井解释的精度。