行为保险学系列(二十八):记忆存量决定风险判断偏差:综合直接经历与间接经验
郭振华 上海对外经贸大学金融学院
除依赖自身经历来感知风险之外,个体还通过观察自己周边他人遭受的风险事件来评估自己面临的同类风险的大小,也就是说,间接经验(曾经观察到的他人遭受的风险事件)也会对自己的风险判断造成一定的影响。例如,多数人有这样的感觉,看到亲戚朋友生病住院做手术,心里就有些打鼓,生怕自己也会经受同样的疾病和手术。这种影响既是人们的直觉反映,也是理性的表现。风险发生的统计概率,就是依据对大量人群出事频率进行统计的计算结果,其内在的假定是:对于相同种类的风险,每个人都有相同的出险概率。这一假定反映了理性人对他人遭受的风险事件会感同身受。
我们在本系列上一篇《记忆存量决定风险判断偏差:仅考虑直接经历》中,已经对个体依据直接经历形成的记忆存量进行风险判断作了系统分析,本文再加进个人的间接经验,分析直接经历和间接经验对风险判断偏差的综合影响。
一、间接经验对风险判断的影响
间接经验包括两种,一种是观察到别人遭遇风险,另一种是观察到别人未遭遇风险,这两种间接经验都会对个体的风险判断造成影响。
(一)观察到他人遭遇风险对个体风险判断的影响
个体观察到的风险事件即间接经验,来源包括亲眼所见的风险事件和从媒体上看到的风险事件,亲眼所见的风险事件通常是发生在亲朋好友身上,或是在路上巧遇的风险事件。上述观察到的风险事件都会存在个体的记忆中,进而对其未来风险判断造成影响。但是,从影响程度来看,媒体上看到的和路上巧遇的风险事件,可能过一段时间就忘掉了,不会形成长久记忆,对未来风险判断影响很小;而那些观察到的发生在亲朋好友身上的风险事件,个体受到的刺激或负面体验感往往很大,很可能长久地留在人们的记忆中,对其未来风险判断造成较大影响。
例如,目睹亲朋好友的房子着火和在报纸上看到某遥远地区的与自己毫无关联的房子着火,对个体主观火灾概率的判断,前者的影响要大得多,主观概率更大。诺贝尔奖得主圣捷尔吉(因“与生物燃烧过程有关的发现,特别是关于维生素C和延胡索酸的催化作用”而获得1937年诺贝尔生理学或医学奖)曾说过:“如果我看到一个人正遭受苦难,我会被深深打动,并甘愿冒生命危险去救助他。但接下来,我却能够不带感情地谈论大城市可能的毁灭以及随之而来的100万人的死亡。”
也就是说,间接经验对风险判断的影响程度受到“情感距离”的影响。所谓情感距离,是指观察到的风险事件受害者与自己(风险判断者)的情感紧密程度,情感越紧密,情感距离越小。通常,情感距离越小,观察到的风险事件例证对自己的风险判断影响越大,越容易引发风险高估。或者说,间接经验对个体风险判断的影响会随着情感距离的增大而衰减。那么,衰减速度如何变化呢?如果是直系亲属遭遇灾难,个体会显著地高估风险;如果是一般同事遭遇灾难,个体感知到的风险就相对较小;如果是遥远的与自己不相干的人遭遇灾难,个体感受不到风险的存在。也就是说,随着情感距离增大,个体的感知风险会迅速降低,情感距离过大,个体的感知风险几乎为零。感知概率随情感距离的变化曲线如图1所示。
图1中,在分界点,感知概率等于客观概率;在分界点左侧,感知概率大于客观概率,表示情感距离很近的人群会高估风险;在分界点右侧,由于情感距离较远,人们会普遍低估风险;当情感距离很大时,人们几乎感受不到这一风险的存在,感知概率为零。
(二)观察到他人未遭遇风险对个体风险判断的影响
观察到他人未遭遇风险对个体风险判断的影响机理,与上述观察到他人遭遇风险对个体风险判断的影响机理类似。即,看到他人未遭遇某种风险事故,已经遭遇风险的个体会调低自己的感知概率,未遭遇风险的个体则更加确信自己也不会遭遇同样的风险事故。只不过,这种感受和影响是在潜移默化中完成的,个体甚至都感受不到。而且,个体受到的上述影响大小也与情感距离成反比,情感距离越小,受到的影响就越大。
二、直接经历与间接经验的综合效应
(一)客观概率不变,加进间接经验的效果
对有损经验人群来说,首先,仅考虑直接经验时会高估小概率风险的出险概率;其次,小概率风险的间接经验,绝大多数都是他人未发生风险事件的信息,因此,间接经验会降低其感知概率。但是,由于间接经验的影响受到情感距离的约束,不是所有他人的风险信息都会对其造成影响,而且影响程度会随着情感距离的增大而迅速衰减。因此,在直接经历基础上增加间接经验,有损经验人群的感知概率会降低,但不会降低到客观概率那样低的程度,有损经验人群仍然会高估概率。
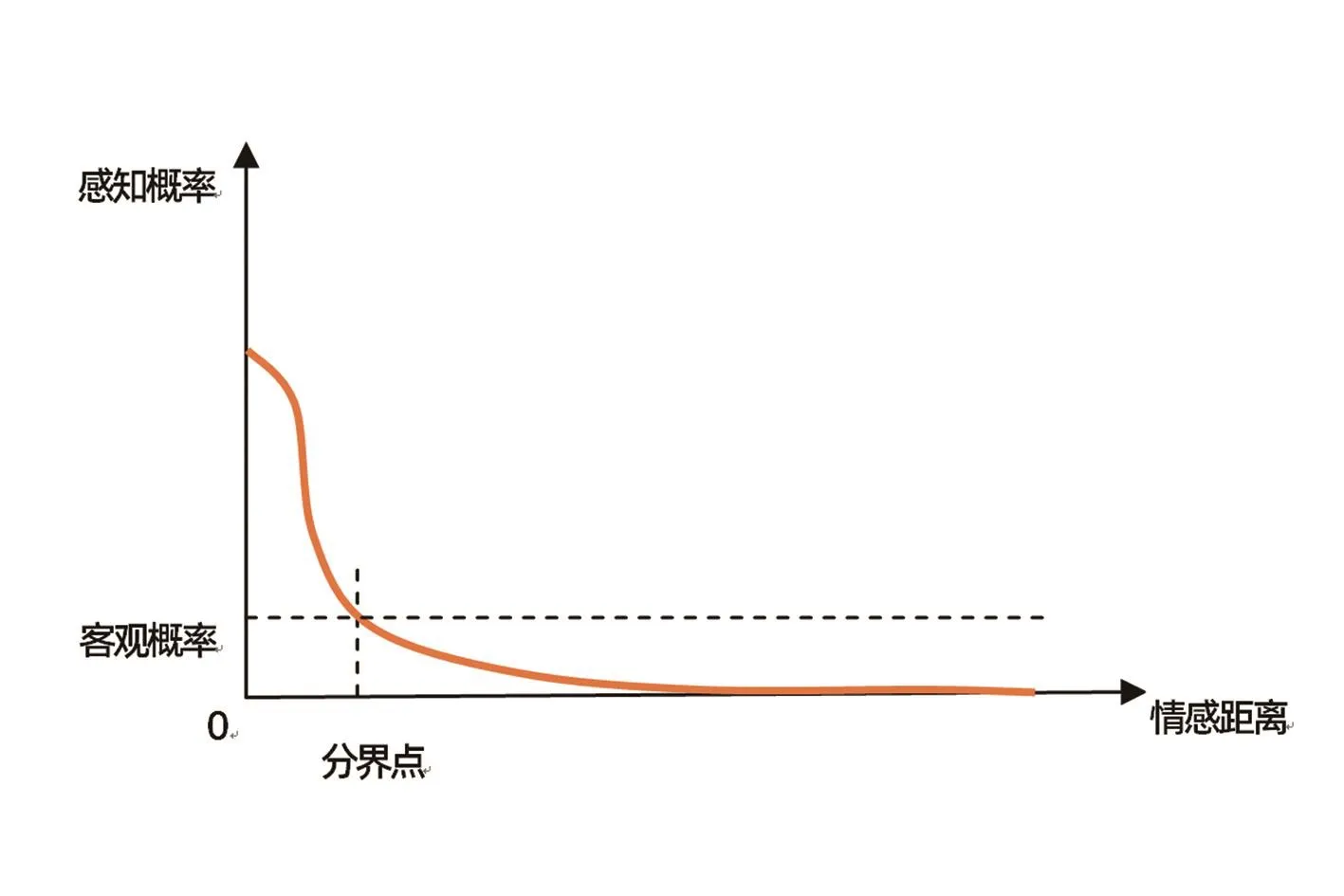
▶图1 情感距离对风险判断的影响
对无损经验人群来说,首先,仅考虑直接经验时会低估小概率风险的出险概率;其次,对小概率风险进一步考虑间接经验后,间接经验会增加风险事件记忆的可得性或可提取性,提升人们的风险感知。但是,由于风险事件发生的随机性,且其影响范围受到情感距离的限制,其影响是严重不平均的。可以将所有人想象为一个湖泊的水平面,随机发生的风险事件带来的影响,像是水平面上被少量投进的石子泛起的涟漪。由于石子数量较少(小概率事件),涟漪波及范围有限,导致只有少数人的感知概率会提升,其提升幅度取决于与石子投入点的距离。由此推断,对于小概率风险,间接经验将使无损经验人群中部分人群的感知概率有所提升,感知概率有所提升的人数占比,随着客观概率的增大而增大;感知概率提升幅度则取决于情感距离,情感距离越近,提升幅度越大。
最终,对出险概率为P的小概率风险而言,在综合考虑直接经历和间接经验后,与仅考虑直接经验相比,人们的风险判断偏差有所降低,但不会降低到与客观概率相等的程度。第一,有损经验人群的感知概率下降了一些,而有损经验人群通常就是高估概率人群,他们的高估倍数都会有所降低,但仍然高于客观概率。第二,无损经验人群的感知概率有所提升,受风险距离远近的影响,有的提高程度大(以至于从低估风险变为高估风险),有的提高程度小(以至于仍然低估风险),有的没有变化、仍然为零。而无损经验人群通常就是低估概率人群,因此,低估程度有所下降,他们的平均感知概率Pl从等于零变为大于零了,低估倍数P/Pl都会有所下降。第三,由于少数与遇险者情感距离很近的人会从低估风险变成高估风险,因此,高估风险者占比会有所增加,低估风险者占比会有所下降。
也就是说,与仅考虑直接经历相比,加入间接经验后,高估风险者占比有所增加且高估倍数有所降低,低估风险者占比有所下降且低估倍数也有所下降。
(二)客观概率变化带来的变化
根据《记忆存量决定风险判断偏差:仅考虑直接经历》中的相关数据,下面分析当客观概率为0.0002、0.05、0.1和1时,直接经历和间接经验对风险判断偏差的综合影响,进而概括出客观概率变化带来的风险判断偏差的变化规律。
当客观概率为0.0002时,仅考虑直接经历,99.88%的无损经验人群低估概率,感知概率为零,低估倍数为无穷大;0.12%的有损经验人群高估风险,感知概率为0.167,高估倍数为835。考虑间接经验后:第一,0.12%的有损经验人群,以及与其情感距离很近的原来低估风险的人,会变得高估风险,高估风险者占比略有扩大,若假定每个出险者会带动与其情感距离最近的2个人高估风险,则高估风险者占比增加至0.36%;第二,由于高估风险者的间接经验绝大多数都是不出险,以及部分低估者变成了高估者但高估程度较低,高估风险者的平均高估倍数(Ph/P)有所降低,但由于基数835倍很高,下降后仍然比较大;第三,高估风险者占比增加意味着低估风险者占比缩小,若高估风险者增加至0.36%,则低估风险者降至99.64%;第四,极少数与出险者情感距离较近的人群的感知概率有所上升,带动Pl有轻微上升,低估风险者的平均低估倍数(P/Pl)从无穷大有所降低,但由于加入间接经验后,大多数人仍然感受不到风险的存在,低估倍数较大。
当客观概率为0.05时,仅考虑直接经历,74.082%的无损经验人群低估概率,感知概率为零,低估倍数为无穷大;25.918%的有损经验人群高估概率,高估倍数为3.9。考虑间接经验后:第一,25.918%的有损经验人群以及与其情感距离很近的人会高估风险,高估风险者占比有所扩大,若假定每个出险者会带动与其情感距离最近的2个人高估风险,则高估风险者占比增加至77.754%;第二,由于高估风险者的间接经验多为不出险,以及部分低估者变成了高估者但高估程度较低,高估风险者的平均高估倍数(Ph/P)有所降低,高估倍数的基数为3.9,可能下降至2倍左右;第三,高估风险者占比增加意味着低估风险者占比缩小,若高估风险者增加至77.754%,则低估风险者降至22.246%;第四,由于客观概率0.05比较大,与出险者情感距离较近的人群占比也很大,意味着几乎所有未出险者的感知概率都会有所提升,带动Pl大幅上升,低估风险者的平均低估倍数(P/Pl)从无穷大大幅降低,低估倍数较小,但仍存在一定的低估。
当客观概率超过0.1后,仅考虑直接经历,54.881%的人低估,45.119%的高估。综合考虑直接经历和间接经验后,已经是随处可见出险者了,在任一个体情感距离较近范围内,其抽样误差大幅降低,风险判断准确程度大幅提升,低估概率者和高估概率者的判断都大幅逼近了客观概率,预计高估概率者占比和低估概率者占比也越来越接近(双方都接近50%),高估倍数和低估倍数都接近于1。
当客观概率为1时,不确定性消失了,人们都变得能够准确评估风险了,高估概率者占比和低估概率者占比均变为零。
综合上述分析,加进间接经验后,随着客观概率从零开始增长,相对于仅考虑直接经历,高估概率者占比迅速增加(高估概率者曲线相对于仅考虑直接经历更加向上倾斜),低估概率者占比迅速减少(低估概率者占比曲线相对于仅考虑直接经历更加向下倾斜)。客观概率超过0.1之后,人们的风险判断开始逐渐趋于理性,但仍然不是高估就是低估,只是高估概率者占比和低估概率者占比都逼近50%。当客观概率等于1时,人们变得能够准确评估风险,高估概率者占比和低估概率者占比均变为零。由此,低估概率者占比曲线和高估概率者占比曲线的大致规律如图2所示。
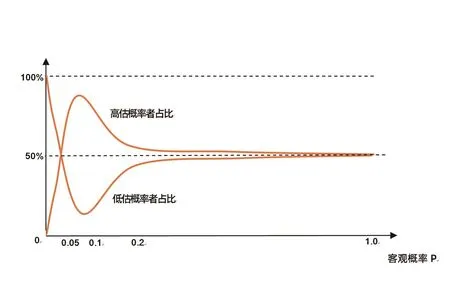
▶图2 高估(低估)概率者占比随客观概率的变化曲线

▶图3 高(低)估倍数随客观概率的变化曲线
同理,与仅考虑直接经历相比,考虑直接经历和间接经验的双重影响后,随着客观概率从0开始增长,平均低估倍数不再是无穷大了,平均高估倍数和平均低估倍数都会迅速降低。当客观概率超过0.1后,风险判断准确性大幅增加,平均高估倍数和平均低估倍数都迅速向1靠近。可以想象,当客观概率为1.0时,不确定性几乎消失了,风险事件的普遍发生形成普遍记忆,人们的感知概率与客观概率会完全一致,风险判断偏差消失了,高估倍数和低估倍数都等于1。由此,高估倍数和低估倍数的大致变化规律如图3所示。
三、结论和分析特色
(一)结论
对保险所承保的小概率风险而言,客观出险概率通常都低于0.2。因此,将图2、图3中客观概率大于0.2的部分截去,就得到了将直接经历和间接经验一并考虑后,人们的风险判断偏差规律,如图4、图5所示。
基本结论为:第一,人们不是高估风险,就是低估风险;第二,当客观概率很低时,低估概率者占比很大且低估倍数很大,高估概率者占比很小且高估倍数很大;第三,随着客观出险概率的增加,高估风险者占比迅速增加,低估风险者占比迅速降低,高估倍数和低估倍数迅速降低;第四,客观概率大致超过0.1后,高估概率者占比降低,低估概率者占比增加,双方都向50%逼近;第五,随着客观出险概率增加,低估风险人群的低估倍数和高估风险人群的高估倍数都越来越小。
(二)上述分析的特色
长期从事个体风险决策或保险决策的读者看到上述分析,多少会感到有些奇怪,因为上述分析给出了人群总体中的低估风险人群占比和低估程度、高估风险人群占比和高估程度,而不是个体的风险判断结果。
其实这正是行为保险经济学的优势所在。即,与标准保险经济学不同的是,行为保险经济学认为人们的风险判断结果不是同质的,或者说,对同样的风险,不是所有人都有一致的风险判断结果,而是有人高估有人低估。上述分析得到高估人群占比和高估程度、低估人群占比和低估程度,可用来进一步推导多少人保险需求旺盛、多少人需求疲弱,非常有利于分析保险市场的总体需求规律。
也就是说,行为保险经济学破除了标准保险经济学中的同质客观风险假设或风险评估一致性假设,用更加符合现实的异质主观风险来分析保险市场,可以得到更加符合现实的分析模式和结论。
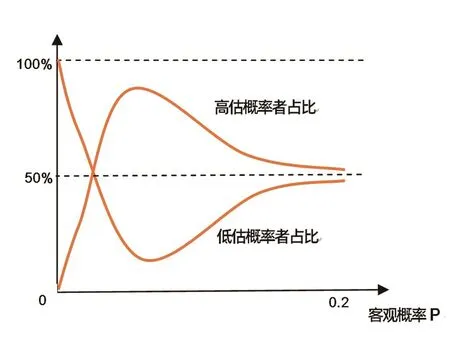
▶图4 高估(低估)概率者占比函数
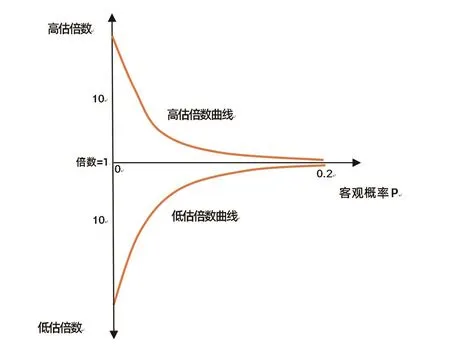
▶图5 高(低)估倍数函数

