完全二部图的超k-Steiner Wiener指数
乔晓云
(山西大学商务学院,山西 太原 030031)
0 引言
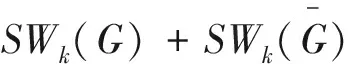
1 预备知识
定义1[6]二部图是指一个图,它的顶点集可以分解为两个非空子集X和Y,使得每条边都有一个端点在X中,另一个端点在Y中.完全二部图是指二部图中X的每个顶点都与Y的每个顶点相连.若|X|=m,|Y|=n,则这样的图记为Km,n.
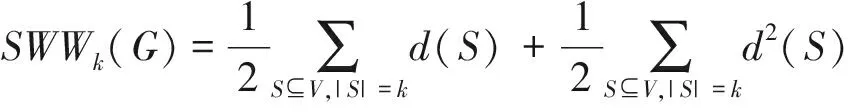
2 主要结论
定理:设G=Km,n(1≤m≤n)为完全二部图,2≤k≤m+n,则
证明 设G=Km,n(1≤m≤n)为完全二部图,V(Km,n)=U∪W,其中U={u1,u2,…,um},W={w1,w2,…,wn}.
(H1)当2≤k≤m时,对于∀S⊆V(G),|S|=k,则有以下三种情况S∩U=φ或者S∩W=φ或者S∩U≠φ,S∩W≠φ.
①对于S∩U=φ,则S⊆W.不失一般性,令S={w1,w2,…,wk},E′={u1w1,u1w2,…,u1wk},则G[E′]是包含S的Steiner树,则d(S)≤k.另一方面,由于G=Km,n是完全二部图,则包含S的任何树至少有k条边,即d(S)≥k.所以d(S)=k.
②对于S∩W=φ,同理可得d(S)=k.
③对于S∩U≠φ,S∩W≠φ,不失一般性,令S={u1,u2,…,ut,w1,w2,…,wk-t},E′={u1w1,w1u2,w1u3…,w1ut,u1wt,…,u1wk-t},则G[E′]是包含S的Steiner树,则d(S)≤k-1.另一方面,|S|=k,则连接S的任何树至少有k-1条边,即d(S)≥k-1.所以d(S)=k-1
由定义得
(H2)当m≤k≤n时,对于∀S⊆V(G),|S|=k,则有以下两种情况S∩U=φ或者或者S∩U≠φ,S∩W≠φ.根据(H1)的情况①③同理可得S∩U=φ时,d(S)=k.S∩U≠φ,S∩W≠φ时,d(S)=k-1.
由定义得
(H3)当n≤k≤m+n时,对于∀S⊆V(G),|S|=k,则S∩U≠φ,S∩W≠φ.根据(H1)的情况③同理可得.S∩U≠φ,S∩W≠φ时,d(S)=k-1.
由定义得
综上所述,定理得证.

