一种基于笔形束核的快速剂量计算方法

毛凯娜，张鹏程，桂志国

1.中北大学信息与通信工程学院，山西太原030051；2.生物医学成像与影像大数据山西省重点实验室（中北大学），山西太原030051

前言

恶性肿瘤己成为严重危害人类健康的一类疾病，目前治疗肿瘤的三大主要手段为放射治疗、手术治疗和化学药物治疗。与其它两种治疗方式相比，放射治疗能最大限度将照射剂量集中在靶区，在不同程度上保留被治疗器官的功能，改善患者的愈后生存质量，从而成为众多学者的研究重点。近年来随着放射物理学、计算机科学技术、医学影像技术等学科的更新与发展，出现了许多新的放疗技术，目前临床研究较为广泛的一项技术是调强放射治疗（IMRT）。在IMRT 中，逆向计划系统的方案优化过程中需要频繁计算射线在病人体内的剂量沉积，剂量计算的精度决定方案优化的质量，剂量计算的速度则影响方案优化的时间。因此，精确快速的剂量计算是放射治疗系统的核心。

近年来，剂量计算的研究重点是半解析法和解析法。解析法包括蒙特卡罗法［1］（Monte Carlo,MC）和求解粒子输运方程的方法［2］，虽然它们能够精确地模拟射线在病人体内的能量沉积过程，但是由于计算量复杂，还是无法满足方案优化对剂量计算速度的要求，因此很多肿瘤治疗系统仍然采用半解析法进行逆向计划系统的方案优化。常用的半解析法是基于核模型的剂量计算方法，包括笔形束核剂量计算方法［3］和点核剂量计算方法［4］，其中基于点核剂量计算方法的计算精度较高，但计算速度较慢；基于笔形束核的剂量计算方法虽然计算精度不高，但计算速度快，因此目前在临床上仍然被广泛使用和研究。1992年，Ahnesjö 等［3］提出一种指数函数表示的笔形束核模型，利用三角场积分将主要剂量与散射剂量分开计算。2006年和2007年，Whitton 等［5］和Zhou等［6］分别提出可编程门阵列（Field Programmable Gate Array,FPGA）的加速剂量计算方法，利用硬件实现剂量计算的加速。2008年，Tillikainen 等［7］提出在球壳坐标系下计算剂量分布的笔形束核模型，同时用6个指数函数表示笔形束核的侧向分量，增加剂量计算的精度。2010年，Lu［8］提出一种混合剂量计算方法，能够兼容笔形束核剂量计算速度和点核剂量计算精度，不过计算过程还是比较复杂。2011年，Chen 等［9］利用GPU 对点核剂量计算方法进行加速，但还是没有达到降低算法本身的计算复杂度的目的。

由于笔形束核剂量计算中，计算量最大的部分在于重复利用射线追踪法计算笔形束核侧向分量中轴线与体素的相交情况，因而减少射线追踪法的使用，降低轴线与体素相交的计算次数就可以降低算法复杂度。本文结合文献［7］方法，提出一种降低笔形束核剂量计算复杂度的算法。在球壳坐标系下，以碰撞点为中心计算剂量分布，每一层碰撞点处轴线与体素的相交情况都是一致的。因此每条射束只需计算初始层轴线与体素的相交情况，再根据体素的相对位置和校正因子得到其它层轴线与体素的相交情况。在这种情况下，轴线与体素相交次数的计算量减少，继而算法复杂度降低，计算速度也会大大提高。

1 获取核参数

1.1 球壳坐标系

本文使用的模拟照射源为点源。由于在直角坐标系中，点源发出的射线不是平行入射，因而传统算法根据发散射线的偏转角度，适当旋转中心轴处的笔形束核从而得到对应角度的笔形束核［10-11］。然而旋转笔形束核是非常耗时的方法。但是在球壳坐标系下［7］，来自点源的射线垂直于每一个球壳，仍然可以按照平行射束的方式计算剂量分布，避免对笔形束核的旋转，从而减少计算时间。

笔形束核的坐标系以正交基的形式给出。笔形束核按照固定顶角进行采样［7］。在这种采样方式下，由直角坐标系到球壳坐标系的映射关系表示为：

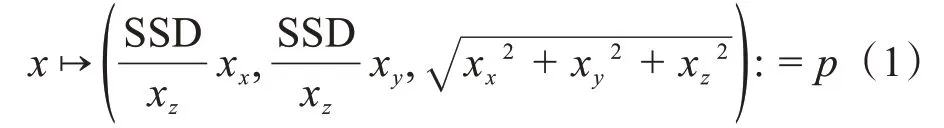
式中，x=(xx,xy,xz)表示直角坐标系中的点，p=(px,py,pz)表示在球壳坐标系中对应的点，:代表映射关系，从直角坐标系映射到球壳坐标系。

1.2 笔形束核参数的获取

通常将笔形束核分为两部分：深度方向分量和侧向分量。深度方向分量表示射束β在模体深度为pz的球壳层上释放的所有能量，均匀介质中的深度分量表示为：

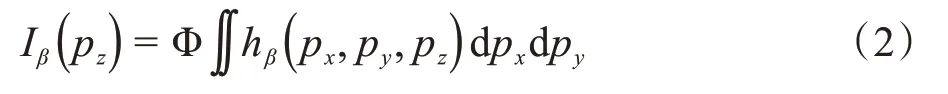
其中，Φ 表示模体表层的能量注量分布，hβ表示基于光束β的多能核［7］。

在非均匀介质中根据有效深度和相对电子密度［12］对深度分量进行校正：

其中，ρ(p')表示射束与模体在实际深度层碰撞点p'处的相对电子密度：

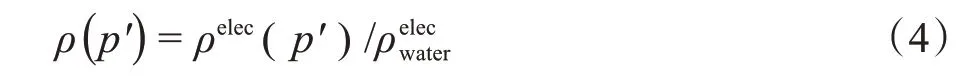
其中，pz'表示射束入射到模体内的等效深度，用d(X)表示：

其中，X为射束在模体内入射的实际路径。

侧向分量fβ(r,pz)表示在距离射束中心轴长度为r的体素中接收到的由该射束在深度为pz的球壳上释放的部分能量分量：

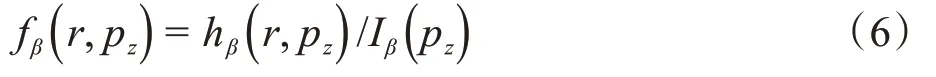
在本文中我们使用了由Tillikainen等［7］提出的侧向散射函数来模拟侧向分量：

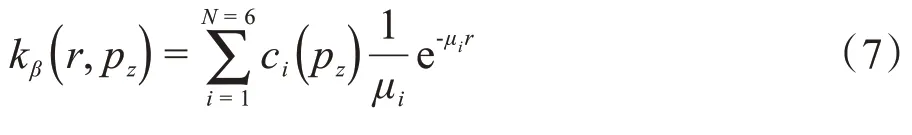
其中，μi是衰减因子，将在1 到200 mm 内按等对数间隔取值得到。ci(pz)是侧向散射函数的权重参数，通过对fβ(r,pz)和kβ(r,pz)进行最小二乘法拟合得到。r是碰撞点处轴线与体素相交的有效长度，通过射线追踪法计算得到。

在非均匀介质中，需要根据有效深度对应球壳层碰撞点处轴线与体素的相交长度以及沉积点的相对电子密度对侧向分量进行校正：

其中，ρ(p)是能量沉积点p处的相对电子密度。本文方法r值无需在有效深度下进行校正，可以直接通过初始球壳层轴线与体素的相交情况得到。下文会详细介绍。

最后将笔形束核中的深度分量Iβ(pz)、衰减因子μi、权重参数ci(pz)保存，为后续剂量计算的使用提供方便。

1.3 剂量计算

本文使用Ahnesjö等［4］提出的筒串卷积算法对笔形束核进行叠加来计算模体内各点处所有沉积的能量。同时使用等效路径［13］的方法来校正非均匀介质中的剂量分布。为了方便在计算机上实现，使用8个离散的筒串方向［7］进行能量叠加。射束β在模体内p点处沉积的能量表示为：

射野内所有射束在p点处沉积的总能量为：

其中，S为射野内所有射束的集合。

将单位质量中接收到的能量定义为剂量，因此在直角坐标系下x点处的剂量为：

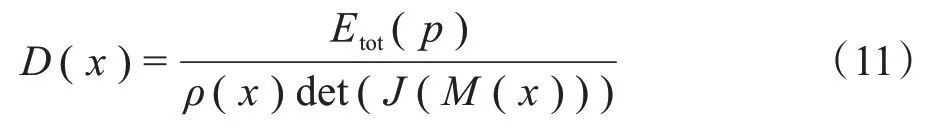
其中，J(M(x))是两坐标系之间映射关系M的雅克比行列式，雅克比行列式的值为：

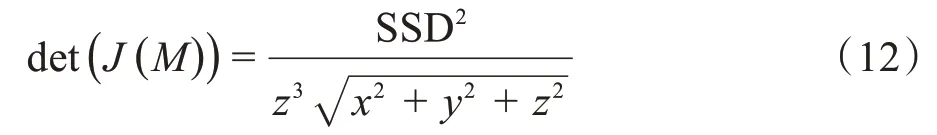
2 本文算法

2.1 算法改进部分

在笔形束核剂量计算方法中，射束进入模体之后的所有能量按笔形束核的概率分布模型进行沉积。在笔形束核侧向分量的校正中，传统的笔形束核剂量计算是以能量沉积点为中心计算剂量分布，该方法需要重复利用射线追踪法［14］计算射野内所有射束在不同方向上轴线与体素的相交长度，计算过程复杂，计算量较大，比较耗时。因而提出以碰撞点为中心计算剂量分布的改进方法，根据射束在不同层碰撞点处能量散射方式的相似性，通过只计算初始球壳层碰撞点处的不同方向轴线与体素的相交情况的方式来减少射线追踪的计算次数，进而减少计算量。

在球壳坐标系下，随着模体深度的增加，不同球壳层体素的实际体积在增大，轴线与体素的实际相交长度也相应增加。但是其它层碰撞点处轴线与体素的相交长度与初始层碰撞点处轴线与体素的相交长度的比值是一个与体素深度位置相关的值，将这个比值作为校正因子提前计算。本算法计算射束在初始球壳层碰撞点处的不同方向轴线与体素的相交情况并保存。然后在剂量计算中根据射束与球壳层碰撞点的位置计算出相对偏移位置，从而获得当前球壳层碰撞点处与轴线相交体素的密度值；同时利用校正因子，得到轴线与体素相交的有效长度。对于一条射束，该方法只计算了一层轴线与体素的相交情况，大大减少了射线追踪的计算次数，并且在最大射野面积下存储的一条射束8 个不同方向轴线与体素的相交比例的数据内存大小仅为0.2 M，减少计算过程中的大量内存方面的开销。

对于笔形束核剂量计算模型，在直角坐标系中将模体看做N=n×n×n个大小相等的立方体组成，每个立方体代表一个体素，将体素的中心点坐标(xx,xy,xz)作为体素的索引坐标。同时将模体中每个体素的密度定义在一个三维数组中。在计算时通过式（1）的变换将体素坐标对应到球壳坐标系中。利用射线追踪法计算初始层某一方向轴线与体素相交的有效长度为：

其中，ρs(px,py,pz0)表示与轴线相交的体素(px,py,pz0)的密度值，lengths(px,py,pz0)表示在初始层轴线与体素(px,py,pz0)的相交长度，n表示与轴线相交的体素个数。

在计算其它层轴线与体素的相交长度时，需要首先根据碰撞点的位置计算出相对偏移位置，获得待计算球壳层碰撞点处与轴线相交的各体素的密度值，然后利用校正因子，得到待计算球壳层对应方向轴线与体素相交的有效长度：

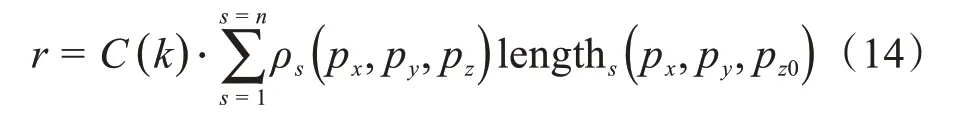
此处的ρs(px,py,pz)表示计算层与轴线相交的各体素的密度值。C(k)是与球壳深度有关的校正因子：

其中，pz表示待计算球壳层的深度，pz0表示初始球壳层的深度。

2.2 算法步骤

本文的算法设计流程如图1所示，算法步骤如下：（1）输入剂量计算所需的模体三维密度信息和射野信息。根据输入的数据信息，利用MC 方法精确模拟笔形束核［15］，对于同一个治疗头，只需生成一次核模型即可。（2）核参数计算与保存。拟合式（6）和式（7）获得衰减因子μi和权重参数ci( )pz，将笔形束核中的深度分量Iβ(pz)、衰减因子μi和权重参数ci(pz)存入查找表。在球壳坐标系下，计算笔形束核模型中每条射束在初始球壳层碰撞点处轴线与体素的相交情况以及校正因子并保存在数组中。对于一条射束，只需利用射线追踪法计算一次初始层碰撞点处不同方向轴线与体素的相交情况即可。（3）沿射束前进方向确定射束与体素发生碰撞的位置，根据该碰撞点的位置读取存储的笔形束核模型参数、体素密度信息和校正因子，计算在该碰撞点处各轴线与体素的相交长度，进而得到该碰撞点处的能量沉积。（4）将步骤（3）中得到的球壳坐标系下的能量分布转换为直角坐标系下的剂量分布，并与传统算法和MC算法进行比较得出结果。

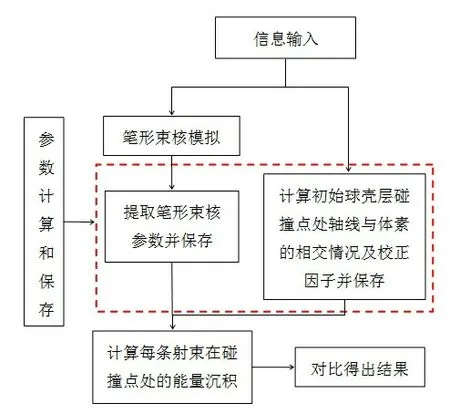
图1 算法流程图Fig.1 Algorithm flowchart

3 实验结果分析与讨论

3.1 实验材料

本文针对不同的射野大小使用的源皮距为100 cm，使用MC 方法的剂量计算是利用开源软件DOSXYZnrc 实现的［16］，传统笔形束核剂量计算是根据文献［7］方法自己编程实现。

实验模体采用Tillikainen 等［7］提出的假设模体：（1）水模体；（2）肺阻块模体，在水模体中距离表层5 cm 的位置放置一个厚10 cm、密度为ρw= 0.3 g/cm3的挡块，该挡块距离射野中心轴2 cm；（3）骨阻块模体，在水模体中距离表层5 cm 的位置放置一个厚5 cm、密度为ρw= 1.85 g/cm3的挡块，该挡块距离射野中心轴2 cm。

3.2 水模体结果

在水模体中，我们使用改进算法、MC 算法和传统算法分别计算不同射野大小下［（3×3）、（5×5）、（10×10）cm2］的深度剂量曲线以及射野大小为（10×10 cm2深度为模体表层下5、10、20 cm 位置处的侧向剂量曲线。

在图2中，FAAA 表示改进算法得到的结果，MC表示MC 方法计算得到的结果，AAA 表示传统算法计算得到的结果，Fs 表示射野大小，D 表示侧向剂量曲线所在深度位置。不同算法得到的深度剂量曲线和侧向剂量曲线分别用不同颜色和不同线型表示。

图2a、图2b 和图2c 表示3 种算法分别在不同射野大小［（3×3）、（5×5）、（10×10）cm2］下的深度剂量曲线，图2d 为两种算法在射野为（10×10）cm2的情况下，模体内不同深度5、10、20 cm 处的侧向剂量分布曲线。两种笔形束核算法与MC 方法的对比结果如表1所示，在不同射野面积大小下两种算法的深度剂量的平均绝对误差相差不大，算法的计算精度基本一致。

表2是传统算法与改进算法分别在水模体中不同射野大小下的剂量计算时间。两种算法均在同一台计算机上进行，系统配置为：64 位，Windows 7，CPU：Intel（R）Core（TM）i5-3450。由表2可知，射野面积越大，计算时间越长。与传统算法相比，改进算法的剂量计算所用时间大大减少。结合表1，两种算法的计算精度基本一致，但改进算法的剂量计算速度提升约2.7倍，大大减少了剂量计算的时间。

3.3 肺阻块模体和骨阻块模体结果

在肺阻块模体中，我们使用传统算法、改进算法和MC方法分别计算射野大小为（10×10）cm2深度为10、16 cm处的侧向剂量分布。在骨阻块模体中，我们使用相同的算法分别计算射野大小为（10×10）cm2、深度为7.5和11.0 cm处的侧向剂量分布。

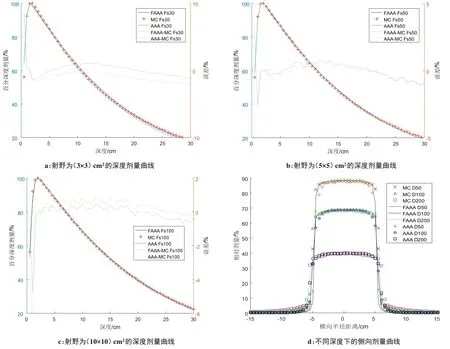
图2 3种算法在水模体中剂量计算结果Fig.2 Results of dose calculation in water phantom using 3 different algorithms

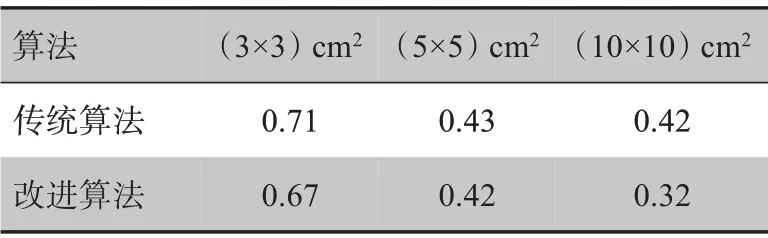
表1 两种算法水在模体中不同射野大小下深度剂量与MC法的对比误差（%）Tab.1 Errors of depth-dose curves of two methods compared with Monte Carlo(MC)algorithm in different field sizes of water phantom(%)

如图3所示，图3a 和图3b 分别为肺阻块模体中距离模体表层10和16 cm位置处的侧向剂量曲线，图3c 和图3d 分别为骨阻块模体中距离模体表层7.5 和11.0 cm位置处的侧向剂量曲线。结合表3，在射野范围内，两种算法在相同模体、相同深度处的侧向剂量分布的误差基本一致，并且都在允许范围内［17］。但是，由于电离不平衡现象，在两种介质的相交界面处和射野边缘均出现了较大的误差。

表4是传统算法与改进算法分别在两种非均匀模体中不同深度处的侧向剂量分布计算时间。两种算法的计算环境与表2相同。与传统算法相比，改进算法大大减少剂量计算时间，同时改进算法在这两种模体中的剂量计算速度提升约2.6倍左右。

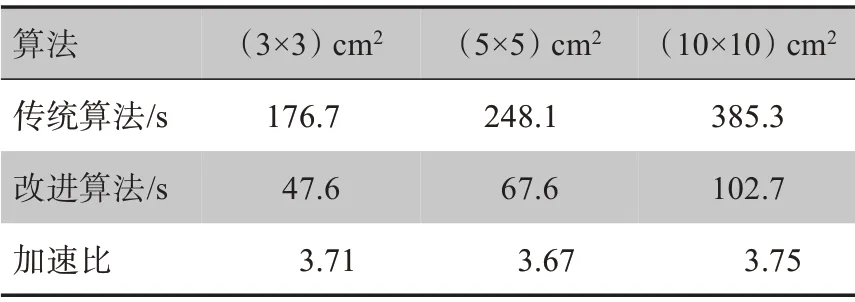
表2 水模体中两种算法在不同射野大小下的剂量计算时间Tab.2 Time for dose calculation of two methods in different field sizes of water phantom

4 结论

图3 3种算法在肺阻块模体和骨阻块模体中射野为（10×10）cm2的不同深度处的侧向剂量分布Fig.3 Lateral dose distribution of 3 algorithms at different depths of field size of(10×10)cm2 of lung block phantom and bone block phantom

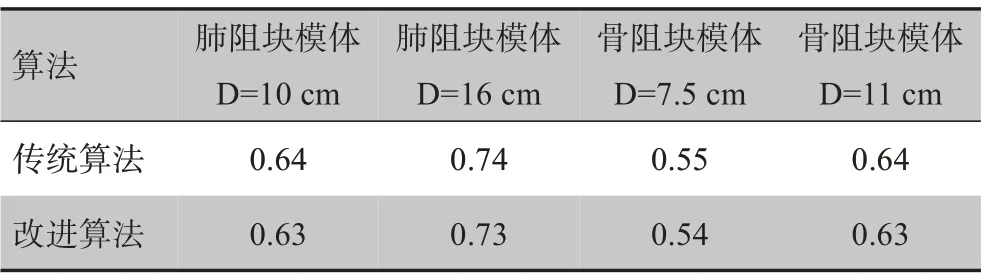
表3 两种算法在不同模体不同深度处侧向剂量分布与MC法对比误差（%）Tab.3 Errors of lateral dose profiles of two algorithms compared with MC algorithm at different depths of different phantoms(%)

在本文中，采用以射束与模体的碰撞点为中心的方法计算剂量分布，在球壳坐标系下利用粒子与模体碰撞后在不同球壳层散射方式的一致性，通过计算射束在初始球壳层碰撞点处轴线与体素的相交情况以及与深度有关的校正因子，得到其它层碰撞点处轴线与体素的相交情况，减少射线追踪法的利用次数，降低剂量计算的复杂度，节省计算时间。

在不同模体内计算剂量分布的实验结果表明，改进算法与传统算法相比，计算精度基本一致，在水模体和非均匀模体中的计算速度提升将近3倍，为剂量计算节省很多时间。同时，在球壳坐标系下以碰撞点为中心计算剂量分布也为后续利用FPGA 和GPU对算法进行加速的研究提供思路。

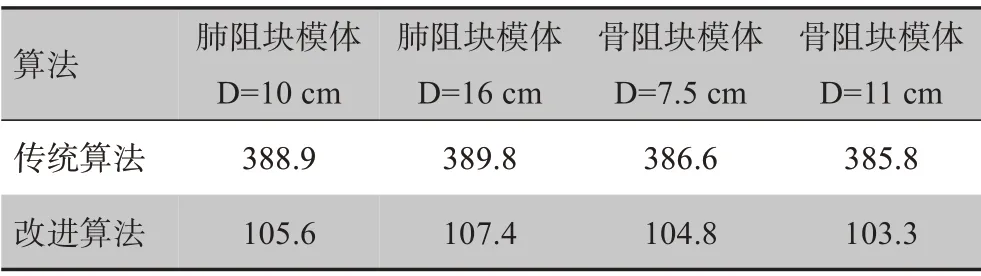
表4 两种算法不同模体不同深度处的侧向剂量曲线计算时间（s）Tab.4 Time for lateral dose calculation of two algorithms compared with MC algorithm at different depths of different phantoms(s)