带参数摄动的时延分段仿射系统事件触发控制
谈超群,刘 飞
江南大学 自动化研究所 轻工过程先进控制教育部重点实验室,江苏 无锡214122
1 引言
分段仿射(PieceWise Affine,PWA)系统因为其概念简单,并且可以有效地对一些实际对象进行分析等优点得到了越来越多的关注。已有研究表明,分段仿射系统可以有效的近似非线性系统,尤其是存在死区、饱和以及滞后等非线性特性的系统[1]。到目前为止,已经有许多关于分段仿射系统的研究成果,比如非线性近似、稳定性分析、控制器设计以及滤波器设计等等[2-5]。
网络控制系统由于其结构简单、易扩展、灵活性好等优点得到了越来越广泛的应用,但其时延、数据丢包、网络带宽受限等问题都会影响系统的控制性能[6]。近年来,许多研究证实,相比于周期采样控制,事件触发控制可以有效地降低网络带宽的占用率,减少通讯资源的浪费[7-8]。事件触发控制的基本思想是“按需传输”,根据提前设定好的事件触发条件来调节控制更新周期。文献[9]第一次提出了周期事件触发控制,在这种控制方法当中,触发条件只需周期性的被检验,并且在每个采样时刻选择是否进行信号传输以及控制率的更新。相比于传统的连续事件触发控制[10],这种触发形式结合了周期采样以及事件触发控制的思想,可以有效地避免Zeno现象的产生并且更加适应实际应用[11]。但是,据作者所知,到目前为止,针对分段仿射系统的周期事件触发控制器设计问题还没有得到充分关注。
另一方面,实际系统的不确定性是不可避免的,且工业过程中的时延也很常见,文献[12-13]研究了网络控制系统存在传输延迟的事件触发控制器设计问题,文献[14]针对含有状态延迟的随机系统,提出了事件触发容错控制器设计方法。本文综合考虑PWA系统存在参数摄动和状态时延,以及网络带宽受限的情况,引入周期事件触发机制减少不必要的信号传输,提出周期事件触发机制与鲁棒控制器的协同设计方法,以保证系统的渐近稳定性。
2 问题描述
网络控制系统结构如图1 所示,其中假设:采样器为时间驱动,控制器、零阶保持器(ZOH)以及执行器为事件驱动。

图1 网络控制系统结构图
考虑如下带有参数摄动的离散时延分段仿射系统:

其中x( k )、u( k )分别表示系统状态及控制器输出,并且x( k )∈X ,X 为Rn的一个子集。bi为仿射常数项,d 为时延系数,、Adi为第i 个子系统的参数矩阵,其中i ∈Ξ ≜{ }1,2,…,N ,这里N >1 是子系统的个数。
假定该系统的参数不确定性为范数有界,即
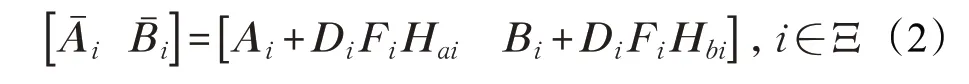
其中Ai、Bi、Di、Hai、Hbi为已知矩阵,Fi为未知时变矩阵,并且满足Fi≤I ,I 是单位矩阵。
注1 事实上Adi也可能出现参数不确定的情况,但因为其处理方法与Ai存在不确定性时的处理方法相同,为简化后续推导过程,本文不再考虑Adi可能存在的参数不确定性。
分段仿射系统中,有界状态空间X 被分割为一组凸多面体形式的作用域,记Xi为第i 个子系统的作用域,也就是X ≜∪i∈ΞXi。当系统状态x( )k ∈Xi时,则第i 个子系统发生作用。并且对于∀i ≠j ∈Ξ ,满足Xi⋂Xj=∅。另Ξ=Ξ0+Ξ1,其中Ξ0为包含原点的作用域的下标集,即bi=0,Ξ1是其余作用域的下标集。记Ω 为所有可能的从一个子系统到其本身或者另一个子系统的切换序列:

假定每一个Xi都可以由一个椭圆集ζi近似,即:
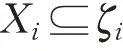
其中:

考虑如下的状态反馈控制器:

其中x̂+(k)定义为:
如图1所示,引入如下的周期事件触发机制来决定是否进行信号的传输:

也就意味着当(6)成立时,系统状态信息被传输并且更新控制率,否则不传输新的系统状态信息以及控制器输出,则(5)可以重新写成:

注2 本文设计的事件触发参数σ 适用于系统的整个动态过程,与系统所处的作用域无关。
本文的主要目标是在选取合适的事件触发参数之后,设计出对应的鲁棒状态反馈控制器,保证系统的渐近稳定性。
3 主要结果
引理1[15]对于任意的矩阵Y 、D 和H ,其中Y 是对称矩阵,Y+DFH+HTFTDT>0 对所有满足FTF ≤I 的矩阵F 成立,当且仅当存在一个常数θ >0,使得Y-θDDT-θ-1HTH >0 成立。
首先,定义误差变量:

根据定义式(7),不等式

始终成立。
因此,控制率(4)可以重新写成:

则闭环系统式(1)可以重新描述为:

定理1 如果存在Pi=PTi>0,Pj=>0,S=ST>0,δij,φij,βij,εij>0,其中i,j ∈Ξ,使得对于分段仿射系统所有可能的切换序列Ω:

均成立,则系统(1)渐近稳定。
证明 针对离散分段仿射系统,在其每个子系统的作用域上分别引入一个Lyapunov函数:

其中Pi∈Rn×n,S ∈Rn×n为对称正定矩阵,且i ∈Ξ。
当x( k )∈Xi,x( k+1) ∈Xj时,其中i,j ∈Ξ ,即分段仿射系统从子系统i 切换到子系统j 时:

根据李雅普诺夫稳定性定理,如果对于系统所有可能的切换序列(包含从一个作用域切换到它本身的情况),ΔV( )k <0 均成立,即不论子系统之间如何切换,分段仿射系统的能量函数始终是衰减的,则系统渐近稳定。
其等价于:
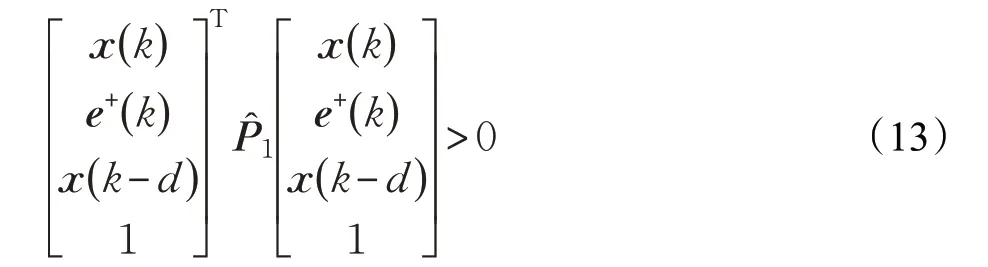
其中:


为进一步处理系统中的仿射项,引入状态椭圆集约束(3),有:
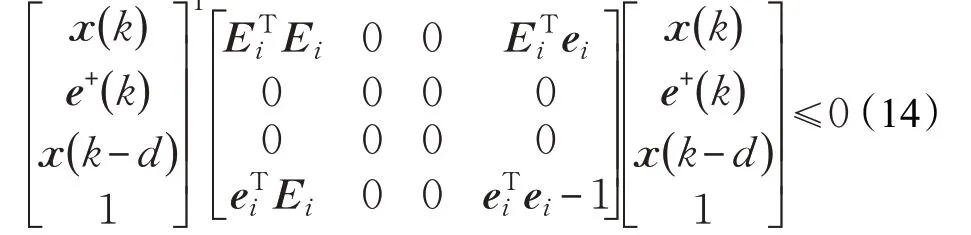
另一方面,不等式(8)可以重新写成:

运用S 过程,将式(13)~(15)进行整合,有:

成立,则式(13)也成立,其中δij>0,φij>0。
则问题转换为求解δij、φij、Pi、Pj、S、Ki使得式(16)成立。
注3 当i ∈Ξ0,此时bi=0,系统(1)相当于一个普通的分段系统,不用对仿射项进行处理,从而不需要再考虑椭圆集信息,显然,由式(11)可以直接推导出式(10)。所以当椭圆集包含原点时,定理1中的式(11)替换成式(10)来求解即可,证毕。
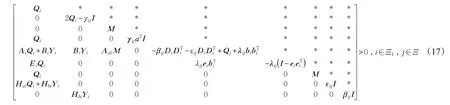

证明 运用Schur补定理及引理1,基于式(11),可得:

必须成立,其中εij>0,βij>0。
通过简单的矩阵变换可得:

其中:


根据矩阵求逆定理:

可以推导出:

运用式(22)及Schur补定理,将式(21)转换为:

另因为

可得:

注4 对于i ∈Ξ0,此时bi=0,不用对仿射项进行处理,从而不需要再考虑椭圆集信息,由式(17)可以直接推导出式(18),此处证明过程省略。
4 仿真结果
考虑如下的PWA系统[16]:



五个子系统被分割为:

将式(22)离散化,T=0.1 s,控制目标是将系统稳定到原点位置。
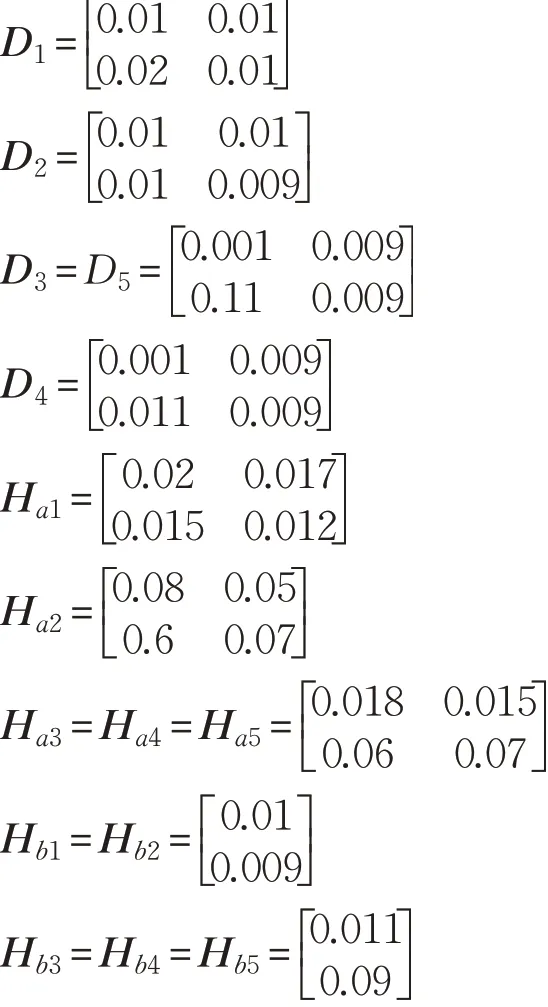
在下面的仿真过程中,用

来衡量信号传输减少的情况。


由图2~4可以看出,在周期事件触发机制减少了信号传输次数之后,基于定理2设计的周期事件触发控制器仍然可以保证分段仿射系统渐近稳定性。另外,图4中0.8代表触发条件成立,0.2表示不成立。由表1可以看出,通过增大σ 可以进一步减少信号的传输次数及控制率的更新,当然此时系统的动态性能也会相应变差,这在以往的研究中已有证实[11],此处不多加赘述。此外,由图5可以看出,当时延进一步增大到d=9 时,系统仍然稳定,证明了本文方法的有效性。
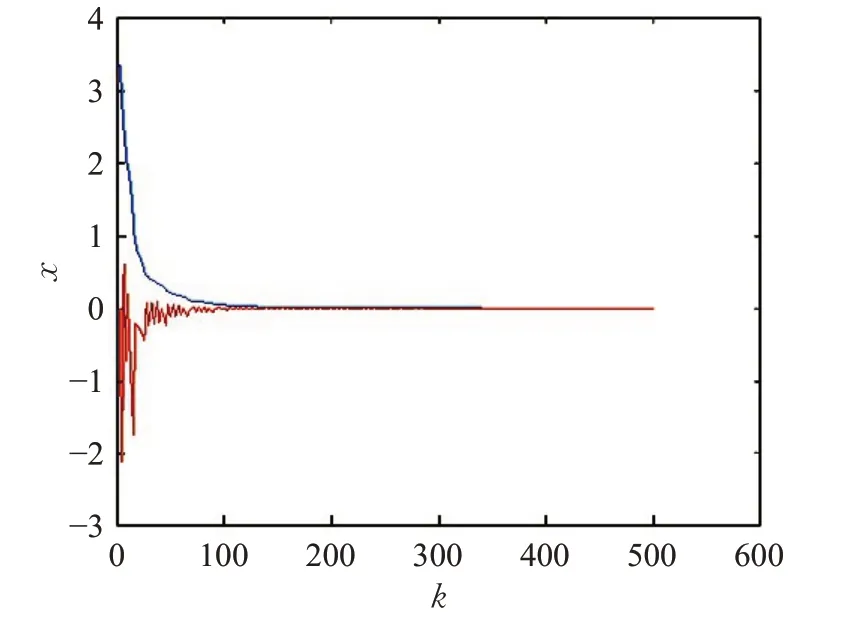
图2 系统状态轨迹(d=2,σ=0.6)
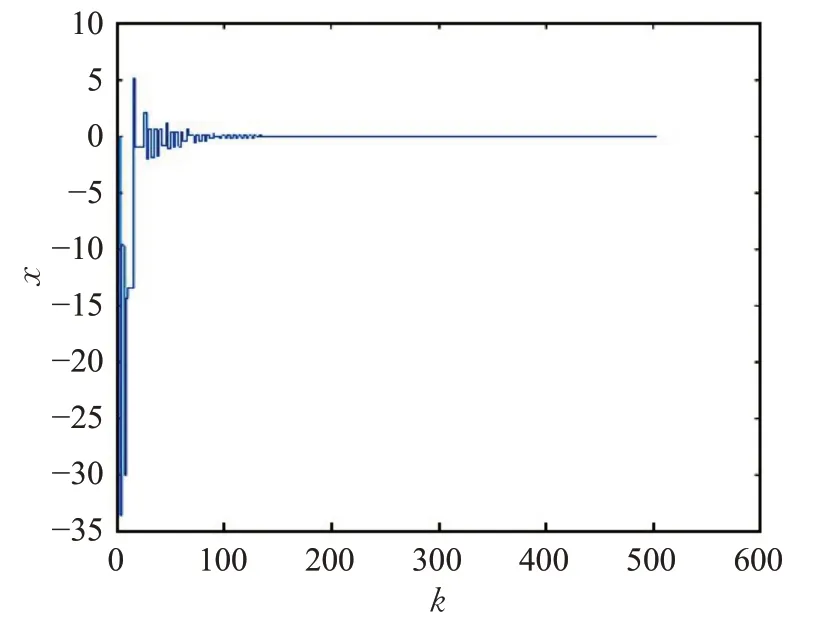
图3 控制器输出

图4 事件触发时刻
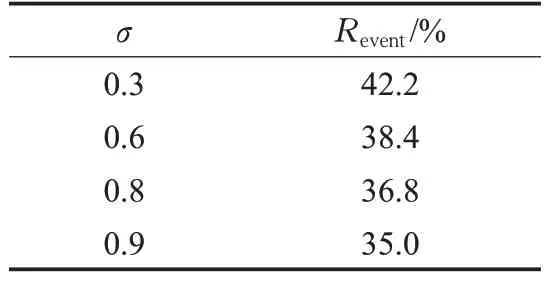
表1 不同σ 对应的信号传输率
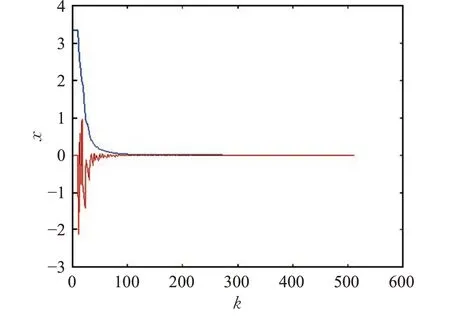
图5 系统状态轨迹(d=9,σ=0.6)
5 结束语
本文针对同时含范数有界参数不确定性以及状态时延的网络化分段仿射系统,提出了周期事件触发机制及鲁棒控制器的协同设计方法。实验结果证明,相比于周期采样控制,本文设计的方法可以在保证系统渐近稳定的同时,减少信号的传输从而减少网络带宽占用。当然本文还存在保守性较大的问题,后续工作将对此加以改进,另外也可以对含有时变传输时延或者随机分布式时延的分段仿射系统做进一步研究。

