二维逐步正交匹配追踪算法
邵 然,沈 军
1.哈尔滨工程大学 信息与通信工程学院,哈尔滨150001
2.上海无线电设备研究所,上海200090
1 引言
2006年,Donoho、Candes等人[1-2]提出的压缩感知理论,将信息的压缩和采样过程合为一体一并进行,开辟了计算成像新领域。作为最早也是最有名的应用之一,莱斯大学的单像素相机[3]为压缩感知成像指明了研究方向。但无论是何种系统,都会面临图像作为二维信号这一难关。直接的方法,比如在单像素相机中应用DMD模块,或者将输入二维信号直接降维一行行扫描重构成像,都面临计算效率低、块相应明显或者重构图像视觉效果差的问题[4]。而将采样矩阵和稀疏表示对场景进行适配,比如Jiang等人[5]提出的基于玫瑰花瓣扫描的红外成像系统,虽有较好的重构效果,采样矩阵却受限于场景难以得到推广。
在此基础上,针对二维信号的采样问题,Ghaffari等人[6]提出了二维观测模型(2D Measurement Model,2DMM)。通过两次采样过程,使得任意类型的二维矩阵都可以变为行列稀疏的方形矩阵,进而便利的压缩感知处理。这种框架突破了原有一维信号压缩感知的限制,在不进行各种变换的情况下保留了行间相关性信息,并进一步降低了采样后数据量。在同一篇文章中,还提出了基于此框架的2D-SL0 重构算法,该算法是基于一维信号的l0算法思想改进得到的。该文指出,根据传统重构算法设计思路得到二位重构算法是可行的。随即,Fang等人[7-8]提出了基于2DMM的OMP算法和2D-OMP算法,实现了较快速度下的高质量重构。在此基础上,田文飚等提出了2DMM-SP 算法[9],也就是二维观测模型下的SP算法(为了对应,下文称其为2D-SP算法)。
本文将借鉴该设计思路,对现有算法进行分析与改进,提出二维逐步正交匹配追踪重构算法(2D Stagewise Orthogonal Matching Pursuit,2D-StOMP)。提出的算法能够对图像二维观测得到的信号精准恢复,运算时长得以控制,信噪比和恢复效果则得到很大的提升。
2 二维图像压缩感知模型
2.1 压缩感知理论与二维图像应用难题
经典压缩感知框架中,自然信号f 利用某种逆变换Ψ 来得到稀疏表示x,之后经过测量矩阵Φ 采样得到测量值y,即:

其中,感知矩阵A=ΦΨ 。若其满足约束等距特性(Restricted Isometry Property,RIP 准则)[2,10-11],则通过求解一个l1优化问题便可以还原出原信号的稀疏表示,即稀疏表示的重构信号:

通过巧妙的设计测量矩阵和变换矩阵,使应用场景中信号的采样率突破奈奎斯特定理的限制,是压缩感知突出之处。但对于上述模型,若按照相关模型一贯的假设x ∈ℝN,y ∈ℝN,原二维信号为f ∈ℝM×N,即原信号为图像这种二维信号,则Φ 与Ψ 则难以设计。
为了能够将压缩感知应用到图像处理中,一般将图像进行变换后,按行或者列进行采样,转换为ℝMN大小的一维信号进行分步处理。该方法存在很多问题:若有一行或者一列重构失败会导致黑色或白色条状或块状纹路,影响图像可读性和视觉效果;图像行间信息遭到破坏;由于一维信号进行小波变换等处理的要求,使得图像行或列必须是2 的整数次幂,应用前景被限制;且图像行列间稀疏度往往有大幅度变化,简单的循环无法妥善处理。虽然改进重构算法,进行分块处理,可以在一定程度上改善这种状况,但在信息量被压缩的情况下,行间信息仍很难得到保留,直到2DMM被提出。
2.2 2DMM
二维观测模型(2DMM),由Ghaffari 等人[6]于2009年提出,不过类似的设计思想在关联领域文献里也早有论述[12],比如,在雷达成像领域它有一个名字叫二维稀疏信号模型(2D Sparse Signal Model)[13],其核心思想便是,经过两次变换和采样来得到规整的采样值,同时保留行间信息。本文将采用其中一例模型[8]。
首先,假设输入二维信号f 在Ψ 变换域上是k 稀疏的(k ≪N2),其本身是一个N×N 大小的矩阵,稀疏表示出的矩阵大小不变的信号为x,即:

而对于相应的测量值,则也需要经过两次测量:

感知矩阵A=ΦΨ 。进一步的,根据2DMM中的证明可以得到:

其中,字典(dictionary)矩阵D=A ⊗A,⊗表示两个矩阵的克罗内克积。此时各个矩阵大小如表1所示。

表1 矩阵大小
因此,该模型下的优化问题则近似表示为求下式的l2范数最小值[7]:

下文中,通过分析现有重构算法和改进型,可以得到上式的求解方法。
在2DMM下,对图像的长宽等不再有限制,且采样得到的数据量大幅度降低。但传统的压缩感知重构算法不再适用于这一观测模型,因此设计新的二维重构算法便势在必行。
3 改进的二维重构算法
压缩感知重构算法始于凸优化问题,而应用最广泛的便是以正交匹配追踪算法(OMP)为代表的贪婪算法。在此基础上,其每次选择的原子(atoms)增加数量并进行正则化处理,便得到正则化正交匹配追踪算法(ROMP);而对每次选择的原子的数量进行选取条件和复杂度计算后的调整,便可以得到相应的子空间追踪算法(SP)等;进一步的,将每一次循环得到的原子数量不规定为固定数,而是符合迭代阈值的若干数,为逐步正交匹配追踪算法(StOMP);最终,如果连稀疏度与每次原子数也不予规定,能够直接应用于各场景的,为稀疏度自适应匹配追踪(SAMP)。由此可见,每次迭代时的原子数量同阈值、算法效率都有密切关系[14-15]。因为每次迭代都应该选择与残差相关性最佳的原子,单纯的增加每次的原子数并不一定能够增加效率,这种情况下残差增加,既导致迭代次数增加,又会影响最终重构精度。因此应该选择恰当阈值,使得每次迭代原子数量大致在稀疏度K 左右,此时其处于一个平衡点,使算法整体效率得到很大提升。
在二维压缩感知重构算法的设计上,同样可以借鉴这种思路,增加2D-OMP 算法中每次循环的原子数量,在每次循环迭代求式(6)最小值的过程中,从构造的字典每次选取符合阈值的、与残差最相关的几列原子,得到子集后一同进行处理,这便是2D-StOMP算法。该算法控制了复杂度,并提高了运算效率,其中,最关键的便是每次循环选取原子的阈值[15]。由文献[16]可知,提出的StOMP 算法,其原子选取的阈值依据内部噪声指定。在一维信号处理过程中,经分析其噪声为。其中rs为重构算法残差,n 为重构序列长度。在此之上再乘以2 到3 的增幅ts,便得出阈值。在二维重构算法中,因为系统设计和观测矩阵上高度相似性,每次循环重构序列长度为M ,而增幅ts由经验[16]取值为2,因此新设计算法的阈值为。下面将仿照文献[16]对此进行证明。

又因为:

故:
综上:

其后,第S 次迭代按照公式(11)替代公式(7)中z,同理可证:
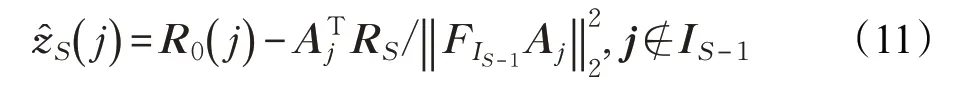
算法步骤如下。
(1)输入:测量值y ∈ℝM×M;感知矩阵A ∈ℝM×N;稀疏度k ∈ℤ+。
(2)初始化:输入输入量;残差R=y;字典矩阵D=A ⊗A:
阈值增幅ts=2;原子计数δ=0。
主循环 循环数t 从1到k:
2.更新D=D∗F;
4.选取C 中比Th 大的δ'个元素,δ'=δ+δ';
5.更新( Iδ-δ'+1,Jδ-δ'+1)到( Iδ,Jδ)分别为上述元素的坐标;
6.更新标记矩阵F,上述( )
I,J 位置置零;
8.更新
4 理论分析与仿真
4.1 理论分析
2D-StOMP 算法的求解过程必定符合贪婪算法的内在逻辑,对其算法进行的详细分析既要包含有效性分析也要包含复杂度分析。在某种程度上,有效性影响算法重构精度,复杂度影响算法运算时长。
4.1.1 有效性分析
当且仅当一个压缩感知研究模型符合衡量其的三个定量指标,才可以说这个模型是严格压缩感知意义上的完全可重构模型。而这三个指标,即RIP准则[2,10](RIC常数)、Spark 判别理论(Spark 常数)[17]和相关性判别理论(互相关系数)[18],是有内在联系的。一般来讲,一个模型中设计的观测矩阵,只要符合其中一个指标的判定,就可以说这个观测模型的设计是有效的,也可以直接调用相关的重构算法进行信号恢复。本文将使用RIP准则来进行判定,将其作为引理1引入。
引理1(2k 阶约束等距性)

当且仅当式(12)成立时,式(13)有解。其中,x ∈ℝN,为k 阶稀疏信号;常数δ2k∈(0,1)。该公式证明参考文献[2,10]。
引理2 如果A ∈ℝp×q,B ∈ℝr×s,则下式成立。

该公式证明参考文献[19]定理3.7。引理2 提供了判定矩阵克罗内克积的RIP参数计算方法。由引理1和引理2 可证明本文涉及到的2DMM 是有效的压缩感知模型,如定理1所述。
定理1 对于二维矩阵信号x ∈ℝN×N,若其每行每列皆为k 稀疏,且感知矩阵A=ΦΨ 符合RIP 准则,则min‖ ‖̂2有解。其中,字典矩阵D=A ⊗A。

4.1.2 复杂度分析
2D-StOMP 算法复杂度为每次循环运算量与循环次数的乘积,详细分析如下。
(1)初始化:计算字典矩阵复杂度为M×N 矩阵的克罗内克积运算的复杂度,即
(2)主循环:映射部分,由表1 中所列和文献[8]中3.4.1 小节计算得,更新C 时运算量最大,为其余更新R 等运算量逐次增加,最大为
综上所述,由于kδ <M2N2,所以主循环算法复杂度为。而采样率不同,则δ 与M 的大小难以判断,可将复杂度定为O(M2N2+kMN2) 。相比较而言,虽然2D-OMP文献中复杂度为O(kMN2) ,但其未将初始化中克罗内克积运算统计在内。如果统一标准,两种算法都移除克罗内克积的运算过程,那么两者复杂度相同,这也意味着,理论上两种重构算法的运行时长应该相差无几。另一方面,如果按照文献[9]的标准,计算极限条件下(每次只选入一个原子)的算法复杂度,也不考虑克罗内克积,则该算法复杂度比2D-SP 算法的要大。但极限条件下两者实质退化为类似于2D-OMP 的算法,并没有实际意义;在非极限条件下两者复杂度相近。
除此之外,新算法若与二维信号一维化后再进行OMP 重构的传统方法相比更大幅度地降低了复杂度。
4.2 仿真实验
为了验证新设计算法的优越性,本文设计了仿真实验。实验采用二维随机高斯矩阵为测量矩阵,二维DCT 变换矩阵为变换矩阵;重构算法包括2D-StOMP、2D-SP、2D-OMP、2D-SL0 和1D-OMP;平台电脑操作系统为64位Windows7,双核2.10 GHz CPU,内存6 GB。
重构算法恢复质量的评价标准有人眼视觉效果评估、峰值信噪比PSNR、运行时长等。实验结果和分析如下。
4.2.1 视觉效果分析
实验输入图像有四例:战斗机的红外图像;图像处理常用例子Lena 的灰度图像;高光谱图像测试集Pavia University Scene 的一帧部分高光谱图像;实验室自行采集的远处客机的红外图像。图片大小:前三者为256×256 像素,最后一张为128×128 像素。采用此四例能够充分展示在不同图像类型、背景、内容下不同重构算法恢复效果的细节。
视觉效果实验采样率为M/N=ε=0.55 。由于2DMM下实际上进行了横纵两次采样,因而严格意义上的采样率,即采样信息量与输入信息量的比值为ε2,即0.3。实验添加了采样率ε 为0.3情况下一维压缩感知重构算法作为对照组。实际上,由于压缩感知理论限制,一维压缩感知框架在采样率0.3 以下就无法恢复出图像,因此在0.3以下2DMM框架具有独特的优势。
在采样率相同,稀疏度同取64的情况下,各重构算法恢复效果如图1 所示。如图所示,可见在低采样率同等条件下,2D-StOMP的恢复效果和PSNR 优于其他重构算法:既没有明显的块效应,也没有重构失败导致的黑色条纹,很大程度上保留了行间信息,降低了重构中由于收敛不当引入的噪声。特别的,与2D-SP 相比,虽然PSNR 大致接近,但在一些细节部分,诸如Lena 图像中的帽子和脸部部分,前者视觉效果上要更加细腻(下文数据将会证明,随着采样率增加,两者差距将进一步拉大)。
4.2.2 峰值信噪比与运行时长
仿真算法对同一图像进行重构,计算输出图像同输入图像的峰值信噪比(PSNR)和运行时长,对不同采样率条件下,100次运算取得平均值。

MSE是指图像均方根误差。
由于采样率在0.55(即一维压缩感知采样率为0.3)以下时,一维重构算法很难恢复图像,因此对比中未列入1D-OMP算法。运行结果如图2所示。
由图2 及表2 可知,2D-StOMP 算法在采样率为0.3及以上时,PSNR要优于其他算法。

图1 视觉对比图

图2 重构算法PSNR对比图

图3 重构算法运行时长对比图

表2 不同算法在稀疏度变化时恢复图像所用时间和PSNR
由图3 及表2 可知,2D-StOMP 算法运行时长要高于其他算法一到两个数量级,但并未超过秒级。除非是某些对时间极其敏感的应用场景,比如红外制导、自动驾驶、武器控制等等,在其余场景(比如高光谱成像等),考虑到其相较其余二维重构算法更为优秀的恢复效果、相较一维重构算法更加优越的压缩比,一定时间上的牺牲可以接受。并且,随着电子元器件的进步和计算能力的不断提高,上述算法运行时长间的差距会越发不明显。
综上所述,这里所设计的仿真实验,有效地证明了2D-StOMP 算法相比较于其他算法的优越性。这种优势体现在,同等采样率下,该算法对同一图像的重构效果更佳,且重构时长没有过度增长;且经过编程语言的更替与改进,重构时长也不会有数量级上的差距。
归结起来,这是二维观测模型和灵活选取迭代原子数量叠加的双重效果。前者保证其相对于一维压缩感知的优势:即使经过改进的稀疏矩阵,在压缩感知步骤中的稀疏变换后对信号的采样,亦会导致其丢失行间信息;相对应的,由于二维观测模型是针对二维矩阵信号,尤其是图像而设计的,因而其更能适应图像行与行间、或者列与列间稀疏度大幅度变化的特殊情况,也能更好地适应图像压缩感知应用场景,与此同时,由于二维观测模型中两次变换的存在,观测所需的信息量也被再次压缩,促成更高效率的压缩感知算法。后者则保证了其相对于现有二维重构算法的优势:固然,对于2D-OMP等算法而言,单纯的增加迭代次数及稀疏度能在一定程度上改善恢复效果;但迭代后的残差却没有任何控制手段,由于残差变化幅度大,选取原子整体上便容易“背离”原始数值,同时,由于同样的原因,变化幅度大导致不易收敛到某一节点,平均计算单次迭代中计算量反而增加,直接导致算法运行时长大幅度增加(达到同等效果往往需要运算时长增加两个数量级以上),这限制了通过增加迭代层次来改进算法的途径,诸如2DSP 等固定单次迭代原子数量的算法也存在类似问题;而通过选取阈值灵活选择原子,本文算法能够控制每次迭代后残差都保持在一个范围内,更为下一层迭代提供了更佳的阈值选取标准,因而理论上其在同等时长下理应得到更高的恢复精度,且图像行列间关联性越高,稀疏度越大越有利于该算法,这在视觉仿真实验中亦有所体现,人体面部细节上该算法明显优于其他算法。
结合前文分析,考虑到2D-StOMP 算法与2D-OMP等传统算法在复杂度这一因素上相差不大,这意味着,若采用更加契合循环的程序语言对本文算法进行实现,其运算时长不会同其他算法产生数量级上的差距:众所周知,Matlab 语言不善于处理多次循环,以及大小不确定数组的内存空间分配。因此,相信经过进一步的优化和改进,届时2D-StOMP算法的运行时长将会得到有效降低,算法的性能也能有所提高。
5 结束语
针对二维信号压缩感知重构算法存在的相关问题,本文结合一维重构算法的设计思路,提出了2D-StOMP算法。提出的算法通过每次循环迭代时选择契合阈值条件的原子来提高重构准确性。理论分析和仿真实验表明,本文算法解决了现有的块效应和部分行列重构失败问题,重构效率得到很大提升,示例图像的重构质量得到了明显改善。

