前向安全的椭圆曲线数字签名方案

张 平，栗亚敏

河南科技大学 数学与统计学院，河南 洛阳471000

1 引言

在互联网高速发展的今天，越来越多的密码系统被应用于安全性较差的场合，密钥保护势在必行。在公钥密码体制中，密钥泄露会给用户带来极大的损失。为了减小密钥泄露的可能，早期的办法包括：秘密分享系统、门限密码系统和前摄密码系统。但是这些系统的开销很大，因此有很大的局限性。密钥泄露是无法避免的，但是前向安全技术可以减少密钥泄露带来的损失。这个技术的核心就是系统时间划分方法，它的具体思想是将签名系统的有效期划分为若干个时间段，私钥随着时间段的变化而变化，公钥保持不变，即使某一时间段的私钥泄露，也不会影响到以前各时间段签名方案的安全性。

椭圆曲线密码体制是基于椭圆曲线的一种公钥体制，椭圆曲线理论是包含代数几何、代数数论和解析数论这三门学科的综合性学科。由于早期的基于有限乘法群的密码体系不安全，研究人员提出了能否用其他有限群来代替有限乘法群的问题。鉴于此，Koblitz[1]和Miller[2]提出了椭圆曲线密码体制（ECC），该体制是目前安全性最高的公钥加密算法。1997 年，Anderson[3]在CCCS’97 上首次提出了前向安全的思想，但是只给出了简单的概念性描述，并没有给出具体的使用方案。随后，Bellare 和Miner[4]在Crypto’99 上给出了前向安全的详细定义，并且构造出首个有效的具有前向安全的签名体制。2003年，Hu[5]等人提出了第一个基于双线性配对的前向安全签名方案。2004年，徐丹等人[6]提出了一种基于离散对数问题的强健的密钥演化签名体制。2006 年，符茂胜等人[7]利用关联因子构造了一种基于ECC的前向安全数字签名方案。2013年，徐光宝等人[8]在Guillou-Quisquater 签名体制和Rabin 密码体制的基础上提出了一个强前向安全的数字签名方案。2015年，陈辉焱等人[9]提出了一种基于椭圆曲线的前向安全签名；同年，甄平等人[10]利用Chebyshev 公钥算法，提出一种基于身份的前向安全数字签名算法。2016 年，周克元[11]设计了一种具有消息恢复功能的椭圆曲线数字签名方案，该方案不仅能抗伪造签名攻击，还具有前向安全性；同年，李亚荣等人[12]提出一个前向安全代理签名方案，该方案满足前向安全代理签名的所有安全性要求；李顺波等人[13]借助单向散列链技术构造了一种基于ElGamal 体制的数字签名方案。2017 年，李靳元等人[14]针对基于椭圆曲线的前向安全数字签名方案所存在的安全性漏洞问题，给出伪造签名的方法，并对方案进行了改进。随后，一些前向安全的特殊数字签名方案[15-19]被相继提出。

现有的前向安全的签名方案大多数都是建立在大素数因子分解和有限域离散对数问题上的。目前安全性，最高的公钥加密算法是椭圆曲线密码体制（ECC）。相对于RSA 密码体制和DSA 密码体制来说，椭圆曲线具有以下优势：（1）有限域上的椭圆曲线资源丰富；（2）求解椭圆曲线上离散对数问题（ECDLP）比有限域上离散对数问题更加困难；（3）在相同的安全强度下，椭圆曲线密钥长度更小，更加节省计算资源和存储空间。但是已有的椭圆曲线签名方案大部分没有前向安全性。本文将椭圆曲线密码体制的优势与前向安全的概念相结合，在ECDSA方案的基础上，引入系统时间划分方法来减少密钥泄露带来的损失，从而构造出一种基于椭圆曲线的前向安全的签名方案，然后在随机预言模型基于ECDLP 问题的困难性证明该方案的前向安全性，并将该方案与同样具有前向安全性的周克元方案进行效率比较。

2 预备知识

2.1 椭圆曲线离散对数问题

椭圆曲线离散对数问题是椭圆曲线密码体制的核心。椭圆曲线离散对数问题就是对于椭圆曲线E(GF(q))上任意两点G 和Q，有Q=dG，在已知G 和Q 的前提下求出小于q 的正整数d。己知d 和G 计算Q 比较容易，但是己知Q 和G 计算d 则很困难，这便是椭圆曲线加密体制的核心。

椭圆曲线密码体制的安全性基于椭圆曲线离散对数问题，也就是求解ECDLP 算法的时间复杂度。和一般的有限乘法群上的离散对数问题所不同的是，有限域上的椭圆曲线离散对数问题的求解难度更大，求解过程更复杂，在多项式时间内无法被所有的已知算法求解。在一般的离散对数问题中，有限域上的代数运算包括域加法和域乘法两种运算，这使得一般的离散对数问题可以在亚指数时间内被求解。然而，在椭圆曲线离散对数中的代数运算只包含椭圆曲线上的点加这一种基本运算。这导致的结果是除了一些非常特殊的椭圆曲线外，在亚指数时间内所有的离散对数求解算法都无法求解椭圆曲线离散对数问题。

2.2 前向安全体制

前向安全体制中的密钥更新过程如图1所示，在前向安全的密码系统中，假设密钥演化体制中存在一个可信的第三方TD（Trusted Dealer），它拥有一些特殊的密钥，这些特殊的密钥用来更新签名体制中的密钥。这里假设整个体制的时间被划分为N 个时间段。用户的公钥自始至终都保持不变，但是用户的私钥要在每个时间段的开始进行一次更新。在整个密钥更新过程中，F表示单向的密钥更新函数，第j-1 个时间段的私钥SKj-1通过计算函数F 可以得到第j 个阶段的私钥SKj，要保证由SKj计算SKj-1是困难的。由于在某个特定的时间段j 内，用户在进行签名时用到的只是该时间段的私钥SKj，所以该时间段的密钥泄漏，只会损失系统当前的安全性和以后的安全性，却不会危害到系统之前的安全性。

图1 前向安全的密钥更新过程

密钥演化体制KE=(Gen,Upd,Sign,Vrfy) 由以下四部分组成[20]。

Gen（密钥生成算法）：(PK,SK0,S)←Gen(1λ,…)该算法是概率多项式时间的算法。输入的是安全参数λ和其他系统参数，输出为公钥PK 、初始私钥SK0。其中S 代表陷门，当系统中存在可信的第三方TD时，将陷门S 给TD，如果系统中不存在可信的第三方TD，则丢弃陷门S。

Upd（私钥更新算法）：SKj←Upd(j,SKj-1)该算法是确定多项式时间的算法。输入的是前一时间段的私钥SKj-1，输出为该时间段的私钥SKj。当系统中存在可信的第三方TD时，则该过程与第三方TD共同完成。

Sign（签名生成算法）：(j,s)←Sign(j,SKj,m)该算法是概率多项式时间的算法。输入的是该时间段的私钥SKj和消息m，输出为该时间段消息m 的签名(j,s)。

Vrfy（签名验证算法）：{ }0,1 ←Vrfy(PK,M,(j,s))该算法是确定多项式时间的算法。输入的是公钥PK 、消息m 和消息m 所对应的签名(j,s)，输出为0 或1，其中0 表示拒绝接受签名，1 表示同意接受签名。当Vrfy(PK,M,(j,s))=1 时，签名(j,s)是消息m 在j 时间段的有效签名。

3 ECDSA签名方案

3.1 参数选择

GF(q)是有限域，E:y2=x3+ax+b(mod q)（a,b ∈GF(q)，且4a3+27b2≠0）是该有限域上的椭圆曲线，G是椭圆曲线上的一个基点，ord(G)=n，n 是一个大素数，是余因子，d 是签名私钥，Q=dG 是签名公钥，是美国NIST和NSA 设计的一种安全Hash 算法，输入信息长度一般小于264bit。D={ }q,a,b,G,n,h ，Q、H 公开，d 保密。

3.2 签名生成

签名者A利用公私钥对消息m 签名：

（2）计算kG=(x1,y1) ，r=x1mod n ；若r=0 ，跳至步骤（1）。

（3）计算e=H(m)。

（4）计算s= k-1(e+dr)mod n ；若s= 0 ，则跳至步骤（1）。

（5）签名结果为(r,s)。

3.3 签名验证

（2）计算e=H(m)。

（3）计算w=s-1mod n。

（4）计算u1=ew mod n 和u2=rw mod n。

（5）计算X=u1G+u2Q=( x2,y2)。

（6）若X=0，拒绝该签名。

（7）计算v=x2mod n，若v=r ，则接受该签名，否则拒绝该签名。

3.4 安全性分析

该方案不具有前向安全性，即一旦私钥d 泄露，之前所有的签名都会被破坏，从而导致整个密码体制崩溃。为减少密钥泄露带来的损失，需要设计出一个新的密码体制，使得某一时间段私钥的泄露不影响以前各时间段签名体制所提供的安全保障。

4 改进的椭圆曲线签名方案

针对原签名方案存在的安全问题，进行改进，引用徐丹等人[6]密钥更新方法，将系统的有效时间分为若干个时间段，在每个时间内进行密钥演化，提出了一个新的椭圆曲线签名方案。假设在系统中存在可信第三方TD，其持有一些用来更新密钥的秘密。

4.1 参数选择

GF(q)是有限域，E:y2=x3+ax+b(mod q)（a,b ∈GF(q)，且4a3+27b2≠0）是该有限域上的椭圆曲线，G是椭圆曲线上的一个基点，ord(G)=n，n 是一个大素数，是余因子，是美国NIST和NSA设计的一种安全Hash算法，输入信息长度一般小于264bit。假设在系统中存在可信第三方TD，其持有一些用来更新密钥的秘密。假设系统的有效时间被分为N 段。

4.2 密钥生成

（1）随机选择z 次多项式f(x)=a0+a1x+a2x2+…+azxzmod n。

（2）初始私钥SK0=f(0)=a0，公钥为PK=(a0G,a1G,…,azG)。

（3）随机选择xi∈[1,n-1]，1 ≤i ≤z，将f(xi)分配给TD。

4.3 密钥演化

该部分引用徐丹等人[6]密钥更新方法。签名者和TD 用分布式的方法共同计算SKj=f(j)(j ≥0) 。在密钥更新过程中需要TD 的参与，假设有z 个TD，每个TDi有一个共享份额f(xi)(1 ≤i ≤z)，xi互不相同，且远大于时间段数N ，签名者拥有时间段j-1 的私钥f(j-1)。假设签名者和TD 之间有保密信道。不妨假设签名者是TD0，则由Langrange 插值公式可知：

（1）每个TDl(1 ≤l ≤z)，随机选z 元变量(al,z,…,al,1)，构建一个z 次多项式，通过保 密 信 道 将hl(xi) 发 送 给TDi(1 ≤i ≤z) ，设F(x)=

（2）每个TDl(1 ≤l ≤z)，计算自己的共享份额F(xl)=

（3）每个TDl(1 ≤l ≤z)，通过保密信道发送F(xl)给签名者TD0。

（4）签名者TD0根据F(x0),F(x1),…, F(xz) 通过Langrange插值公式计算F(x)的常数项系数，则计算出其在第j 时间段的私钥

4.4 签名生成

4.4.1 第一种签名生成方案

签名者A利用公私钥对消息m 签名：

（2）计算kG=(x1,y1)，r=x1mod n ；若r=0，跳至步骤（1）。

（3）计算e=H(m,r)。

（4）计算sj=k-1(e+SKj⋅r) mod n；若sj=0，则跳至步骤（1）。

（5）签名结果为(j,(e,sj) )。

4.4.2 第二种签名生成方案

由于第一种签名生成方案中存在模逆运算，效率势必会很低，对此作出改进。

签名者A利用公私钥对消息m 签名：

（2）计算kG=( x1,y1)，r=x1mod n ；若r=0，跳至步骤（1）。

（3）计算e=H(m,r)。

（4）计算sj=k+e ⋅SKjmod n ；若sj=0 ，则跳至步骤（1）。

（5）签名结果为(j,(e,sj) )。

4.5 签名验证

验证者B 验证(j,(e,sj) )是否是A 对消息m 的签名（仅对第二种签名生成方案进行签名验证）：

（1）检验e,sj∈[1,n-1] 是否成立，若不成立，返回拒绝签名。

（3）计算r'=x2mod n。

（4）验证e=H(m,r')是否成立，若成立，则接受该签名，否则拒绝该签名。

4.6 正确性分析

5 安全性分析

（1）与ECDSA方案相比，改进方案可以抵抗随机数攻击。很多人都提到不同消息使用同一签名方案进行签名时，使用相同的随机数（这种概率非常小）是不行的[21]，原因是：如果使用ECDSA方案对不同消息进行签名时使用了相同的随机数，就可以用一个二阶的线性方程组解k=(s'-s)-1(e'-e)mod n ，进而解出私钥d=r-1(sk-e)mod n。

如果运用改进方案分别在不同的时间段i、j，对两个不同消息使用相同的随机数进行签名，就会得到方程组，由于不同时间段的私钥是不同的，因此无法通过方程组求得两个私钥f(i)和f(j)。所以，改进方案可以抵抗随机数攻击。

（2）密钥演化算法具有前向安全性。根据徐丹等人[6]密钥更新方法可知，该方法即使是在z 个私钥泄露的情况下，依然是选择消息攻击下存在性不可伪造的。敌手无法通过第j 时段的私钥SKj求得第j-1 时段的私钥SKj-1。

（3）签名算法具有前向安全性。当敌手获得第j 时段的私钥时，他无法通过第j 时段的私钥去伪造第j-1时段的签名。由sj-1=k+e ⋅SKj-1mod n 可知，如果敌手要伪造第j-1 时段的签名(j-1,(e,sj-1))，需要知道SKj-1。而由密钥演化算法的前向安全性可知，敌手无法通过第j 时段的私钥SKj求得第j-1 时段的私钥SKj-1，从而保证了签名算法的前向安全性。

通过以上分析可知，本文解决了敌手在得到某时间段的签名私钥后，在不知道之前时间段私钥的情况下能够伪造任意时间段签名的问题。

（4）在随机预言模型下，若存在敌手A 以不可忽略的优势ε 攻破改进方案，那么存在算法B 至少以优势ε'=ε/N-negl(n)的优势解决ECDLP 问题，这里N 是时间段总数。

证明 假设攻击者A以优势ε 攻破改进方案。算法B的输入为G，G ∈E。B模拟A的挑战者如下。

准备阶段：B 设定时间段总数为N ，并猜测A 伪造时间段J(0 ≤J ≤N)的签名。B 在有限域GF(q)上选择椭圆曲线E ，并在E 上选择一基点G ，ord(G)=n。B选择哈希函数H ，z 次多项式。B 将公钥PK=(a0G,a1G,…,azG)发送给A。

查询阶段：哈希查询：模拟哈希查询，B包含哈希查询列表LH和签名列表LS。所有列表初始为空。当A对m 进行哈希查询时，B 首先检查m 是否已出现在列表LS中，若没有，B进行下面的签名生成过程：

（3）消息m 的签名是σ=(j,(e,sj))。

（4）分别更新列表LH和LS。

接下来，如果A 询问H(m,b)，B 检查b=r 是否成立，如果成立返回e ；否则B 选择随机数l ∈，返回lG，并将元组(m,b,lG,l)插入到列表LH中。

密钥泄露查询：A 提交breakin(j+)(1 ≤j+＜N)。若j+≤J ，B报告失败并中止；若j+＞J ，B执行密钥更新算法生成SKj+，即SKj+←Update(…Update(SK0))。B 将SKj+返回给A。

签名查询：A 提交(j,m)(0 ≤j ≤j+) 。B 任意选择k ∈[1 ,n-1] ，计算。然后，将签名( j,(e,sj) )返回给A。

伪造阶段：如果B 在查询阶段没有中止退出，则A将以至少为ε 的优势输出时间段索引j*，消息M*和有效伪造(j*,(e*,sj*))，其中0 ≤j*＜j+。若j*≠J ，则B 报告失败并中止；否则有，那么，从而求得ECDLP问题。

在上述模拟过程中，若B 猜中A 伪造签名的时间段，则在密钥泄露查询时有j+＞J ，即B能产生私钥SKj+而不中止退出，B 猜测正确的概率为1/N ，故B 成功求解ECDLP 问题的概率至少为ε'=ε/N-negl(n)，这里N是时间段总数。

6 效率分析

从算法运算量角度分析，设模乘运算的数据规模是n，1 次倍点运算复杂度是，1 次模逆运算复杂度是（相当于9次倍点运算），1次模乘运算复杂度是。由于改进方案引入了密钥演化思想，和ECDSA方案相比，总体运算效率势必会降低，但是在签名阶段和验证阶段的效率还是很快的。在签名阶段和验证阶段上，将改进方案的运算量与ECDSA 方案的运算量以及同样具有前向安全的周克元方案[11]的运算量进行对比，结果如表1所示。

表1 ECDSA、周克元方案和本文改进方案运算量比较

由表1 可知，在签名阶段和验证阶段，ECDSA 方案的总运算量是N1=O[( 4 lb n+21) n2] ，周克元方案的总运算量是N2=O[( 6 lb n+13 )n2] ，改进方案的总运算量是N3=O[( 2 lb n+2) n2] 。三种复杂度图形表示如图2所示。

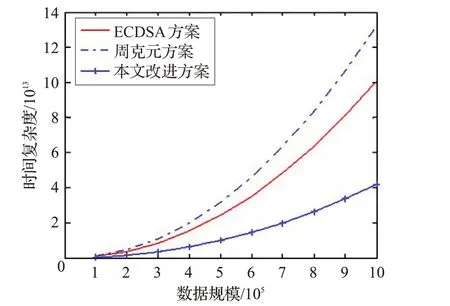
图2 三种方案的签名复杂度比较

本文改进方案在密钥生成上虽然无法和其他两种方案相比，但是它的签名生成和签名验证效率要比其他两种方案高得多。影响复杂度的主要运算是模乘运算和模逆运算，改进方案在签名生成和验证时比ECDSA方案少了2次模逆运算，所以在签名生成和验证阶段改进方案比ECDSA方案的效率高。改进方案和周克元方案同样具有前向安全性，但是与周克元方案相比，改进方案在签名生成和验证阶段少了2 次倍点运算、4 次模乘运算和1次模逆运算，所以改进方案的签名效率提高了很多。因此，与其他两种方案相比，改进方案不仅保证了前向安全性，还大大地提高了签名效率。然而，由于改进方案加入了密钥演化过程，总体效率势必会降低，因此，该方案适用于对安全性要求较高，对总体效率要求低的应用场合。

7 结束语

本文首先对ECDSA 方案进行分析，发现该方案没有前向安全性，存在密钥泄露的安全隐患。针对这个安全隐患，引用徐丹等人[6]的密钥更新方法提出改进方案，并对改进方案进行安全性分析。由分析可知，改进方案可以抗随机数攻击，另外，根据证明可知，在随机预言模型下基于椭圆曲线离散对数问题困难的假设，改进方案满足前向安全性。最后，针对签名过程，运用MATLAB编程将该方案与ECDSA方案以及同样具有前向安全性的周克元方案进行效率比较，发现本文改进方案比其他两种方案的签名效率高。因此，改进方案不仅保证了安全性，签名效率也得到了显著提高。