等截面弹塑性回转体截面翘曲变形分析

刘明君

摘要：研究等截面弹塑性回转体扭转问题，针对不同截面形状，给出了两种求解方法：一种是基于边界方程的半逆解法，另一种是傅里叶解法，两种方法均是通过构造满足控制相容方程的应力函数，反推出截面翘曲位移表达式，可将复杂问题转换为简单问题，并给出具体实例，得到仿真结果图。

关键词：回转体;扭转;翘曲位移

中图分类号：TU313

文献标识码：A

文章编号：1001-5922（2020）12-0121-06

0 引言

等截面回转体的自由扭转是弹性扭转中常见的问题，扭转模型本质上是三维的，通常很难确定解析解[1]。根据Saint Venant原理[2， 3]，在回转体中心位置上，弹性场的特性主要受荷载的合力和合力矩的影响，而荷载的具体分布只影響荷载作用区附近的应力分布，因此在回转体原理末端的位置寻求近似解。从应力函数出发，已有的求解方法包括松弛法，有限元法，非正交曲线查分法等，这些方法均根据三维弹性力学中Kelvin解构造基本解[4-6]。

本文研究等截面弹塑性回转体侧面无外部载荷仅受底端平面受力下的特殊解问题，首先建立回转体基本方程[7]，从相容关系出发，针对椭圆形截面和三角形截面，根据边界条件构造满足条件的应力函数，反推出应变表达式，求解截面翘曲位移。针对矩形截面，将应力函数写成齐次拉普拉斯方程的通解加上非齐次方程特解的形式，并根据标准变量分离法，将齐次解构造成傅里叶余弦级数的形式，反推出截面翘曲位移。以上两种方法都是采用半逆解法推导翘曲位移表达式，使其满足控制方程，将复杂问题转换为简单问题，并最终给出仿真结果图。

1 回转体基本方程

对于如图1所示的等截面弹性回转体，侧面S上无约束，仅在底面R上施加载荷力Q和力矩M，则满足如下条件[8]：

5 翘曲变形求解方法

5.1 基于边界方程的半逆解法

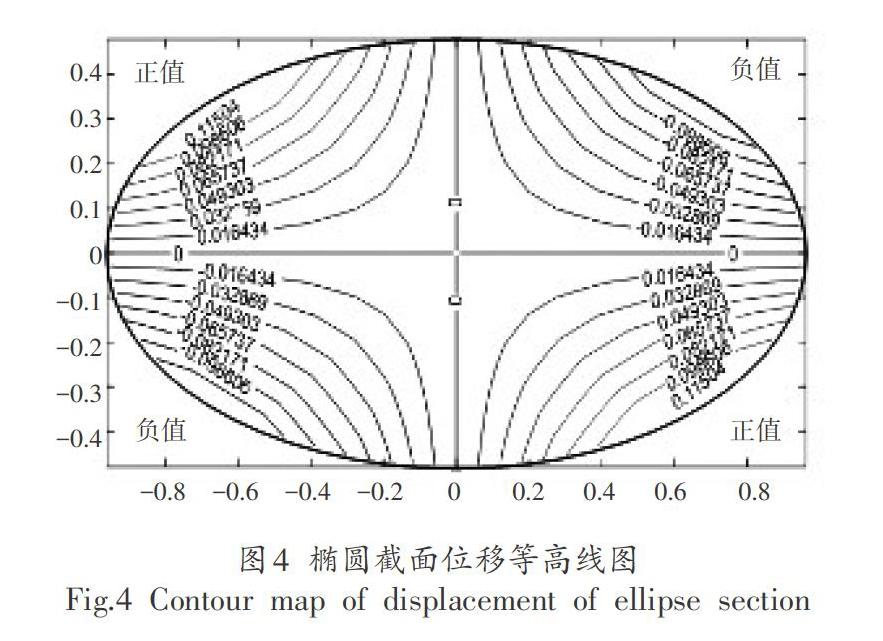
当截面形状为椭圆形时，椭圆的长轴半径为a，短轴半径为b，则边界方程为：

取椭圆的长轴半径为a=1，短轴半径为b=0.5，单位长度扭转角a=1，图4给出了截面位移等高线图，图5为翘曲位移三维图。

图9给出了边长比a/b=1时的截面位移等高线图，对于正方形截面形状，产生了八个位移相似区域，图10为边长比a/b= 0.5时的截面位移等高线图，随着边长比的减小，四个位移区域消失，得到的等高线图类似椭圆截面的位移等高线图。

6 结语

文章给出了等截面弹塑性回转体截面翘曲位移的求解方法，针对椭圆形截面和三角形截面，采用基于边界方程的半逆解法，拟合出满足控制相容方程的直力函数，结合应变方程推导出截面位移变形量;针对矩形截面，无法根据边界方程拟合出满足条件的应力函数，此时采用傅里叶解法，将应力函数分解为齐次和非齐次拉普拉斯方程解之和的形式，根据变量分离法构造傅里叶级数形式的应力函数，满足控制相容方程，最终推导出截面位移变形量。结合实例给出具体推导过程，并进行仿真求解，画出截面位移等高线图。

参考文献

[1]雷小燕，黄茂光，回转体弹塑性扭转问题的一种边界积分方程解法[J].固体力学学报，1985，4（4）：445-455.

[2]梁以德，郑建军，二维弹性平面问题中任意边界条件下应力分布的封闭解[J].应用数学和力学，2007，28（12）：1455-1466.

[3]闰维明，石鲁宁，何浩祥，等，完全弹性支承变截面梁动力特性半解析解[J].振动与冲击，2015，34（14）：76-84.

[4]周凌远，李乔，张士中.采用有限元法计算梁任意形状截面特性[J].计算力学学报，2008，25（5）：634-638.

[5]陈常松，阳斌，颜东煌，任意梁截面特性值的有限元计算方法[J].长沙理工大学学报，2013，10（1）：41-46.

[6]刘佳，崔桐，虚拟等截面弹性柱体自由扭转/变形模型[J].重庆理工大学学报，2012，26（12）：59-64.

[7]路晓明，曹海，龚耀清，任意复杂截面梁的扭转中心[J].力学与实践，2019，41（4）：453-457.

[8] Xianggang Liu， Chuangze Xu， Jiepeng Liu， et al.Re-search on special- shaped concrete- filled steel tubularcolumns under axial compression [J].Journal of Construc-tional Steel Research， 2018， 147 （4）：203-223.

[9]陈明祥，弹塑性力学[M].北京：科学出版社，2010.

[10]杨纲，郝一龙，胡启方，等，任意直角梯形截面梁扭转刚度的无穷级数解法[J].传感技术学报，2012，25（5）：594-598.