基于UKF算法的电池荷电状态SOC估算研究
汤惠淞 吴长水 吴习文

摘 要:新能源汽车锂电池荷电状态是反映电池及电源系统的重要参数,为达到实时估算SOC目的,基于无迹卡尔曼滤波算法提出SOC估算解决方案。在MATLAB/Simulink环境中建立一阶Thevenin等效电路模型和无迹卡尔曼滤波算法,通过建立混合功率脉冲特性实验,辨析出不同SOC和温度对电池模型的影响参数,将辨析出来的参数代入到UKF算法中进行仿真实验。实验结果表明,该荷电状态估算具有较高的精准度。
关键词:荷电状态;无迹卡尔曼滤波;等效模型电路;混合脉冲功率特性;汽车电子
DOI:10. 11907/rjdk. 201337 开放科学(资源服务)标识码(OSID):
中图分类号:TP301 文献标识码:A 文章编号:1672-7800(2020)011-0090-06
SOC Estimation of Battery State of Charge Based on UKF Algorithm
TANG Hui-song,WU Chang-shui,WU Xi-wen
(College of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China)
Abstract: The state of charge (SOC) of lithium battery in new energy vehicle is an important parameter reflecting the battery and power system. In order to estimate SOC in real time, this paper proposes a solution based on Unscented Kalman filter (UKF) algorithm. In Matlab / Simulink environment, the first-order Thevenin equivalent circuit model and unscented Kalman filter algorithm are established. Through the establishment of mixed power pulse characteristics experiment, the influence parameters of different SOC and temperature on the battery model are distinguished. Finally, the discriminated parameters are put into UKF Algorithm for simulation. The simulation results show that the state of charge estimation developed in this paper has high accuracy.
Key Words: state of charge; unscented Kalman filter algorithm; equivalent circuit model; hybrid pulse power characteristic; automotive electronics
0 引言
電池荷电状态(State of Charge,SOC)代表电池当前的剩余电量,决定当前状态下汽车可续驶里程。由于控制策略本质上依赖SOC估计,电池管理系统(BMS)可依据当前的剩余电量对电池充放电过程进行调整。所以,SOC时刻影响电池的充电效率和整车输出动力。郑旭等[1]、欧阳北平[2]对SOC估算结果受温度、电池健康状态、充放电流大小、传感器测量精度等影响因素进行研究,但该结果不能直接测量,必须通过电池模型参数估计。
SOC估计方法研究较多,如鲍慧等[3] 研究安时积分法估算SOC的误差校正;杨光荣等[4]改进安时积分法估算SOC;王党树等[5]设计扩展卡尔曼滤波(Extended Kalman Filter,EKF)的锂电池SOC估计;李泽洋等[6]、邹焕尧等[7]、杨峰等[8]、高凯等[9]基于UKF方法估算锂电池SOC。
虽然估算SOC方式很多,但是不同的方法有不同的局限性。安时积分法是应用最广泛的SOC估计方法,但需要高精度的电流传感器和准确的初始SOC值,累积误差和不确定干扰易造成估计精度不高。EKF算法需要计算雅可比矩阵,对于嵌入式芯片计算负担较大。本文综合以上方法开发新的UKF算法,通过建立精确表征电池充放电过程的等效电路模型,从中提取能唯一确定的模型参数。然后通过实验对未知参数进行辨析,将辨析的结果作为已知参数。将待估量非线性函数转化为待估量概率函数代入到UKF算法中,对该参数不断更新与估算。通过仿真对比真实的SOC和估算的SOC,发现本文UKF算法具有较高精度。
1 电池模型構建与参数辨析
锂电池作为一个非线性系统,其充放电过程很复杂,为方便研究,采用等效电路模型精确模拟电池在充放电时的电化学过程。通过实验与计算辨析出等效电路中电阻、电容、电压源的变化情况,从辨析过程展现电池内部参数。通过混合脉冲功率(Hybrid Pulse Power Characteristic,HPPC)实验方法,结合数学求解微分方程辨析出电池内部机理参数[10-12]。在实验过程中采用控制变量法,通过改变环境温度、SOC值和充放电倍率等,得到不同条件下的电池模型参数,并建立各种影响因素与电池参数的对照关系表。在当前电流、温度、电压等状态下[13-14]查找对照关系表就能得到当前状态对应的电池参数,再通过UKF算法计算得到电池的SOC估算结果。
1.1 等效电池模型建立
下面介绍常见的等效电路模型。
1.1.1 Rint内阻电路模型
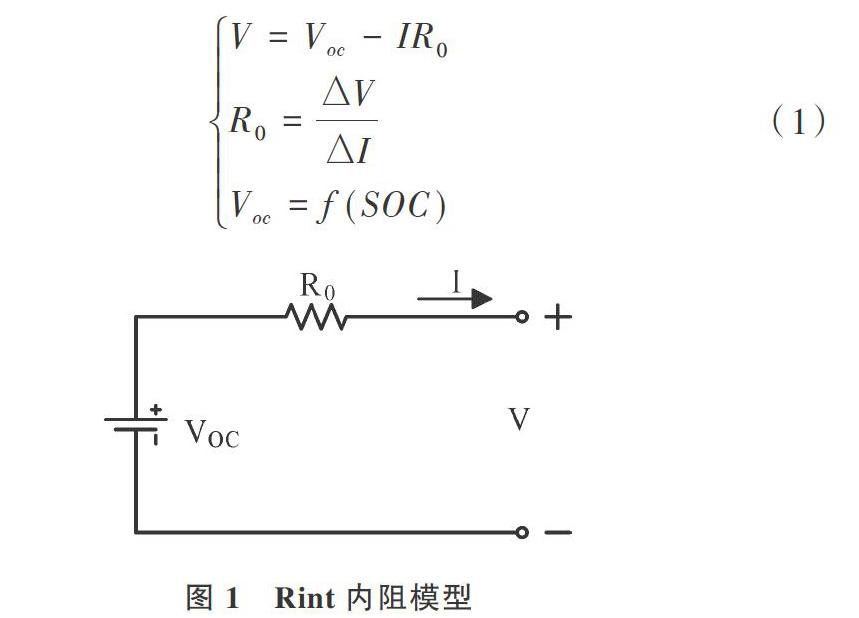
Rint内阻电路模型如图1所示。电阻R0完全表征电池的欧姆内阻和极化内阻,用VOC表示电池开路电压,用V表征实时测量的电池端电压。由于电阻R0并不能真实反映电池内部极化效应,故估计时存在较大误差,所以使用Rint模型获得SOC估计精度很低。
Rint内阻等效电路模型公式如下:
V=Voc-IR0R0=?V?IVoc=f(SOC) (1)
1.1.2 一阶Thevenin电路模型
一阶Thevenin电路模型如图2所示。相比于Rint内阻模型,为了表征电池充放电过程中的极化效应,Thevenin模型增加一个RC并联电路。R1表示极化内阻,C1表示极化电容。该模型能较好地表征电池的内部特性,具有精度较高、计算量小等特点。
Thevenin等效电路模型公式如下:
V=Voc-IR0-V1I=V1R1+C1dV1dt (2)
1.1.3 多阶RC电路模型
多阶RC电路模型如图3所示。该模型采用多阶RC并联电路,可精确表征电池内部电化学过程,但是RC的阶数对计算过程要求很高,对处理芯片的计算能力要求高。
多阶RC等效电路模型公式如下:
V=Voc-IR0-V1-?VnI=V1R1+C1dV1dt=?=VnRn+CndVndt (3)
一阶Thevenin电路模型能够完整体现电池内部电化学变化过程,精度较高,模型推导公式复杂度较小,对处理芯片运算能力要求较低,所以本文采用一阶Thevenin电路模型作为研究对象进行设计[15-17]。
1.2 HPPC测试实验
为进一步分析电池在不同SOC和温度条件下模型参数变化情况,本文采用脉冲电流激励促使电池端电压变化,从而分析电池内部的变化情况。
HPPC测试过程:为保证测量数据的有效性,采用控制变量法,将电池放置在恒温恒湿环境中,如在10℃恒温下,将电芯SOC调整到90%,以10C脉冲电流放电10s,再静止40s,然后以10C电流充电10s。这样一个循环完成在特定温度下SOC为90%的HPPC测试。然后调整SOC以1C放电至80%,在该状态下进行HPPC测试。重复多次实验并改变SOC值,完成不同SOC下的HPPC测试,并时刻记录单体电池电压、电流、温度和放电量随脉冲电流和时间的响应情况。图4为恒温10℃时,SOC从90%到60%的HPPC测试曲线。
为更好地体现单体电池电压变化曲线,随机选取图4中的某特定温度和SOC状态下的HPPC测试结果进行放大,如图5所示。
上述测试过程完成温度为10℃、SOC从90%到10%的HPPC测试。采用同样方式,测试SOC在-20℃、-10℃、0℃、10℃、20℃、30℃、50℃不同温度环境下的变化情况,并记录每一组HPPC测试数据。最后将测得的HPPC数据进行参数辨析,得到不同温度和SOC状态下的Thevenin电池模型参数。
1.3 等效电路模型参数离线辨析
根据以上测得的HPPC实验结果进行电池等效电路模型参数辨析。图5为某一特定温度、特定SOC值下的HPPC脉冲测试单体电池电压响应图。随着脉冲放电、充电电流的开启和结束,单体电池的电压变化趋势也表现出下降和上升变化。
对图5中HPPC曲线走向进行分析。激励放电电流在欧姆内阻作用下,V1~V2和V3~V4两个阶段都出现电压骤变。为减少测量误差,R0值为两阶段中阻值的平均值,由此计算出Thevenin模型中欧姆内阻R0阻值,计算公式如下:
R0'=?V?I=V1-V2IR0''=?V?I=V4-V3IR0=R0'+R0''2 (4)
由V2到V3电压呈曲线缓慢下降趋势,原因是极化电容放电产生的零输入响应,由此得到响应方程为:
V3=V1(1-et3τ)V4=V1(1-et4τ) (5)
式(5)中τ为Thevenin电路模型中的阻容时间常数,存在如下关系式:
τ=R1C1 (6)
结合式(5)和式(6),求解出时间常数如下:
τ=-t4-t3ln(V1-V4V1-V3) (7)
V4~V5阶段电压曲线上升,是因为当放电电流消失后,极化电容产生零输入响应,响应方程为:
VRC=IR1(1-etτ)V3=VOC+IR0+VRC (8)
式(8)中,VRC为Thevenin模型中极化电容两端电压,将式(7)代入式(8),由此求出极化内阻R1、C1:
R1=V3-VOC-IR0I(1-et2-t1τ) (9)
C1=τR1 (10)
建立Thevenin电路模型中的R0、R1、C1等参数,可通过HPPC测试结果和辨析过程计算出来。在不同温度、不同SOC下,得到的参数结果是不同的,如表1所示。表1显示在恒温20℃、不同SOC下的辨析结果。
2 基于UKF的SOC估算
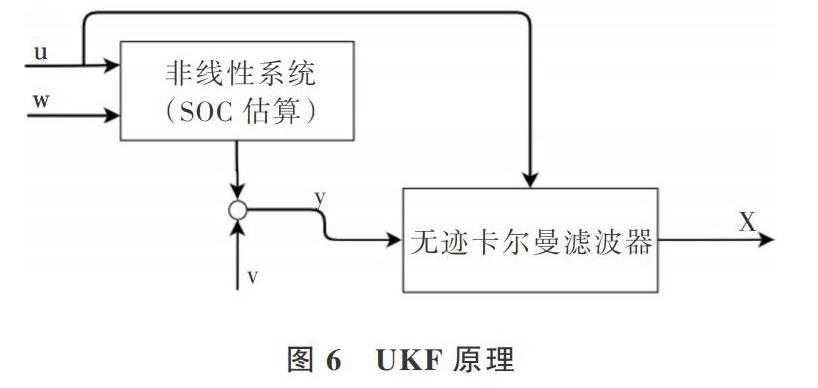
将等效电池模型辨析参数代入UKF[12]算法中,通过算法设计实现SOC估算。UKF原理如图6所示。
图6中,w为过程噪声,v为测量噪声,u为输入量,即为传感器所测得的单体电池端电压;y为非线性系统输出量,即为单体电池开路电压;x为UKF估算SOC结果。
2.1 UKF狀态方程和测量方程
设计UKF算法的关键技术是确定UKF状态转移方程和测量方程。在等效电路模型参数辨析结果基础上可通过查表得出不同温度和SOC下的R1、C1、R0、VOC值。动力电池模型是一个高度非线性系统,设该系统状态向量为χT,其包含两个状态参数SOCT和U1T,则系统状态向量为:
xT=SOCTU1T (11)
由电池模型可知电池系统状态转移方程如下:
??tSOCU1=0-U1R1(SOC,Tb)?C1(SOC,Tb)+-13600?Cq1C1(SOC,Tb)I+W (12)
式中,R1、C1为Thevenin电池模型中阻容电路的阻值和电容值,Tb为单体电池温度,U1为极化电容C1的端电压,Cq为电池容量。
无迹卡尔曼滤波器为离散型滤波器,使用欧拉公式对系统状态转移方程进行离散化。离散化后的非线性系统状态转移方程可简单描述为:
XT+1=XT+f(XT,UT)Ts (13)
式中,TS为采样时间。运用欧拉公式对状态转移方程离散化,得到的转移方程为:
SOCT+1U1T+1=SOCTU1T+-I3600?Cq-U1R1(SOCT,Tb)?C1(SOCT,Tb)+IC1(SOCT,Tb)TS+WT (14)
状态转移方程的Simulink模型如图7所示,用一个Simulink函数表征本文电池系统状态转移方程。
根据Thevenin电路模型,电池系统测量方程为
E=VOC-U1-IR0(SOC,Tb)+V (15)
式中,E为测量所得端电压,V为测量噪声。电池系统测量方程的Simulink模型[18]如图8所示,使用模块函数表征本文电池系统测量方程。
2.2 UKF运用
UKF算法可将系统状态量的非线性函数转化为非线性概率密度函数,生成多个散布在状态量均值附近的点,所生成的均值和协方差与非线性函数状态量的均值和方差是等同的,称所形成的点为Sigma点。在UKF状态方程和测量方程中,Sigma点作为输入量,将Sigma点的非线性变换获得的新状态点和测量值作为下一时刻的状态估计值和协方差输入量。在更新和估算过程中,状态量的均值和协方差能达到泰勒计数的四阶精度。通常将UKF算法分为初始化、预测和更新3个阶段进行分析。
2.2.1 初始化阶段
本文状态量为XT,包含SOCT和U1T两个状态参数,XT初始化为:
xT=ExT (16)
进行误差协方差矩阵P0的初始化:
P0=E(xT-xT)(xT-xT)T (17)
2.2.2 预测阶段
在第k时刻到来时对SOC和SOC的误差方差矩阵作预测,其中χk-1为Sigma点的矩阵并满足
χk-1=Ak-1χi,k-1+Bk-1uk-1xk=i=02nωmiχi,k-1*P-x,k=i=02nωciχi,k-1*-xkχi,k-1*-xkT+Qk (18)
2.2.3 更新阶段
对第k时刻的单体电池端电压进行估算:
yi,k-1*=Ck-1χi,k-1*+Dk-1uk-1yk=i=02nωmiyi,k-1* (19)
对第k时刻测量所得的单体电池端电压的方差矩阵进行计算:
Pyy=i=02nωciyi,k-1*-ykyi,k-1*-ykT+Rk (20)
对第k时刻的SOC与测量所得端电压的协方差进行计算:
Pxy=i=02nωciχi,k-1*-xkyi,k-1*-ykT (21)
计算卡尔曼滤波增益:
Kk=PxyPyy (22)
UKF算法工作过程是依据电池模型辨析的参数计算得到当前状态下的开路电压。由OCV-SOC得到SOC的初级预估,然后将SOC作为输入量代入到UKF算法中,进行SOC更新和修正,最后得到SOC估算值。通过修正UKF使估算結果接近测量的真实端电压,提高估算精度。图9为OCV-SOC曲线,图10为UKF估算策略。
3 软件仿真验证
在Simulink中用辨析参数搭建Thevenin电池仿真模型,保证仿真模型和实际电池的参数匹配,如图10所示。电池模型能根据输入的充放电电流产生仿真温度、端电压和SOC。通过对电池模型施加充放电电流激励信号,可得到对应的SOC与端电压输出。根据电池实际使用特点,充电激励信号采用恒流15A,而放电激励电流采用随机信号模拟整车真实的电池放电过程。电池模型充放电电流信号如图11所示。
将状态转移方程和测量方程代入到UKF算法中,并将电池模型的参数导入到电池模型中,通过不断模拟充放电过程实时改变电池的SOC。电池模型会输出一个真实的SOC,将真实的SOC和无迹卡尔曼滤波器估算所得SOC进行比较,如图12所示。从图中可知,在初始估算时,UKF并不能准确得到SOC的初始值,所以初始估算结果存在较大误差。为解决这一问题,采用开路电压法求得精确的SOC初始值作为UKF初始值。整个过程仿真误差如图13所示。
由图13可知,无迹卡尔曼滤波器的初始瞬间估算误差达到13%,而后期随着估算过程收敛,误差基本保持在3%以内,证明本文所选的无迹卡尔曼滤波器具备较高精度,实用价值高。电池模型的参数辨析结果需要代入到无迹卡尔曼滤波器中,从侧面证明了本文参数辨析结果精度较高。
4 结语
本文通过对比不同等效电路模型的精度和复杂度,确定并建立了Thevenin等效电路模型,用于描述动力电池充放电过程的电化学机理。在不同温度与SOC状态下进行HPPC实验,通过分析HPPC实验结果,完成不同温度和不同SOC下电池模型参数的离线辨析。详细阐述了UKF原理,根据建立的Thevenin等效电路模型确立UKF状态转移方程和测量方程,将电池模型参数代入到UKF中设计UKF算法。对开发软件进行了仿真验证。后续可在验证软件功能的同时进行硬件在环测试,以完整验证软件在控制器中运行效果。未来还可将SOC估算的Simulink应用层软件转化为符合AUTOSAR架构规范的软件组件,以提高软件可移植性。
参考文献:
[1] 郑旭,黄鸿,郭汾. 动力电池 SOC 估算复杂方法综述[J]. 电子技术应用,2018,44(3):3-6,10.
[2] 欧阳北平. 电动汽车锂离子动力电池SOC预估系统[D]. 天津:天津工业大学,2019.
[3] 鲍慧,于洋. 基于安时积分法的电池SOC估算误差校正[J]. 计算机仿真,2013,30(11):148-151,159.
[4] 杨光荣,朱赛飞,陈阳,等. 基于改进安时积分法估计锂离子电池组SOC[J]. 电源技术,2018,33(9):59-63.
[5] 王党树,王新霞. 基于扩展卡尔曼滤波的锂电池SOC估算[J]. 电源技术,2019,43(9):1458-1460.
[6] 李泽洋,李振强,吕丰. 基于UKF方法的锂离子电池荷电状态估计研究[J]. 广西科技大学学报,2019,55(8):134-139.
[7] 邹焕尧,王宏朋,黄凯. 基于无迹卡尔曼滤波算法的锂电池SOC估计[J]. 汽车使用技术,2018,24(19):22-24.
[8] 杨峰,郑丽涛,王家琦,等. 双层无迹卡尔曼滤波[J]. 自动化学报,2019,45(7):1386-1391.
[9] 高凯,高军,张勇. UKF在估算锂电池SOC中的应用[J]. 中国科技信息,2019,55(14):63-64,66.
[10] 易鸿. 基于EKF-UKF模型的锂电池电源参数更新和估计[J]. 西华大学学报(自然科学版), 2019,38(2):103-107.
[11] HU X, LI S, PENG H. A comparative study of equivalent circuit models for li-ion batteries[J]. Journal of Power Sources, 2012,198(3):359-367.
[12] HU X, LI S, PENG H. A comparative study of equivalent circuit models for li-ion batteries[J]. Journal of Power Sources,2012,198(1):359-367.
[13] 胡小军. 基于无迹卡尔曼滤波的动力锂电池SOC估计与实现[D]. 长沙:中南大学,2014.
[14] 胡志坤, 刘斌, 林勇, 等. 电池 SOC 的自适应平方根无迹卡尔曼滤波估计算法[J]. 电机与控制学报, 2014, 18(4):111-116.
[15] 徐颖, 沈英. 基于改进卡尔曼滤波的电池 SOC 估算[J]. 北京航空航天大学学报, 2014, 40(6): 855-860.
[16] AUNG H,LOW K S,SHU T G. State-of-charge estimation of lithium-ion battery using square root spherical unscented kalman filter (sqrt-ukfst) in nanosatellite[J]. IEEE Transactions on Power Electronics, 2015(30):4774-4783.
[17] ZHANG J,XIA C. State-of-charge estimation of valve regulated lead acid battery based on multi-state unscented kalman filter[J]. International Journal of Electrical Power & Energy Systems, 2011 (33): 472-476.
[18] 杨刘倩,詹昌辉,卢雪梅. 基于MATLAB的锂电池健康状态建模实现[J]. 计算机仿真,2015,32(7):121-124.
(责任编辑:杜能钢)

