融合Elman神经网络与EMD的交通拥堵指数预测
李振国 徐建新

摘 要:为了提高传统方法生成交通拥堵指数(TPI)的准确率,引入一种基于经验模态分解(EMD)与Elman神经网络的组合模型实现交通拥堵指数预测。首先,利用EMD将TPI序列分解为不同时间尺度下的IMF分量和剩余分量;然后,通过偏自相关函数(PACF)计算各分量的滞后期数,以此确定各分量在Elman神经网络中的输入和输出变量;之后,通过上述方法计算出各分量预测值并相加;最后,计算出总预测结果。通过计算结果可知,EMD-PACF-Elman预测方法3个评价指标(平均绝对误差、均方误差、平均绝对百分误差)的计算结果与单一Elman神经网络模型、EMD-Elman神经网络模型、单一BP神经网络模型、EMD-BP神经网络模型相比都为最低,分别为0.562 4、0.598 9、0.110 7。因此, EMD-PACF-Elman预测方法可以有效地预测TPI,同时也为进一步预测交通拥堵趋势提供了依据。
关键词:经验模态分解;偏自相关函数;Elman神经网络;交通拥堵指数
DOI:10. 11907/rjdk. 201977 开放科学(资源服务)标识码(OSID):
中图分类号:TP301 文献标识码:A 文章编号:1672-7800(2020)011-0011-06
Prediction of TPI Based on Elman Neural Network and EMD
LI Zhen-guo1,XU Jian-xin 2
(1. Faculty of Science, Kunming University of Science and Technology, Kunming 650500, China;
2. School of Metallurgy and Energy Engineering, Kunming University of Science and Technology, Kunming 650093, China)
Abstract:In order to improve the accuracy of generating traffic performance index (TPI) by traditional methods, a combined model based on (EMD) and Elman neural network is introduced to predict the traffic performance index. First, EMD is applied to decompose the sequence of TPI into IMF component and residual component on different time scales; second, partial autocorrelation function (PACF) is used to calculate the lag period of each component and the input and output variables of each component in Elman neural network are determined; third, the predicted values of each component are obtained and the final prediction result is obtained by summing them together. According to the results, the three evaluation indexes (mean square error, mean absolute error and mean absolute percentage error) of EMD-PACF-Elman prediction method are the lowest compared with single Elman neural network model, EMD-Elman neural network model, single BP neural network model and EMD-BP neural network model, and they are 0.562 4, 0.598 9 and 0.110 7 respectively. EMD-PACF-Elman prediction method can effectively predict TPI. It also provides an effective basis for further predicting the trend of traffic congestion.
Key Words:EMD; PACF; Elman; traffic performance index
0 引言
城市交通擁堵是一个困扰全球的问题,其会导致交通效率降低、交通事故发生率提高等问题。目前,在智能交通系统中,交通拥堵预测在道路引导以及交通管理中都发挥着重要作用,因而受到越来越多学者的关注[1]。交通拥堵指数(Traffic Performance Index,TPI)可以直接反映当时的道路交通状况,因此本文通过预测交通拥挤指数判断交通状态。
许多学者对短期交通流预测进行了研究与探索[2-4],提出了多种预测方法,如线性预测方法及非线性预测方法。其中,线性预测方法包括多元线性回归方法[5]、状态空间方法以及时间序列方法[6]等。但这些方法只能描述交通流基本趋势,而不能对其进行准确预测;非线性预测方法包括灰色模型法[7-8]、贝叶斯网络法、神经网络法[9]、小波模型法[10]以及RBF网模型法等。
国内外学者在预测TPI序列时尝试了多种方法,如静态前馈神经网络[11],但该方法有一定弊端,当系统的阶数变化或未知时,在运算过程中会导致网络学习的收敛速度变得十分缓慢,此时很容易陷入局部极小值。动态回归神经网络有效改善了这一问题,其可以非常形象、直观地反映系统的动态特性,以便于观察。Elman神经网络其实是一种非常有代表性的动态回归神经网络[12-13],考虑到TPI数据序列的动态和非线性特性,Elman网络可用于预测。但从以往的研究来看,网络模型能够很好地预测趋势,但预测值的准确性不高。
近年来,常常看到小波分析被应用于信号处理中,其优点是克服了人工选择的局限性,但在处理非线性问题时,对于小波母函数和分解层数的选择没有提供完善的理论支持。经验模态分解(EMD)的一个重要优点就是可避免人为因素造成的较大误差,因此是一种有效的时变信号信息提取工具,具有自适应非线性特征。同时,EMD能准确反映一些有价值的物理信息,尤其对于非平稳信号处理具有更佳的效果。它可以将非平穩、非线性的交通拥堵指数(TPI)序列分解成多个平稳的线性本征模态函数(IMF)和剩余分量,然后对分解后的每个分量分别进行建模,既能准确预测TPI的趋势,又能提高预测值的准确性。因此,对TPI的研究可以转化为对各个分量的研究。
本文选取TPI序列检验其稳定性和正态性,结果是一个非平稳、非线性序列。将处理时频信号的EMD与Elman神经网络相结合,可提高Elman神经网络预测TPI的准确性。首先,EMD将TPI序列分解为多个IMF分量和剩余分量;然后,分别确认各分量的滞后期数,利用偏自相关函数 (PACF),通过计算出的各分量滞后期数确定网络的输入和输出变量;之后,分别对各个分量进行建模,组成EMD-PACF-Elman组合模型预测分解后的TPI序列;最后,将分解后的各分量预测值全部相加,得到最终预测值。通过对比分析可知,本文引入的模型可以很好地预测道路交通状况,得出的结果具有较高准确性。
1 数学原理与方法
1.1 Elman神经网络
Elman神经网络在1990年被提出,是一种典型的局部回归网络。其主要框架为前馈链接,包含3个层次,即输入层、隐含层和输出层[14]。利用Elman神经网络可获得较好的TPI预测结果。Elman神经网络表达式为:
式中,[u(k)]表示输入向量,[x(k)]、[xc(k)]、[y(k)]表示输出向量,k表示时刻值,下标c对应隐含层个数,[w1]、[w2]、[w3]对应连接权值,f对应隐含层神经元传递函数,g则对应输出神经元传递函数,不能忽略。
1.2 EMD原理
EMD是Huang等[15]提出的一种基于“筛选”的方法,其主要思想是将不稳定信号分解为相对稳定且有限个IMF分量和剩余分量。其实质是将TPI原始数据分解成多个IMF分量和剩余分量,其中每个IMF分量都包含了原始数据对应时间段的原有特征。
EMD方法实现步骤如下:
步骤1:需要准确找到TPI序列[xt] ([t=1, 2, ……, T])的局部极值点,然后根据计算得到的极值点进行三次样条插值,从而确定计算上、下包络序列[xmaxt, xmint]。
步骤2:从确定的上、下包络序列得到平均曲线序列,其数学表达式为:
步骤3:用TPI序列[x(t)]减去步骤2所得的平均曲线序列后得到一个新的时间序列。通过去除平均曲线序列,可得到数据的其余分量。即:
步骤4:对计算出的新的时间序列[h1(t)]重复以上步骤,循环依次计算,一直计算到新的时间序列满足以下两个特定条件:①局部极值点以及过零点数目必须等同,或最多相差一个;②每一个瞬时平均值为零,直到满足且达到以上两个特定条件后,则新的时间序列[h1(t)]就是第1个IMF分量[IMF1]。
步骤5:用交通拥堵指数序列[xt]减去[IMF1],得到剩余分量[r1t]。
步骤6:重复上述步骤1-5,计算剩余序列,可得到多个IMF,一直计算到满足终止条件。
当[i=1, 2, ……n], [t=1, 2, ……, T],[T]是时间序列长度,[ i]是迭代次数,[ σ]是停止阈值,[ σ]取值范围为[0.2,0.3],重复迭代n次,直到剩余序列可以不再被分解,该剩余序列被称为剩余分量[Rt],然后TPI序列可表示为:
步骤7:重复步骤1-6。
1.3 偏自相关函数
偏自相关函数(Partial Autocorrelation Function,PACF)是一种用来识别ARMA(p,q)中p的常用方法,p为滞后阶数,在运算过程中剔除中间变量的影响后,可以更加直观地反映出时间序列中任意两个变量之间的相关性。本文采用偏自相关函数方法确定各分量的滞后阶数,通过该方法确定Elman神经网络的输入和输出变量16]。
1.4 EMD-PACF-Elman神经网络预测模型
本文引入新的EMD-PACF-Elman预测模型,具体预测流程如图1所示。
首先,利用EMD对交通拥堵指数数据进行处理,该处理方法可将TPI原始序列分解为多个IMF分量和剩余分量。然后,通过使用偏自相关函数(PACF)方法求出各分量的滞后阶数,通过计算出的滞后期数分别确定子模型中神经网络的输入和输出变量。之后,建立各分量EMD-PACF-Elman联立的新组合神经网络模型,通过使用新的组合模型分别依次计算出各分量预测值。最后,将所有计算出的各子模型预测结果全部相加,所得到的和即为最终预测结果。具体步骤如下:
步骤1:设[x(t)] ([t=1,2,……])为交通拥堵指数序列,将[x(t)]序列进行EMD分解,通过分解计算得到8个[IMFj]分量([j =1, 2, ..., 8])和1个剩余分量[R(t)]。
步骤2:使用偏自相关函数方法分别确定每一个IMF分量以及剩余分量R(t)的滞后阶数,首先计算滞后阶数的结果,进一步确定每一个子模型的输入变量,然后通过计算与反复训练,以此确定隐含层神经元数量,最后确定模型的输出变量。
步骤3:将交通拥堵指数原始数据样本分为3个样本集,分别为训练集、测试集及预测集。首先,将训练集样本用于组合预测模型之前,目的是为了训练参数,使预测集可以达到正常的预测效果。测试集的作用是测试网络预测效能,在实际运算过程中,对预测集样本进行预测,从而得到预测模型的预测样本。
步骤4:重复步骤2和步骤3,分别得到其它分量和剩余分量的预测结果。
步骤5:将每个IMF分量与剩余分量的预测结果相加,所得结果就是TPI的最终预测结果。
2 结果与讨论
2.1 样本数据描述与预处理
交通状况指数(TPI记录时间为2015年1月1日-2019年5月31日),所有数据均来自广州交通信息网(http://jtj.gz.gov.cn/jtzt/jtsj/xyglsj/),共有1 145个有效樣本集作为研究对象。
本文采用Windows7系统平台,TPI(2015年1月1日-2019年5月31日)的原始数据图如图2所示。交通拥堵指数序列呈非线性特征,同时具有较大的波动性,但也具有一定趋势性。但是,图2中并没有清晰、明确地显示出规律性,若想对其进行准确预测存在较大困难。因此,本文采用EMD-PACF-Elman方法对选取的数据进行预测,并分别与不使用EMD的Elman方法(Elman单一模型)、EMD-Elman模型、BP单一模型和EMD-BP模型进行比较。
2.2 EMD输入模型训练
采用EMD方法分解TPI原始序列得到的分解结果如图3、图4所示。从图中可以很容易看出,经过分解共得到8个IMF分量以及1个剩余分量[Rt]。
在网络训练与预测过程中,权值和阈值是由随机数随机选取的,因此权值与阈值选取也十分重要。网络收敛速度自然会随着每次运行而变化。经过反复比较,权值初始取值范围选取(-0.1,0.1)较优。
在神经网络中,最关键的步骤之一就是模型参数设置,其在模型中起着决定性作用。参数调试中最重要的两个量,一是输入层的神经元数量,二是隐含层的节点数量,模型建立是否成功的关键也在于此。对时间序列数据建立Elman神经网络模型时,输入层神经元数量通常对模型预测性能有着重要影响,模型的输入层神经元数目通常由时间序列的滞后期数决定。因此,计算时间序列的滞后周期是非常重要的。
目前常用于计算时间序列滞后周期的方法之一是PACF法,因此本研究使用PACF确定TPI序列的滞后周期。首先,通过EMD方法得到IMF分量和剩余分量[Rt],然后计算其滞后期,最后以滞后期数作为对应Elman神经网络子模型的输入层神经元数。TPI序列滞后周期计算结果如表1所示。
隐层节点数同样是重要参数,但目前还没有具体计算标准,大多数情况下是根据经验设置隐含层节点个数。本文将每个模型隐含层神经元数量范围确定为相应输入神经元数量的75%~300%,并对新预测模型反复进行训练对比,通过比较网络误差,以此确定隐层神经元最优数目,最终确定TPI各子模型的隐含层神经元数量。
2.3 EMD-PACF-Elman神经网络预测效果
本文选取TPI的1 145个有效样本集作为研究对象,选取T的1 100个数据作为训练数据,建立EMD-PACF-Elman神经网络预测模型,共使用40个TPI的有效数据作为检验数据进行模型检验。
由于每个子模型输入变量不同,导致每个子模型输出变量也不同。为了保证各子模型输出变量的矢量长度相同,从而较好地获得最终预测值,删除子模型的部分输出变量。
为了更准确地观察数据处理结果,通常对以下3个误差指标进行分析,从而判断预测效果,分别是:均方误差(MSE)、平均绝对误差(MAE)以及平均绝对百分比误差(MAPE)。利用EMD-PACF-Elman神经网络对每个IMF和剩余分量进行训练与建模。TPI各分量预测误差如表2所示。
3个误差评价指标计算公式如下:
其中,[yt]代表TPI实际值,[yt]代表了TPI预测值。
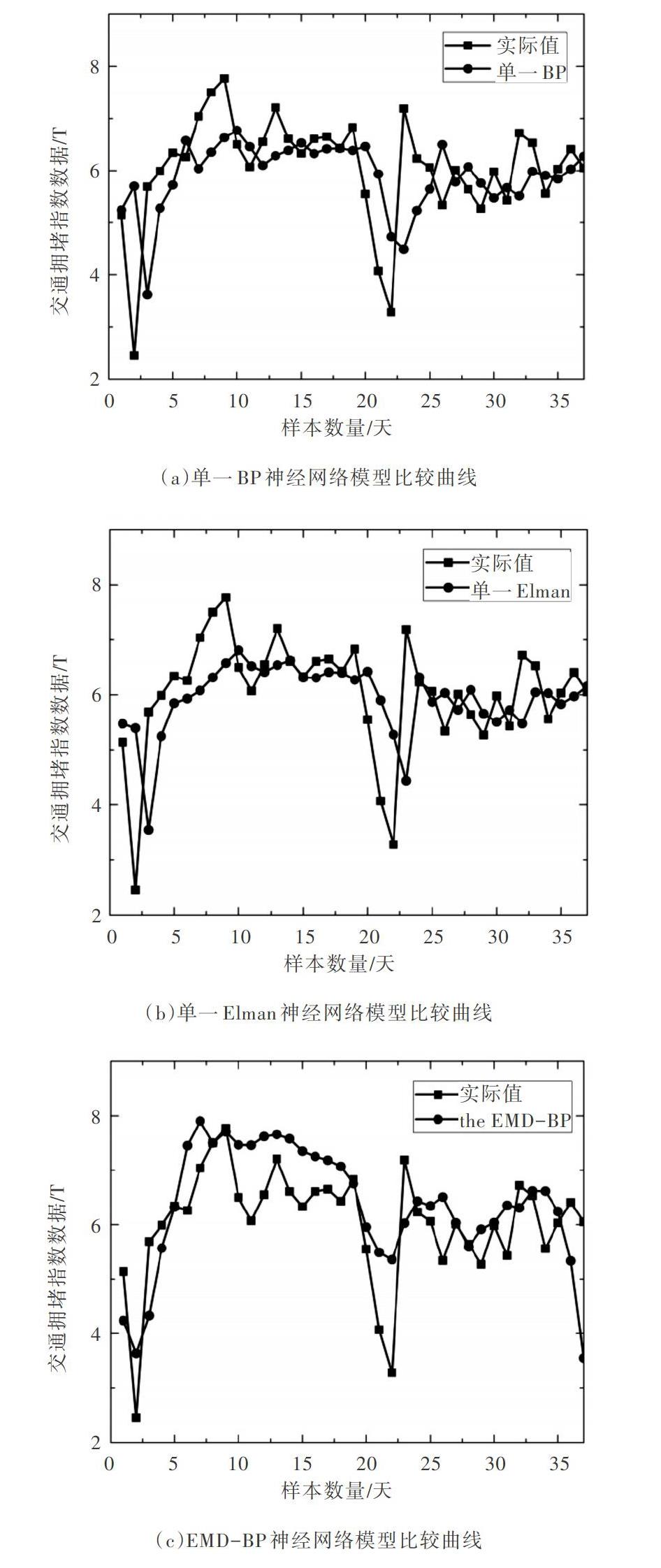
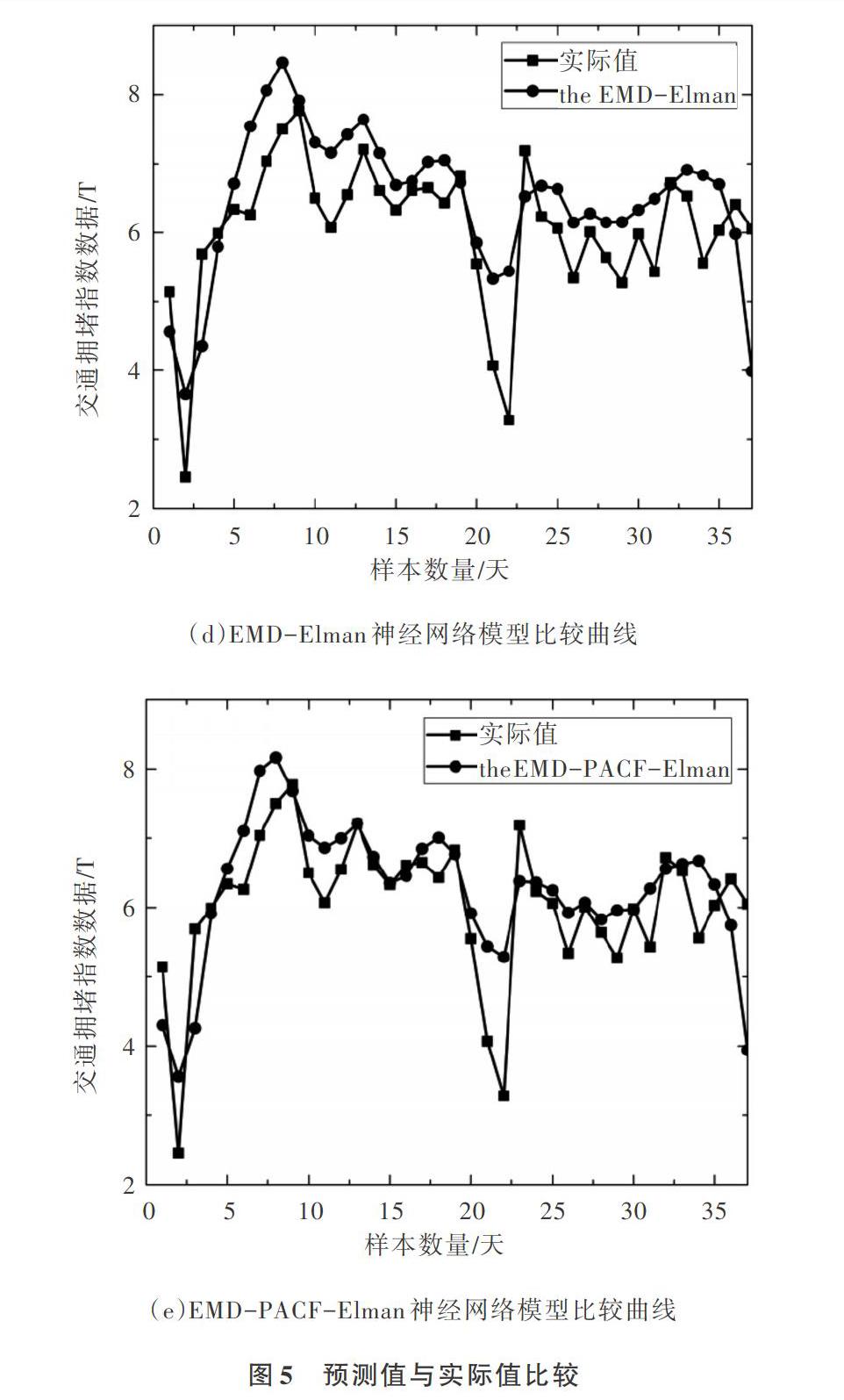
本文对交通拥挤指数进行研究(周六和周日不考虑),连续5天的数据可用来对第6天进行预测,因此将Elman神经网络子模型的输入变量设置为5。为了区分本文使用PACF确定各子模型输入变量的方法,将该方法称为EMD-Elman模型。为了更直观地观察EMD-PACF-Elman模型预测情况,把EMD-PACF-Elman模型预测结果分别与单一BP神经网络模型、单一Elman神经网络模型、EMD-BP神经网络模型和EMD-Elman神经网络模型预测结果进行对比。预测与实测TPI结果比较曲线如图5所示。
2.4 结果分析
如图5(e)所示,单用肉眼很难分辨出EMD-PACF-Elman神经网络模型的最高预测精度。为进一步说明EMD-PACF-Elman神经网络的性能,选取MAE、MSE和MAPE作为误差指标进行分析判断,如表3所示。通过EMD-PACF-Elman神经网络得到MAE、MSE和MAPE的结果分别为0.562 4、0.598 9、0.110 7,明显低于其它4组模型的结果。该结果表明,EMD-PACF-Elman神经网络模型的预测精度较高。
通过上述比较,本文引入的神经网络模型实现了对TPI的准确预测,具有一定的实际应用价值。
3 结语
本研究首先通过EMD方法将TPI原始数据分解为多个平稳、线性的IMF分量和剩余分量;然后使用PACF方法依次确定Elman神经网络的输入与输出变量,进而建立每个分量的EMD-PACF-Elman组合子模型;最后将每个分量子模型的预测结果相加,并将得到的预测结果分别与单一BP、单一Elman、EMD-BP和EMD-Elman神经网络模型进行比較分析。通过使用3个误差评价指标进行分析判断,得到EMD-PACF-Elman组合模型的TPI预测值与实际值之间的误差分别为0.562 4、0.598 9、0.110 7。根据3个误差指标,显示EMD-PACF-Elman组合模型的预测精度高于其它4种方法,证明了该方法的有效性。该方法为进一步预测交通拥堵趋势提供了有效依据。然而,该方法所得出的误差值相对偏大,预测还存在一定偏差,此外该方法的普适性还需作进一步验证,这些都是下一步需要解决的问题。
参考文献:
[1] WEN F, ZHANG G, SUN L, et al. A hybrid temporal association rules mining method for traffic congestion prediction[J]. Computers & Industrial Engineering, 2019, 130: 779-787.
[2] 罗向龙,焦琴琴,牛力瑶,等. 基于深度学习的短时交通流预测[J]. 计算机应用研究,2017,34(1):91-93,97.
[3] 田瑞杰,张维石,翟华伟. 基于时间序列与BP-ANN的短时交通流速度预测模型研究[J]. 计算机应用研究, 2019, 36(11):3262-3265,3329.
[4] 康军,段宗涛,唐蕾,等. 一种LS-SVM在线式短时交通流预测方法[J]. 计算机应用研究, 2018, 35(10):2965-2968.
[5] 陈雨嘉,王竞慧,韩越,等. 民航飞行员安全绩效的建模与预测——多元线性回归模型与Elman神经网络模型的比较与应用[J]. 人类工效学, 2019, 25(6):56-62.
[6] 田英杰,苏运,郭乃网,等. 基于时间序列嵌入的电力负荷预测方法[J]. 计算机应用与软件, 2018, 35(11):55-60,73.
[7] 史云扬,李牧,付野,等. 基于灰色-BP神经网络模型的多情景交通用地需求预测——以长江中游城市群为例[J]. 中国农业大学学报, 2020, 25(6):142-153.
[8] 徐东星,尹勇,张秀凤,等. 基于改进三参数灰色模型的海上交通事故预测[J]. 中国航海, 2020, 43(1):12-17.
[9] 曹洁,沈钧珥,张红,等. 基于小波和多维重构的BP神经网络交通流短时预测[J]. 计算机应用与软件,2018,35(12):61-65,82.
[10] 黄晓慧,张翠芳. 布谷鸟算法优化小波神经网络的短时交通流预测[J]. 计算机应用与软件,2017,34(3):238-242.
[11] 曹堉,王成,王鑫,等. 基于时空节点选择和深度学习的城市道路短时交通流预测[J/OL]. 计算机应用:1-10.[2020-05-31]. http://kns.cnki.net/kcms/detail/51.1307.TP.20191209.1313.008.html.
[12] 顾兆军,李冰,刘涛. 基于PSO-Elman模型的网络流量预测[J]. 现代电子技术, 2019, 42(1):82-86.
[13] 邝先验,周扬栋,宋二猛. 基于自适应GA-Elman神经网络的短时交通预测[J]. 计算机仿真,2018,35(7):103-107.
[14] ELMAN J L. Finding structure in time[J]. Cognitive Science, 1990, 14(2):179-211.
[15] HUANG N E, SHE Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971):903-995.
[16] DéGERINE S. Sample partial autocorrelation function of a multivariate time series[J]. Journal of multivariate analysis, 1994, 50(2):294-313.
(责任编辑:黄 健)
收稿日期:2020-08-14
基金项目:云南省万人计划项目(109720190106);云南省高层次人才项目(132510978220)
作者简介:李振国(1994-),男,昆明理工大学理学院硕士研究生,研究方向为数据分类与神经网络;徐建新(1983-),男,博士,昆明理工大学冶金与能源工程学院教授,研究方向为数据挖掘理论与方法。本文通讯作者:徐建新。

