结合K-SVD算法的金字塔变换域中的图像融合方法研究

许亚男 钱叶旺 王鞠庭

摘要：传统的金字塔融合方法是对金字塔分解后得到的顶层系数进行直接平均融合，其它各层系数选择绝对值大者进行融合，视觉效果上存在模糊、细节缺失等缺点。为了弥补传统金字塔融合方法的不足，对金字塔分解后的顶层采用K-SVD（K Singwar Value Decomposition）算法实现对系数的有效稀疏表达，其余层根据局部区域像素和的绝对值大小来选取系数。实验表明：采用金字塔变换方法，结合K-SVD稀疏表示的融合规则，获得的融合图像视觉上更加清晰，定量评价指标也更优;并且形态学的金字塔在相同融合规则下获得的视觉效果更好，评价指标也优于其他几种方法。

关键词：金字塔变换;融合规则;K-SVD;稀疏表示

中图分类号：TN911 文献标志码：A 文章编号：1008-4657（2020）05-0068-05

0 引言

从最初的信件、电报、电话到现在的视频交流，数字图像已经成为人们获取信息的主要来源，同时也是人们进行沟通与交流的主要媒介。图像传感器是获取数字图像信息的重要途径与手段，可以采集到不同来源的数字图像，人们可以根据采集到的图像，利用某些数学方法将这些图像进行处理得到一幅信息丰富的高质量图像，这就是图像融合。它的应用领域包括：现代化工业生产监控、基础学科研究、宇宙开发、航海探测、军事国防、医学诊断、环境保护、资源调查等[1-4]。红外图像与可见光图像融合是图像融合中的重要分支之一，红外图像是根据不同物质热辐射的不同来区分目标与背景，它不受光照的影响，能够较好的反映温度的分布，但是其空间分辨率不高，细节信息少;可见光图像是依据人的视觉系统获得物质的结构特点，具有较高的空间分辨率与对比度，细节表现能力强，但是会受到天气情况与光照的影响。根据以上两种图像的互补性，将二者融合可以发挥二者的优势，在很多领域如军事、国防、遥感、目标识别等很多领域都有应用[5-9]。

在金字塔融合方法中，对源图像进行金字塔分解得到不同层的系数，对各层系数采用加权平均、绝对值取大、系数取大等融合规则进行融合处理，获得的融合图像不够清晰，细节表现能力不强。为了得到更高质量的融合图像，本文结合K-SVD算法[10]与区域绝对值取大方法，对金字塔分解后的各层系数进行有效融合。

1 金字塔变换

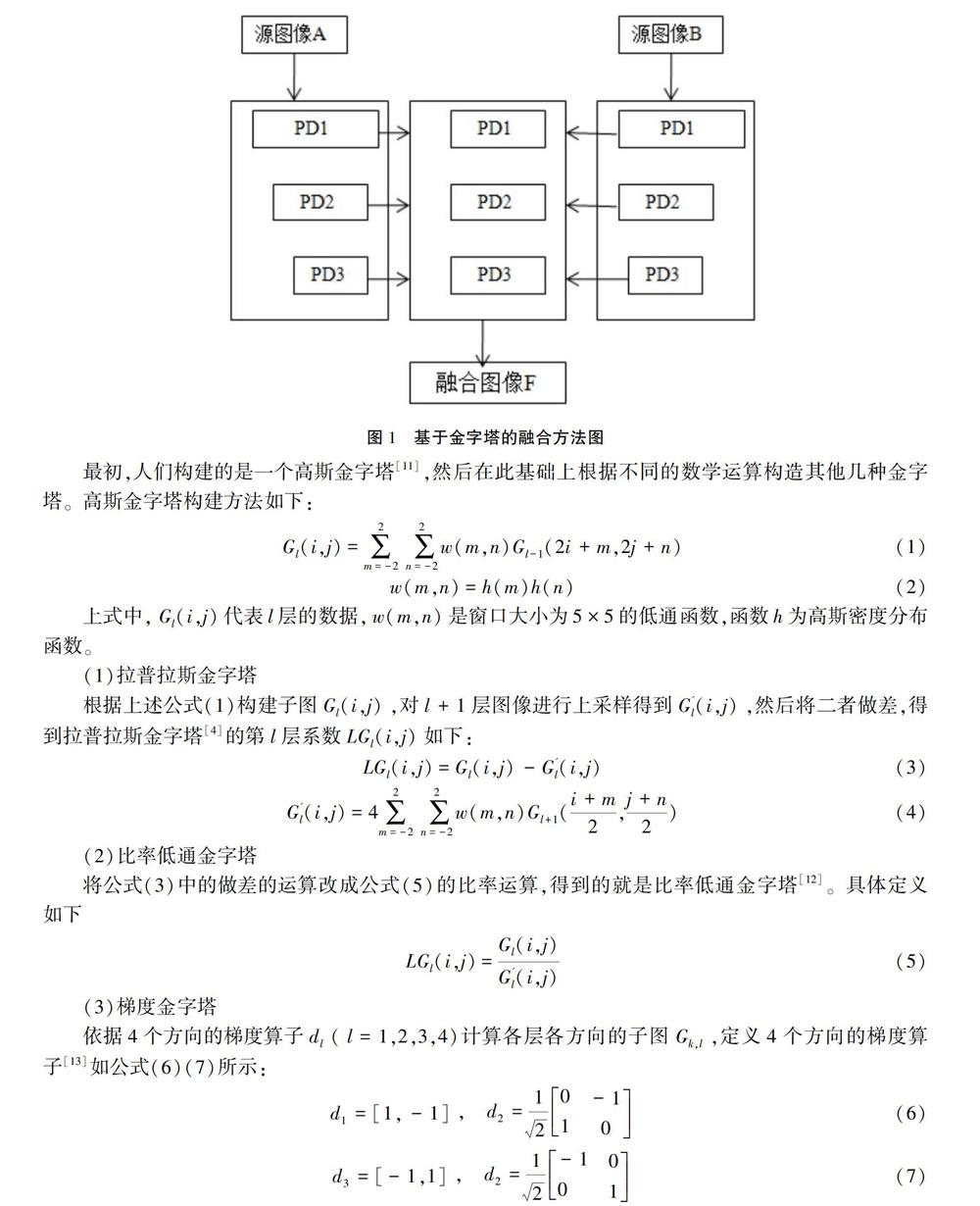
Burt P J等[11]于1983年提出了图像金字塔结构来描述图像。金字塔分解就是运用不同的算法将图像逐层分解为尺寸递减的多个图像，结构上形似金字塔。它具有多尺度特性，图像一层一层滤波后形成多个子图，这些图形按照由顶层往下构成一个金字塔的形状，是一种有效的变换域融合方法。两幅图像的金字塔融合过程如图1所示，图中A、B代表源图像，PD1、PD2与PD3代表不同分解层上的数据。然后选用不同的方法对分解所得的相同层的数据进行融合处理，获取各层新的数据，最后根据新的数据逐层进行金字塔重构，得到最终融合后的图像。

最初，人们构建的是一个高斯金字塔[11]，然后在此基础上根据不同的数学运算构造其他几种金字塔。高斯金字塔构建方法如下：

2 图像融合规则

2.1 传统的图像融合规则

总体来说融合方法主要有针对像素和区域的两种。

（1）像素加权平均

假设A（i，j）、B（i，j）分别代表两幅源图像在（i，j）处的像素值，该处融合后的像素值用F（i，j）表示，则其中，α1+α2=1，α1和α2的值可以根据实际情况来适当调整。当α1=α2=0.5时就是直接平均。

（2）像素取大

（3）区域绝对值取大

根据图像的特点将其划分成一定大小的区域，一般选择3×3 ， 5×5 ，7×7等大小的窗口。区域绝对值取大就是选择窗口内的像素和大的数据作为最终的数据。

2.2 基于K-SVD算法的稀疏表示

稀疏表示[5]就是根据给定的学习字典将信号用尽可能少的元素表示，实现用少量的信息表示信号的特征，以便达到对信号最优的表示。利用稀疏表示的思想实现对信号f（n）的最优表示，用公式表示如下上式中，f（n）表示的是稀疏函数，gi（n）表示的是信号矢量，将原信号按照gi（n）组成的集合展开，这个集合称为字典D，具体表示为D={gi}，i=1，2，...，N，字典中元素称为原子，展开的系数用ci表示，求解稀疏系数ci采用效率高的正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法[15]。由字典D选择稀疏表示[5]的模型如下其中‖x‖0代表非零项的个数，ε代表允许的误差。

K-SVD算法[16]是以训练样本为对象，从待处理的图像数据中学习得到字典，不仅可以有效的体现图像的特征，而且还可以提高字典的表达能力。构造训练字典D具体分为稀疏表示与字典更新两步：首先设定一个初始化的字典，然后用该字典对数据进行稀疏表示，得到稀疏矩阵X;接着对初始字典进行更新，使得稀疏矩阵表示的数据与原始数据之间的误差尽可能小，这样就可以得到一个可用字典，误差矩阵的数学模型表示如下其中，Y代表样本总体的集合，x代表稀疏矩阵，T0反映了稀疏的程度。

以更新字典的k列为例：设dk为字典的k列，xkT为稀疏矩阵的k行，计算误差矩阵Ek的公式如下

结合K-SVD算法的金字塔融合方法具体步骤如下：首先对源图像A、B分别进行金字塔分解，然后对分解后得到的各顶层系数采用8×8的窗口进行分块，将每个图像块编纂得到相应的列向量V1、V2，将二者组成联合矩阵V12作为初始字典;接着从图像数据V12中学习更新字典，不断迭代更新直到重建误差为0.1获得最终的冗余字典D，接着根据OMP算法选取稀疏系数x1和x2实现对图像的稀疏处理;其余各層采用绝对值取大的方法进行融合;最后将各层数据进行金字塔重构得到融合后的图像。

3 实验结果与评价

选用配准后的可见光图像与红外图像进行融合仿真实验，两幅大小为256×256的红外与可见光的灰度图像如图2所示。传统的几种金字塔融合效果对比如图3所示，分别将几种金字塔变换方法结合顶层直接平均，其余层选取像素值绝对值大的系数保留，分解层数均选择4层，然后顶层系数采用公式（11）计算融合后的系数（参数α1=α2=0.5），剩下各层系数使用公式（13）的方法计算融合后的系数。图4显示的是所有的顶层系数依据K-SVD稀疏表示（Sparse Representation，SR）算法，剩下各层依据区域绝对值取大的方法，对比几种金字塔融合的效果分别如图4的（a）、（b）、（c）、（d）所示。由图3与图4可以看出，在相同融合规则下，梯度金字塔融合的图像视觉效果最差，形态学金字塔融合后获得的图像视觉效果最好，拉普拉斯金字塔与比率低通金字塔融合后视觉效果居中。

（a）红外图像（b） 可见光图像

（a）拉普拉斯金字塔融合 （b）比率低通金字塔融合 （c）梯度金字塔融合（d）形態学金字塔融合

（a）拉普拉斯金字塔+SR（b）比率低通金字塔+SR（c）梯度金字塔+SR（d）形态学金字塔+SR

融合效果方面，视觉上取决于人的主观视觉体验，比较难掌控，也很难统一;评价指标可以比较直观的反映融合的效果。本文选用了平均梯度、边缘强度、标准差、空间频率等评价指标[17]，以上所有指标数值越大，表明融合后图像的质量越好。图3与图4对应的所有的评价指标如表1与表2所示。从表1与表2中可以看出，结合K-SVD稀疏表示算法融合后的各项指标均比加权平均得到的数值高;另外，同一种融合规则下，形态学金字塔的融合视觉效果最好，并且评价指标也最高。

4 总结

本文将几种金字塔变换结合加权平均、绝对值取大以及K-SVD稀疏表示等融合规则对图像进行融合处理，同时计算多个评价指标。分别从仿真的视觉效果与计算的评价参数上作对比，实验表明：同一种金字塔变换，分解后的顶层系数使用K-SVD稀疏表示的融合算法比加权平均算法取得了更好的效果;此外，在相同融合规则下，形态学金字塔可以获得更好视觉效果与评价指标。

参考文献：

[1] 杜进楷，丁冬冬，龙海莲，等.基于NSST和稀疏表示相结合的图像融合算法[J].电脑知识与技术，2019，15（15）：217-221.

[2] 彭延军，王瑾瑾，王元红.基于拉普拉斯金字塔改进的图像融合方法[J].软件导刊，2016，15（1）：167-170.

[3] 余美晨，孙玉秋，王超.基于拉普拉斯金字塔的图像融合算法研究[J].长江大学学报（自科版），2016，13（34）：21-26，4.

[4] 黄福升，蔺素珍.基于拉普拉斯金字塔变换方法的多波段图像融合规则比较[J].红外技术，2019，41（1）：64-71.

[5] 傅志中，王雪，李晓峰，等.基于视觉显著性和NSCT的红外与可见光图像融合[J].电子科技大学学报，2017，46（2）：357-362.