基于GIOWA算子的中国国内旅游人数预测

张婉玉

摘要：采用指数平滑法、抛物线模型和多元回归模型三种单项预测模型对1994～2018年我国国内旅游人数数据进行拟合预测，然后利用广义诱导有序加权平均算子将三种单项预测模型进行组合，分别探讨了λ=1，λ=0，λ=-1，λ=1/2时的组合预测结果，结果显示，组合预测的精度和效度完全高于各个单项预测结果;利用组合预测模型对未来3年我国国内旅游人数进行预测，未来三年我国国内旅游人数将会以6%左右的涨幅增加。

关键词：GIOWA算子;旅游人数;组合预测

中图分类号：F592.7 文献标志码：A 文章编号：1008-4657（2020）05-0021-08

0 引言

旅游业是第三产业的重要组成部分，改革开放以来，我国的旅游市场规模稳步扩大，发展前景十分可观，既能带动经济发展，扩大就业，还可以提升当地基础设施的建设和公共交通的建设。然而，由于2020年初的新冠肺炎疫情，各地采取严格的隔离措施，封锁海关、取消航班，对各国各地的旅游业产生了严重影响。合理估计疫情引起的损失，规划和发展国内旅游业，需要更精准的预计未来的旅游人数。

1969年，Bates J M等[1]对组合预测方法进行了比较系统的研究，引起了广泛关注。随后国内外学者在最优组合预测方法的基本理论、组合预测权重的计算、以及非负权重预测方法等方面展开了大量研究[2-5]。在利用组合预测方法进行预测方面，我国学者的研究也有很多，熊巍等[6]选择指数平滑法、季节性差分自回归滑动平均模型（Seasonal Autoregressive Integrated Moving Average，SARIMA）、反向传播（Back Propagation，BP）神经网络模型和灰色系统模型，利用误差平方和倒数最小的准则确定权重构建组合预测模型，对农产品的市场价格进行了预测。刘智禄等[7]通过灰色系统模型（Grey Model，GM）和BP神经网络的组合模型预测西安市2018～2020年的房价。梁晓莹[8]基于自回归差分移动平均模型（Autoregressive Integrated Moving Average，ARIMA）和支持向量机模型（Support Vector Machines，SVM）对郑州市CPI进行预测，实证结果显示组合预测的预测结果更准确。

我国关于旅游需求的预测大多采用单项预测模型。李军言等[9]利用ARIMA模型对我国入境旅游人数进行预测分析，发现因世界经济低迷的影响，目前我国入境旅游处于收缩阶段。王敬昌等[10]采取分时序分段策略，利用卷积神经网络提取景区多因素时序数据特征，结合预测时刻的情境信息预测短期景区内游客人数。陈鹏等[11]通过ARIMA模型对安徽省1995～2010年的入境旅游人数进行预测。王曉霞等[12]利用灰色预测模型，得到了牡丹江市的旅游人数的规律。现有研究在利用组合预测对旅游人数进行预测时，主要选择某一种最优性准则，例如，吴良平等[13]选择短记忆预测模型和长记忆预测模型对中国入境旅游人数进行了预测，然后将各单项预测模型利用诱导有序加权调和平均算子（Induced Ordered Weighted Harmonic Averaging Operator，IOWHA）进行组合，有效提高了预测精度。刘盛宇等[14]利用误差平方和最小的准则，选取Holt-Winters非季节指数平滑模型，自回归分布滞后模型，以及局部多项式回归模型对1978～2011年的国际旅游外汇收入进行预测。王洋[15]利用IOWA算子将灰色系统模型，指数平滑模型，和BP神经网络模型的预测结果组合起来，更精确地预测了成都的入境旅游需求。广义诱导有序加权平均（Generalized Induced Ordered Weighted Averaging，GIOWA）组合预测模型是更广泛意义的组合预测模型，在λ为不同值时，分别对应不同的最优性准则。本文采用指数平滑模型、抛物线模型和多元回归模型，利用GIOWA算子对国内旅游人数进行组合预测，以求更加精确的预测未来旅游人数变化。

1 单项预测方法的拟合预测

1.1 指数平滑法

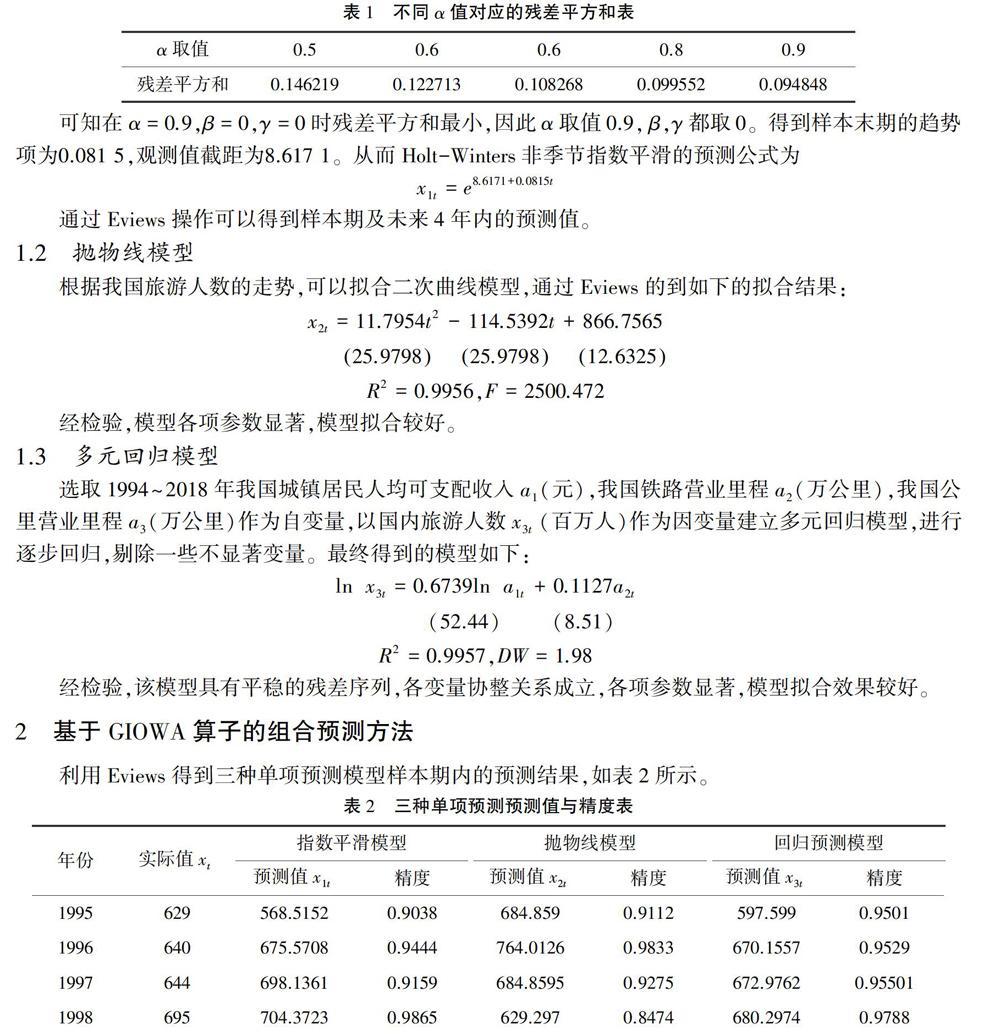
对我国1994～2018年国内旅游旅游人数进行分析，可以发现，数据呈明显的上升趋势，因此可以选择较大的α值。通过Eviews对不同α对应的残差平方和进行比较，结果如表1所示。

1.3 多元回归模型

选取1994～2018年我国城镇居民人均可支配收入a1（元），我国铁路营业里程a2（万公里），我国公里营业里程a3（万公里）作为自变量，以国内旅游人数x3t（百万人）作为因变量建立多元回归模型，进行逐步回归，剔除一些不显著变量。最终得到的模型如下：

2 基于GIOWA算子的组合预测方法

4 预测结果分析

由于GIOWA组合预测模型在样本期内具有较高的预测精度，下面分别对于λ取不同值用GIOWA组合预测模型预测2019～2022年我国国内旅游人数。

由于变权重GIOWA组合预测模型在样本期内是根据预测精度作为诱导值，在每一时点对每一种单项预测方法按照预测精度由大到小进行赋权w1w2w30。然而在预测期，由于没有实际值作比较，无法计算预测期每一个时点各种单项预测方法的预测精度，也就无法确定各种单项预测方法的预测权重。对此，本文用简单平均法得到三种单项预测方法在预测期的权重分别为：在λ=1时的权重向量为（0.134 7，0.458 3，0.407 0）T;在λ→0时的权重向量为（0.17，0.445 3，0.354 2）T;在λ=-1时的权重向量为（0.213 7，0.430 4，0.355 9）T;在λ=12时的权重向量为（0.142 1，0.458 3，0.383 0）T。