基于模板聚类的在线签名认证方法
汤升庆 胡华成


摘要:提出基于模板聚类的两级签名认证方法。首先将注册的签名进行比对获得相似度得分矩阵,取所有相似度得分的中位数作为一个聚类阈值。然后利用签名阈值聚类算法将注册签名进行聚类,在每个签名聚类中选择与其它签名相比总得分最高的签名作为该签名聚类的签名代表,作为一级模板签名;各个签名聚类中的其它签名作为二级模板签名。最后通过相似度评判依据,在两个公开数据集SVC2004 Task 1、SUSIG Visual上选择不同数量的真实样本进行模板聚类,剩余真实样本和熟练伪造样本作为测试样本进行了实验对比。根据不同训练签名样本数,在两个数据集上的等错误率(Equal Error Rate,EER )分别是2.50%和0.83%,验证了本文方法的有效性。
关键词:模板聚类;阈值聚类;曲线相似;融合特征
中图分类号:TP391.41 文献标志码:A 文章编号:1008-4657(2020)05-0060-08
0 引言
使用手写签名进行个人身认证或验证是广泛研究的行为生物识别技术之一,也是身份验证最流行的方法之一[1]。手写签名代表了一个人进行书写的行为特征,通常,签名验证系统可以分为两类,即离线系统和在线系统,两者有显著的区别。离线签名历史悠久,而在线签名更难模仿与伪造。这是由于在线签名的特征信号能够保持书写的位置轨迹、压力、高度和方位角等动态时间序列特征,具有更强的鲁棒性和更高的安全性。
虽然签名可以显示个人行为特征,但它与指纹识别、虹膜识别和人脸识别等其他固有生物特征识别技术相比差异较大。手写签名具有可变性,书写者自身及环境的影响因素更多,简单来说,对于同一个书写者的两次签名重复永远不会完全相同[2]。
当前的手写签名认证主要有两种不同类型的方法,一是基于统计参数的方法,通过统计大量同一人的签名提取有区分度的统计特征来鉴别签名真伪,包括统计分类[3-4]、神经网络[5]、支持向量机(Support Vector Machine,SVM)[6]等。另外一种是基于函数的方法,将动态签名的信号数据看作时间的函数,并通过将参考签名与测试签名直接进行比较来验证签名者。一类函数方法是将注册签名作为模板,通过模板匹配的方式来进行匹配,比如有动态时间弯曲(Dynamic Time Warping,DTW)[7-8]和隐马尔可夫模型(Hidden Markov Model,HMM)[9-10]。另外,基于函数变换或重构后,提取有区分度的判别特征也是非常有效的方法,比如快速傅里叶变换(Fast Fourier Transform,FFT)[11]、小波包[12]、混合高斯模型(Gaussian Mixture Model,GMM)[13]和离散余弦变换(Discrete Cosine Transform,DCT)[14]。
基于函数的认证系统利用了与签名相关的所有原始信息,对比基于统计参数的系统表现出更好的性能。目前,为提高验证精度而进行的融合已成为一种有前途的趋势,文献中经常采用参数方法和函数方法相结合的方法[14-17]。
通常,签名之间需要匹配过程或特殊的函数参数计算,需要花费更多的时间和更多的空间。文献[18]提出了一种基于曲线相似的签名认证方法,当注册签名模板数目多的时候,计算量大。此外,仅仅依赖曲线间的相似距离,签名认证系统的性能有限。有鉴于此,本文提出基于模板聚类两级签名认证方法。首先,将注册的签名进行一一比对获得相似度得分,以相似度得分矩阵为基础,采用基于阈值的顺序聚类方法将注册签名进行聚类,每个签名聚类中选择与其它签名相比总得分最高的签名作为该签名聚类的签名代表,并作为一级模板签名;各个签名聚类中的其它签名作为二级模板签名。通过聚类,将从大量注册签名寻找具有代表性的签名模板。在每个签名一一比对过程中,本文提出了一种融合曲线相似距离和时间速度比加权的特征作为签名相似度评判依据,改进了文献[18]提出的曲线相似距离作为特征计算的签名认证方法。实验结果验证本文方法的有效性。
1 签名相似度计算
将签名的X、Y坐标看作平面曲线,可以使用曲线相似方法来计算曲线间的相似距离。图1 为2个签名数据及签名X、Y曲线。
我们在二维平面曲线进行直接匹配,改进文献[18]中的分段曲线匹配算法。将参考曲线划分为K段,每条分段参考曲线有m个数据点。比较曲线与各参考分段曲线的优化匹配计算如下。
1.1 参考曲线分段划分
首先,对于參考曲线,每个分段曲线可定义为:
1.2 参考曲线分段划分
同样,对于比较曲线,对应于参考分段曲线,比较分段曲线的每个可能的匹配间隔可定义为
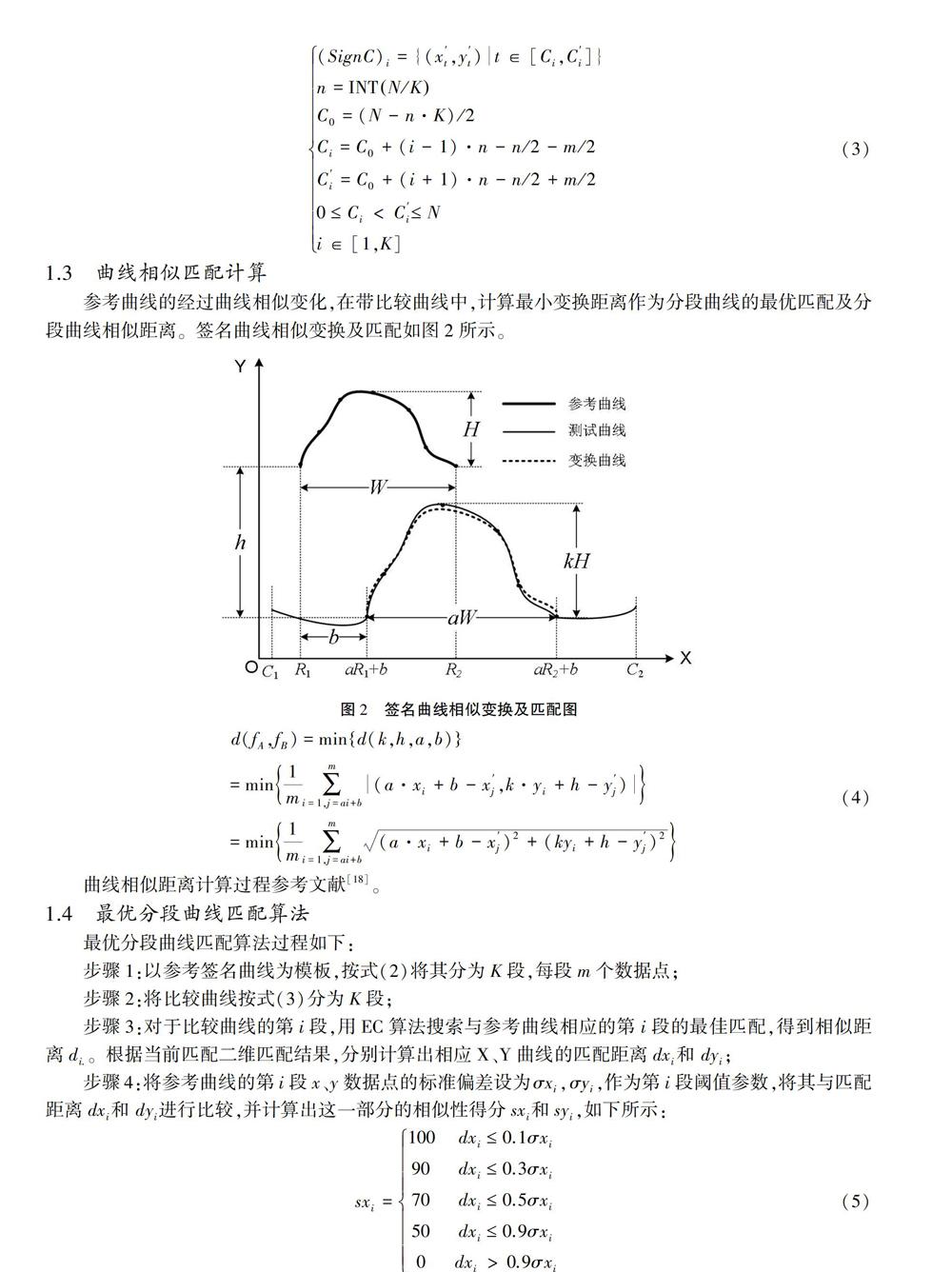
1.3 曲线相似匹配计算
参考曲线的经过曲线相似变化,在带比较曲线中,计算最小变换距离作为分段曲线的最优匹配及分段曲线相似距离。签名曲线相似变换及匹配如图2所示。
1.4 最优分段曲线匹配算法
最优分段曲线匹配算法过程如下:
步骤1:以参考签名曲线为模板,按式(2)将其分为K段,每段m个数据点;
步骤2:将比较曲线按式(3)分为K段;
步骤3:对于比较曲线的第i段,用EC算法搜索与参考曲线相应的第i段的最佳匹配,得到相似距离di.。根据当前匹配二维匹配结果,分别计算出相应X、Y曲线的匹配距离dxi和 dyi;
步骤4:将参考曲线的第i段x、y数据点的标准偏差设为σxi,σyi,作为第i段阈值参数,将其与匹配距离dxi 和 dyi进行比较,并计算出这一部分的相似性得分sxi 和syi,如下所示:
1.5 区间速度比计算
在第i个分段曲线匹配区间[Ri,Ri+1]中,对应点的区间速度比(IVR)计算如下:
1.6 签名曲线的相似度得分计算
两条签名曲线的相似性度得分Score由局部得分LSC和和全局得分GSC加权而成,计算如下:
2 签名模板聚类及认证算法
2.1 签名阈值聚类
假设某个签名注册模板集合为P={F1,F2,…,Fp}。对集合P中每个签名进行一一比对,则签名相似度得分矩阵如下:
2.2 两级签名认证
按照上述签名聚类算法过程,签名模板P={F1,F2,…,Fp}将聚成Q={Q1,Q2,…,QT}共T个类别。在每个签名聚类中Qi中,将与该签名聚类其余签名相似度得分最高的签名作为一级模板,并标记Qi0。 则一级模板签名集合为Q={Q10,Q20,…,QT0}。
給定待测签名F,两级签名认证算法如下:
步骤 1:将待测签名F与一级签名模板Q一一比对,计算相似度得分,取相似度得分最高的签名所代表的签名聚类QT,如果最高得分小于一级签名模板得分,则该签名直接判断为伪造签名;
步骤2:在签名聚类QT中,如果QT中签名模板个数大于2,则随机选择两个签名作为2级模板,计算待测签名与两个签名一一比对的相似度得分,取平均值作为2次综合得分,如果该得分大于判别阈值,则该签名为真实签名;否则为伪造签名;
步骤3:如果QT中签名模板个数小于1,则在一级模板中选择2个最好得分的均值作为2次判别的综合得分,同样,如果该得分大于判别阈值则该签名为真实签名;否则为伪造签名。
3 实验及结论
本文采用两个签名数据集对算法进行评估。一是SVC2004 Task1(SVC1)(1)数据集,含40位签名者,每位20个真实签名和20个熟练伪造签名。二是SUSIG Visual(SUSIG)(2)数据集,含94位签名者,每位有20个真实签名和10个熟练伪造签名。两个数据集中,每位签名者的20个真实签名均分为2个阶段书写。因此,本文的验证方法是分别选择前5、10、12个真实签名进行签名模板聚类,剩余的真实签名和熟练伪造签名作为测试签名。
计算真实样本、伪造样本的比对结果,以误拒率(False Rejection Rate,FRR)、误纳率(False Acceptance Rate,FAR)计算的等误率(Equal Error Rate,EER)进行结果统计。结果如图5~6所示,其中TS用于模板聚类的注册签名数。
从表2可以看到,本文提出的方法在SUSIG数据库上获得最优结果。在SVC1数据集上,从表1可以看到,当训练样本数为12时,本文方法取得最好结果;而当训练样本数为5时,与其它优秀算法性能相当。由于SVC1数据集中真实签名分两阶段时间采集(间隔一周),前后差异较大,当训练签名包含第二阶段样本时,模型认证结果迅速降低,说明增加第二阶段注册签名后提取的一级模板更加多样化和具备代表性。同时,与文献[18]的曲线相似方法相比,我们改进了分段匹配算法并提出了新的融合特征,其EER得到极大提高,使用5个模板训练时,在SVC1上EER从10.92%降低到6.58%,相应的在SUSIG上EER从2.89%降低到1.26%。
注释:
(1) SVC2004 Task1 数据集https://www.cse.ust.hk/svc2004/results-EER1.html.
(2) SUSIG Visual(SUSIG)数据集http://biometrics.sabanciuniv.edu/susig.html.
参考文献:
[1] Hammoud R I,Abidi B R,Abidi M A.Biometrics: Personal Identification in Networked Society[M].Biometrics: Personal Identification in Networked Society.New York: Springer-Verlag,2005.
[2] Diaz M,Fischer A,Ferrer M A,et al.Dynamic Signature Verification System Based on One Real Signature.[J].IEEE Transactions on Cybernetics,2018,48(1): 228-239.
[3] 刘莉,詹恩奇,郑建彬,等.基于曲线分段相似匹配的在线签名认证[J].计算机应用,2018,38(4):1 046-1 050,1 133.
[4] Ibrahim,Kyan,Guan L.On-lineSignature Verification Using Global Features[C].Conference on Electrical & Computer Engineering.NL: IEEE,2009.
[5] Tang L,Kang W,Fang Y.Information Divergence-Based Matching Strategy for Online Signature Verification[J].IEEE Transactions on Information Forensics & Security,2018,13(4):861-873.
[6] Gruber C,Gruber T,Krinninger S,et al.Online Signature Verification With Support Vector Machines Based on LCSS Kernel Functions[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B (Cybernetics),2010,40(4):1 088-1 100.
[7] 张梓轩,贺也平.基于信号序列的在线签名认证方法及应用[J].计算机工程与设计,2018,39(3):824-830,901.
[8] Abhishek Sharma,Suresh Sundaram.A Novel Online Signature Verification System Based on Gmm Features in a Dtw Framework[J].IEEE Trans.Information Forensics and Security,2017,12(3): 705-718.
[9] Wada N,Hangai S.HMM Based Signature Identification System Robust to Changes of Signatures with Time[C].IEEE Workshop on Automatic Identification Advanced Technologies.Alghero:IEEE,2007.
[10] Shafiei M M,Rabiee H R.A New On-Line Signature Verification Algorithm Using Variable Length Segmentation and Hidden Markov Models[C].International Conference on Document Analysis & Recognition.Edinburgh: IEEE Computer Society,2003.
[11] Berrin Yanikoglu,Alisher Kholmatov.Online Signature Verification Using Fourier Descriptors[J].EURASIP Journal on Advances in Signal Processing,2009(1): 1-13.
[12] Wang K,Wang Y,Zhang Z.On-line Signature Verification Using Wavelet Packet[C].International Joint Conference on Biometrics.DC: IEEE,2011.
[13] Xia Xinghua,Chen Zhili,Luan Fangjun,et al.Signature Alignment Based on Gmm for On-line Signature Verification[J].Pattern Recognition,2017,65: 188-196.
[14] Rashidi S,Fallah A,Towhidkhah F.Feature Extraction Based Dct on Dynamic Signature Verification[J].Scientia Iranica,2012,19(6): 1 810-1 819.
[15] Barkoula K,Economou G,Fotopoulos S.Online Signature Verification Based on Signatures Turning Angle Representation Using Longest Common Subsequence Matching[J].International Journal on Document Analysis and Recognition ,2013,16(3): 261-272.
[16] Marcos Faundez-Zanuy.On-line Signature Recognition Based on Vq-dtw[J].Pattern Recognition,2006,40(3): 981-992.
[17] Fierrez-Aguilar J,Nanni L,Jaime Lopez-Pealba,et al.An On-Line Signature Verification System Based on Fusion of Local and Global Information[C].International Conference,Avbpa,Hilton Rye Town.NY:Springer Berlin Heidelberg,2005.
[18] 邱益鳴,胡华成,郑建彬,等.基于曲线相似的在线签名认证方法[J].系统工程与电子技术,2014,36(5):1 016-1 020.
[责任编辑:郑笔耕]

