大港口和省会城市经济辐射范围比较

吴潇林

摘要：以“中心-外围”模型为理论基础，利用1998～2016年县域经济面板数据，研究在泛珠三角地区，到以香港为代表的大港口和省会城市的距离与当地县域经济增长的关系，并进一步测算和对比大港口与省会城市辐射范围及变动趋势。研究发现：到大港口的距离和当地县域经济增长为“U”型关系;到省会城市的距离与当地县域经济增长为准“∽”型关系。以“U”曲线的极值点为大港口的辐射半径，“∽”曲线的拐点为省会城市的辐射半径。研究发现，受国内、外政治经济环境变动的影响，大港口的经济辐射范围随着时间变化不断减小，而省会城市的经济辐射范围在总体上不断增加。因此对于沿海县域而言加强与省会城市的联系将更有利于当地经济发展。

关键词：大港口;省会城市;经济辐射范围

中图分类号：F061.5 文献标志码：A 文章编号：1008-4657（2020）05-0040-11

0 引言

改革开放四十年，中国的经济生产资料向东部沿海集中，出口带动经济增长，此时大港口承担着带动周围经济增长的增长极作用。之后国家出台地区性平衡发展战略，资源向中西部地区倾斜，大港口的中心地位受到一定程度动摇。最后由于国际金融危机的影响，外向型经济难以继续承担作为中国经济发展引擎的作用，国家着力扩大内需，大港口的地位继续下滑[1]。与此同时，省会城市的建设得到重视，部分省份不断强化提升省内中心城市首位度的政策导向，增强省会的增长极作用以拉动省内经济的发展[2]。

然而，无论是作为地区增长极的大港口或是省会城市，目前学术界对于两者经济辐射范围的测度较少，经济辐射范围的对比更是不足。因此本文以“中心-外围”理论为基础，利用泛珠三角地区9省，1998～2016年县域经济面板数据，研究以香港作为代表的大港口和省会城市对周边经济辐射范围的变化。并基于研究结果，尝试对沿海地区县域经济的发展给出一点建议。

1 文献综述

经济辐射是指中心地区作为经济发展水平和现代化程度较高的地区，通过知识外溢、技术扩散、生产联动等的方式，提高落后地区的资源配置效率，从而达到拉动落后地区社会经济发展的现象[3]。

在衡量经济辐射范围方面，现有文献大致有三种方法：

首先是经验判断。荣兆梓等[4]认为长三角的辐射范围大致是以上海为圆心，600公里为半径的圆所覆盖的地域。这种方法缺乏数据支撑，主观性太强。

第二种方法是将空间引力模型和断裂点法结合，通过计算中心城市与周边城市的经济联系量来测度中心城市的辐射范围。在测算粤港澳大湾区的经济辐射范围时，陈子真等[5]通过该方法得出在大湾区内，作为核心的三大城市中，香港的经济辐射范围大于广州，深圳最小。然而这种方法的不足之处在于，是用中心城市一对一地计算与周围城市的联系，并且更加注重的是辐射强度，缺乏从总体上对中心城市辐射范围的计算。

第三种方法是以新经济地理学的“中心-外围”理论为基础，利用计量方法计算中心地区的辐射范围。其理论基础是克鲁格曼的“中心-外围”模型。该模型强调区域存在使要素往中心地区聚集的向心力以及使要素远离中心地区的离心力[6]。将向心力和离心力应用于城市发展体系中，Fujita M等[7]发现，在单一的城市体系中，当地经济的发展与到中心地区的距离有类似于“∽”型的三次方关系。即随着距离的增加，当地经济的发展水平逐步下降，此时向心力发挥主要作用;当超过了某一临界值，离心力占据主导，此时距离中心越远经济发展越好;之后距离进一步增加又会导致经济发展水平下降。基于此，许政等[8]运用我国城市面板数据模型以人均GDP的增长率衡量当地经济增长情况，证明了到大港口的距离和当地经济增长存在这种关系。孟可强等[9]进一步将“∽型”曲线的第一个极值点作为中心地区的辐射范围，得出了中国三大都市圈中心城市各自的辐射范围。由此可以看出这种方法对中心地区的辐射范围有比较清晰的把握，因此本文采用第三种方法测算中心地区的经济辐射能力。

但是现有文献在运用该方法对中心地区测算经济辐射范围时还存在不足。首先港口和省会城市相对于其它地区都有资金、技术、人力资源、政策等方面的优势，因此都会成为该地区的中心增长极[10]。但是当前文献缺少对两者辐射范围的横向对比，在一个既靠近港口又靠近省会城市的地方，究竟受到何者的经济辐射影响尚不明白;其次，港口和省会城市的经济辐射范围是随着内部条件和外部环境的变化而不断变化的[11]，不同的时间截点两者的辐射范围不同，但是目前尚未有文献分时间截点讨论二者经济辐射范围变化;最后是以上研究成果大多基于城市层面上得出的结论，由于我国的地域间差异明显，不同尺度的统计数据可能得出不一样的结论，越小尺度的数据得出越加细致的结论[12]。因此在已有文献的基础上，本文运用县域经济数据来测算大港口和省会城市的经济辐射范围，并对比分析其变化。

2 数据和研究方法

2.1 研究范围

泛珠三角地区，是由东部地区的广东、福建、海南，中部地区的江西、湖南，以及西部地区的四川、云南、贵州、广西9个省区加上香港、澳门两个特别行政区组成，拥有占全国五分之一的國土面积、三分之一的人口以及三分之一以上的经济总量，是我国最具有活力和发展潜力的地区之一。2016年，深化泛珠合作正式写入“十三·五”规划，国务院正式发布了《关于深化泛珠三角区域合作的指导意见》，泛珠三角区域合作全面上升为国家战略。由此可见，选择泛珠三角地区进行研究具有重要的现实意义。泛珠三角地区的地理位置，如图1所示。

2.2 研究方法

本文的理论基础是城市体系中的“中心-外围”模型[13-14]。由于受到向心力和离心力的影响，到中心地区的距离与当地的经济发展水平之间存在着“∽型”的关系。参考许政等[8]、孟可强等[9]以及陆铭等[15]模型设计和变量选取，本文建立的基准计量模型（1）如下：

模型的被解释变量Yit为i县t年的的实际人均GDP取对数，其中数据均以1998年为基期按各省份通货膨胀指数进行消胀，用Ln人均gdp表示。解释变量disport和discity分别表示在泛珠三角地区当地县域到香港和到本省省会的直线距离;disport2、disport3和discity2 、discity3则表示对应disport 和discity变量的二次项和三次项;Xit 代表其它会影响当地经济县域经济发展的控制变量;T表示一组控制时间因素的年份虚拟变量。其他为常数。

本研究中，我们使用来自历年《中国县域统计年鉴》中1998～2016年的县域经济面板数据。因为剔除了香港、澳门两个特别行政区以及一些县域行政区发生变动的地区，所以共包含741个县域19年的经济数据。然而由于存在数据的缺失，个别变量的观察值小于14 079（741×19）个。模型的被解释变量Yit为第i县t年的的实际人均GDP取对数，数据均以1998年为基期按各省份通货膨胀指数进行消胀，用Ln人均gdp表示。

解释变量方面，本文主要关注的是在泛珠三角地区各县域到香港的直线距离和到本省省会城市的直线距离（单位：公里），分别用disport和discity表示。数据通过ArcGIS软件计算得出。

除了距离，基于以往的参考文献以及數据的可得性，本文还加入了以下会影响县域经济发展的控制变量：

固定资产投资额占当地GDP的比重，用来衡量县域经济的增长受投资的影响程度。

政府财政支出占当地GDP的比重，用来衡量地方政府对当地经济的干预程度。

第二产业产值和第三产业产值之比，用来衡量地方的产业结构。

就业，用第二产业和第第三产业业就业人数之和占总人口的比重来衡量。由于在新经济地理学中，集聚效应主要发生在非农部门，并且农业部门存在隐性失业，因此仅考虑第第二产业业和第第第三产业业业的就业人数占总人口的比重作为衡量就业的指标。

用每万人学生数作为衡量该地域经济人力资本水平。

加入是否属于河港城市地区和是否属于海港城市地区做为衡量地理因素的两个虚拟变量。因为河港以及海港等这些港口城市，在新经济地理学中存在“先发优势”和“锁定效应”、，有利于地区经济的增长。本文都把不属于港口城市作为参照组，其中河港城市与海港城市名单来源于“首届中国港口城市市长会议高峰论坛”。

加入东、中、西部虚拟变量，东部地区为参照组。

为了控制时间固定效应，加入年份虚拟变量。

变量具体的描述性统计值，如表1所示。

在回归方法的选择上，由于核心解释变量是直线距离，这一不随着时间变化的因素，因此不采用面板固定效应模型，同时为了控制异方差，本文采用面板数据FGLS模型回归。

3 实证分析

3.1 模型实证结果

为了能有更好的拟合效果，本文在运用基准模型分析到大港口和省会城市的距离对县域经济的影响，先从距离的一次项开始，逐渐往模型中增加距离的高次项。在模型（1）中先加入到大港口的距离和到当地省会城市距离的一次项，回归结果都显著。

之后依次加入距离的二次项和三次项，得模型（2）。我们发现仅有到省会城市的距离近似满足“中心-外围”理论预测的“∽”型，而到大港口的距离则与预期相反，呈现倒“∽”型。虽然在统计上，到大港口的距离和当地县域经济发展的水平是显著的，但是一方面倒“∽”型在实际上与我国外向型经济发展模式不符合，其次根据谢宇[16]的《回归分析》，“在计量经济学中只要不存在重复观察值，那么总能找到一个足够高次的多项式回归模型可以完全拟合数据，然而这样的多项式并不能正确地表达x和y之间的关系，因此有时我们需要根据非统计原因来选择模型。”

所以本文剔除到大港口距离的三次方向，得到回归模型（3），再次进行回归。此时到大港口的距离和当地经济增长之间存在显著的“U”型关系，即随着到港口距离的增加，当地县域经济的增长呈现先减少后增加的趋势。而到本省省会城市的距离和当地县域经济增长之间的关系呈现不存在极值点的准“∽”型关系。模型（1）～（3）回归结果如表2所示。

由表2结果可知，到大港口的距离和当地县域经济的增长没有出现预期的“∽”型关系。相较以往文献以城市为研究单位，县域的经济体量太小，容易受到附近发展较好的区域性中心城市影响：要么因为靠近大港口从而靠近国外市场，要么因靠近内陆中心城市而靠近国内市场;不存在因为同时远离国内市场、国外市场导致超过距离的第二个极值点后当地经济下滑。所以从整体来看县域经济到大港口的距离呈现“U”型关系。本文以二次函数的极值点作为大港口的辐射范围，根据回归结果计算得出，极值点位于距离大港口598公里处，即平均来说在泛珠三角地区香港的辐射范围，大约是以香港港口为圆心半径是598公里的圆所覆盖的地区。基于回归结果绘制到大港口与当地县域经济的关系，如图2所示。

而到本省省会城市的距离和当地县域经济增长呈现不存在极值点的准“∽”型关系。即随着到省会城市距离的增加，当地县域经济增长呈现出速度放缓地减少，超过拐点后形成速度增加地减少的关系。没有出现“中心-外围”理论预测的两个极值点的原因在于，作为省内中心地的省会城市通过向外辐射带动本省其他地方的经济增长，然而随着距离的增加，省会城市的经济辐射范围逐渐减弱。我国的省际边缘地区通常地形地貌复杂、自然灾害多，客观上会增加省会城市经济辐射的难度。因此超过拐点后对当地县域经济的辐射会加速减少。综上，选择距离的拐点做为衡量省会城市在该省份经济辐射范围的半径。通过回归模型（3）计算得出拐点为343公里。绘制到本省省会城市距离与当地县域经济增长的关系，如图3所示。

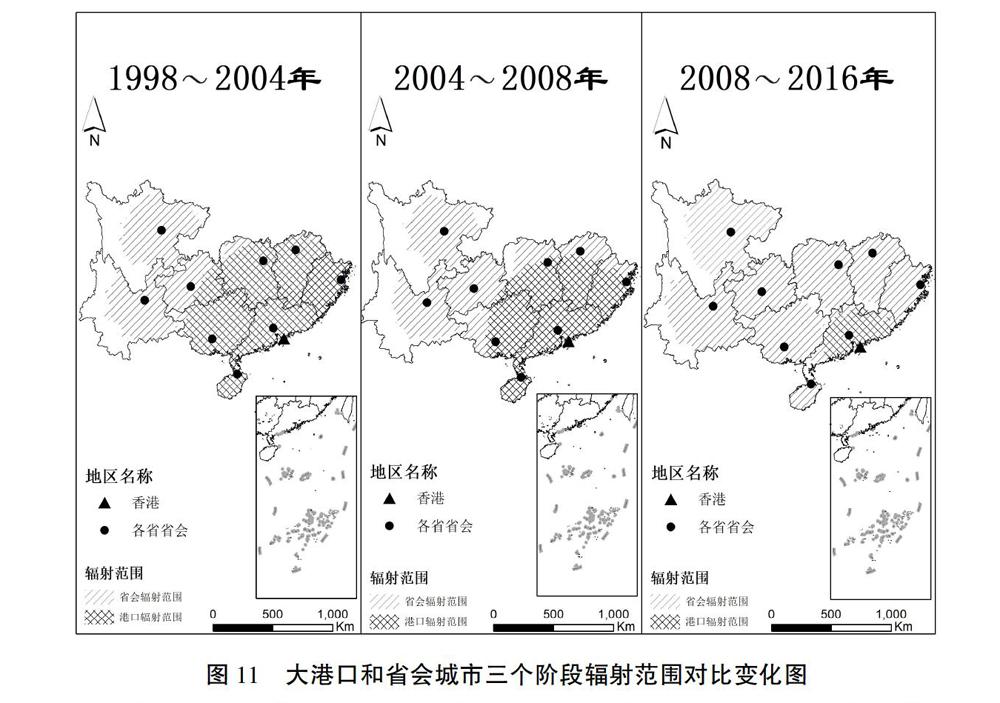
通过ArcGIS软件画出港口和省会城市的辐射范围，如图4所示。

[6] Krugman P，Elizondo P L. Trade Policy and the Third World Metropolis[J].Journal of Development Economics，1996，49（1）：137-150.

[7] Fujita M，Mori T. Structural Stability and Evolution of Urban Systems[J].Regional Science and Urban Economics，1997，27（4）：399-442.

[8] 许政，陈钊，陆铭.中国城市体系的“中心-外围模式”[J].世界经济，2010，33（7）：144-160.

[9] 孟可强，陆铭.中国的三大都市圈：辐射范围及差异[J].南方经济，2011（2）：3-15.

[10] 李红兵，佟东.论中国港口业发展现状及其在国民经济发展中的作用[J].山东社会科学，2014（1）：144-149.

[11] 任美锷，杨宝国.当前我国港口发展条件分析——兼论上海国际航运中心[J].地理学报，1998（3）：3-5.

[12] Fang Chuanlin，He Sanwei，Zhang Wenting. A Geospatial Analysis of Multi-scalar Regional Inequality in China and in Metropolitan Regions[J].Applied Geography，2017，88：199-212.

[13] Fujita M，Krugman P. When Is the Economy Monocentric？： von Thünen and Chamberlin Unified[J].Regional Science and Urban Economics，1995，25（4）：505-528.

[14] Fujita M，Mori T. The Role of Ports in the Making of Major Cities： Self-agglomeration and Hub-effect[J].Journal of Development Economics，1996，49（1）：93-120.

[15] 陸铭，向宽虎.地理与服务业——内需是否会使城市体系分散化？[J].经济学（季刊），2012，11（3）：1 079-1 096.

[16] 谢宇.回归分析[M].北京：社会科学出版，2010：193-215.

[17] 陆铭.城市、区域和国家发展——空间政治经济学的现在与未来[J].经济学（季刊），2017，16（4）：1 499-1 532.

[18] 胡求光，李洪英.金融危机对中国出口贸易影响的实证分析[J].国际贸易问题，2010（3）：3-11.

[19] 方创琳.中国城市发展方针的演变调整与城市规模新格局[J].地理研究，2014，33（4）：674-686.

[责任编辑：许立群]