数学类课程的融合教学

张东

[摘           要]  高校各数学类课程知识点之间存在紧密的联系，相互关联构成一个完整的知识体系。但在传统的教学模式中没有强调这种联系。随着慕课网络教学平台的广泛应用，教师在不断尝试创新教学方式方法，跨课程融合教学就是其中一种行之有效的教学模式。这种教学模式可以充分利用网络平台资源，将各数学课程融会贯通，帮助学生更高效、更深刻、更全面地掌握所需数学知识，构建一个立体的数学体系。

[关    键   词]  高校数学;跨课程;融合教学

[中图分类号]  G642                     [文献标志码]  A              [文章编号]  2096-0603（2020）09-0094-02

高校数学课程是针对理、工、经、管类学生开设的十分重要的公共基础课程。各大高校都应重视数学课程的教学工作，大胆地创新和尝试，以期提高数学课程的教学效率，提高学生的基础素质。而随着信息技术的发展及其在教学过程中的应用，对传统的教学模式形成不断的冲击。在慕课等教学模式被广泛推广和普及的大背景下，我们提出了“跨课程融合教学”的教学理念。

一、融合教学的提出

包含高等数学在内的这些数学类课程，也是所有课程中比较难学的课程。同时，有很多学生在完成了这些数学类课程的学习以后，仍不知道学到的这些数学知识在往后的工作学习中能起到什么作用。造成这种局面的原因很多，其中一个就是课程设置。

在传统的教学模式中，以教师的灌输式教学为主，老师会按照固定的教学方案和进度来进行教学。比如说理工科学生在大学学习过程中，至少需要学习3门以上的数学类课程。这些课程在讲授环节中都是相互独立的，且往往由不同的教师授课，每位老师负责讲好自己的课程就好，不会去花费本就紧张的课时去讲解其他课程的内容。这样就导致了各门课程之间不能很好衔接，这样更加增大了学生学习的难度[1]。学生学完后难以融会贯通，不能对数学体系形成一个整体概念。

而事实上，所有这些数学课程之间，乃至于与其他课程之间，都存在着大量的知识点关联，甚至在部分课程中，存在着相似程度极高的重复知识点。这些知识点构成了一个完整的体系。虽然我们将这个体系分解为一些独立的课程来进行学习，但不可能完全切断它们之间的联系。忽视这些联系，我们的学习过程就如同管中窥豹。所以我们需要改变这种形式，重新强化不同课程知识点之间的关联性，将它们融合在一起讲授，这就是“跨课程融合教学”的理念。

二、可行性分析

传统的数学学科发展过程，其实是一个“分”的过程。且不说数学各个分支的产生，就说同济版线性代数其实就是在1978年从高等数学课程中分解出来后（原为高数第13章），发展为一门独立的课程。这个过程反映出两个事实：其一是这些课程之间存在着紧密的联系;其二是课程内容在的不断扩充与细化。第一个事实为“课程融合教学”提供了理论依据，这些课程原本就是一个整体。第二个事实则是课程不断“分”的主要原因之一，也是我们对课程进行“合”时，需要面对的困难——随着知识点的增加，在有限的课时内讲清楚本课程的知识点已经不容易了，如何能兼顾到其他课程的内容？

要回答这个问题我们可以从两个方面讨论：

1.讲授其他课程内容真的会降低效率吗？我们进行了两年的教学实践，比如说将线性代数中“向量组的线性相关性”和高等数学中“向量及线性运算”的内容整合到一起讲授，或是将离散数学中一阶逻辑部分的换名规则引入高等数学中讲解“微分形式不变性”“换元积分法”等知識点。我们甚至将高等数学中的函数概念与计算机编程里面的函数概念进行对比。结果发现，初始部分章节内容的课时会变得更加紧张。但在这个过程中，学生对知识点理解的深度和广度都大大增加，可以非常灵活地运用这些知识点。而且学生可以将各知识点联系起来，对整个课程体系有一个非常全面的了解，构造出一个知识体系。然后在后续学习中不断自发地将新的知识点与已经掌握的知识点进行比较，自动合并类似知识点，关联相关知识点，不断完善自己的知识体系，从而极大地提高了课程的后半段以及后续课程的学习效率。因此，从总体来看，课程融合会提高而不是降低教学效率，它可以有效避免不同课程间存在的类似知识点的重复讲解。

2.2018年我国教育部发布了《教育信息化2.0行动计划》，提出“坚持信息技术与教育教学深度融合的核心理念，坚持应用驱动和机制创新的基本方针，建立健全教育信息化可持续发展机制，构建网络化、数字化、智能化、个性化、终身化的教育体系。”[2]随着MOOC和SPOC等线上教学或线上线下混合式教学模式的出现和普及，以及“超新泛雅”等网络课程平台功能的不断完善，教学模式正在发生巨大的变化。教学的时间、地点甚至内容都不再局限于以往的传统课堂。在这些新的技术和教学模式下，教与学的关系已经发生了改变。教学的主体是学生，他们可以通过课程平台去主动检索，吸收他们需要的知识，老师起的作用是引导和解惑。借助网络课程平台，我们可以轻易地突破以往不同课程之间的壁垒，改变不同课程间界限分明、互不联通的弊端。让不同课程的教学内容、教学方法横向交叉渗透，优化网络课程教学活动，支持学生跨课程的网络学习，实现数学学科跨课程教学内容的互相补充[3]。目前很多高校都在建设“自然科学导引”“社会科学导引”等网络课程体系，就是利用课程平台强化相关课程之间的联系，帮助学生构造完整的知识结构。在这样的情况下，实现“跨课程融合教学”是完全可行且有必要的。

三、教学实例

线性代数第四章“向量组的线性相关性”，主要讲解向量的运算及相互关系，进而拓展到向量组、线性方程组求解和限量空间。这里，向量的定义和向量的运算是基础概念，但在线性代数课程中，所有问题都由公式来进行定义和推导，没有图形。因此可以在这里引导学生在网课平台上学习高等数学第八章第一节“向量及其线性运算”的内容，作为“形”的补充，从而达到“数形结合”的教学效果，帮助学生快速、深刻地理解线性相关等概念。

线性代数中对向量的定义为“n个有次序的数a1，a2，…，an所组成的数组称为n维向量”[4]。高等数学中对向量的定义为“有大小，有方向的量”[5]。同时也通过空间直角坐标系定义了“有序数x，y，z称为向量的坐标，记作=（x，y，z）”[6]，这样就达到了形与数的统一。有序数的个数，对应着向量所在空间的维度，这个概念可以从二元向量扩展到三元再进一步扩展到n元向量。

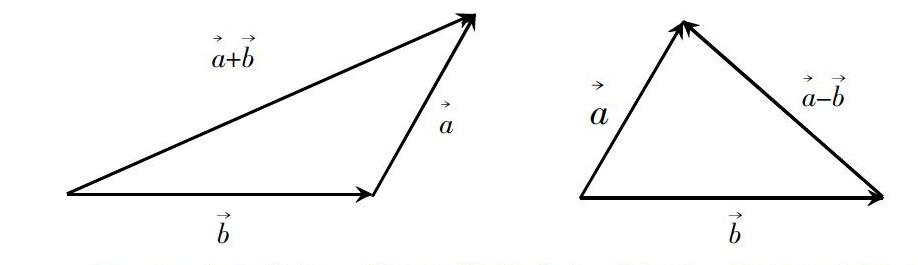
然后在讨论课中，利用高等数学中对向量运算的几何解释（如图），指导学生分组依次讨论如下概念。

1.两向量、线性相关，在线性代数中意味着向量能由向量线性表示，=k。而这个等式在高等数学中表示两向量平行，按向量可任意平移的特点，也可理解为两向量是共线的。

2.类似的，三个向量线性相关，即向量可以由向量、线性表示为=k1+k2（k1，k2≠0），在高等数学中意味着三个向量共面，也就是向量含在向量、所构成的平面（二维空间）内。

3.线性代数中向量组A的秩R（A）为A的一个最大线性无关组所包含向量的个数r。结合前两个讨论的结果，我们可以知道最大无关组中任何一个向量i都不在其余（r-1）个向量构成的空间内，因此r这个向量可以构成一个r维的空间。那么我们就理解了向量组的秩R（A）表示了向量组所有向量所能构成的最大空间维度。

4.线性代数中的“向量空间”就和高等舒徐中的n维空间结合对应上了，而空间直角坐标系就是一个典型的正交向量组，也是向量空间的一个基。我们也可以讨论除了直角坐标系外，是否还有其他的坐标系——坐标系转换。

5.这样一来，线性方程组的解的结构也可以用高等数学中平面的概念来帮助理解。先看三元方程组，方程组中每个方程ai1x1+ai2x2+ai3x3=di对应到平面方程Ax+By+Cz+D=0，从而线性方程组求解从图像上就可以理解为求几个平面的交集。交集可能是一个点、一条线、一个面或是不存在，分别对应线性方程组的解空间是零维、一维、二维或是无界，这样也可以解释通解中向量的个数。然后拓展到n维空间，超平面相交的情况。

如此，线性代数中诸多抽象的概念变成解析几何中可见的图形，让学生有了直观的感受。高等数学中的几何内容部分，也有了更多的算法支持。通过两年的教学测试，这样的教学方式由于做到了“数形结合”，便于学生理解并加深了印象，总体教学效果、效率得以提升。同时还帮助学生将线性代数和高等数学两门课程有机结合起来，形成了一个完整的知识体系，使学生对知识的运用更加灵活自如。

四、后记

“兼容并包，万物并育”是中华民族在几千年的文明历程中总结出来的智慧。随着人们对世界的不断探索，掌握知识的不断累积，我们需要学习的东西也会越来越多。单单依靠“分”是不能解决问题的，我们要更多地思考“通”的问题，要对这些知识进行融合，找到它们共同的、最本质的那些东西。只有这样，我们才能在不断改革中提高教学的效率、效果，形成完整的、巩固的知识体系，才能真正学以致用。

這个过程对老师也提出了更多的要求。比如需要老师进一步增加自己的知识储备，除了“专”以外，还需要足够的“博”;需要随时掌握新的信息、多媒体及网络技术，做到与时俱进;需要不断探索，改进教学设计，进行大量的调研和实践;需要打造一个分工有序，稳定的教学团队，以实现更复杂多样的教学方案等。

习近平总书记指出，“当今世界正经历百年未有之大变局”，这是挑战也是机遇。传统教学模式已经不再适应正在快速发展的社会经济形势，我们需要给学生打造一种更开放、更自由、更高效、更系统的学习模式。而课程融合教学，将会是实现这些需求的一种有效方式。

参考文献：

[1]蒲晓妮.高职院校软件技术专业跨课程教学项目研究与探讨[J].兰州石化职业技术学院学报，2018（3）.

[2]教育部.教育信息化2.0行动计划[EB/OL].2018-04-18[2019-05-02].http：//www.moe.gov.cn/srcsite/A16/s3342/201804/

t2018425_334188.html.

[3]吴霞，巴寅颖，王星，等.基于BB平台的中药化学网络课程建设与跨课程学习的促进[J].继续医学教育，2017（1）.

[4]同济大学数学系.线性代数[M].6版.高等教育出版社，2014：81.

[5]同济大学数学系.高等数学（下册）[M].7版.高等教育出版社，2014：1.

[6]同济大学数学系.高等数学（下册）[M].7版.高等教育出版社，2014：7.

◎编辑 马燕萍