基础设施REITs市场风险度量

牛耘诗 伍迪 王守清 叶露

近年来，随着我国城镇化建设的不断推进，基础设施建设领域的资金需求持续增长。基础设施项目的一级市场投资具有单笔投资量大、回报周期长、收益风险高等特征，对投资者的要求较高，导致传统融资模式逐渐无法满足庞大的基础设施资金需求。通过资产证券化、股权交易、再融资等方式构建完善的基础设施二级市场，有助于盘活存量资产、提高资产流动性、建立基础设施资金流入和退出的有效循环体系。REITs作为不动产资产证券化的一种重要手段，为中小投资者提供了投资基础设施项目的机会，可以有效盘活存量资产、优化企业资产负债表、分散基础设施投资风险，与基础设施二级市场属性契合度极高。因此，基础设施REITs或将成为解决我国基础设施项目融资难、发展基础设施二级市场、增强资产流动性的重要创新举措之一。

基础设施REITs的底层资产是以使用者付费模式为回报机制的基础设施项目。由于此类项目市场化水平较高、商业模式相对成熟，政府一般不會提供担保或补助，但是这类项目的市场需求和收入水平往往可预测性较低，导致项目的未来收益波动风险较大。以高速公路项目为例，其主要收入来源于车辆通行费。由于项目具有公共属性，导致收费受到政府和行业部门管制，虽然价格水平保持相对稳定，但未来的交通流量预测难度较大，且存在政策风险、替代品风险等风险。若要对其开展标准REITs，建立合理有效的风险管控机制是十分必要的。

基础设施REITs交易中，辨识收益率波动特征、测量金融风险是金融主管部门和监管机构关注的重点，也是推广REITs产品不可缺少的环节。为进一步探索基础设施REITs运作模式的科学性、合理性，本文尝试对基础设施REITs的风险进行度量，并对指定的持有期风险进行预估，以期为基础设施REITs风险度量工具的创建提供理论支持，并为我国基础设施REITs的推广和应用提供参考。

REITs风险度量模型选择

金融市场风险度量主要有两种思路。一种思路是测定产品价值和市场因子变化之间的关系，如证券系统性风险指标β系数、期权风险指标Delta值、债券利率风险指标久期和凸性。该思路实质上是测量金融资产价值对市场因子的敏感程度，优点是可以直观反映资产价值相对于市场风险的变化量，但同时也存在单个指标的使用范围狭窄、测量偏向局部、不稳定性较高等缺陷。另一种思路则是用方差和标准差来衡量证券收益的波动性，但该思路也存在将正向偏差计入风险、难以明确指出资产组合损失等缺陷。

REITs风险度量的核心是价格波动性的估计和预测。20世纪90年代以来，在险价值（Valueat Risk，VaR）成为巴塞尔银行监管委员会、美国联邦储备银行等众多金融机构认可的度量金融风险、进行风险管控的重要工具。VaR实质上是指在一定置信水平下持有某种金融资产一段时间后可能遭受的损失单边临界值，其最大优点在于能够准确测量并直观反映不同风险源及其相互作用产生的损失。同时，VaR是一种基于下方风险（Downside-Risk）思想建立的风险度量方法，它只考察收益率概率分布的左边，即只测量位于期望之下的那部分收益，更符合投资者的心理感受。Lu、张红、邬玉婷等学者分别运用VaR模型对中国香港、澳大利亚、英国、美国等REITs市场风险进行了度量和预测，结果较为理想。

VaR有多种计算方法，主要包括以历史模拟法、蒙特卡洛模拟法为代表的非参数估计方法和以风险计量（Riskmetrics）模型、方差—协方差法为代表的参数估计方法。金融市场的数据往往具有“尖峰厚尾”的特征，在某一段时间内剧烈波动，而在另一段时间内变化平缓，这种波动性集聚的现象导致传统VaR计算方法均存在一定的缺陷。例如，基于正态分布假设的方差——协方差法往往会低估实际风险价值；历史模拟法完全依赖历史数据集合并假设收益率分布在样本期限内固定不变，对历史数据中没有包含的风险无法预测；蒙特卡洛模拟法则依赖特定的随机过程，可能存在模型风险。

针对以上问题，罗伯特·恩格尔（Robert Engle）最早提出可以用自回归条件异方差（Autoregressive Conditional Heteroskedasticity，ARCH）模型来更好地预测金融时间序列的方差，托本·波勒斯列夫（TorbenBollerslev）在ARCH模型的基础上进一步提出了广义ARCH（Generalized ARCH，GARCH）模型。近年来，利用GARCH等不同金融计量模型对金融资产收益率波动进行建模分析和预测得到了广泛应用，其中，约翰·科特（John Cotter）和西蒙·史蒂文森（Simon Stevenson）基于多变量GARCH模型对REITs不同子行业收益和波动率的相关关系进行了研究，取得了一些成果。

本文将基于VaR理论建立GARCH模型，试图更准确地模拟基础设施REITs收益率的实际风险特征，从而有效评估基础设施REITs的风险水平，为创建统一的基础设施REITs风险度量工具提供参考。

GARCH-VaR模型构建

VaR定义为，在给定的置信区间内，由于市场价格变动所导致的持有期内最大预期损失，即：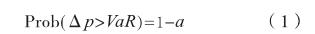

其中，为某一金融资产持有期间的损失值，表示在给定置信水平下的在险价值，即可能的损失上限。

ARCH（p）模型在一般的线性回归模型上考虑了方差的波动性集聚现象，假设当期的方差依赖于前p期扰动项的平方，即：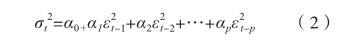

ARCH（p）模型在p值较大的情况下需要估计很多参数，会造成样本容量损失，而GARCH模型的待估参数较少，可以更为精确地估计方差。GARCH（p，q）模型是在ARCH（p）模型基础上的拓展，加入了的自回归部分，公式如下：

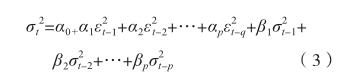
其中，p表示的自回归阶数，q表示扰动项平方的滞后阶数。

进一步，可以得到t时的VaRt计算公式如下：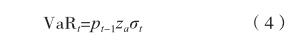

其中，pt-1为前一日REITs收益指数价格，Za指置信度α为时对应的分位数，σt为t时收益样本的标准差。

在某种意义上，GARCH（1，1）模型等价于无穷阶的ARCH模型。因此，我们常可用GARCH（1，1）模型来简化ARCH（p）模型对序列方差进行估计。

基础设施REITs风险度量

研究思路

本文选取VaR作为指标，从微观角度对基础设施REITs的市场风险进行定量研究。首先，利用GARCH（1，1）模型来模拟基础设施REITs收益率的条件方差序列，并检验模型是否能很好地消除原来序列存在的“尖峰厚尾”特征；其次，将各期条件方差的值代入式（4）中测算出基于观察样本预测的风险值VaR；最后，将预测的VaR与实际损益进行对比，检验风险度量模型的有效性。

模型变量统计分析

本文采用美国基础设施REITs日收益率作为样本数据进行实证分析，其波动图，如图1所示。选择2012年1月1日—2016年12月31日作为观察区间建立GARCH-VaR模型，并以此对2017年1月1日—2018年12月31日的日收益率进行预测，再与实际情况进行对比分析，并进行模型的稳健性检验。

基础设施REITs日收益率的描述性统计结果，如表1所示，从偏度和峰度值可以看出序列具有“尖峰厚尾”的特征。从哈尔克—贝拉（Jarque-Bera，JB）统计量结果来看，基础设施REITs日收益率序列不服从正态分布。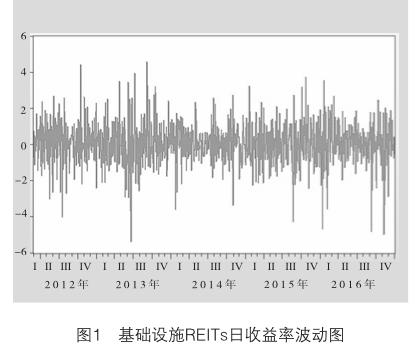

实证分析过程

平稳性单位根检验

对基础设施REITs日收益率序列进行平稳性单位根（Augmented Dickey-Fuller，ADF）检验，检验结果，如表2所示。这说明，基础设施REITs日收益率序列Yt不存在单位根，是平稳序列。

ARCH效应检验

以上分析表明，基础设施REITs的日收益率序列存在波动性集聚。作为对照，我们首先建立自回归（Auto Regressive，AR）模型，用赤池信息准则（Akaike Information Criterion，AIC）确定自回归模型的阶数为4，对AR（4）模型的残差进行相关性检验的结果，如表3所示。

从表3的检验结果可知，残差平方的Q统计量的P值均小于0.01，说明在1%的显著水平下，拒绝残差平方不存在自相关的原假设，故扰动项存在条件异方差，即波动性集聚。

进一步，对序列残差进行ARCH-LM（Lagrange Multiplier，拉格朗日乘數）检验，检验结果，如表4所示。

从检验结果来看，F统计量和LM统计量的伴随概率P值都为零，说明基础设施REITs日收益率序列存在ARCH效应。因此，若要消除条件异方差的影响，需要进一步构建ARCH或GARCH模型。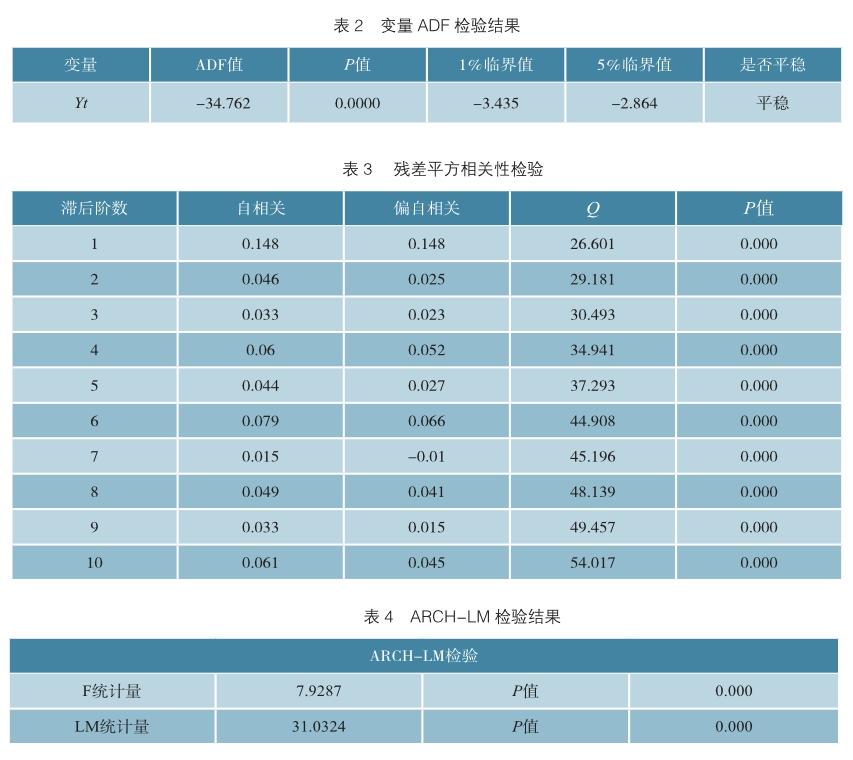

建立模型

在模型的选择上，本文选择ARCH（1）与GARCH（1，1）模型进行对照，如表5所示，依据AIC与施瓦兹准则（Schwarz Criterion，SC）选择最适合的模型。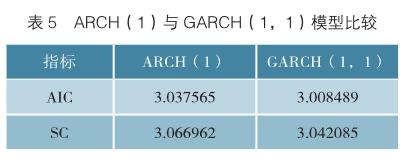

由表5可知，GARCH（1，1）模型AIC与SC值更小，因此本文选择GARCH（1，1）模型进行风险度量。对建立GARCH模型后的残差序列进行LM检验，证实异方差效应被消除。

在构建GARCH模型时，需要选择合适的随机误差项分布函数，对在正态分布下构建的GARCH（1，1）模型扰动项的正态性进行检验，JB统计量为197.96，伴随概率P值为0，说明扰动项拒绝服从正态分布的原假设。为此，本文选取常用的T分布和广义误差分布（Generalized Error Distribution，GED）模拟随机误差分布，并对拟合残差结果进行LM检验，确认了模型可以很好地消除ARCH异方差效应。根据信息准则对比三种分布构造的GARCH模型，如表6所示。

由表6结果可知，T分布下的AIC值和SC值均为最小，所以最终选择T分布对残差序列进行模拟。拟合方程为GARCH = 0.0800171557301 + 0.0863831857834×RESID（-1）^2+ 0.852899491643×GARCH（-1），各项系数均显著，拟合结果，如图2所示。

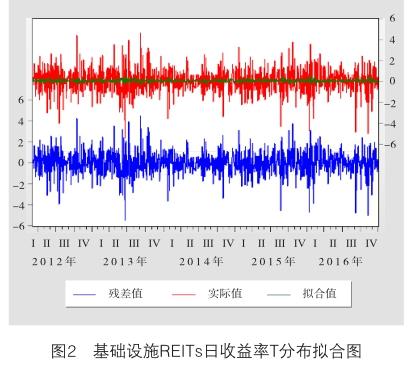
拟合方程中的ARCH项和GARCH项系数皆为正，验证了基础设施REITs日收益率序列具有波动性集聚的现象，前期较大的冲击波动会对后期产生影响。ARCH项和GARCH项系数之和接近1，说明条件方差序列具有记忆性，收益率的波动性具有较长的持续性。其中，GARCH项系数要明显大于ARCH项系数，说明市场自身的记忆性要强于外部冲击对于REITs收益波动性的影响。由图2还可知，T分布GARCH（1，1）模型拟合的残差序列（残差值）走势与实际的收益率（实际值）走势保持高度一致，拟合效果较好。至此，本文依据2012年1月1日—2016年12月30日的基础设施REITs日收益率数据建立了GARCH（1，1）模型以模拟序列方差的波动情况。

VaR计算

利用上文创建的GARCH（1，1）模型预测2017年1月1日—2018年12月30日基础设施REITs的收益方差，代入式（4）后，可以得到置信水平分别为95%和99%下的VaR值，与基础设施REITs实际当日损益的对比，如图3所示。结果显示，REITs的实际当日损益只有少数几次超过估计的95%VaR值，几乎不会超过99%VaR值，模型的预测效果较好。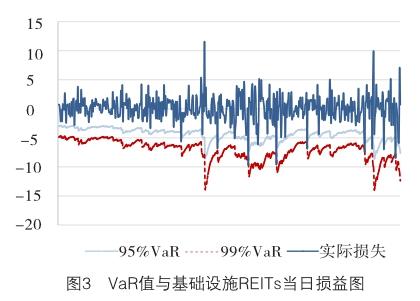

稳健性检验

库皮克（Kupiec）似然比（Likelihood Ratio，LR）检验通过给出失败次数接受区间来判定VaR的风险度量是否有效，其统计量LR服从自由度为1的卡方分布，定义公式如下：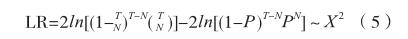

其中，N为失败次数，即评价样本实际损失值大于给定VaR的次数；T为实验样本数量；P= 1 ？α，α为给定的置信区间。

对本文建立的GARCH（1，1）模型进行库皮克检验，如表7所示，利用矩阵实验室（Matlab，一种商业数学软件）计算参数T=500天、置信度α分别为95%和99%下LR失败次数的理论值区间，并与实际的失败次数作对照。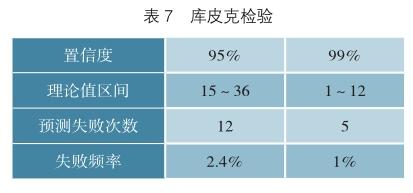

由表7结果可知，在95%置信水平下，模型预测的失败次数小于理论值区间，预测失败率为2.4%；在99%置信水平下，模型预測的失败次数也在理论值区间内，预测失败率为1%。所以，预测的VaR通过了稳健性检验，说明本文建立的GARCH（1，1）模型能有效预测基础设施REITs收益率的波动风险。

结语

本文旨在研究基础设施REITs的风险分布特征，并建立合理的模型对风险进行预测与监控。本文首先利用GARCH（1，1）模型对基础设施REITs的收益波动特征进行模拟，验证结果表明，模型能很好地消除异方差效应；然后运用VaR方法测算了基础设施REITs的风险值，预测的VaR能有效模拟收益序列的实际损失。实证分析结果表明，本文建立的GARCH-VaR模型能够有效评估基础设施REITs的风险水平。

成熟的REITs市场中，建立有效的市场风险度量工具是十分必要的，一方面为REITs投资者提供投资风险预测的依据，另一方面有利于REITs产品的标准化与市场化发展。我国基础设施REITs市场可以参考本研究结果，建立统一的REITs市场风险度量工具，从而完善基础设施REITs的风险管控制度，提高监管水平，促进REITs市场的稳定、健康发展。P

牛耘诗，博士，中国国际工程咨询有限公司研究中心工程师。

伍迪，博士，中国国际工程咨询有限公司研究中心高级工程师、副处长。

王守清，博士，清华大学建设管理系教授，清华大学PPP研究中心首席专家。

叶露，清华大学建设管理系/清华大学恒隆房地产研究中心硕士研究生。

【注：本文基于国家自然科学基金资助项（71772098和71572089）】