CVDA序贯采样法在全铝车架轻量化设计上的应用*

王哲阳，王震虎，张松波，李落星

（1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082； 2.湖南大学机械与运载工程学院，长沙 410082；3.重庆长安汽车欧尚研究院，重庆 400023）

前言

由于汽车各性能之间的相互影响与制约，多目标、多学科优化方法在近几年已广泛应用于解决各种工程问题中［1-2］。然而由于优化时的反复迭代导致CAE模型计算时间较长，使整个优化过程需要付出昂贵的计算代价。为解决该问题，设计人员通常使用近似模型来代替有限元模型。近似模型的建立往往需要采集大量的样本点，这就导致计算量同样巨大而不能满足项目进度要求，序贯采样法运用较少的样本点建立高精度的近似模型，能大大提高计算效率从而很好地满足项目进度要求。

序贯采样法的关键在于如何根据初始样本点信息确定新增样本点在设计空间中的位置，国内外学者对此进行了一系列的研究。Currin和Sacks等［3-5］针对Kriging近似模型提出最大熵、MSE和IMSE 3种方法来定位新增样本点位置，但以上3种方法只适用于Kriging近似模型，不具有普遍性。Johnson等［6］提出以最大距离法（maximin distance approach，MDA）来判断新增样本点位置，该方法实现了样本点在样本空间中的均匀分布，但是对于局部波动大的问题预测效果不佳。Jin等［7］在Johnson的基础上提出了最大比例距离法（maximin scale distance approach，MSDA）与基于交叉验证的均方根误差法（cross-validation approach，CVA），前者是对最大距离法的修正，但其寻找新样本点时并未使用初始近似模型的信息，采样效果同样偏向于样本点在样本空间中的均匀分布，后者使用交叉验证的方式来预测近似模型在任意一点的误差，但在对任意一点的预测过程中，该点越接近交叉验证时去除的样本点，它的预测精度就越比实际精度低［8］，这会使寻优出的响应误差最大样本点位置与某一初始样本点接近甚至重合，产生样本点聚集现象。文献［7］、文献［9］和文献［10］通过增加距离约束来防止样本点聚集，但是距离约束的阈值如何确定并无有效方法。本文中参考CVA法的寻优思路，针对交叉验证导致的近似模型局部精度验证偏低问题，引入样本点距离参数对其进行修正，提出了一种新的序贯采样法—CVDA法，并通过测试函数将CVDA法与另外多种采样法进行对比，体现CVDA法的优越性。最后基于一款全铝车架对其弯扭刚度、弯扭模态等性能采用CVDA采样建立近似模型并进行轻量化设计。

1 序贯采样法

1.1 序贯采样法流程

序贯采样法本质上是一个再采样以提升近似模型精度的过程，而精度提升的效果取决于新增样本点在设计空间中的位置。一般来说，新增样本点位于设计空间的平坦区域，则对近似模型精度的影响不大，新增样本点位于设计空间中波动较大区域，会有助于近似模型的精度提升。序贯采样法流程如图1所示。

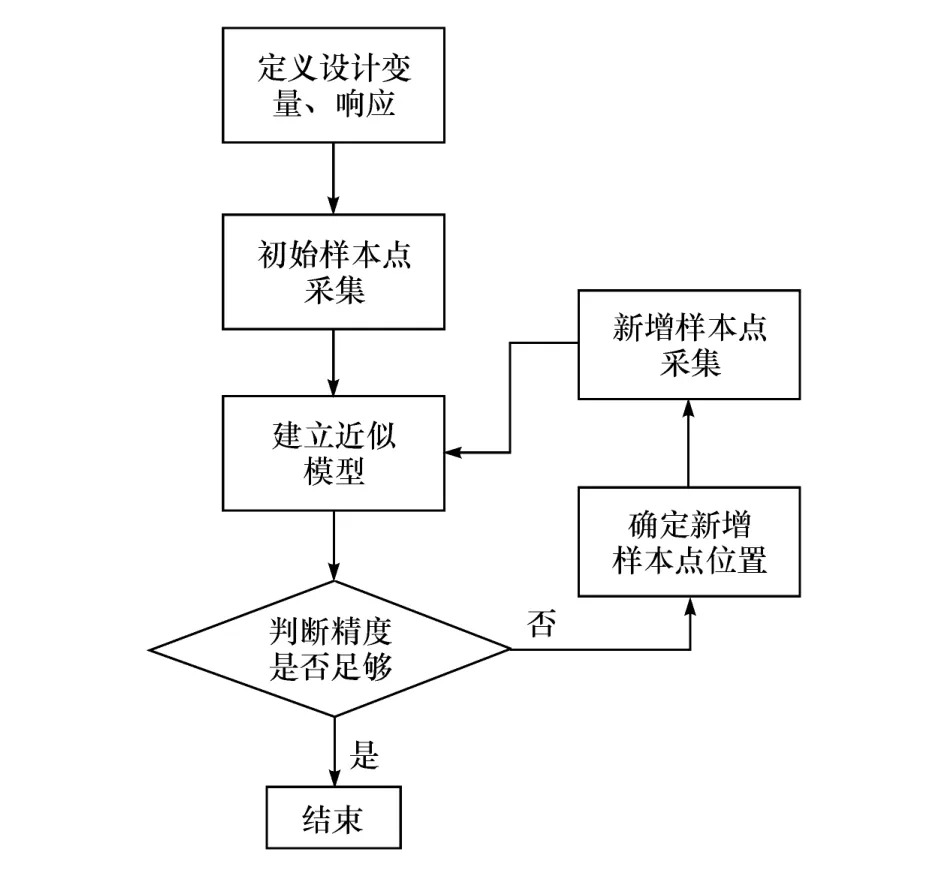
图1 序贯采样流程图

1.2 序贯采样法原理

对于如何确定新增样本点位置，国内外已经有了一定的研究，较为经典的有最大距离法、最大比例距离法和基于交叉验证的均方根误差法等。

1.2.1 最大距离法（MDA）

Johnson等［6］提出了关于最大距离法的标准，基于已存在的样本点集XP，使新加入的样本点XC距离已存在最近样本点的距离最大，即

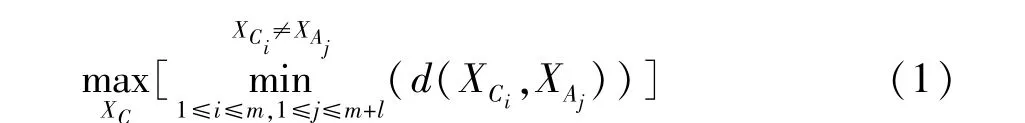
式中：XAj∈XA＝XC∪XP，XA为总样本集，XAj为XA中的第j组样本点；XCi为新增的第i组样本点；m为新增样本点个数；l为初始样本点个数。

1.2.2 最大比例距离法（MSDA）

最大比例距离法［7］是对最大距离法的修正，考虑各设计变量对响应贡献量的大小，对设计变量之间的距离公式进行修正，认为高贡献量的设计变量有更大的比例系数ah，数学模型为

式中：ah为第h个设计变量对响应的灵敏度值；vh为第j个已有样本点中第h个设计变量的值；wh为第i个新增样本点中第h个设计变量值。

1.2.3 基于交叉验证的均方根误差法（CVA）

Jin等［7］提出采用留一法交叉验证的方式来预测近似模型在任意一点x处的误差。其值通过交叉验证下误差均方根e（x）来估计，即

式中：y-i（x）为去除第i个样本点后的样本集建立的近似模型在x处的估计值；y（x）为通过已存在所有样本点建立的近似模型在x处的估计值；n为已有样本点个数。以e（x）最大为目标对x进行寻优，结果即为新增样本点的位置。

1.3 CVDA序贯采样法

考虑到交叉验证时去除点与新增样本点x之间因为距离不同而导致的对预测误差值的影响，提出一种新的序贯采样法（CVDA）：引入距离比例系数ωi，当x距离去除点越近时，ωi的值越小，以此来解决因为去除样本点所导致的局部精度降低的问题，数学模型为

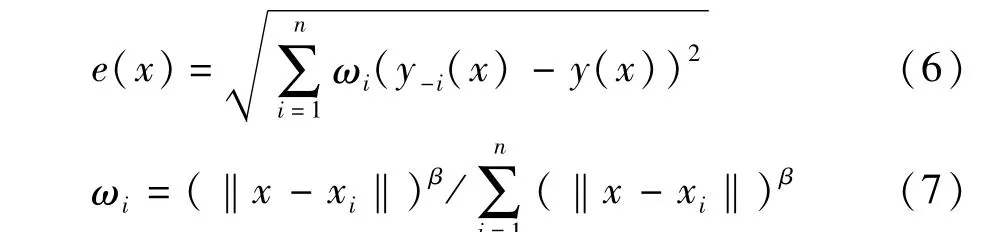
2 数学算例

为能更直观地对比各采样方法新增样本点在设计空间中的位置，展现CVDA序贯采样法能更为准确地将新增样本点定位到近似模型精度低区域的能力，在这部分中，选取一维测试函数Farhang Mehr，以确定性系数R2作为评价近似模型精度的指标，对CVDA法的有效性进行验证，且与其他采样方法包括最优拉丁超立方［11］（OLHD）、MDA、MSDA和CVA等进行对比。其中，由于设计变量只有一个，所以MDA法与MSDA法在本例中效果相同。测试函数的解析式为

该函数在（0，0.4）范围内变化较剧烈，而在（0.4，1.0）的范围内变化较为平缓。首先，使用OLHD法选取11个样本点，11个样本点均匀分布在（0，1）的区间范围内，采用径向基神经网络建立近似模型，预测精度初始值为0.787，样本点在设计区间内的分布如图2所示。可以看出，在高波动区域（0，0.4）中，近似模型预测精度很低。

图2 初始样本点分布图

图3 （a）～图3（d）表示分别采用OLHD、MDA、CVA和CVDA 4种采样方法新增样本数至21个时的预测效果图。其中OLHD为非序贯采样方法，在新增样本点过程中初始样本会随之改变，MDA、CVA和CVDA为序贯采样法，在新增样本点的过程中初始样本不变，预测精度采用1 000个额外样本点进行验证。

由图3（a）～图3（c）可以看出，OLHD与MDA采样方法讲究样本点在设计空间中的均匀分布，不能将新增样本点很好地定位到函数波动大、近似模型精度低的区域。CVA法由于其本身的局限性，新增样本点与初始样本点产生聚集现象，对近似模型实际精度并无太大提升效果。从图3（d）中可以看出，根据CVDA法计算出的新增样本点大多在局部波动较大的（0，0.4）范围内，并与函数值的波峰、波谷有一定的重合度，预测精度提升明显。

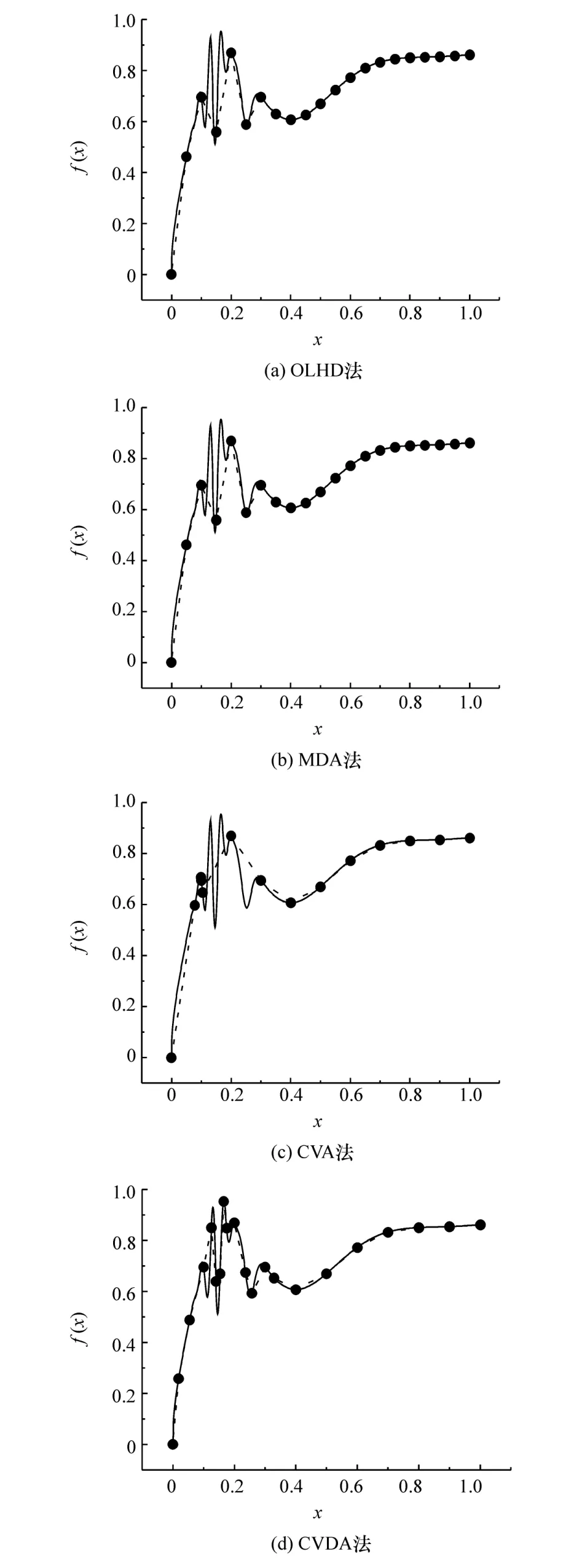
图3 21个样本点的预测效果对比

4种采样方法采样建立的近似模型预测精度变化如表1所示。

表1 4种采样方法近似模型精度变化

由表1可以看出，经过10次序贯采样后，使用CVDA法采样的近似模型精度从0.837增加到了0.950，增幅13.5%，较通过OLHD、MDA和CVA 3种采样方法采样而建立的近似模型预测精度分别高出11.1%，11.1%和30.3%。由此可以得出结论，与其余3种方法相比，CVDA法可以使用更少的样本点建立更高精度的近似模型。

3 铝合金车架仿真建模与精度验证

3.1 有限元模型的建立

车架主要由铝合金型材焊接而成，因此建立的有限元模型具有以下特征：（1）型材采用shell单元进行模拟，赋予相应的材料与属性，面与面之间共节点连接；（2）综合考虑计算的精度和效率，网格的基本尺寸采用5 mm；（3）铝型材之间的MIG保护焊采用shell单元进行模拟，具体模拟方式见图4。由此得到铝合金车架有限元模型，如图5所示。其中网格节点794 281个，壳单元个数共808 652个。

MIG保护焊的模拟参数：

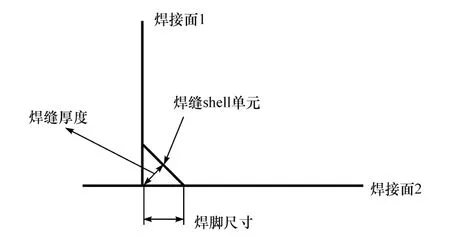
图4 MIG保护焊模拟方式

图5 铝合金车架有限元模型

式中t1和t2分别为两焊接面的厚度。两焊接材料中屈服强度较小的一方作为焊缝的材料。

3.2 有限元模型的精度验证

通过对比有限元车架模型与实际车架的弯扭刚度、弯扭模态等性能来验证有限元模型建模的可靠性。

3.2.1 弯曲刚度仿真与测试

约束前后台架左右底部X，Y，Z 3个方向的平动和转动自由度，在两边门槛中部各垂直向下加载1 000 N的作用力。弯曲刚度的计算公式为

式中：F为施加载荷，N；Z1，Z2分别左右测点的Z向绝对位移，mm。

弯曲刚度的仿真云图和实验现场如图6和图7所示。

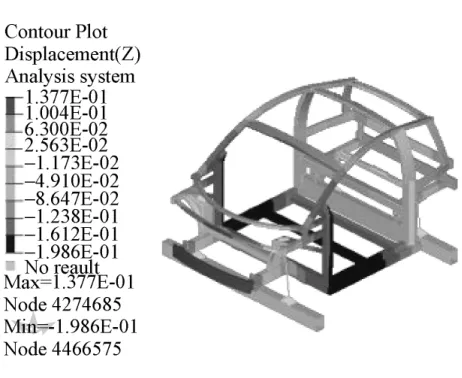
图6 弯曲刚度位移云图

图7 弯曲刚度实验

3.2.2 扭转刚度仿真与测试

约束台架中部X，Y，Z 3个方向的平动自由度，约束台架后端左右两边底部X，Y，Z 3个方向的平动和转动自由度。在台架前端左侧施加2 000 N的作用力。扭转刚度的计算公式为

(1)在304L不锈钢基体中添加了1%～7%的FeCrBSi作为烧结助剂，在烧结温度为1340 ℃时，试样的烧结密度随着FeCrBSi添加量的增加而升高，但孔隙度逐渐降低．当添加量为3%～5%时，烧结密度达到7.80～7.85 g/cm3．

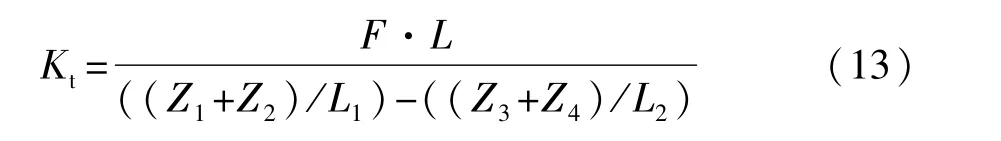
式中：F为施加载荷，N；L为加力点到台架左侧支撑点的距离，mm；Z1～Z4为4个测点的Z向绝对位移，mm；L1，L2分别为测点1与2和3与4的间距，mm。

扭转刚度的仿真云图和实验现场如图8和图9所示。

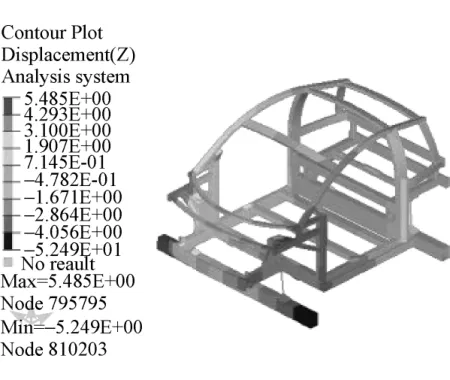
图8 扭转刚度位移云图

图9 扭转刚度实验

3.2.3 模态仿真与测试

采用Lanczos法计算白车身的各阶模态和振型，频率范围为1-100 Hz，根据模态振型提取白车身的1阶弯曲和1阶扭转模态，模态实验如图10所示。

图10 模态实验图

表2为有限元模型弯扭刚度、1阶弯扭模态仿真值与实车实验值的对比。模型误差均控制在10%以内，表明铝合金有限元车架模型能用于项目详细设计阶段的性能评估与优化。

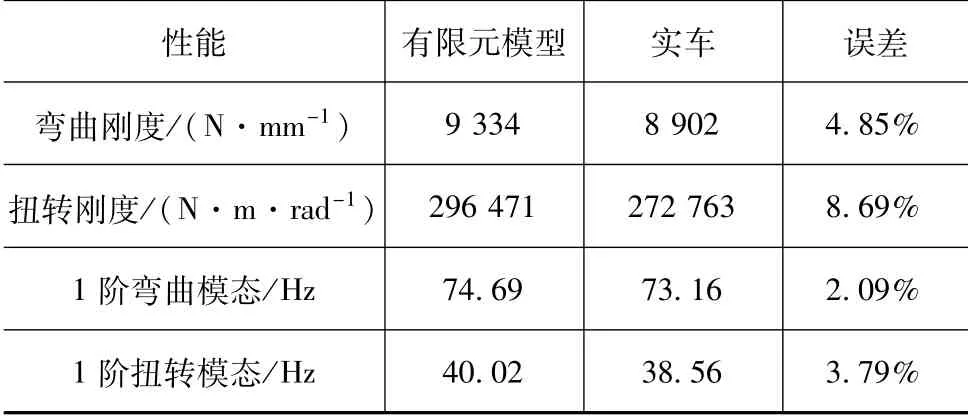
表2 有限元模型仿真值与实验值对比

4 基于CVDA序贯采样的多学科优化

4.1 基于CVDA法近似模型的建立与精度对比

首先通过灵敏度分析挑选出对称的17根梁作为本次优化的主要部件，优化部件如图11所示，共有壁厚变量12个。

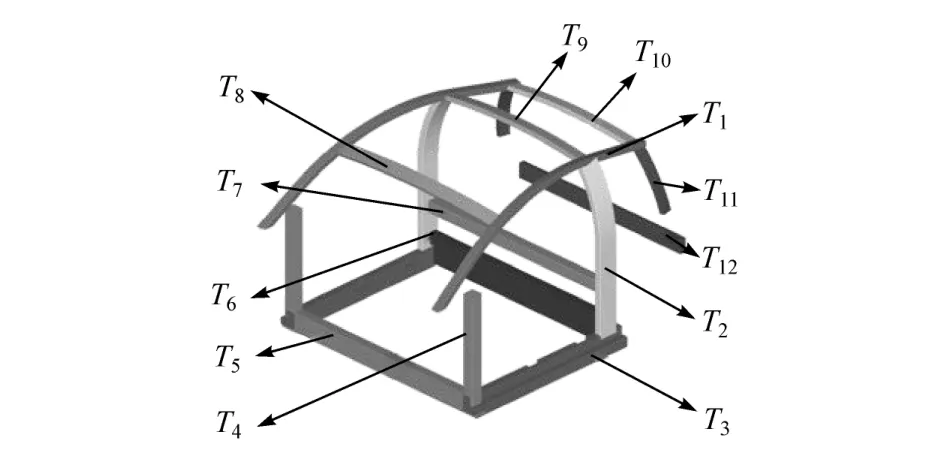
图11 设计变量图

首先使用OLHD法抽取弯扭刚度工况和质量性能初始样本点26组，弯扭模态工况初始样本点50组，通过RBF神经网络进行近似模型拟合，得出预测精度R2分别为0.917，0.939，0.989，0.772和0.779。由于质量性能预测精度已经很高，不需要再新增样本点。

分别对弯扭刚度、弯扭模态4种工况进行基于CVDA法的序贯采样。刚度工况精度达到0.98，模态工况精度达到0.9时采样停止，并与OLHD、MDA和CVA法进行对比来验证该方法在工程应用上的可行性。4种工况精度提升如图12～图15所示。

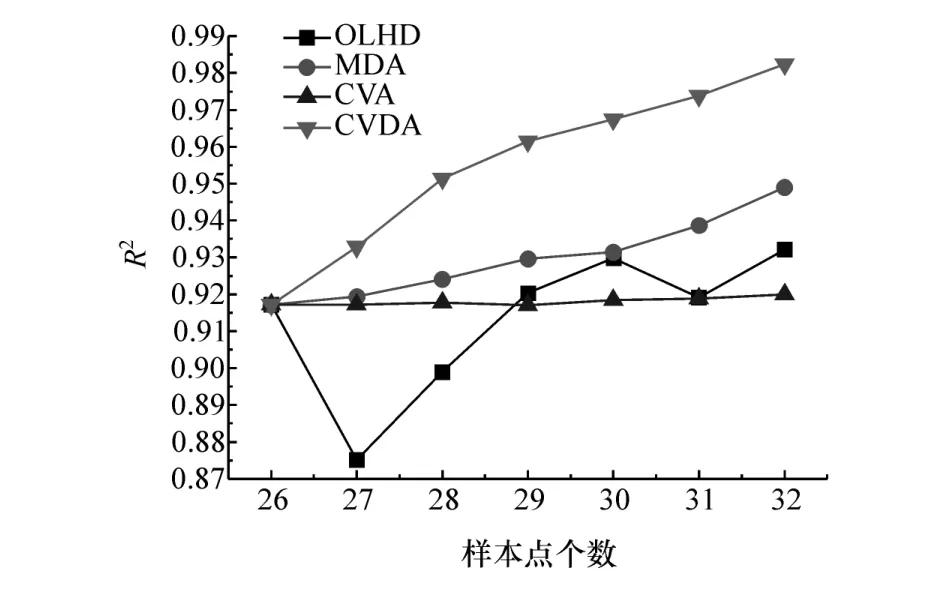
图12 弯曲刚度近似模型精度增长对比

图13 扭转刚度近似模型精度增长对比

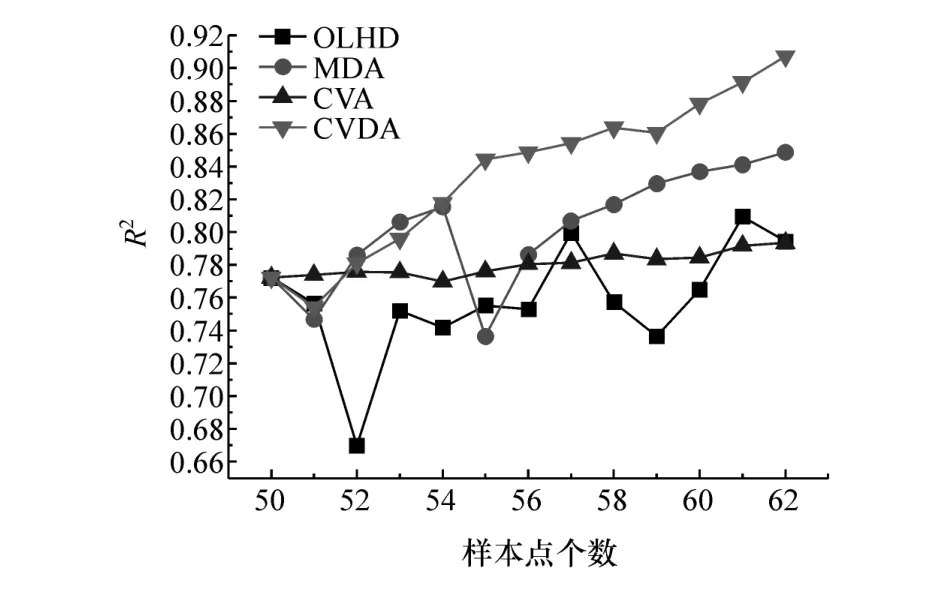
图14 弯曲模态近似模型精度增长对比

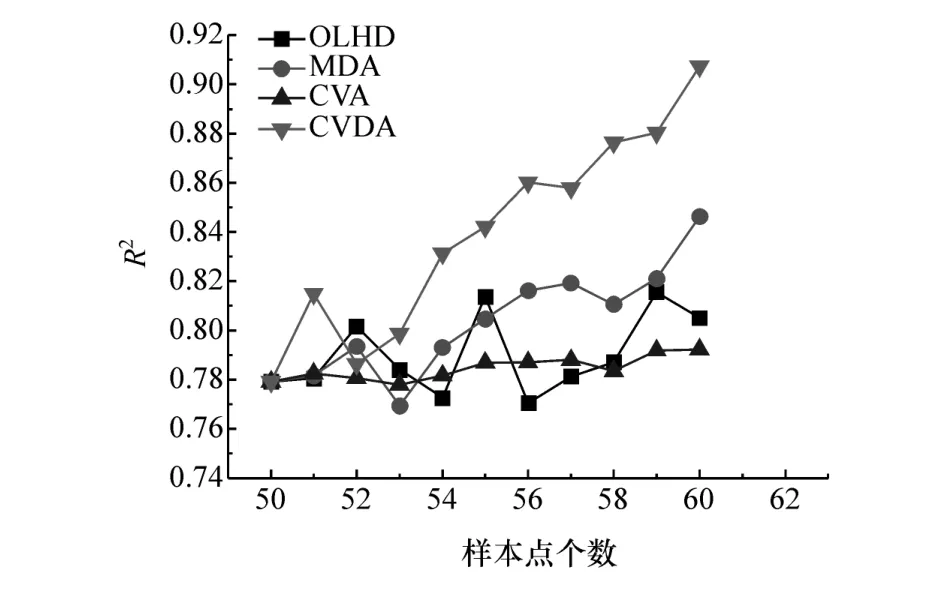
图15 扭转模态近似模型精度增长对比

由图14和图15可知，弯曲模态和扭转模态工况中，在初始样本点的基础上，分别进行12次和10次CVDA采样近似模型精度即可达到0.9以上。R2值均为0.907，与初始近似模型相比分别提升了17.51%和16.45%，最终样本点个数为62和60，比在相同数量样本点个数下预测精度最高的MDA法分别高出6.90%和7.21%。

4.2 多学科优化数学模型的定义

本次优化旨在保持车架原有性能（弯扭刚度和1阶弯扭模态）不降低的情况下，获得车架质量最轻时的壁厚匹配，即

min：MASS

s.t.：BENDstiffness＞9500 N／mm

TORSIONstiffness＞300000 N·m／rad

BENDmodal＞75 Hz

TORSIONmodal＞41 Hz

T1～T12＝｛1.0，1.1，1.2，…，4.8，4.9，5.0｝

式中：BENDstiffness为弯曲刚度；TORSIONstiffness为扭转刚度；BENDmodal为1阶弯曲模态频率；TORSIONmodal为1阶扭转模态频率。

4.3 优化结果分析

采用退火算法，经过3 671次全局迭代，获得满足约束条件下的全局最优解，优化结果如表3所示。

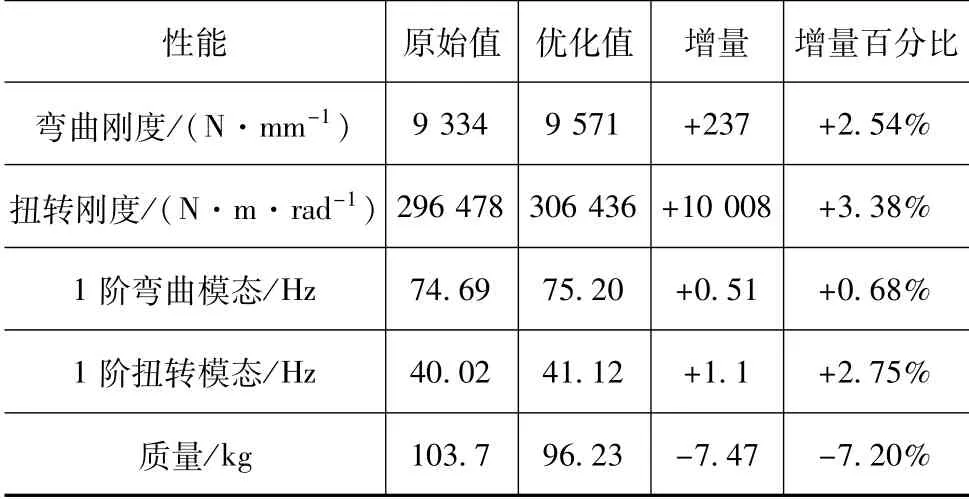
表3 全铝车架优化前后性能对比

由表3可知，弯曲刚度提升2.54%，扭转刚度提升3.38%，1阶弯曲模态频率提升0.68%，1阶扭转模态频率提升2.75%，质量减轻7.47 kg，减重率为7.20%，优化效果明显。

优化后的壁厚如表4所示。

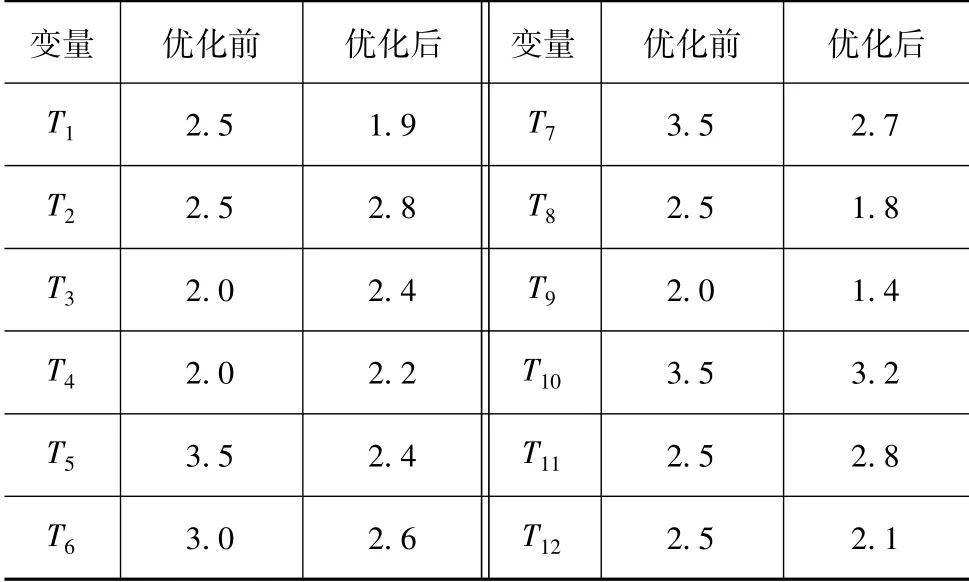
表4 壁厚优化结果 mm

5 结论

（1）通过数值算例对比OLHD法、MDA法、CVA法和CVDA法等4种采样方法对近似模型精度的影响，得出采用CVDA法采样可以准确定位低精度区域，在同样采取21个样本点下，预测精度较OLHD法、MDA法、CVA法分别高出11.1%，11.1%和30.3%。

（2）运用CVDA序贯采样法分别建立弯扭刚度、弯扭模态工况的近似模型，弯扭刚度分别采取32和31个样本点即可建立精度高达0.98的近似模型，弯扭模态分别采取62和60个样本点即可建立精度高达0.9的近似模型，大大提高了建模效率。

（3）全铝合金车架经过多学科优化，在弯曲刚度增加2.54%，扭转刚度增加3.38%，1阶弯曲模态频率增加0.68%，1阶扭转模态频率增加2.75%的情况下，质量减轻7.47 kg，减重率为7.20%，轻量化效果明显，为后续设计提供指导。