电动汽车充电站选址优化建模

杨 卫, 王 艳

(西安欧亚学院 金融学院, 陕西 西安 710065)

0 引 言

随着中国经济的飞速发展，汽车已成为平常家庭的代步工具，普及率迅速提升。汽车的使用给人们的生活带来了便利，但同时汽车排放的尾气也成为城市大气污染的主要来源。随着社会对环境污染、能源紧缺等问题的重视，各国政府积极采取各种措施，减少汽车尾气的排放，以减少对大气的污染。大力推广电动汽车，并让其逐渐替代燃油汽车，成为许多国家的共同选择。目前，电动汽车在污染物排放、能源消耗等方面都明显优于传统燃油汽车，但是由于充电设施及设备的发展还不完善，充电站布局不合理，严重制约了电动汽车的普及和发展。因此，研究电动汽车充电站规划选址问题，对于电动汽车的发展具有重要的意义。

国内外已经有很多学者从不同方面，针对电动汽车充电站选址的问题进行了研究。唐现刚等[1]基于计算几何方法，在考虑充电站运行成本、建设成本的情况下，建立了充电站选址的规划模型；加鹤萍等[2]建立了以交通流量为约束，充电站收益最大化为目标的电动汽车充电站选址模型；陈婷等[3]基于模拟退火算法，在考虑投资和运行成本的情况下，建立了充电站优化布局的模型；孟子杰[4]在考虑投资成本、年收入、运行费用的情况下建立了电动汽车充电站选址的优化模型；黄振森等[5]在考虑充电站建设总成本的情况下，建立了充电站选址的整数规划模型;刘志鹏等[6]在考虑充电站建设、运行等总成本及电网损失费用的情况下，建立了电动汽车充电站选址的优化模型； 王辉等[7]基于配电损耗和节点电压偏移最小、交通流量最大，建立了电动汽车充电站选址规划的数学模型。从以上文献中发现，学者在研究电动汽车充电站选址或规划布局等问题时，基本都是从成本、费用的角度考虑的，较少从使用者的角度考虑充电距离的问题。目前电动汽车得到各国政府的大力推广，许多地方给电动汽车使用者及充电站建设及运营者搞个补贴，但电动汽车在使用过程中，被抱怨最多的问题就是充电不方便，充电站距离远等，故文中将电动汽车用户的充电距离最小作为目标，以提高用户的使用满意度及便捷性，达到提高电动汽车普及速度的目的。

1 充电站规划选址模型

建立模型前，在考虑电动汽车使用者(用户)充电距离的情况下，先作出如下假设，候选选址点都符合充电站的建设要求，并充分考虑了需求分布。

1.1 符号说明

zij只能取0或1，当其值为1时，表示需求点j的用户会选择去候选选址点i充电;当其值为0时，则相反。Ri也能取0或1，当其值为1时，表示候选选址点i最终被选中建设充电站;当其值为0时，则表示没有被选中。

1.2 目标函数与约束条件

目标函数所有需求点的充电需求用户到充电站的充电距离之和最小

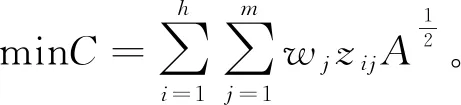
(1)

式中：A=[(ui-xj)2+(vi-yj)2]。

约束(1}表示一个需求点的用户最终只会选择到一个充电站充电

(2)

约束(2)是充电站建设数量的限制

(3)

约束(3)是充电站可充电动车的最大数量的限制

(4)

约束(4)是充电站充电收入要高于成本的限制

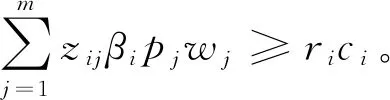
(5)

约束(5)～(8)是充电站选址及需求点的区域限制条件:

xmin≤xj≤xmax,

(6)

ymin≤yj≤ymax,

(7)

xmin≤ui≤xmax,

(8)

ymin≤vi≤ymax。

(9)

0-1决策变量为:

zij∈(0,1),

(10)

ri∈(0,1)。

(11)

2 算例分析

2.1 算例描述

在100 km×100 km平面内随机产生10个候选充电站和50个充电需求点,分布如图1所示。

考虑目前电动汽车充电的费用基本在2元/(kW·h)上下，故随机产生10个以2为中线的数，单位费用分别为2.0,2.2,2.1,2.4,1.8,2.1,1.9,2.4,2.0,1.9。作为每个候选充电站的单位充电费用(元/(kW·h))。由于每个需求点的需求数(单位：辆)和每辆电动汽车到充电站的充电量(kW·h)波动及随机性都比较大，故以均匀分布的形式随机产生。具体参数见表1。

假设每个充电站可充电动汽车的最大值均为600辆，候选充电站的成本分别为450,660,630,540,690,540,580,600,570,480万元。假设该区域要建设的充电站数量为5座。

2.2 算例结果及分析

运用Matlab软件求解得到了最优的结果，分别是选择在哪些候选站点建设充电站，以及各需求点基于最短距离最终会选择到哪个建成的充电站充电。

模型结果见表2。

图1 候选充电站及需求点分布结果图

表1 充电需求点的需求数及充电量

续表1

表2 模型结果

进一步对建设充电站数量与目标值之间的关系进行分析,如图2所示。

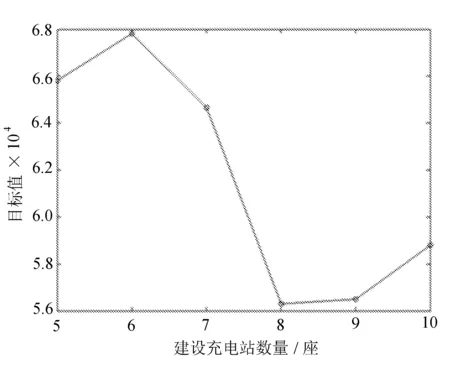
图2 建设充电站数量与目标值关系图

由图中可见，充电站数量并不是越多越好，在本算例的情况下，建设充电站数量为8座时，目标值最低。

3 结 语

研究了基于用户充电距离的电动汽车充电站选址问题，建立以所有需求点的需求用户到充电站的充电距离之和最小为目标的模型。模型根据实际需要，在保证充电站数量、充电站运行成本等情况下，得到应该在哪些候选站点建设充电站，以及各需求点最终会选择到哪个建成的充电站充电的最优结果。