工业经济增长的区域关联分析
戴嘉轩, 张海燕
(长春工业大学 数学与统计学院, 吉林 长春 130012)
0 引 言
在世界经济的大背景下,各国间的贸易往来正处于互相合作发展的大浪潮中,无论是国家间的协调合作还是国内各区域的繁荣发展,对经济发展的总效用来说都是有益的,而不同地区之间的经济发展既有差异性,又具有相关性。由于工业可以和其他方方面面的行业协调发展,促进经济健康有序的发展,因此一个地区的经济发展程度主要是由工业化程度这个指标来衡量。而吉林省作为东北老工业发源地,是工业发展的源头,因此,以吉林省工业经济增长为基础,研究各地区工业经济协调发展以及自身的发展轨迹,对如何促进工业经济全面繁荣,经济建设持续发展,人民生活水平提高都提供了重要的依据。吉林省是东北老工业发源地,具有人口少、地多、水多的地域特色,其重工业发达且发展速度迅猛,为国内工业生产总值产能的增加提供了一定基础。
改革开放以来,国内的工业结构问题一直是工业经济发展的主要条件之一,通过分析研究区域间的工业经济发展问题是解决经济增长缓慢原因的关键。在世界经济日益飞速发展的同时,我们可以通过借鉴国外丰富的经济学理论知识,将国内的经济发展现状结合起来进行综合性分析。吉林省作为老工业基地长期以重工业的发展为基础,具有典型的工业经济增长条件,用来解释区域经济与工业发展之间的关联性关系。从吉林省经济的工业化发展现状来看,发展水平较高的地区以长春市、延边自治州为代表,这些地区的城镇基础设施较好,城镇化水平较高,利于吉林省工业经济的发展。吉林省各地区之所以工业化发展水平不统一,是因为很多周边地区的城镇化建设步伐不一致导致的,对于一些生产能力低下、技术水平落后、资源整合能力不足的地区应给予适当的人才引进,对地区所固有的资源条件进行充分利用与吸收,同时进行厂区联建来加强各区域间的协调发展,配合工业与信息的产业融合,促进工业经济的发展。
1 吉林省各地区工业经济发展关联性分析
1.1 VAR模型建立
Sims[1-2]在1980年提出了向量自回归(Vector Auto Regression, VAR)模型,通常情况下,在经济学中应用回归分析模型一般要以经济学理论作为基础,利用生成的模型对经济主体进行行为描述,然后对模型的外生变量和内生变量进行分析。VAR(Vector Auto-regression Mode)矢量自回归模型的研究建立已经由最初的二维拓展到多维度[3],因为经济以及金融方面的时间序列分析经常涉及以上几个变量,所以通过VAR的研究建模,在实际的经济问题中得到了极为广泛地应用。
VAR(p)模型的数学表达式为
Yt=A0+A1Yt-1+…+ApYt-p+εt,
(1)
随着滞后期p足够大,模型的动态特征也能够被完整的展现出来,但随着p越来越大,导致模型的参数也越来越多,因此,需要寻找一种平衡态,一般利用AIC和SC法来确定p值。
1.2 VAR模型滞后期(p)的确定
由于VAR的滞后期(p)主要依赖于变量平稳性的影响。因此,首先需要对变量平稳性进行检验。Dickey等[4]提出DF统计量来检验变量的平稳性。由于模型中的残差项为白噪声,会有显著的自相关,因此可以在原式加入被解释变量的滞后项来消除自相关,这就得到了ADF(Augmented Dickey-Fuller)检验,具体模型如下:

(2)
如果原始数据没有拒绝原假设, 那么继续对数据进行标准化处理,之后将差分后的序列再次进行ADF检验,直到确定变量平稳拒绝原假设的前提下来建立VAR模型。在检验了变量平稳性之后,可以使用AIC和SC检验的方法来确定滞后期的检验。
AIC检验定义
SC检验定义[5]
滞后期的值根据AIC和SIC检验的值来确定。首先根据吉林省工业总产值(9个地区)数据进行对数差分之后建立模型1进行向量自回归,得到模型AR根图如图1所示。
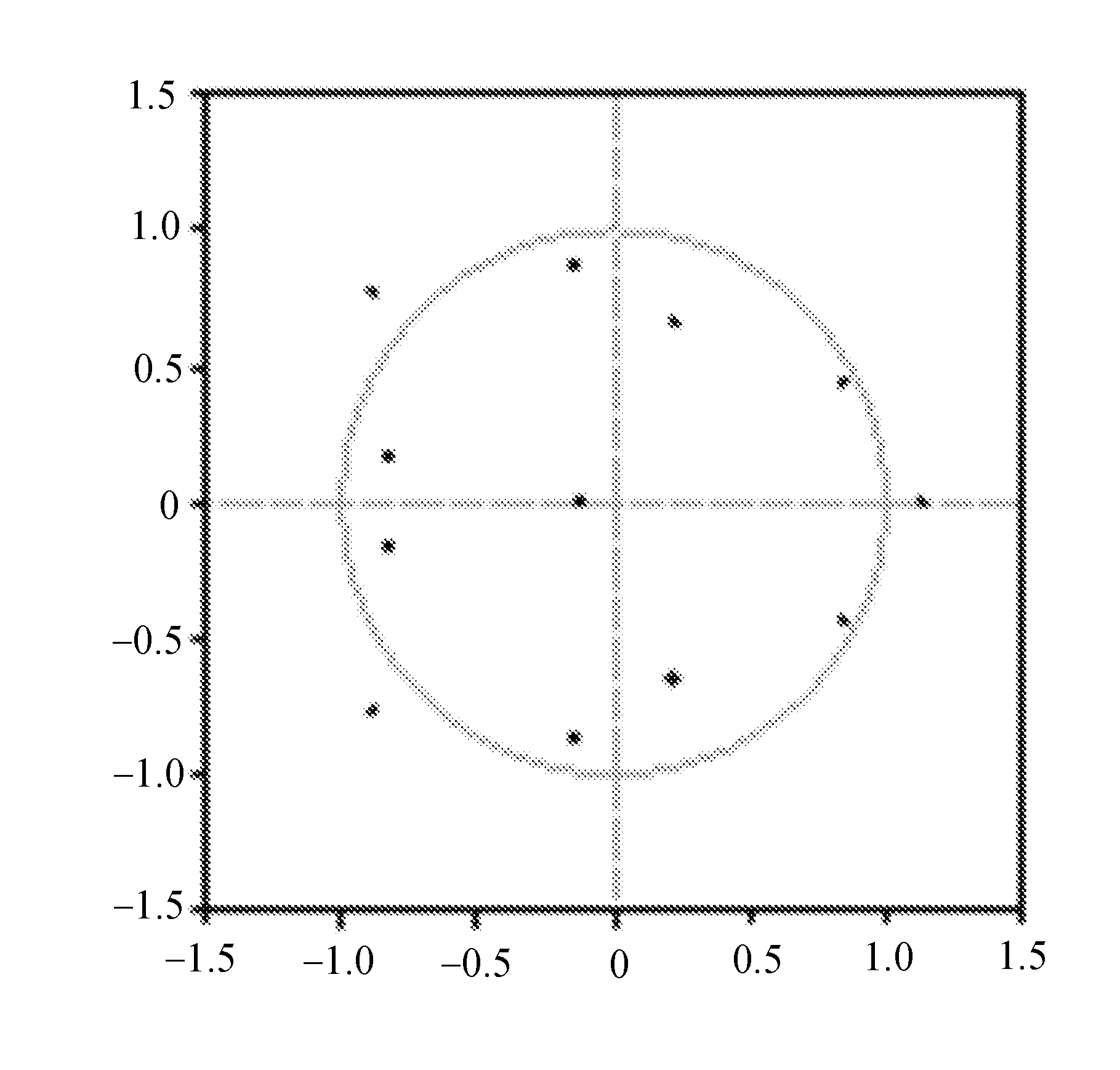
图1 模型1中的AR根图
图中可以发现有部分单位不在单位圆内,所以不满足稳定性条件,后续将不再通过脉冲响应函数和方差分解对其进行分析。
根据吉林省每一个地区的工业总产值以及GDP为两对数据进行对数差分之后建立VAR模型,在建立好模型之后,根据AIC和SC信息准则要求越小越好,回归计算结果如图2所示。
图2 模型2的回归统计结果
VAR模型的检验结果上一部分的每一列代表VAR模型中相对应方程的标准的OLS回归统计量,包括F统计量、AIC准则和SC准则等。根据AIC信息准则和SC准则取值最小的原则确定VAR模型为第2阶滞后变量,模型2的AR根图如图3所示。

图3 模型2的AR根图
从图3可以看出,模型2的AR根均小于1,即在单位圆内,则模型2通过平稳性检验,工业总产值与生产总值GDP之间存在长期稳定关系。
3.3.3 根据医院消毒供应中心技术操作规范中对灭菌物品的有效期要求D,棉布在储存环境达标的情况下,保存期限为14 d(如无法确定达标,则保存期限为7 d)。但是由于每天手术种类和数量的不确定性,尤其是节假日时,常常导致过期包的出现。另外,棉布的吸水力强,较易受潮,容易产生灭菌湿包以及灭菌后容易被再次污染,而导致无菌器械包失效[5]。这些包需要重新包装、消毒,增加了相关人员的工作量及科室成本。
2 脉冲响应函数和方差分解
脉冲响应函数主要用来评估随机扰动项的标准差对于内生变量现在和未来值的影响,并且这种影响会通过VAR模型影响到所有的变量。Sims利用Wald分解定量转换成移动平均的方式来更加直接评估变量间的关系[6],具体过程如下:
(1-β1L-β2L2-…-βmLm)Yt=α+εt,
Yt=(1-β1L-β2L2-…-βmLm)-1α+
(1-β1L-β2L2-…-βmLm)-1εt,

(3)
式中每一个变量都可以表示内生变量的当期和滞后期,互相受到随机冲击波的响应时,这些线性组合由于这些随机冲击项可能会存在当期的相关性,因此使用Choleski分解法来消除这种相关性。
使用一个下三角矩阵对式(3)进行变形

(4)
从式(4)中可以看出,每个变量都可以由各期的随机冲击项表示,由此得到了脉冲响应函数。在分析VAR模型时,不能仅仅分析一个变量的变化对另一个变量的影响情况,而是分析当一个误差项发生变化,模型受到某种冲击时对系统的动态影响。在对脉冲响应函数进行分析时,可以采用 Chol-esky 分解法,即用小样本的自由度修正来构建残差协方差矩阵的 Cholesky 因子的逆正交化矩阵。如果脉冲响应函数均趋于0,则说明构建的VAR模型是稳定的。
脉冲响应函数(Impulse Response Function)描述的是一个时间序列变量在受到一个单位的随机扰动因素的冲击后的动态变化路径,是对误差冲击的反应。它能够直接描述出各个变量的动态交互作用以及效应。Granger因果检验可以找出哪种变量出现变化对其他变量未来值存在统计意义上的影响,但这种检验的缺点是无法确定这些关系在长时间内起多大的影响,而脉冲响应能找到这些影响。
VAR模型脉冲响应函数图如图4所示。

图4 VAR模型脉冲响应函数图
由图4分析可知,从第1期开始,当工业总产值受到一个正冲击后立即做出响应,这种响应达到了最大值,工业总产值自身的这种扰动冲击对工业总产值影响的持续时间比较长,直到10期后,工业总产值的变化才趋于0。工业总产值响应趋近于0,是因为所估计的VAR模型是平稳的。而工业总产值对于来自生产总值GDP的扰动并没有立即做出响应,工业总产值在第1期的响应为0,在之后的第2~4期工业总产值对生产总值GDP所做出的响应达到最大(约为0.05左右),但同时生产总值GDP所做出的响应也是负向的,直到后来的第10期,响应逐渐降低趋近于0。当生产总值GDP受到一个正冲击后就立即做出了响应,当第1期到第2期,生产总值GDP所做出的响应呈上升趋势。从第2期以后,生产总值GDP所做出的响应出现下跌且是负向的,最终响应逐渐降低趋近于0。生产总值GDP受到一个正冲击后就立即做出了响应,当从第1期到第2期做出的响应呈下降趋势,也是有负向的效应,从第2期以后脉冲响应趋近于0。综上所述,如果工业总产值受到外部的干扰或冲击之后,会具有显著的持续性效应,对吉林省生产总值GDP具有正向影响,对工业经济增长起到推动作用。
方差分解方法是通过分析每一个结构冲击对内生变量变化的贡献度,以方差来度量不同结构的重要性。利用方差分解可以分析VAR模型中变量产生影响对自身变量或其他变量贡献率的变化,即一个系统中给定的变量出现变化时,对其他变量的影响是正向还是负向的,同时在系统内,这个变量变化会存在多长时间以及多大程度的影响。
方差分解结果如图5所示。

图5 方差分解结果图
根据图5可以得到分析结果,随着预测期的连续推移,经济增长方差中有工业总产值自身扰动引起的百分比缓慢下降,而生产总值GDP扰动所引起的百分比缓慢增加,在预测的第10期保持稳定。工业总产值对自身的贡献率是逐渐下降的,对生产总值GDP的贡献率是逐渐上升的;生产总值GDP对工业总产值的贡献率是逐渐上升的,对自身的贡献率是逐渐下降的。
3 结 语
根据上述数据可以看出,VAR模型可以反映出现实中经济发展的趋势,吉林省工业经济增长对其生产总值GDP在短期和长期均具有显著正向和反向推动作用。同时,工业生产总值和生产总值GDP的增加也会对自身产生滞后影响。工业经济发展是衡量一个地区经济发展好坏的主要因素,作为东北老工业基地的吉林省,曾经为中国的工业发展做出了巨大贡献,是我国经济建设起步时重要的工业支柱[7]。在一定的时间范围内,工业经济的发展一般会存在统计学上的稳定性,吉林省各地区的工业发展也有这样的特点,长春市是吉林省的省会,与各个地区的发展都存在千丝万缕的联系,因此,长春市与各地区的因果关系和解释能力存在稳定的关系[8]。虽然在工业经济发展过程中有着各种各样的好坏因素,但吉林省内的工业经济发展还是有着比较稳定的上升趋势,工业生产总值有比较好的水平,地区之间工业经济的发展相互关联,互为促进融合。

