基于双焦点设计的平面波束扫描透镜天线研究

(中国电子科技集团公司 第五十四研究所，石家庄 050081)

0 引言

随着卫星通信、导航、雷达抗干扰等技术的快速发展，对多波束扫描天线提出了更高的要求。透镜天线的低成本、宽频带、宽角范围内多波束扫描且馈电网络简单等特性，倍受天线设计人员的青睐[1-2]。在光学领域和聚焦领域，根据费马定理，透镜能使焦点处的球面波转变为等相位平面波前，透镜天线就是由此制作而成[3-5]。

透镜天线的形式很多，透镜可以由金属[6]或非金属介质构成，也可以是由单元组成的平面周期结构。传统介质透镜天线的研究较早，实现波束扫描的方法多且成熟，如分区透镜[7]、龙伯透镜[8]、双焦点透镜[9-10]等。曲面的阵列天线的波束控制也趋于成熟[11]。而一般平面透镜实现波束扫描都是基于单焦点透镜的偏焦原理，直接使用设计出来的单焦点透镜，通过馈源偏焦来实现扫描[5,12]，但馈源偏焦会聚焦变差并产生能量漏失，最终导致增益下降，尤其在扫描角度较大时增益下降更快。因此在较大角度的扫描范围内，提升透镜天线的最低增益具有重要的研究意义。

1 平面透镜天线原理

1.1 广义折射率理论

广义折射率理论[13]基本原理如图1所示。电磁波从A传播到B，穿过两种介质，考虑一束平面波以θi角入射到界面上，定义入射界面与界面相交的线为x轴，并假设从A到B有两种路径ADB和AEB，它们都与实际光路无线接近，界面上的相位突变为Φ(x)。在两种介质交界的界面利用费马定律，那么这两条路线的相位差应该近似为零。则得到广义折射率：

图1 广义折射率原理图

(1)

其中:Φ和Φ+dΦ分别为两个光路通过界面时的相位突变，dx是界面上两点的距离，ni和nt是两种介质的折射率，k0为电磁波在真空中的波数。

由式(1)可知，通过调节两种媒质界面横向分布的不连续相位，可以实现控制电磁波的折射角度，表现在远场上则可以做到任意控制波束的辐射方向。

1.2 平面透镜天线聚焦原理

透镜是聚焦器件，能将焦点馈源发射的球面波转变为平面波前出射，或者将入射的平面波聚焦，在光学领域和聚焦领域运用广泛。根据不同的运用功能，适当地改变透镜的几何外形和材料的介电常数，透镜天线可以有多种应用。

平面透镜是由单元阵列而成的，其原理就是在单元中间加入特定的结构，控制该结构可以使工作频率的电磁波透过时能够造成不同的相位延时，从而控制输出所需要的相位波前[2]。根据广义折射率理论，即可实现控制电磁波的折射角度，表现在远场上则可以做到任意控制波束的辐射方向。根据阵列设计理论和几何光学理论，合理地调节透镜单元的补偿值，从而使馈源发射出的球面波转换为平面波，最终在远场所设计方向获得所需波束，如图2所示。所以平面透镜天线的研究包括三个部分：

1)馈源。馈源的波束宽度决定了平面透镜天线的焦径比，波束形状及相位中心决定了平面透镜的相位补偿分布，而且馈源的增益对透镜天线的增益也有重要影响。另外馈源的设计还需要充分考虑极化方式、尺寸、稳定性等实际需求，因此对于不同平面透镜天线，需要设计符合相应设计要求的馈源。

2)单元。单元是组成平面透镜的基础，它的透射特性直接影响着平面透镜的透射性能。所以根据平面透镜天线的设计需求，需要考虑在频带内相移范围和透射幅度，以及在半照射角范围内斜入射时的相移和透射幅度的稳定性等；

3)相位补偿分布。相位补偿分布指导透镜上单元的布局，决定透镜天线增益和波束指向。

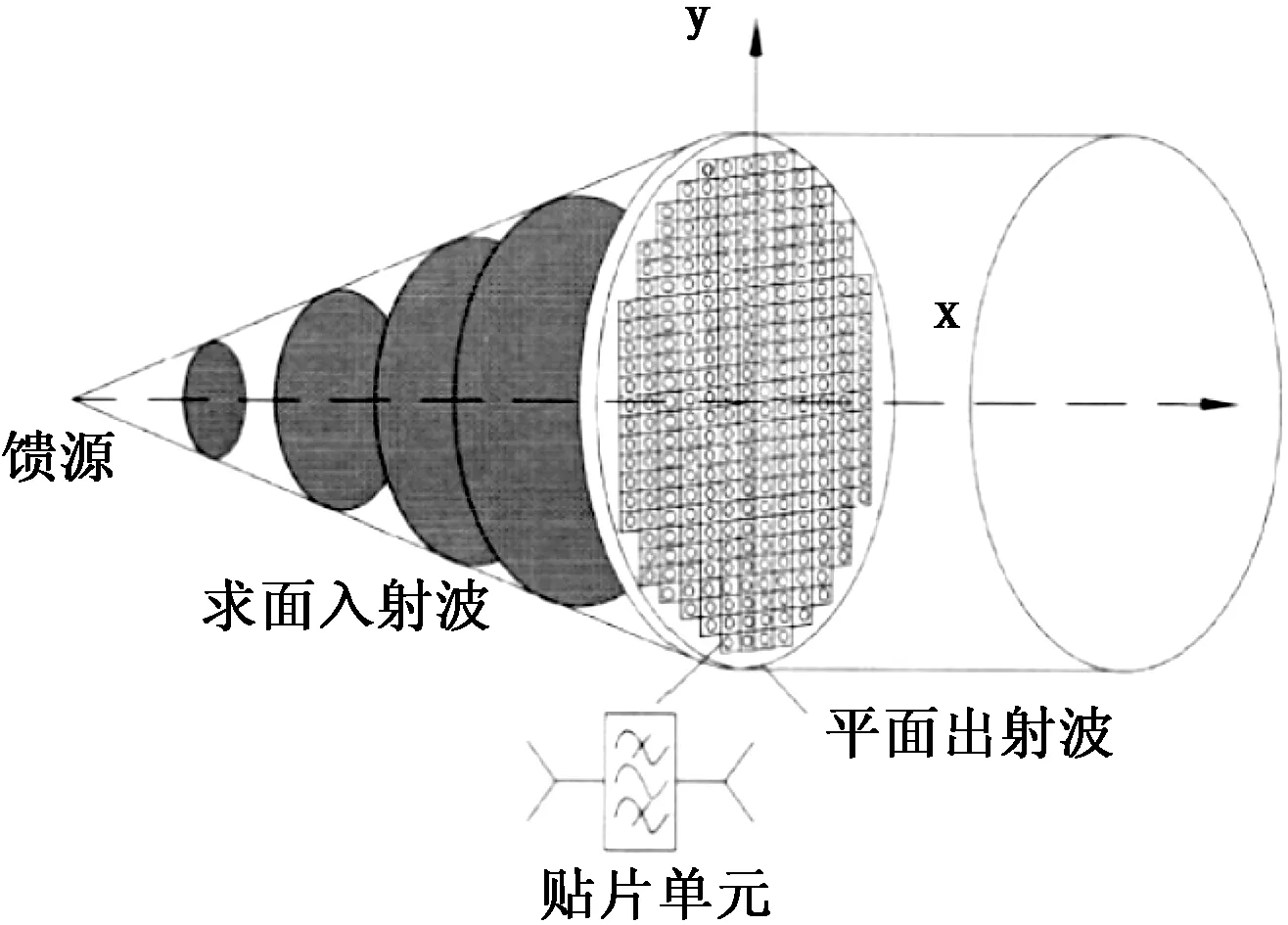
图2 平面透镜天线

1.3 平面透镜天线扫描原理

一般平面透镜实现波束扫描都是基于单焦点透镜的偏焦原理，直接使用设计出来的单焦点透镜，通过馈源偏焦来实现扫描。当馈源平行于透镜平面偏离焦点位置时，平面透镜天线产生的波束将发生扫描。馈源偏焦会使照射到平面透镜的电磁场产生相位变化，并且使馈源的波束宽度与透镜的覆盖范围失配，产生能量漏失，最终会导致平面透镜天线的增益和口径效率下降、副瓣上升以及方向图波束指向变差[2]。

为了改善平面透镜天线的扫描效果，借鉴了反射阵列天线[14-15]以及双焦点介质透镜天线[9-10]的双焦点技术，结合透镜单元的透射相位和幅度控制。采用了两种双焦点的相位补偿分布，从而使透镜的焦弧面更接近平面，改进了透镜天线的扫描角度和扫描效果，为多波束的实现提供了可行性。

2 平面透镜天线设计方法

2.1 单焦点平面透镜天线

由于研究使用的馈源和单元相同，平面透镜天线设计的重点在于相位补偿分布。

根据费马原理，用单元分区的方法来计算每个单元应该补偿的相位，使出射平面上的波束等光程，即可出射平面波。通过计算每个透镜单元到馈源之间的距离，算出它们之间的相位差，然后根据需要补偿的相位差，来调整单元的参数，使球面波前通过平面透射天线变成等相位平面波前，如图2所示。

因此单焦点平面透镜天线的相位补偿分布为：

(2)

其中:k0为电磁波在自由空间的波数，F为透镜天线的焦距，φ0为初始相位，取决于单元的透射性能。当单元的斜入射和直入射透射系数相差不大时，则透镜天线的理论透射误差为：

(3)

其中:S21(m,n)为单元(m,n)的透射幅度，以透射误差最小为目标，筛选即可得到最优的初始相位。

2.2 一维双焦点平面透镜天线

一维双焦点平面透镜天线应能在含焦点的平行与透镜的一条线上进行扫描，文献[14]采用了两个对称的偏心单焦点相位补偿分布做平均，作为在一维双焦点反射阵中的相位补偿分布。本文将其应用到一维双焦点透镜中。

由于偏心单焦点透镜(如图3所示)的相位补偿分布为：

(4)

其中:

a=Ftanθ

(5)

对称可得：

(6)

其中:F为焦距，θ为馈源指向与轴线的夹角，即馈源偏移角度。

则一维双焦点透镜的相位补偿分布为：

(7)

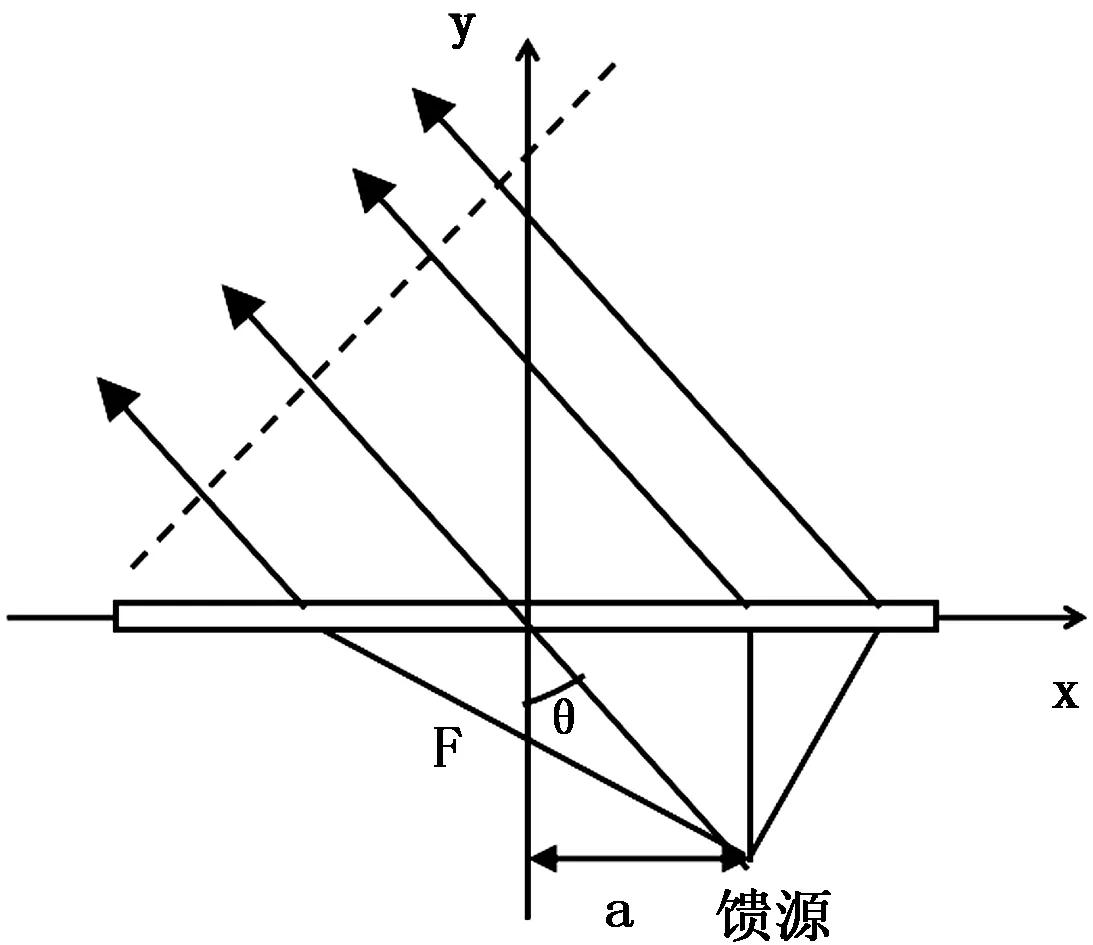
图3 偏心单焦点透镜天线

2.3 二维双焦点平面透镜天线

双焦点平面透镜的研究关键在于透镜上的相位补偿应该如何分布。由于实际透镜的仿真计算较慢，不利于优化设计，而且单元或多或少都有缺陷。针对一种相位补偿分布，基于阵列合成理论，可以模拟出其理想的透镜天线，并利用Matlab平台计算理想透镜天线的方向图和方向性系数，从而可以判断该分布的合理性。具体计算方法如下：

二维阵列透镜中，馈源经过单元(m,n)后的出射相位：

(8)

其中:k0为电磁波在真空中的波数，lmn为馈源到单元(m,n)的距离，φmn为该单元的补偿相位，d为单元间距。

如果假设馈源到透镜的电场是均匀的，则可以计算出经过透镜后的电场：

(9)

如果假设馈源是高斯馈源，且在照射角α0的边缘照射电平下降了10 dB，则经过透镜后的电场：

(10)

其中:

(11)

(cosα0)q=0.1

(12)

αmn为单元(m,n)与轴线的夹角。

从而计算出功率：

P=|E(θ,φ)|2

(13)

根据方向图定义计算出方向图：

(14)

取最大值即为方向性系数。

由于实际透镜单元会有反射损耗等因素，以及单元在透镜中并不完全符合周期性边界导致了相位补偿不会完美。这种方法计算的方向性系数往往偏高，但仍能用来判断相位补偿分布的合理性。

二维双焦点平面透镜天线应能在含焦点的一个平面上扫描。所以二维双焦点透镜的相位补偿分布是圆对称的，如图4所示，补偿相位只与单元到透镜中心的距离有关。所以设一维向量r1×q和与之对应的x1×q，其中r1×q的元素为到透镜中心的距离，x1×q为该距离下对应的补偿相位。为简化变量，r1×q的元素以单元的一半长度为间距均匀取值，默认x1为0。则整个透镜的补偿相位可以根据r1×q和x1×q的元素做插值取得。

图4 双焦点透镜的等相位补偿线

采用粒子群优化算法，以在馈源偏移轴向θ角度时的方向性系数取得最大值为目标，优化向量x1×q，即可得到二维双焦点透镜上的相位补偿分布。

3 平面透镜天线仿真

3.1 馈源

本文采用的馈源为圆口径波纹喇叭馈源，如图5所示。该馈源的频带为11～15 GHz，选定的工作于Ku频带(12.25～14.5 GHz)。在中心频率13.375 GHz处E面和H面方向图如图6所示，选取透镜天线的照射角为45°，即透镜天线的焦径比为0.5，透镜边缘照射电平为11.89 dB。在照射角内，馈源的E面和H面等化良好。

当需要扫描角度θ时，馈源平行于透镜偏移Ftanθ的距离，F为焦距，且馈源始终指向透镜中心。

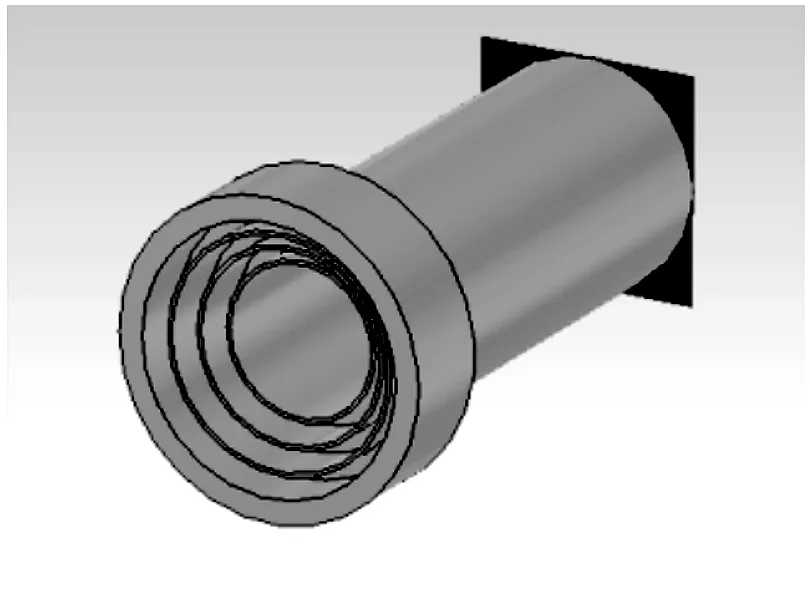
图5 喇叭馈源

图6 13.375 GHz处方向图

3.2 单元

平面透镜的单元有很多种，根据工作原理不同可分为：频率选择单元[5,12]、接收/发射单元[16]、惠更斯单元[3]、超材料单元[5,17-18]等。根据透镜天线原理，理想的透镜单元需要满足以下条件：单元应当在保持高透射的同时，能够实现360°相位调节；单元在斜入射时透射性能不变；若要透镜天线实现宽频带，则单元一定是宽频带的。

本文中选取的单元为文献[18]中的介质打孔单元，该单元原理为改变在介质中孔的大小，能够改变其等效介电常数，从而改变单元移相。为了进一步提高单元的透射性能，在单元前后各添加了打孔的介质作为匹配层。如图7所示，单元边长为6 mm，移相层介质厚度为13.35 mm，孔半径为r1，介电常数为10.2。匹配层介质厚度为3.36 mm，孔半径为r2，介电常数为3.19。移相层和匹配层的孔半径为线性关系：

r2=1.05r1-0.38

(15)

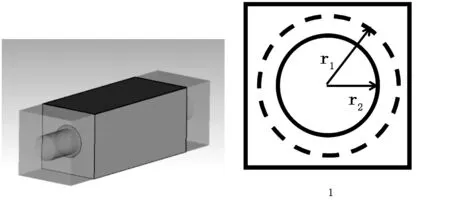
图7 介质打孔单元

通过改变移相层孔的半径r1，即可改变的单元的相移。周期边界条件下仿真得，该单元的透射系数如图8和图9所示。在频带(12.25～14.5 GHz)内，单元都可以实现360°相位调节，且单元透射幅度都高于-0.5 dB。在中心频率处斜入射时，透射幅度仍保持高于-0.5 dB，且透射相位与直入射时相比变化不大。单元的各项透射性能都很好，有利于研究透镜的相位补偿分布对扫描性能的影响。

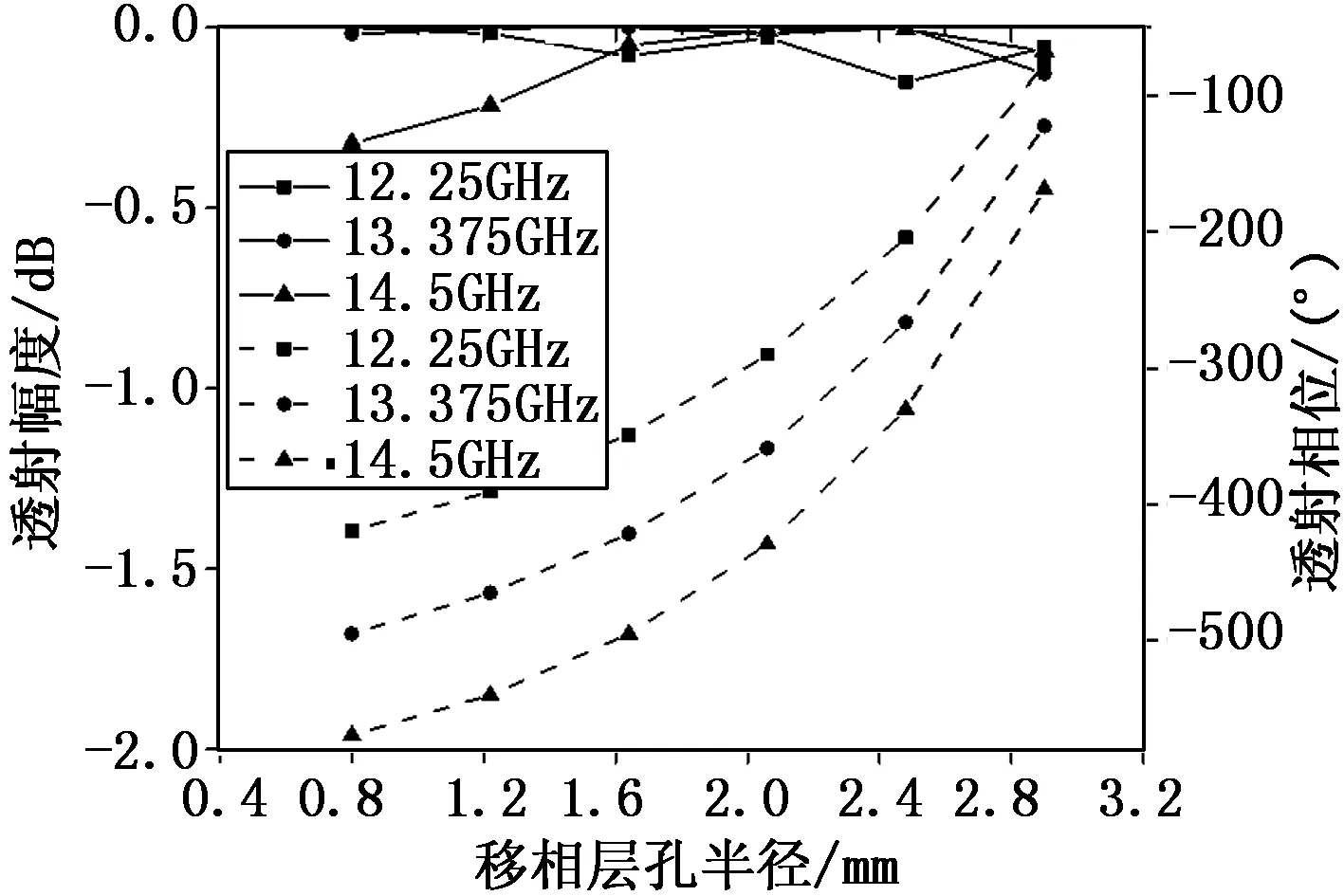
图8 垂直入射时透射性能

图9 中心频率处斜入射时透射性能

3.3 平面透镜天线的轴向辐射特性

仿真得三种透镜如图10所示。透镜的总厚度为20.07 mm，直径为192 mm，透镜天线的焦径比为0.5。

三个透镜天线在频带(12.25～14.5 GHz)内的增益和口径效率见表1，单焦点透镜天线在中心频率处增益为25.65 dB，口径效率为50.30%。在整个频带内，单焦点透镜天线的口径效率比较稳定，都在50%附近，也与单元宽带性能分析一致。

因为双焦点透镜天线要提升扫描性能，牺牲了馈源在焦点时的增益，所以双焦点透镜天线在馈源未偏移时的增益都比单焦点透镜天线低。两个双焦点透镜相比，二维双焦点透镜天线的增益和口径效率更高。

图10 三种透镜

表1 三种透镜的增益和口径效率

3.4 平面透镜天线的扫描性能

仿真在中心频率(13.375 GHz)处，扫描方向与主极化方向垂直时，馈源偏移0°～30°时扫描的增益见表2和图11。

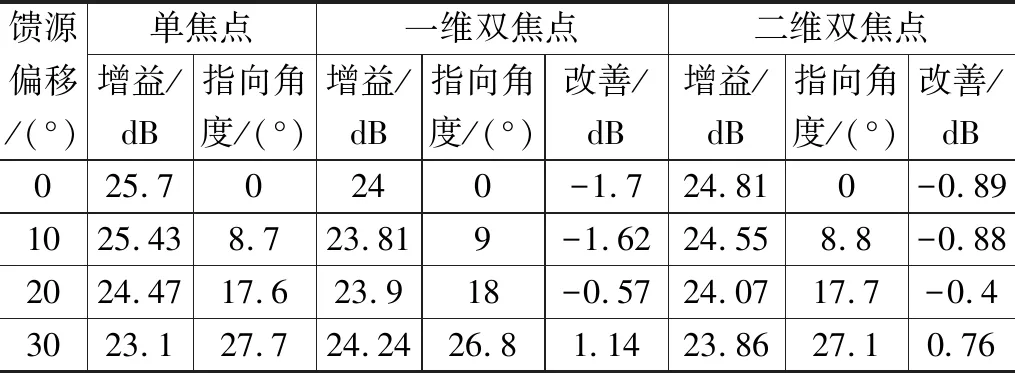
表2 仿真单双焦点透镜的增益

由表2可知，馈源偏移0°时，一维双焦点透镜天线和二维双焦点透镜天线相对单焦点透镜天线增益分别降低了1.7 dB和0.89 dB，但当馈源在偏移30°时即指向角度约27°时，增益分别提升了1.14 dB和0.76 dB，双焦点透镜天线的扫描损耗较小。平面透镜天线的实际波束指向角度比馈源的偏移角度小，而且对于三种不同的平面透镜馈源偏移角度相同时，天线实际指向角度只有很小的差距。所以在扫描范围0～27°内单焦点透镜天线最低增益为23.1 dB，一维双焦点透镜天线和二维双焦点透镜天线最低增益分别为23.81 dB和23.86 dB，分别提升了0.71 dB和0.76 dB，而最低口径效率分别提升了4.97%和5.35%。

如图11所示，可以直观地看出双焦点透镜的扫描损耗小，在扫描范围内的最低增益大，扫描性能相比单焦点透镜天线有所提升。证明了研究的双焦点透镜天线的扫描性能比单焦点透镜天线有了明显的提升。

图11 仿真单双焦点透镜的增益

两个双焦点平面透镜天线相比，二维双焦点透镜天线的扫描范围更广，扫描最低增益更高，具有更大优势。

三种透镜的扫描方向图如图12～14所示，单焦点透镜天线、一维双焦点透镜天线和二维双焦点透镜天线在扫描范围内的最大3 dB波束宽度分别为11.4°、11°和9.6°，可以看到二维双焦点透镜天线对扫描波束宽度的降低较为明显。

图12 单焦点透镜扫描方向图

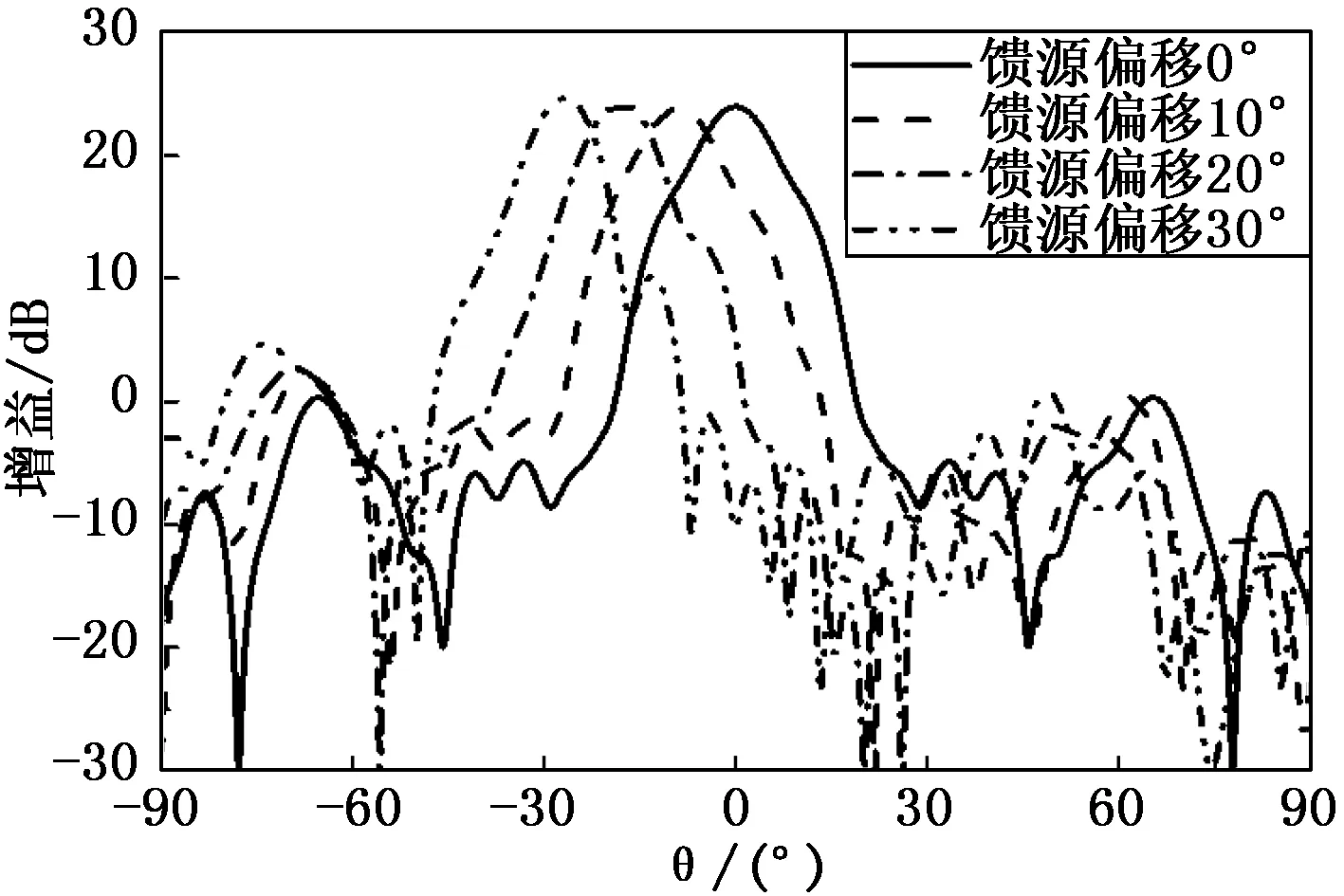
图13 一维双焦点透镜扫描方向图

图14 二维双焦点透镜扫描方向图

4 结束语

针对传统方法设计的波束扫描平面透镜天线在扫描过程中增益损失大、最低增益低的问题，提出了基于双焦点的透镜补偿相位分布。基于阵列合成理论，计算了理想透镜天线的辐射特性，也给平面透镜天线的补偿相位分布提供了一种评估方法通过仿真分析可知，双焦点透镜天线的设计方法是可行的，双焦点设计不仅提升了平面透镜天线扫描范围内的最低增益，而且降低了大角度扫描时的波束宽度，整体提升了平面透镜的扫描性能。其中二维双焦点透镜天线具有更广的扫描范围，更好的扫描性能。