基于数值仿真的离心风机叶片优化设计

陈加瑞，黄 昭，刘之雷，黄忠文

武汉工程大学机电工程学院，湖北 武汉 430205

离心风机是一种提供气体动力的流体机械，广泛应用于通风、排尘、冷却等工业生产过程中［1］。离心风机的主要零部件为叶轮、蜗壳、进气口、扩散器等［2］，其中叶轮是关键部件，离心风机的工作状况主要取决于叶轮的具体结构［3-4］。对离心风机的叶片进行优化设计可以有效地降低离心风机的能耗，这对于我国的可持续发展战略具有重要的实际意义［5-7］。

本文以9-26-10D型离心风机为具体研究对象，利用相关软件进行建模、网格划分以及计算，最后根据数值模拟的计算结果对离心风机的叶片进行优化设计。

1 离心风机内部流场研究

理论分析法、实验研究法和数值模拟法是研究离心风机内部流场的三种主要方法［8］。目前应用最为广泛的方法为数值模拟法，这种方法可以较为直观的观察到流体机械的内部流场［9］，实践表明通过数值模拟得到的计算结果精度高，而且计算时间短，研究成本低。所以，采用数值模拟法来研究离心风机的内部流场是一种较为可靠的方法。

1.1 流体力学的基本方程

1）在本文中假设离心风机的气体为理想可压缩气体，则质量守恒方程为：

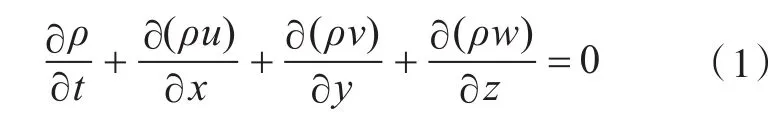
引入矢量符号div(a)=式（1）可写成：

式（1）中：ρ为流体密度，单位kg/m3；t为流体流动时间，单位 s；U为速度矢量；u、v、w为速度矢量U在x，y和z方向的分量。方程（2）也可作为可压缩气体的连续方程。

2）离心风机中的气体遵循动量守恒定律。动量守恒方程为：

式（3）～（5）中：p为作用在流体上的压力，单位：Pa；τxx，τxy，τxz为粘性应力在 x，y，z方向上的分量；Fx、Fy、Fz为体积力在x，y，z方向上的分量。

3）离心风机内部气体也要满足能量守恒定律。能量守恒方程为

式（6）中：cp为流体的定压比热容，单位为J/kg·K；T为流体的温度，单位为K；k为流体的导热系数，单位为W/（m·K）；ST为流体内部热源，也称为黏性耗散项。

1.2 湍流模型

标准k-ε模型是应用最为普遍、最有效的湍流模型［10］。该模型计算结果较为准确，而且计算收敛快。标准k-ε模型的运输方程为：

2 离心风机的数值模拟仿真

2.1 建立模型与网格划分

由于9-26-10D型离心风机采用的是二元叶片，故对风机回转截面进行建模。该离心风机原始模型中，叶片数目为16片，进口角度为38°，出口角度为126°，叶片圆弧段半径为125 mm，叶片厚度为3 mm，叶轮的转速为1 450 r/min。离心风机的模型及尺寸如图1所示。

图1 离心风机：（a）计算模型，（b）叶片相关尺寸图Fig.1 Centrifugal fan：（a）calculation model，（b）dimensions of blades

对离心风机进行网格划分：通过内部面将流场分为静止区域和流动区域两个部分，其中流动区域的流场较为复杂，因此只将这一区域的网格密度划分得更加细密，这样可以使得计算速度更快，并且计算精度不会受到影响［11-15］。

2.2 内部流场数值模拟

离心风机内部流场比较复杂，需要设定多重坐标系来模拟离心风机叶片的转动，叶轮流动区域采用旋转坐标系，蜗壳区域为静止网格，两区域之间的交界面设置为interface。

利用相关软件进行数值模拟的计算结果如图2所示。

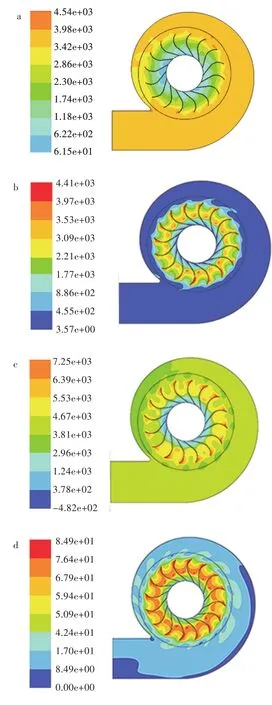
图2 离心风机：（a）静压分布云图，（b）动压分布云图，（c）全压分布云图，（d）速度矢量云图Fig.2 Centrifugal fan：（a）nephogram of static pressure，（b）nephogram of dynamic pressure，（c）nephogram of total pressure ，（d）nephogram of velocity vector

图2（a）为离心风机内部静压云图，静压是因流体在叶片前后产生压力差所致，其大小与出入口尺寸和叶片转速有关。在风机进口处静压为负值，然后沿径向逐渐增加，并且离叶轮区域越远静压越大，距离叶轮最远处的蜗壳区域静压增到最大。

图2（b）为离心风机内部动压分布云图，由于动压与流体速度的二次方成正比，因此流速的变化对动压有显著的影响。气体进入流道后，越靠叶轮外侧动压越高。气体进入蜗壳后，动压减小，动压在距离蜗壳最远处最低。

图2（c）为离心风机内部全压分布云图，全压为动压与静压的总和。全压的变化规律与静压、动压变化规律基本一致，也是沿着叶轮径向逐渐增加，在叶轮尾部全压最大，叶片工作处的全压比叶片背面处的压力大。

图2（d）为离心风机的速度分布云图，其分布规律和动压分布云图相似，从图2（d）中可以看出靠近叶轮尾部速度很大。气体以较高的流速流入蜗壳流道后，随着流道截面面积逐渐变大，气体速度开始变小，气体的动能转换成压力势能。

3 优化计算分析

在原始离心风机内部流场的分析基础上，改变叶片数量和叶片圆弧半径，然后继续进行数值模拟仿真计算，最后根据数值模拟获得的离心风机性能数值进行叶片的优化设计。

3.1 不同叶片数量的计算分析

以9-26-10D型离心风机为研究对象，将叶片数量分别更改为10片、12片、14片、16片、18片、20片、22片，保持叶片的其它参数不变。通过数值模拟计算得出的性能曲线图如图3所示。

图3（a）为离心风机在不同叶片数量下的流量—全压曲线图，由图3（a）可知：风机的全压会随着流量的增加而减小。另外，可以明显的看出当叶片从12片依次增加到18片时，风机的全压也增加了，增幅比较明显。当叶片从18片依次增加到22片时，风机的全压虽然也增加了，但是增幅并不显著。

图3（b）为离心风机在不同叶片数量下的流量—效率曲线图，从图3（b）可知：风机的效率随着流量的增加而呈现出先增大后减小的趋势，当叶片数量从12叶片依次增加到18叶片时，风机的效率增加得比较明显，当继续增加叶片数量时，风机的效率并没有加大幅度的提升。

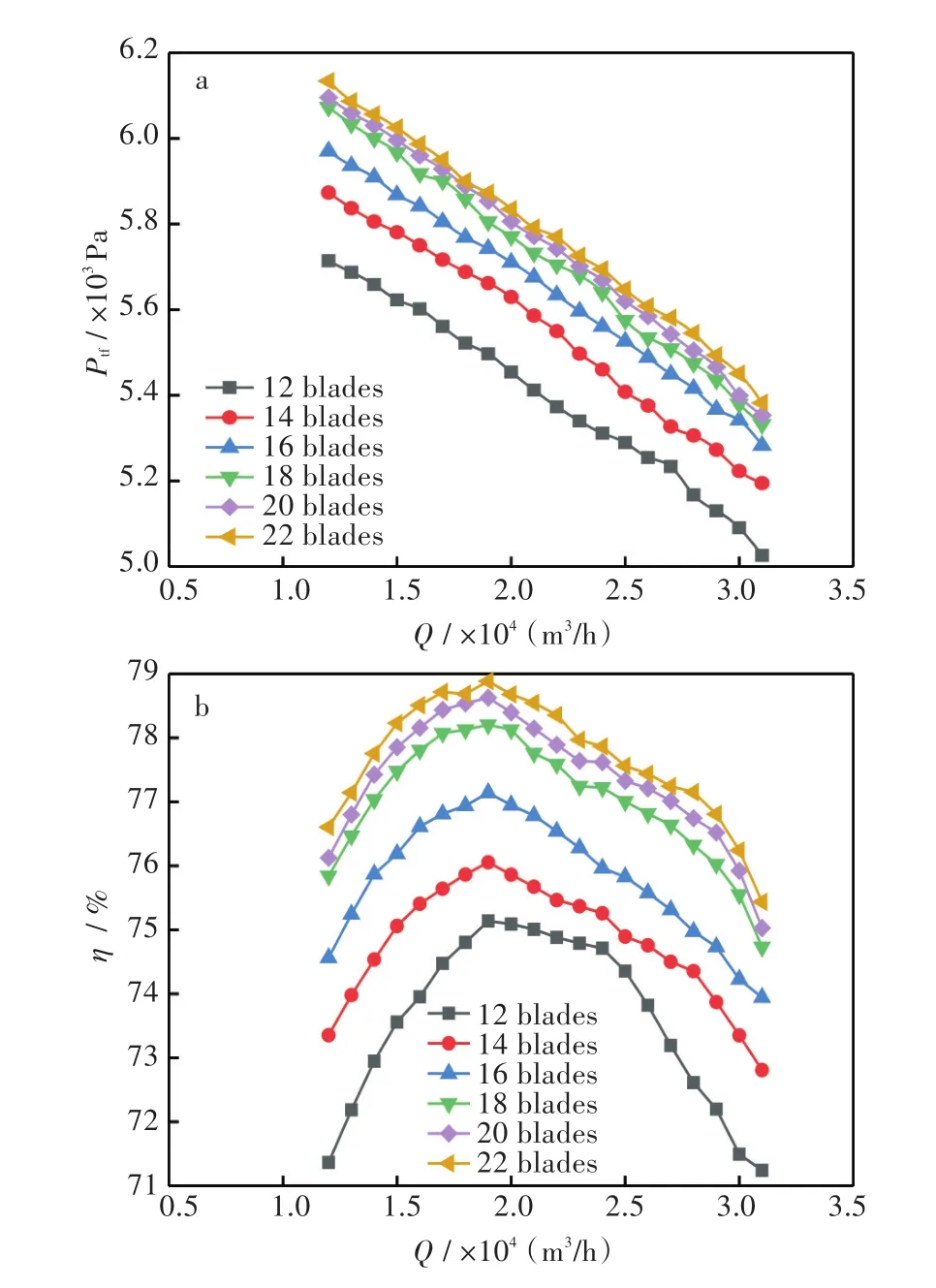
图3 离心风机性能曲线：（a）流量-全压性能曲线，（b）流量-效率性能曲线Fig.3 Curves of centrifugal fan performances：（a）flow-full pressure，（b）flow-efficiency

叶片数量越多，离心风机的摩擦损失就会越来越大，会对风机的性能造成较大的影响。综合考虑风机的效率和成本，最终选择的风机叶片数量优化模型为18叶片。

该型号离心风机的流量在19 000 m3/h附近时，效率较高。在流量为19 000 m3/h处，其主要性能参数如表1所示。

表1 不同叶片数量在风机流量为19 000 m3/h时的主要性能参数Tab.1 Performance parameters of different blades at flow rate of 19 000 m3/h

由表1可知：当叶片数量为18片时，风机全压为5 805.57 Pa，效率为77.98%；对于叶片数量为16片的原始模型，其风机全压为5 675.50 Pa，效率为76.23%。因此，与原始模型相比，风机的全压提高了130.70 Pa，效率提高了1.75%。

3.2 不同叶片型线的计算分析

以9-26-10D型离心风机为研究对象，只改变叶片的圆弧半径，保持叶片的其它参数不变。原始离心风机的叶片圆弧半径r为125 mm，现将圆 弧 半 径进行改变，分 别 为 87.5、100、112.5、137.5、150 mm。通过数值模拟计算得到的性能曲线图如图4所示。

图4 离心风机性能曲线：（a）流量-全压性能曲线，（b）流量-效率性能曲线Fig.4 Performance curves of centrifugal fan：（a）flow-full pressure；（b）flow-efficiency

图4（a）为不同叶片型线方案流量—全压性能曲线图，由图4（a）可知：不断地增加离心风机的流量时，风机的全压会随着减小。通过离心风机性能曲线可以得知，当叶片圆弧半径为112.5 mm时，风机模型内部流场的全压明显高于原始模型和其他方案。

图4（b）为不同叶片型线方案流量—效率曲线图，由图4（b）可知：离心风机的效率随着流量的增加而呈现出先增加后减小的趋势。在小流量阶段，气体只占叶片流道的一部分，容易产生涡流和回流等现象，这会造成一定的流动损失，因此这一阶段的效率不高。当离心风机达到合适的气体流量时，气体被充分利用，此时的效率就会较高。当流量较大时，多余的气体会造成摩擦损失，这时效率就会减小。所以，离心风机的效率随着流量的增加而呈现出先增加后减小。通过对比分析可以看出，当圆弧半径为112.5 mm时，风机模型的最高效率高于原始模型和其他改造方案风机模型的最高效率。

该型号离心风机的流量在19 000 m3/h附近时，效率较高。在流量为19 000 m3/h处，其主要性能参数如表2所示。

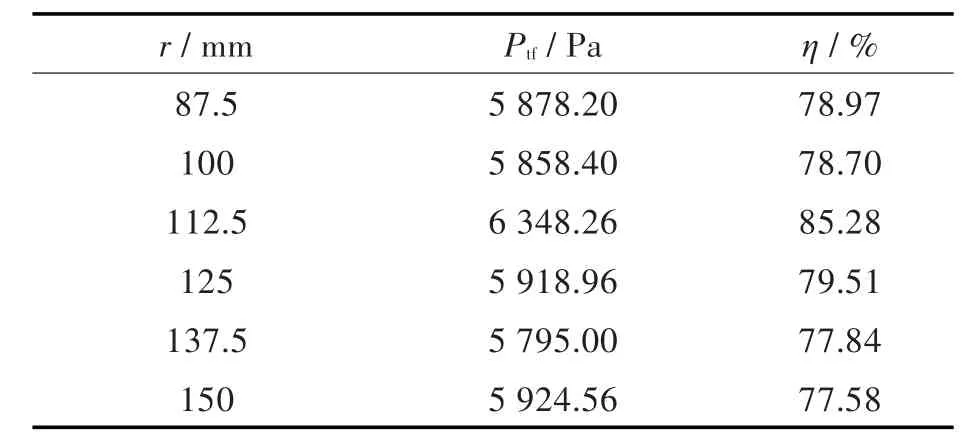
表2 不同叶片圆弧半径在风机流量为19 000 m3/h时的主要性能参数Tab.2 Performance parameters of different blade arc radius at flow rate of 19 000 m3/h

由表2可知：当叶片圆弧半径为112.5 mm时，风机全压为6 348.26 Pa，效率为85.28%；对于叶片圆弧半径为125 mm的原始模型，其风机全压为5 918.93 Pa，效率为79.51%。因此，与原始模型相比，风机的全压提高了429.33 Pa，效率提高了5.77%。

4 结 语

1）通过观察风机全压云图可知，在叶片流道中的压力梯度最大，在叶轮尾部压力最大。全压的变化规律与静压、动压的变化规律基本一致。

2）叶轮流道内气体的速度沿着流动方向不断提高，直至蜗壳流道扩大，速度开始逐渐减小，最终在风机出口处气体速度降到最低。

3）根据数值模拟获得的风机性能数值可以看出，离心风机的全压和效率会随着叶片数目的增多而提高，当叶片数量达到18片时，该型号离心风机的效率得到明显提高，继续增加叶片数量，效率虽会增加，但是增加得并不明显。

4）通过改变叶片型线，对离心风机的数值模拟计算结果进行分析可知，将原离心风机叶片的圆弧段半径改变为112.5 mm时，可以有效提高离心风机效率。

5）对于各种型号离心风机的叶片，也可以通过这种方法进行优化设计分析。