距离约束的网格曲面曲线设计方法∗

金 耀,宋 丹 ,俞成海,马文娟 ,宋 滢 ,何利力

1(浙江理工大学 信息学院,浙江 杭州 310018)

2(天津大学 电气自动化与信息工程学院,天津 300072)

在网格曲面上进行曲线设计是进行几何处理与编辑的一项重要内容,且有着广泛的应用背景,如网格处理中的部件分割[1,2]、虚拟手术中的模拟切割[3,4]、制造业中的图案设计[5-7]以及流形上的计算几何[8-11]等.这种曲线有多种设计方式,其中常见的有插值与光顺两种:用户在网格曲面上输入几个控制点或一条初始曲线,系统便生成一条附着于曲面的光滑曲线,使之经过这些输入点(插值)或逼近于初始曲线(光顺).换言之,在网格曲面上设计曲线,需同时满足流形约束(曲线位于曲面上)、光滑约束、插值点约束(若有)等,而其中的流形约束使其较之于欧式空间的曲线设计问题更为复杂,难度更大.

现有针对网格曲面的曲线设计方法大致可以分为3 类:投影法[12-14]、光顺法[1,2,4]以及参数化法[6,15].投影法通常将光滑的空间曲线迭代地投影到网格流形上,方法简单、高效,但其迭代过程缓慢且投影步骤往往不太鲁棒.光顺法即对给定曲线在保持流形约束下进行光顺,方法通常较为鲁棒,但其效率较低.参数化法即将局部曲面参数化到欧式平面,在平面上设计曲线并将结果映射回曲面,方法往往鲁棒、高效且灵活,但其受限于局部区域,难以进行大范围的曲线设计.

针对上述不足,本文提出了一种高效且实用的曲线设计方法.该方法的思想是:将流形约束转化为距离约束,用切平面逼近局部曲面,将距离约束松弛为点到切平面的距离,并与光滑约束、插值点约束共同作为优化目标进行求解.求解时采用“整体-局部”交替迭代的思想,并借助Gauss-Newton 法控制其收敛行为.该方法不仅提高了鲁棒性与计算效率,而且具有形状可控、适用范围更广等特点,能够应用于多种场合.

1 相关工作

曲线设计是计算机图形学与计算机辅助设计的一个充满活力且具有较长历史的研究话题,现有的大部分研究工作着眼于欧氏空间的曲线设计,其相关的理论与算法被深入研究并已趋于成熟[16,17].随着数字几何的广泛应用以及工业界与学术界需求的增加,在流形空间,尤其是在曲面上进行曲线设计,越来越多地引起人们的关注.但是,针对这类方法的理论与算法未及前者成熟.根据曲面表示形式的不同,这些方法可分为两大类:针对参数曲面的方法与针对网格曲面的方法.前者通常采用参数化法:由于参数曲面具有一个天然的参数域,因此通常可在参数域上设计曲线并将结果映射至原曲面空间[18-20].但是绝大多数方法仅考虑具有单个参数域的参数曲面,对于形状与拓扑复杂的曲面则不适用.由于在实际应用中网格曲面更为广泛,因此本文仅讨论与研究内容相关的针对网格曲面的工作.

网格曲面上的曲线由于其所在的曲面具有分段线性特点,通常表示为一条分段线性的折线段.其中,具有广泛应用背景的离散测地线便是其中一种,且一直是图形学相关领域的研究热点[9-11].但测地线旨在计算“局部最短”的曲线,而本文所研究的是离散曲面上的“光滑”曲线,因此本文仅考虑网格曲面上自由曲线的设计.现有方法大致分为以下3 类.

· 投影法

这类方法将流形约束进行松弛,首先生成经过插值点的光滑曲线,然后将其迭代地投影到流形上.Hofer 等人[12,13]提出了一种基于能量极小化的样条曲线插值方法,他们将曲线离散成折线,把问题描述成一个带流形约束的优化问题,其中,目标函数是样条能量与测地能量的组合;并采用投影梯度法进行求解,即将松弛流形约束得到的空间曲线迭代地投影到曲面上.该方法与流形的表示形式无关,可用于诸如隐式曲面、参数曲面与网格曲面等,但其投影步骤并不能保证一定能找到理想的投影点,鲁棒性较差.同时,由于投影采用了移动最小二乘法(MLS)局部拟合法,效率较低.Pottmann[14]随后提出了高阶样条能量,并将该方法进行推广在曲面上拟合曲线.Wallner 和Pottmann[21]分别提出两种方法,将欧氏空间中设计细分曲线的线性细分法推广至流形曲面:第1种提出用“测地平均法”替代传统的线性平均法,但需计算大量的测地线,较为耗时;第2 种是在外围空间设计细分曲线,然后将结果投影到曲面上,但是投影算法对于复杂曲面并不鲁棒.Morera 等人[22]与Sarlabous 等人[23]均采用测地细分策略,分别提出测地Bézier 曲线与测地圆锥Bézier 曲线的细分曲线生成算法.该方法虽然鲁棒,但涉及到测地线的计算,时间复杂度较高.刘斌等人[5]提出了一种测地B 样条插值方法,通过插值点反求控制点,并运用最近点投影法将其映射到网格曲面上,然后采用插值误差反向补偿法使曲线逐渐逼近曲面.但该方法同样耗时且投影算法可能存在多解,从而无法处理复杂曲面.Bock 等人[24]为生成曲边网格,在线性网格边上采样点,将其投影到曲面上,并对投影点运用高阶样条拟合,其中,投影使用了光滑的Phong 法向场,但生成曲线并不要求严格地位于曲面.Panozzo 等人[25]借助Frechet 均值定义,将欧式空间的加权平均法推广到流形空间,并用于设计样条曲线.他们把网格曲面嵌入到高维空间并在该空间进行加权平均,然后采用Phong 法向场将其投影到嵌入网格.该方法无需迭代且所得曲线光滑性好,但其高维嵌入步骤极为耗时.综上所述,投影法直观且易于实现,但在计算效率或鲁棒性方面表现较差.

· 光顺法

这类方法通常被用于优化特征边,往往首先松弛光滑约束,然后在光滑能量驱动下对初始曲线进行光顺,并保持曲线始终在曲面上.Jung 等人[26]将图像中的主动轮廓模型用于网格曲面,对分割线进行光顺,通过优化表示曲线形状的内部能量和网格特征的外部能量迭代地演化曲线.Benhabiles 等人[27]改进了该方法中的外部能量,对其进行平均和归一化处理,所得到的曲线能够更好地与特征边对齐.Kaplansky 等人[2]采用测地流方程光顺封闭曲线,通过修改扩散准则(方程)以适应不同需求.Wu 等人[28]与Zhang 等人[29]基于测地曲率流方程演化曲线形状,得到了较好的结果,但其效率难以达到交互要求.由于这些方法所生成的曲线均沿着网格边,虽然对于提取特征边有益,但难以设计一般的光滑曲线.Ji 等人[1]也采用了主动轮廓模型,通过构造新的蛇形能量,并结合曲线节点分裂、移动和移除等拓扑操作使曲线能够穿越网格面片,所构造的曲线更为光滑.Lawonn 等人[4]提出了一种网格域曲线的拉普拉斯光顺算子,通过降低曲线的测地曲率以平滑曲线.该方法能够控制曲线的光滑度以及与初始曲线的贴近度,但是由于采用了局部光顺策略,需要较多的迭代次数且无法插值控制点.总而言之,这类方法鲁棒性较好,所设计的曲线通常具有良好的光滑性,但是由于在严格的流形约束下进行光顺,导致其效率低下,且难以用于设计插值曲线.

· 参数化法

这类方法运用平面局部参数化方法,在参数域进行曲线设计,并将结果映射到原曲面.Lee 等人[15]提出了“几何蛇形”法演变曲线形状:他们对初始曲线所在的局部区域进行参数化,并在参数域上运用蛇形能量演化曲线,并将结果映射回网格空间.进而基于极小化原则与局部显著性提出“智能剪刀”法,并用于网格切割[30].朱文明等人[31]采用保角映射构造参数域,并在参数域上生成细分曲线,最终将结果映射回网格曲面.刘斌等人提出了基于指数映射的测地B 样条曲线设计方法[6,32],他们将源曲线控制顶点映射到切空间,根据曲线迁移前后控制顶点法保持坐标不变的原则,建立曲线迁移前后控制顶点的对应关系,实现曲线的几何变换与样条曲线阵列的构造.但该方法仅限于局部区域,且需频繁更新参数域.这类方法可照搬欧式空间的曲线设计方法,简单且灵活,然而现有方法大多考虑局部参数化方法,难以设计大范围的曲线,且未曾考虑参数化形变误差对结果的影响.

本文提出的方法属于投影法,但它将流形约束松弛为点到切平面的距离约束进行求解,克服了上述3 类方法存在的缺点:相比于传统的投影法,该方法同时优化光滑与流形能量,使曲线能够逐步光顺的同时,稳步地贴近曲面,从而使投影步骤的鲁棒性和可靠性大为提高;相比于光顺法,该方法由于松弛了流形约束,优化自由度更大,且计算效率更高;相比于参数化法,该方法能够处理局部参数化法难以适用的具有复杂拓扑的网格曲面.

2 曲线设计方法

2.1 问题描述

给定一个嵌入于三维欧氏空间R3的光滑曲面S以及一堆有序点阵{pj}⊂S,要求一条位于该曲面上且插值于{pj}的光滑曲线c∈S.若采用参数方程表示曲线:c(t)→R3,并运用3 次样条能量度量曲线的光滑度[12,15],则求解曲面上的光滑插值曲线问题可转化为计算如下位置与流形约束下的优化问题:

其中,x(t)∈S表示位于曲面S的曲线,x″(t)为曲线关于位置参数t的二阶导,其几何意义与曲线的曲率正相关.

当S为网格曲面时,其上的曲线可表示为分段线性的离散曲线c=〈V,E〉,其中,V={q1,q2,…,qn}⊂S为曲线上的顶点集,E为形成曲线的边集.

·当曲线为开曲线时,E==1,2,...,n-1}⊂S;

·当其为闭曲线时,E==1,2,...,n}⊂S(%为取模运算).

由于曲线是离散的,公式(1)中曲线的二阶导数x″(t)并不存在,因此需首先对该公式进行离散化,并采用数值方法进行求解.

2.2 流形约束转化

对于离散网格曲面S,由于其没有解析表达式,导致公式(1)中的流形约束难以显式表示,从而给求解该带约束的优化问题带来较大的困难.为此,本文引入一个距离函数D:R3×S→R,用于度量空间中任意点到流形S的距离,从而将流形约束转化为距离约束,即等价地表示为曲线上任意点q∈x(t)到曲面S的距离为0:

而距离函数D则可定义为点到局部曲面的最短距离:

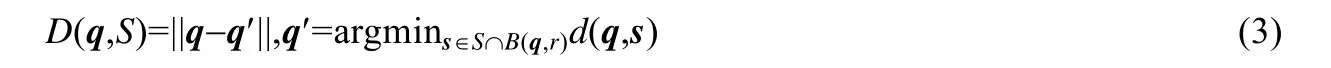
其中,d为点到点的欧式距离函数,B(q,r)为q的半径为r的球形邻域.

2.3 离散化

公式(1)中带约束的优化问题可用数值方法求解,但首先需进行离散化.为方便对二阶微分表示的3 次样条能量进行离散化,类似文献[12],本文采用弦长参数化方法计算采样密度,即对相邻两个插值点所形成的线段pi pi+1,确定其采样点个数Ni为

其中,D为离散步长,亦即每条线段的长度(默认情况下设置为网格平均边长的五分之一),用于控制曲线的采样密度.由此,该曲线可离散成折线段,其有序采样点为{qj},其中,=pi(ki为插值点在采样点中的序号).由于该离散方式使得曲线上的采样点能近似均匀分布,因此公式(1)的目标函数可近似地离散化表示为均权拉普拉斯能量[33]:

其中,对于开曲线,M表示折线段中除却首尾端点的离散点个数;而对于闭曲线,M表示所有离散点个数.于是,公式(1)可改写为如下离散表达式:

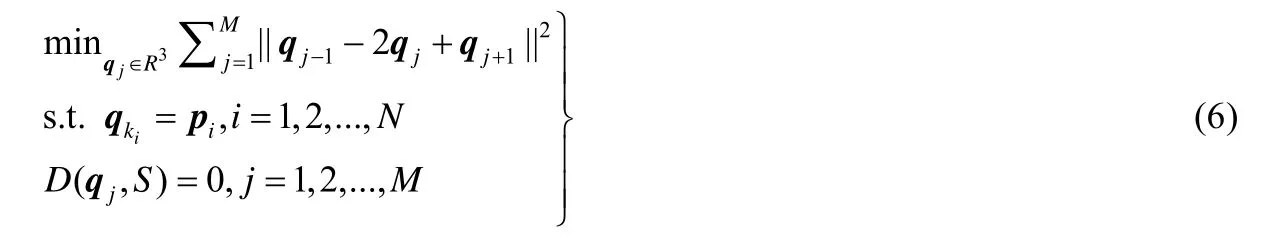
为求解该问题,本文运用罚函数法,结合距离公式(3),并将公式(5)中硬约束表示的插值点约束与流形约束分别作成软约束,则公式(5)进一步转化为如下优化问题:

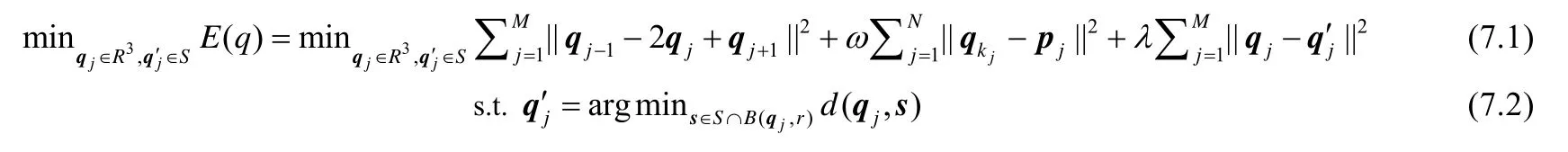
其中,

· 参数ω默认取作大的数值(108),使之近似满足插值约束;

·λ由用户控制,用于平衡光滑性与流形约束的满足程度.

2.4 数值求解

由公式(7.1)、公式(7.2)所定义的优化问题可知:每一对qj与j′q都是彼此相关的,其非线性程度较高,因此直接求解难度较大.为此,本文计算相邻插值点之间的Dijsktra 路径作为初始曲线,根据公式(4)所得的采样点数量在曲线上均匀采样离散点{qj},并设置{q′j}={qj};然后借鉴局部/整体交替迭代的优化策略[34]进行求解,即将该两组优化变量进行分离,并把每次迭代分解为整体阶段和局部阶段,直至前后两次计算得到的曲线差异很小为止,其计算过程如下.

整体阶段.固定{q′j},求解{qj}.此时即计算能量函数(7.1)的极小值.由于该式是关于{qj}的二次函数,因此可转化为矩阵方程组AQ=B,其中,A为常系数矩阵.

局部阶段.固定{qj},求解{q′j}.此时对每一个qj,求解问题(7.2),即在qj的球形邻域与网格曲面的交集中搜索最近点.由于计算球体与网格的交集以及在该交集处的最近点较为耗时,因此可采用拓扑邻域替代球体几何邻域,即将前一次迭代得到的投影点(n为迭代次数)所在三角形面片f0的r-环拓扑邻域的面片集合F作为交集.在该交集中,搜索qj到该局部区域的最近点距离:

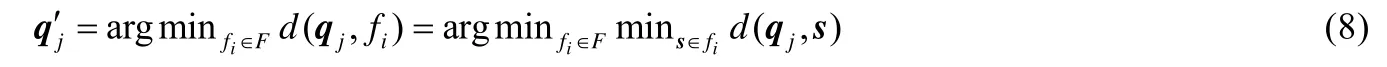
其中,点到三角形的距离d(qj,fi)可采用文献[35]中介绍的方法.具体地,以f0作为种子点,以广度优先的方式遍历F,对每个面片计算该点在面片上的法向投影:若投影点在其内部,则将其作为投影点并结束搜索;否则,计算点到面片的距离并更新最近点,直至遍历完所有面片.当局部区域非凸时,有可能存在多个最近点,此时可选取使局部拉普拉斯能量,即最小的最近点作为候选点.

易证,上述交替迭代的优化策略可使能量函数(7.1)单调下降,从而收敛.具体地,在每一次迭代中,其整体阶段求解能量函数极小值能获得比当前能量更低的值;而在局部阶段,由于固定{qj},能量函数(7.1)的前2 项为常数,第3 项由于D(qj,S)≤||qj-q′j||,因此也能得到更低的值.从而对于每一次迭代,该策略均将使能量值下降.

但由于q′j由前一阶段曲线采样点计算得到,而非当前qj的投影点,直接用欧式距离||qj-q′j||度量点到曲面的距离并不精确.因此,上述算法虽能收敛,但收敛速度较为缓慢.本文采用该方法在骆驼头模型上设计一条经过3 个插值点的闭合曲线,如图1 所示.随着迭代的进行,曲线变得越来越光滑,但其变化过程缓慢,迭代次数过多.虽然该算法在理论上是收敛的,且其整体阶段仅需高效地回代计算更新曲线坐标,但由于其局部阶段的投影计算耗时相对较多,若迭代次数过多将严重影响计算效率.在本实验中,达到最大迭代次数(1 000)依然未能收敛.

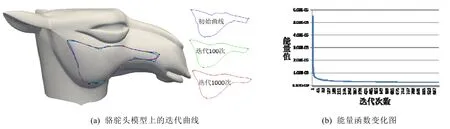
Fig.1 Iteration results and its energy graph with point-to-point distance constraints (λ=0.1)图1 基于点到点距离约束的迭代结果与能量图(λ=0.1)

为此,本文借鉴用于曲面配准的迭代最近点(ICP)[36]的算法思想,用对应点处的切平面逼近局部曲面,并采用点到切平面的距离近似度量点到曲面的距离.设q′j处的切平面为Tj,其对应的法向为N(q′j),则qj到曲面S的距离可近似表示如下:

其示意图如图2 所示.

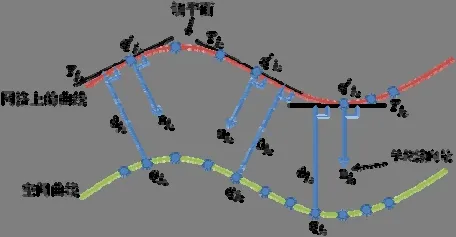
Fig.2 Illustration of the distance from a point to its tangent plane图2 点到切平面距离的示意图

从而,公式(7.1)可近似转化为如下优化问题:

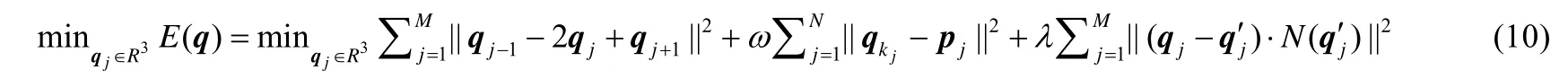
相对于点到点的距离约束,点到切平面的距离约束由于约束曲线采样点在近切平面上移动,使得一方面给予其足够的自由度进行光顺,另一方面又能贴近网格曲面,因此能够较快地实现曲线的光顺.

类似基于点到点距离约束的数值方法,本文同样采用“整体-局部”交替迭代的策略求解公式(10).然而,若直接采用该策略,将可能导致曲线在整体阶段“过度”光顺而偏离曲面,且不能保证算法收敛——虽然能量函数值在整体阶段得到下降,但在局部投影阶段可能上升.为此,本文借助Gauss-Newton 法[37]的思想,采用局部线搜索控制其收敛行为.利用公式(10)的Hessian 矩阵H(E(q))计算当前曲线顶点的迭代方向,并结合线性回溯搜索法控制迭代步长.即:当能量函数值大于当前值时,采用对步长折半的方式保证能量函数在迭代过程中单调下降,从而使算法能够稳定收敛.由于公式(10)确定的能量函数为平方和形式,其对应的Hessian 矩阵是对称正定的,因此其每次迭代的“整体”阶段均可转化为凸问题进行求解,无需进行正则化.其迭代求解的每一步通过如下公式更新曲线顶点位置:

其中,ω∈(0,1]为迭代步长,通过折半线性回溯法确定大小.

为了提高计算效率,本文分别从整体和局部阶段两方面进行考虑.整体阶段需求解一个线性系统,利用公式(11)中Hessian 矩阵的结构在迭代中始终保持不变的性质,通过对矩阵结构进行预分解以加速.局部阶段需搜索最近点,本文用切平面法向量与局部邻域面片的交点进行近似,一旦找到交点则结束,不必遍历剩余面片.由于交点不一定存在,此时可采用最近点替代.

由上述算法得到的曲线,其每一段离散的折线将非常接近曲面但往往不严格位于曲面上(对位于不同面片的相邻两个点形成的线段).为此,本文采用文献[38]中介绍的投影法将其映射到曲面上:对于每一条未处于网格表面的线段,由一个端点(起始点)向另一个端点(终止点)逐步构造切割平面,与相关的网格边进行求交,并将交点更新为起始点,逐步往前传播.如此循环,直至起始点与终止点重叠.具体细节可参考文献[38].

综上所述,本文提出的基于距离约束的曲线优化算法可描述如下.

算法1.基于距离约束的曲线优化算法.

3 实验结果与讨论

本文用C++语言实现了上述算法,并在8 核Intel i7-7700U 处理器、8G 内存的Linux 虚拟机环境下运行.其中,算法所涉及的线性方程组的求解采用Eigen 库[39]提供的稀疏Cholesky 分解法——LLT 算法.下面,本文通过一系列实验展示该算法的特点.

3.1 算法的收敛性实验

本文在人脸模型上设计了一条经过3 个插值点的开曲线.该曲线在迭代20 次后收敛,图3 给出了迭代的中间结果.由图可见:随着迭代次数的增加,曲线在曲面上滑动而趋于光滑,最终收敛并达到稳定状态.大量实验结果表明:本算法在步长控制策略的作用下均能稳定地收敛,且在绝大多数情况下均在梯度条件下收敛.

Fig.3 Sampled curves on the face model generated during the iterations (λ=0.1)图3 人脸模型上插值曲线的迭代序列(λ=0.1)

图4 所示为3 个迭代曲线图,分别为能量函数值(公式(10))、对应的梯度模长的平方(施加了log 函数)以及平均距离的变化.随着迭代的进行,能量函数值逐步下降;其梯度值尽管在局部跳动,但总体亦呈现下降趋势;曲线到网格的平均距离值也较为稳定地下降,且当算法收敛时,其平均距离也达到较小值.此时利用投影法将其映射到曲面上,对曲线光滑度的影响较小.

本文算法较为耗时部分为迭代中局部阶段的投影点计算.该算法在前次迭代的投影点所在面片的r-环拓扑邻域搜索投影点.为加速起见,本文采用法向与邻域的交点替代最近点以过滤部分面片方式,并比较了两种策略(r=2),实验结果如图5(a)所示.由图可见:两者所设计的曲线形状较为相似,几乎重合,但法向交点策略迭代88 次,耗时104ms,而最近点策略迭代101 次,耗时431ms.因此,前者能在不影响结果的前提下有效地提升效率.本文同时比较了不同邻域大小对结果的影响,如图5(b)所示(其中的红点为插值点,下同).由图可见:1-环邻域结果与其他结果有一定差异,而2-环与3-环邻域的结果几无区别,三者的迭代次数分别为126、95 与88 次.由此说明,r对算法收敛快慢有一定影响.这是由于r较小时,曲线移动的步长相应减少,因此需要更多的迭代次数到达极小值点;而当r≥2 时,其结果差异较小,虽然能在一定程度上加快收敛,但同时也意味着将增加局部搜索次数.综合权衡算法效率,本文将r默认设置为2.

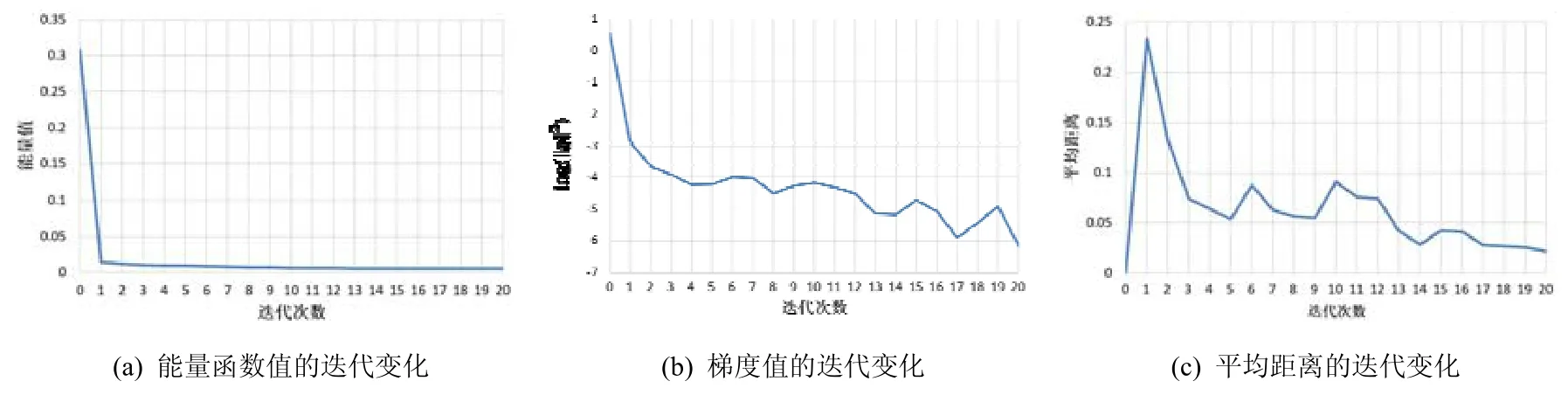
Fig.4 Generated curves during the iteration on the face model图4 人脸模型上曲线的迭代变化过程

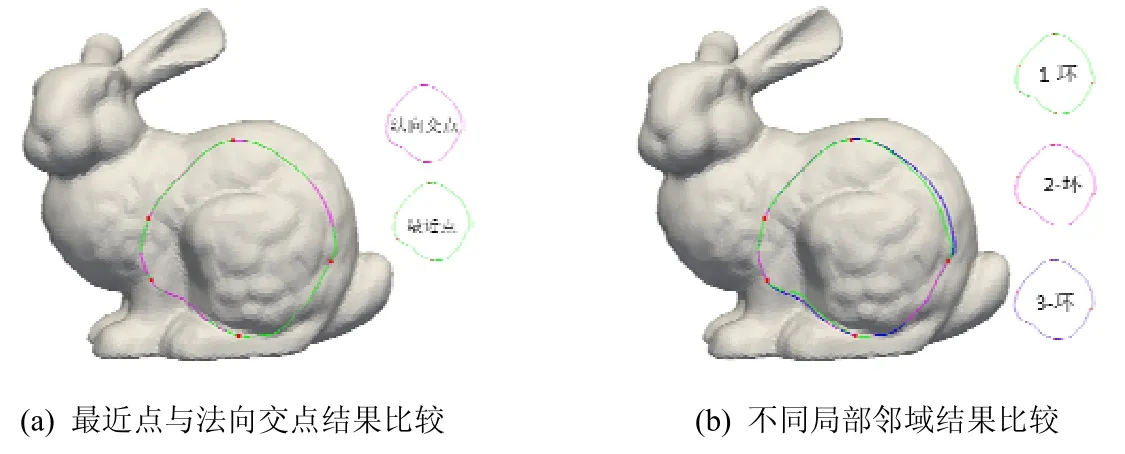
Fig.5 Comparison results with different strategies of local neighboring search图5 采用不同局部邻域搜索策略的结果比较

3.2 可控参数λ

在公式(10)中,参数λ用于平衡曲线的光滑度与流形约束的满足程度.当λ过大时,流形约束能量将占主导.此时,算法行为将与光滑法(例如文献[4])类似.曲线在迭代时易陷入局部极小值,即曲线得不到充分光顺,同时也将增大方程条件数,使得数值性质变差.当λ过小时,光滑约束能量将占主导,此时,算法行为将与传统的投影法(如文献[12])相似.虽然曲线得到了充分的光顺,但是距离曲面较远,投影将破坏曲线的光滑度.当λ取值适宜时,算法将兼具两类方法的优势.图6 展示了插值点相同但λ取值不同情况下,人脸模型上的插值曲线.

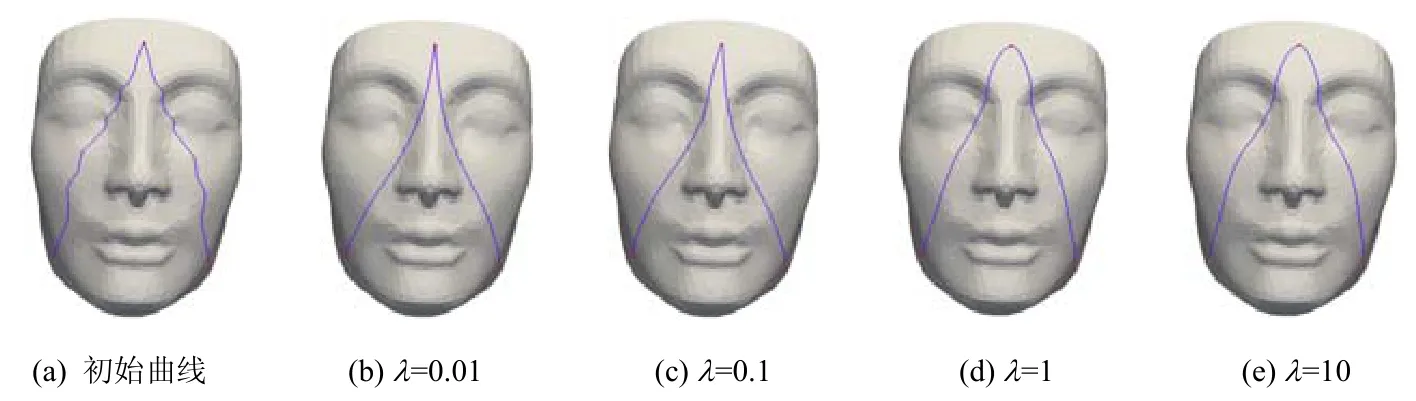
Fig.6 Interpolatory curves on the face model with different values of λ图6 λ取不同值时,人脸模型上的插值曲线

由图可见:当λ取值为1 和10 时,曲线偏离初始曲线较近,未能得到充分光顺;当其取值为0.1 和0.01 时,曲线偏离初始曲线较远,但光滑度得到了改善.为了定量比较各曲线的光滑度,本文采用表示曲线曲率的离散拉普拉斯能量,即公式(5)进行度量.λ从0.01 变化到10,各曲线的光滑度分别为[0.0200,0.0133,0.0237,0.0247].通过大量实验发现,λ=0.1 时获得的曲线能够取得较好的光滑度.因此,本文实验中将参数λ默认取作0.1.

3.3 比较实验

相比于经典的基于能量极小化的投影法[12],本文算法具有众多优点.本文实现了文献[12]中描述的算法(部分参数原文未给出,其结果可能与原文有差异),并与本文方法进行了比较.

· 首先,本文方法效率较高.文献[12]中的方法首先松弛流形约束,然后逐步将其投影到流形上,其中,投影步骤采用了耗时的移动最小二乘法(MLS)估算局部曲率,使得效率大为降低.图7(a)所示为两种方法在雕像上的曲线设计结果,其中,本文方法(右图)耗时117.2ms,文献[12]中的方法(左图)耗时281.9ms(迭代22 次收敛);

· 其次,两者采用同样的离散拉普拉斯能量作为优化目标,但本文方法得到的结果通常比文献[12]的结果更为光滑.文献[12]在逐步投影时并未考虑光滑约束,且最终还需将隐式曲面上的曲线投影到网格上,因此在一定程度上影响了其光滑性;而本文方法中光滑步骤与投影步骤交替进行,且由于曲面上大部分采样点落在网格面上,很多时候实际投影点即为该点本身,因此能够有效地保持光滑性.图7(a)所示结果的光滑性在视觉上的差异并不明显,为此本文采用公式(5)来度量光滑度并对其进行比较:左图的光滑度值为2.49-6,右图的光滑度值为2.76-6;

· 再次,本文方法更为鲁棒.文献[12]在具有尖锐边特征边的模型上设计曲线时,可能因法曲率估算不够准确使其步长估算不正确,从而导致投影错误,使曲线出现较明显的锯齿状(如图7(b)左所示),而本文方法不受特征边影响(如图7(b)右所示).

Fig.7 Comparison results of the algorithm[12] and our method图7 文献[12]算法与本文算法的结果比较

本文同时比较了文献[24]中提出的基于Phong 投影的B 样条设计方法.

该方法首先运用多维尺度变换法(multidimensional scaling)将网格曲面嵌入到八维欧式空间,然后在该空间设计B 样条曲线,并运用Phong 投影法将其映射到嵌入网格上,最后将所得曲线映射回原网格.文献[24]仅给出了B 样条的正向设计方法,即根据控制点设计曲线.为方便比较,本文实现了B 样条的逆向算法设计插值曲线(采用夹持端点条件)[40],并与本文方法进行比较,其结果如图8 所示.由图8 可见:两者结果虽然在曲线外形上存在一定差异,但视觉上均较为光滑.就曲线设计步骤而言,文献[24]由于无需迭代,效率较高,在该实例中(曲线的离散点数目相同)仅耗时1ms;而本文算法耗时6ms.但是该方法需计算点点测地距离与网格的高维嵌入,计算复杂性很高,在实际应用中可能会带来不便.

相比于最新的基于局部拉普拉斯光顺的曲线设计算法[4],本文算法亦具有较大优势.文献[4]的算法有一个参数t∈(0,1],用于控制与初始曲线的逼近程度.为使其具有近似插值效果,将t统一取为1,与本文算法进行比较.首先,本文算法可设计插值曲线与闭合曲线,而文献[4]算法则不能,其比较结果如图9 与图10 所示.图9 比较了两种方法在瓶子与梨模型上所生成的开曲线.前者算法得到的曲线没有经过所有控制点,而本文算法则能插值于控制点;图10 比较了两种方法在脚与狗头模型上所生成的闭曲线.前者算法由于采用了局部拉普拉斯光顺算法,无法处理闭合曲线,因此所生成的曲线在首尾连接处出现尖角,而本文算法得到的曲线则在视觉上处处光滑.同时,前者算法所生成曲线的采样点均在网格边上,无法做到自适应细分,因此其光滑度受到网格分辨率的影响,如图9(b)、图10(b)所示,曲线上的“折角”较为明显.此外,在多数情况下,本文算法效率较高.对于图9、图10 中的4 个例子,本文算法的运行时间分别为27.8、25.4、28.4 与44.0(ms),而文献[4]算法则分别需要123、27、68、14(ms).

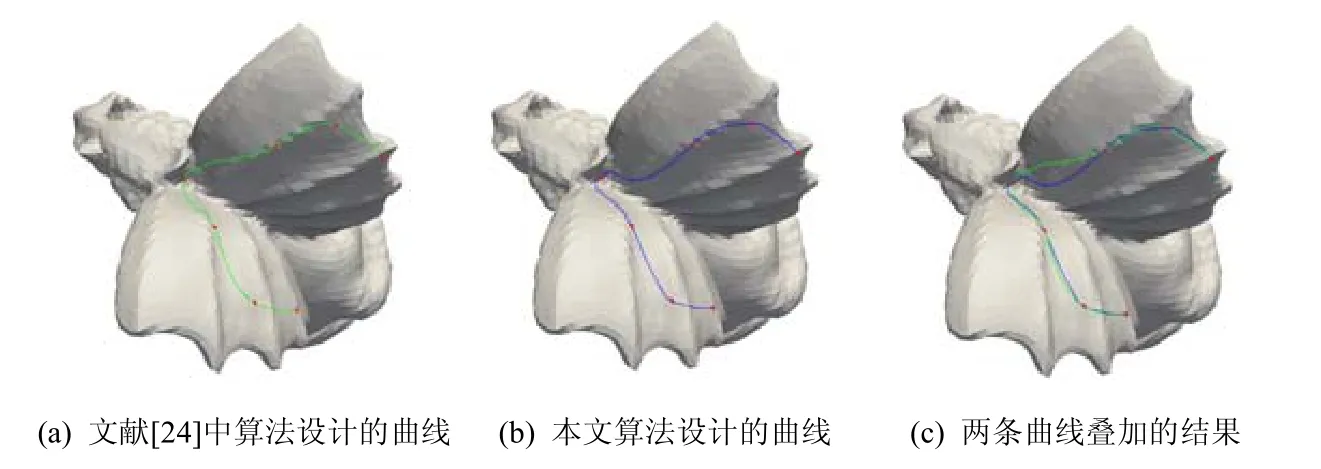
Fig.8 Comparison results of the algorithm[24] and our method on the wings of the gargoyle model图8 文献[24]中算法与本文算法在怪兽翅膀模型的结果比较

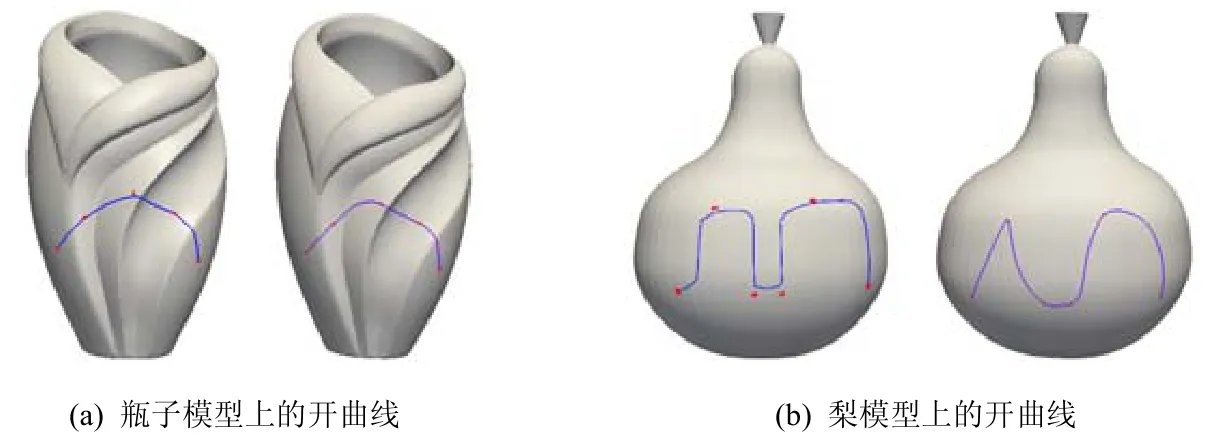
Fig.9 Comarison results for open curves of the algorithm[4] and ours图9 文献[4]中算法与本文算法所设计的开曲线的比较结果

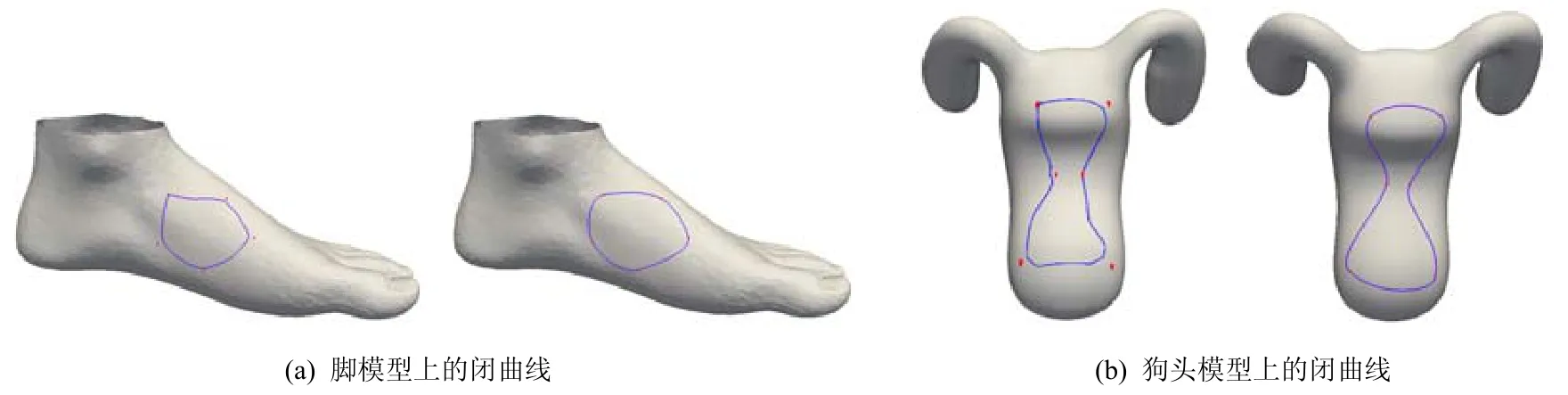
Fig.10 Comarison results for close curves of the algorithm[4] and ours图10 文献[4]中算法与本文算法所设计的闭曲线的比较结果

相比于基于参数化的曲线设计方法[6,15],本文算法适用范围广泛.本文实现了文献[15]中提出的基于参数化的几何蛇形算法,该方法通过优化内部能量和外部能量的组合演化给定曲线.其中,内部能量表示为曲线一阶导与二阶导能量的线性组合,外部能量与网格特征相关;而其二阶导能量即为本文所采用的能量函数(见公式(5)),区别在于该算法在参数域,而本文算法直接在曲面上计算曲线.为在同等条件下进行比较,本文对该算法进行简化,仅运用二阶导能量优化曲线,采用最小二乘共形映射(LSCM)[41]在初始曲线的5-环邻域计算局部参数域.由于该优化方程没有外部能量,因此可简化为线性方程组进行高效求解.图11 给出了具有2 个亏格的“8 字”模型上所设计的曲线的比较结果.由图11(a)与图11(b)的结果可以看出,两者均能在曲面上设计光滑曲线.文献[15]中算法由于无需迭代,在效率上比本文算法更有优势,其仅耗时9ms,而本文算法耗时85.3ms.但是文献[15]无法处理图11(c)所示曲线——其局部邻域需经过切割才能进行参数化,而在切割线处难以保证曲线的连续性.而本文算法可在任意亏格的曲面上自由地设计曲线,与模型的拓扑复杂性无关.

Fig.11 Interpolatory curve on the eight model图11 “8 字”模型上的插值曲线

3.4 应 用

本文方法不仅能够设计插值曲线,且能光顺给定的曲线.该问题即等价于设计逼近于初始曲线c0∈S的光滑曲线.因此仅需对插值曲线模型稍加改造,即将公式(10)中的插值点约束修改成数据拟合项,并以软约束的形式加入到目标函数,使得曲线在得到光顺的同时,尽可能逼近初始曲线,即.其中,为采样自c0与qj对应的点;α可根据实际需求(逼近程度)确定,默认设置为0.01.图12(a)所示为鸭子脖子部位的初始分割线,由于其分割边界由网格边依次相连而成,其曲线形状的锯齿状较为明显;而经过本文算法光顺后,可得到图12(b)所示的曲线,视觉效果上变得更为光滑.

Fig.12 Curve smoothing result on the duck model图12 鸭子模型分割线的光顺结果

本文曲线设计算法可用于多种场合,图13 给出了几个应用实例.其中,图13(a)展示了在鱼身模型上交互勾勒五角星图案的例子;图13(b)给出了在牛模型的身体部位切割孔洞的例子,可用于虚拟手术,观察器官内部环境;图13(c)所示为部件切割的例子,可用于交互分割模型部件.

Fig.13 Applications of our curve design method图13 曲线设计的应用实例

本文算法最为耗时的部分为迭代中所涉及的线性方程组的求解与局部投影计算.由于该算法在整体与局部阶段均采用了加速策略,因此求解效率相对较高.表1列出了在各个模型上设计曲线的运行时间.由表1可见:算法效率与网格模型的规模相关度较小,而主要取决于曲线的离散采样点的数目,且总体效率可满足交互应用的要求.

Table 1 Cost time of generating curve on various models表1 各个模型上曲线的生成时间

4 结 语

本文提出了一种针对网格曲面的高效且实用的曲线设计方法,该方法将流形约束松弛为点到切平面距离的约束,并将所有约束共同描述成一个优化问题进行求解.该方法鲁棒、高效,适用范围广,可用于任意复杂拓扑(如多亏格)的网格曲面.此外,相比于前沿算法,本文方法不仅能够设计闭合与开曲线、插值与光顺曲线,而且在效率上占有明显优势,能够满足交互响应要求.

本文方法通过采用局部线搜索策略控制迭代步长,能够保证算法收敛,但是该策略由于对步长进行了限制,有时未能充分松弛曲线形状,从而可能陷入局部最优解.在今后,我们将探索更好的收敛策略,在保证收敛性的同时,更好地控制曲线形状.此外,本文算法的复杂度与曲线采样点的个数相关,对于设计采样密度较大的曲线,其效率将成为一个瓶颈.因此,这也是未来需要研究的工作.