竖直平面激波与水平热层作用后流场的理论计算方法研究*
贾雷明,田 宙
(1. 清华大学工程物理系,北京 100084;2. 西北核技术研究院,陕西 西安 710024)
在爆轰激波管[1]或强爆炸[2]等环境中,激波阵面或爆炸火球释放出的热辐射,先于激波到达固壁表面并发生能量沉积,致使壁面附近形成具有较高温度的气体层,称为“热层”(thermal layer)。由于热层内气体声速大于周围空气,热层内激波阵面会超越空气中激波阵面传播,导致流场中出现前驱波和涡旋等结构。与不考虑热层时的情形相比,固壁附近的流场参量也会发生改变。因此,激波与热层作用常被应用于流场诊断和控制[3-5]。
为了认识激波与热层作用机制,人们针对不同形式的激波与热层作用,开展了大量的实验和数值模拟工作[6-18]。在理论分析方面,已有的工作则主要关注竖直平面激波与水平热层作用,在这类作用中,热层高度是唯一的长度尺寸,随着激波传播距离远大于热层高度,流动会进入准自相似阶段,流场结构近似呈比例发展,此时可假定流动定常,从而使理论分析简化。
最早,Griffith[6]针对热层与周围空气物性差异较小的情形,在与入射激波固连的坐标系中,假定流动定常,采用线性小扰动理论求解二维定常Euler 方程组,得到了激波阵面形状和波后流场参量分布。针对热层与空气物性差异较大的情形,小扰动方法不再适用,因此人们又建立了新的理论方法,主要用于计算固壁附近的流场参量。Shreffler 等[7]将热层高度近似为零,认为入射激波后的流体在一维简单稀疏波的作用下膨胀加速,形成沿固壁运动的楔形“活塞”,驱动物质界面偏折和前驱波传播;在与楔形“活塞”固连的坐标系内,假定流动定常,给定前驱波传播方向,就可以求得楔形“活塞”内流体的压力和速度。但是,该理论方法不能计算热层内的激波强度,且需利用实验或数值模拟确定前驱波传播方向。Hess[19]和Mirels[20]等则认为,随着流动进入准自相似阶段,热层内激波传播速度应与入射激波传播速度相等,由此计算热层内激波的强度。为了计算固壁附近的流场参量,Mirels[20]进一步假定:(1)在与入射激波阵面固连的坐标系中,入射激波后流体在定常等熵波作用下膨胀加速,形成沿固壁运动的“活塞”;(2)在与热层内激波阵面固连的坐标系中,穿越激波后的热层气体在定常等熵波作用下减速增压,直至与“活塞”内流体压力相等,而速度则满足一定的线性比例关系。但是,速度比例系数依赖于具体的工况条件,需借助于实验或数值模拟确定;同时,在流动准自相似阶段,热层内激波速度会趋近于某一值,而该值通常大于入射激波速度。
综上,Shreffler[7]、Hess[19]和Mirels[20]等的理论方法均基于某种流动定常假定,且由于未对热层内激波传播进行详细求解,这些方法大都依赖于特定的经验参数,而经验参数又需要借助于实验或数值模拟确定。本文中围绕竖直平面激波与水平热层作用,对Mirels[20]理论方法进行改进:(1)分析热层内激波传播过程,然后基于激波动力学理论计算热层内激波传播,从而舍弃“热层内激波速度与入射激波速度相等”的假定;(2)考虑到整个流场是在入射激波后流体而非入射激波的推动下发展,因此在与入射激波后流体固连的坐标系中,假定入射激波后流体在定常等熵波作用下形成沿固壁运动的“活塞”;(3)“活塞”内流体与其毗邻的热层气体,应满足压力和速度连续,从而不再引入速度比例系数。本文中将通过与数值模拟结果、实验数据和已有理论方法的结果进行对比,验证上述改进的合理性。
1 理论计算方法
初始时刻,固壁附近布有性质均匀的水平热层,其高度为h,并与周围空气处于等压静止状态,见图1(a),图中实线表示激波,短划线表示物质界面。在t=0 时刻,竖直平面激波I 到达热层左侧界面处,并与之发生作用,产生透射激波T 和反射波R。波T 和R 分别向物质界面左右两侧传播,见图1(b),图中点P1为波T 阵面与热层上侧界面的交点。记波I 和T 的传播速度分别为DI、DT,由于DT>DI,当波T 超越上方空气中的波I 后,位于波T 后的高压流体会向上方空气中膨胀,驱动形成透射激波P,该透射激波P 被称为“前驱波”,见图1(c)。同时,由于激波与热层界面作用存在斜压效应,即 ∇p×∇ρ ≠0,流场中会有涡量产生并沿物质界面沉积,最终在流场不稳定性的影响下,形成涡旋。与不考虑热层时的情形相比,流场演化更加复杂。
1.1 热层内透射激波传播
在t=0 时刻,波T 和R 后的流场参量可借助于一维Riemann 问题的精确求解方案[21]给出。
在t>0 时刻,波T 超越波I 沿热层上侧界面传播。由于初始时刻波T 阵面与热层上界面垂直,因此波T 沿热层上侧界面的折射为非正规折射。本文中利用Whitham 提出的几何激波动力学(geometrical shock dynamics,后文简称为GSD)理论[22-23],计算波T 沿热层上侧界面的非正规折射。GSD 理论常用于近似求解二维/三维激波阵面的传播。
非正规折射的发生,是因为波后流场中的扰动追赶上了波T。记波T 独自沿热层上侧界面折射(即不考虑波I 的存在)时,点P1沿界面的移动速度为DP1。如果DP1>DI,则波T 沿界面的折射仅与波T 强度和界面两侧的物性参数有关;如果DP1<DI,则波T 沿界面的折射还会受到波I 的影响。接下来,分别对这两种情形进行讨论。
1.1.1 折射不受波I 影响
此时,在点P1附近,热层气体经过波T 后压力增加,然后向上方空气中膨胀,形成前驱波P 和反射稀疏波R1;稀疏波R1沿波T 阵面传播,使得波T 强度减小、波阵面发生弯曲,记弯曲后的波阵面为波T′;在热层上方,前驱波P 与波I 作用,形成激波R2、R3、T1和新的物质界面,见图2,图中实线表示激波,短划线表示物质界面,点线表示稀疏波。

图2 波T 沿界面的非正规折射(DP1>DI)Fig.2 Irregular refraction of wave T at the horizontal material interface (DP1>DI)
依据GSD 理论,建立波T 与T′之间的近似关系,

式中:Ma为激波马赫数,θ 为激波传播方向与水平方向的夹角,A=A(Ma)为射线管面积函数,下标T、T′分别表示波T 和T′的相关参数。本文中约定,所有的角度均以逆时针方向为正。
在点P1附近,波T′后流场并不均匀,因此不能利用双波或三波理论来求解点P1附近的流场。考虑到扰动是从界面下方的流场中产生的,然后跨越界面向上方流场传播。当稳定的折射结构形成时,在点P1附近,波P 与波T′阵面应保持连续,且流场不再发生变化。此时,界面下方流场中的扰动不会再跨越界面向上方传播,否则波P 后流场将再次发生改变。因此,界面下方流场中扰动与波T′阵面交点的运动轨迹应与波后物质界面重合,即

式中:αT′为扰动运动轨迹与水平方向的夹角,δT′为波T′后物质界面与水平方向的夹角。根据GSD 理论,有

式中:

γ 为比热比。建立与点P1固连的坐标系,记为 ℜ1,根据斜激波关系式,有

式中:ξ 为波T′后压力与波前压力之比,Ma0为坐标系 ℜ1中波T′前流场马赫数。波T′与P 阵面在点P1处保持连续,且波后流场压力相等,再联立式(1)~(4),即可求得点P1附近波T′、P 后流场以及点P1沿界面的传播速度DP1。
在热层上方,可利用激波关系式求解波P 与波I 作用后的流场分布。
1.1.2 折射受波I 影响
当DP1<DI时,波T 沿界面的折射会受到热层上方波I 的影响。此时,除了在界面下方流场有稀疏波产生外,在界面上方的流场中还产生了压缩波,记为R4,它会沿着波I 阵面向上传播,使得波I 阵面向前弯曲,形成前驱波P,见图3。流动本身具有极强的非线性,随着时间发展压缩波R4会逐渐演化成激波,并与波I 和P 组成三波结构,类似于斜激波在固壁的马赫反射。三波点附近的流场近似采用三波理论描述。
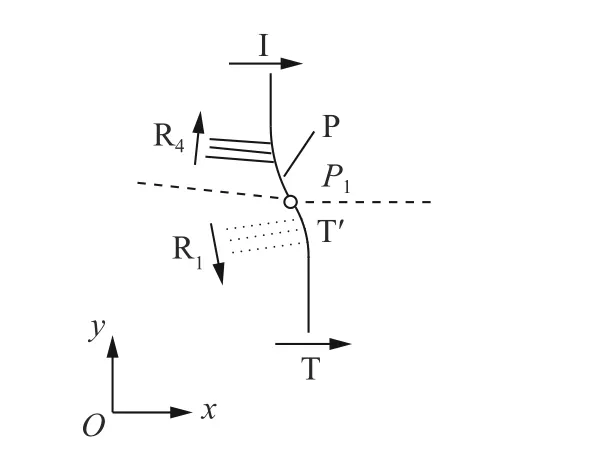
图3 波T 沿界面的非正规折射(DP1<DI)Fig.3 Irregular refraction of wave T at the horizontal material interface (DP1<DI)
波T 与T′之间仍近似满足式(1)。在点P1附近,由于折射受到波I 的影响,因此式(2)不再成立。本文中采用Catherasoo 等[24]建立的激波在非均匀介质中的传播理论,描述界面两侧波T′和波P 参数所满足的关系,有
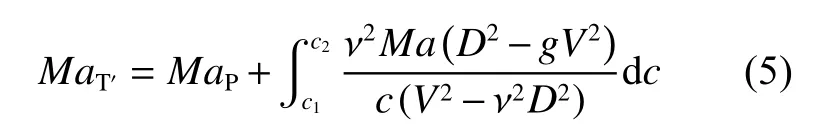
式中:MaP为波P 的马赫数,c1、c2分别为波前未扰动空气和热层气体的声速,

式中:DP为波P 传播速度,θP为波P 传播方向与水平方向夹角,其余物理量意义同式(3)。假定波P 阵面保持平直,联立式(1)、(5)和三波理论,即可求得点P1附近波T′和P 后的流场。
上述理论方法适用于波R1到达固壁之前的时刻。记波T 后流场声速为cT,在t=h/cT时,波R1到达固壁并发生反射,形成新的反射稀疏波,稀疏波后激波阵面仍保持与固壁垂直,可利用式(1)求解激波参数。在t>h/cT时,新的反射稀疏波会沿着波T′阵面向上传播。当反射稀疏波到达热层上侧界面后,又会发生反射,流场可利用上述理论方法进行求解。新生成的反射稀疏波又会向着固壁运动。如果忽略流场中其他扰动的影响,这个过程会不断持续下去,热层内激波阵面的构型也会发生周期性变化,激波强度逐渐减小,见图4,图中t1~t5表示不同的时刻,点划线表示稀疏波与波T 阵面交点轨迹,为了记述方便,将任意时刻热层内激波阵面统一记为波T。真实情况中,流场左侧的扰动势必会赶上波T,图4 所示的过程并不会一直持续下去。

图4 热层内激波传播Fig.4 Shock propagation with time in the thermal layer
1.2 固壁附近流场
当激波走过的距离远大于热层高度h时,流动进入准自相似阶段。此时,流场参量可以近似看作是变量x/t和y/t的函数。将固壁附近流场划分成五个区域,见图5,其中区域1 是驱动涡旋发展的流体区域,区域2、3 是涡旋区域,涡旋与固壁之间的流体即为沿固壁运动的“活塞”,区域4 是经过波T 压缩后的热层气体,区域5 是处于未扰动状态的热层气体。图5 中,点P1为波T 与热层上侧物质界面的交点,点P2~P5为区域1~5 的分界点。
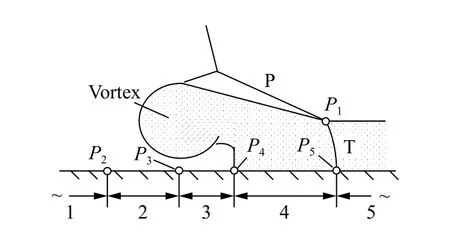
图5 固壁附近流场区域划分示意图Fig.5 Illustration of flow field division near the wall
在区域1 中,初始时刻波I 与界面作用形成反射波R,波R 沿固壁向界面左侧传播。由于pR≠pI,界面附近又会产生扰动分别向热层上方和固壁传播。这些扰动传播的结果,是使得流场恢复到均衡状态,本文中近似选取波I 后流体状态作为均衡状态。
在区域2、3 中,物质界面与固壁组成了收缩-扩张管道,点P3处为收缩与扩张管道的连接处。区域1中的流体先经过收缩管道进行加速减压,再经过扩张管道减速升压后,到达点P4附近。建立与区域1中流体固连的坐标系 ℜ2,在坐标系 ℜ2中观察区域2、3 处的流动,假定流动满足准一维定常绝热条件,有

式中:ρ 为密度,u为速度,下标2、4L 分别表示点P2和点P4附近界面左侧的流场参量。点P2附近流场参量即为区域1 中流场参量。
在区域4 中,热层气体穿过波T 后,压力和速度增加。波T 与固壁相交于点P5,建立与点P5固连的坐标系 ℜ5。 在坐标系 ℜ5中观察,物质界面、固壁与波T 组成扩张管道,假定管道内流动满足准一维定常绝热条件,则有

式中:下标4R、5 分别表示点P4附近界面右侧、点P5附近的流场参量,D5为波T 沿固壁的运动速度。在点P4附近,界面两侧流场满足连续条件,即

Hess[19]认为流动从初始时刻到进入准自相似阶段的时间尺度与h和流体声速之比具有相同的量级。同时考虑到热层左侧流场也应达到均衡状态,本文中选取流动进入准自相似阶段的时间为

式中:cR为波R 后流场声速,N为常数。至此,根据上一小节的理论方法计算固壁附近波T 强度,联立式(6)~(10)即可求解点P4附近的流场参量。
2 结果与讨论
2.1 MaI=2.00,0.1≤ρtl/ρair≤0.9 时的计算结果
给定波I 马赫数MaI=2.00,波前流场压力p0=0.100 MPa,空气密度ρair=1.00 kg/m3,热层高度h=0.50 m,空气和热层气体比热比均取γ=1.40。计算区域0<x<15.00 m 和0<y<10.00 m,热层左侧界面位于x=2.00 m 处。设定九种不同的工况,即热层气体密度ρtl分别取0.10、0.20、0.30、0.40、0.50、0.60、0.70、0.80、0.90 kg/m3,利用本文理论方法计算固壁附近流场参量。
同时,利用动力学软件ANSYS Autodyn Euler-FCT 求解器进行数值模拟。图6 所示为三种工况条件下相应时刻压力p和水平速度u沿固壁分布的数值模拟结果,Grid 1 和Grid 2 分别表示不同的网格划分方案,即dx=dy=0.01 m 和dx=dy=0.02 m,dx和dy分别为沿x和y方向的网格尺寸。两种网格方案所得到的结果基本吻合,验证了网格收敛性,后续的数值模拟均选用Grid 1。

图6 不同工况条件下压力p 和水平速度u 沿固壁的分布Fig.6 Profiles of pressure and horizontal velocity along the wall in different cases
2.1.1 流场中的激波结构
将DP1>DI和DP1<DI时流场中的激波结构(见图2~3)分别记为W1 和W2。两者的区别主要体现为,界面上方流场中的激波结构分别为五波和三波结构。表1 为不同工况条件下,t<h/cT时刻热层内波T 相关参数的理论计算结果,pT、pT′分别为波T 以及点P1附近波T′后的压力。对于MaI=2.00,当ρtl=0.87 kg/m3时,DP1=DI=748.33 m/s。图7 为t=0.5 ms 时刻压力等值线图的数值模拟结果,等值线间隔取为Δp=(pmax−pmin)/20,pmax、pmin为对应工况和时刻的压力最大值和最小值。此时,波R1未到达固壁。
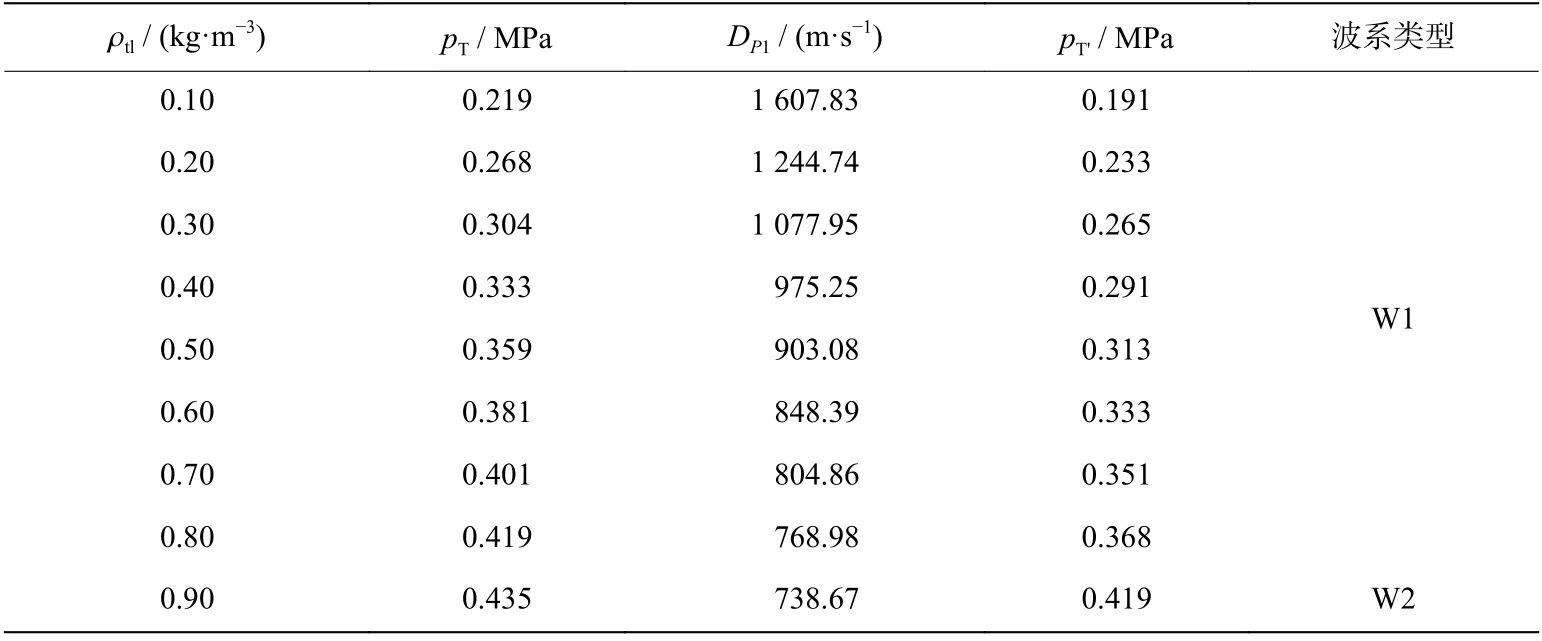
表1 流场中激波结构类型Table 1 Wave structure types above material interface
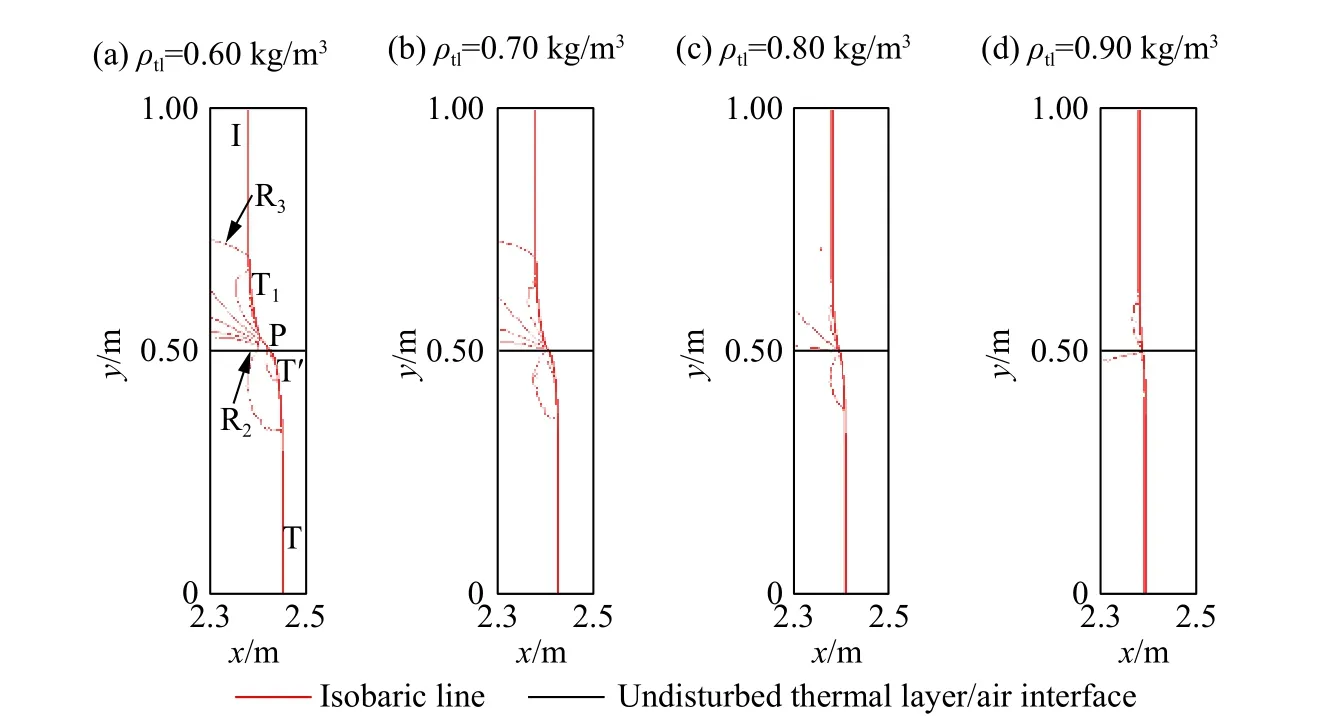
图7 t=0.5 ms,不同工况下的压力等值线图Fig.7 Pressure contour lines at t =0.5 ms in different cases
当ρtl≤0.60 kg/m3时,界面上方为五波结构,理论计算结果与数值模拟结果基本吻合。受到波后流场中扰动的影响,波R2、R3和T1后的流场区域并不均匀。当ρtl=0.70 kg/m3和0.80 kg/m3时,理论计算结果显示界面上方为五波结构,而在数值模拟结果中并未明显观测到波R2。这是因为两种工况处于波系类型由W1 向W2 的过渡区附近,根据理论方法得到的两种工况中波R2马赫数MaR2分别为1.20 和1.16,强度较弱。也可能是由于理论方法采用激波动力学理论近似描述波T 阵面弯曲,所得到的DP1略大于真实值,此时波系类型实为W2,理论计算结果与数值模拟结果存在偏差。
当ρtl=0.90 kg/m3时,界面上方的波系为三波结构,理论计算结果与数值模拟结果基本一致。波P 阵面略向前弯曲,理论计算得到波R4马赫数MaR4=1.02,接近声波。
2.1.2 固壁附近流场参量
选取工况ρtl=0.50 kg/m3,阐释固壁附近流场特征及参量的演化。图8 为t=13.0 ms 时刻流场密度云图的数值模拟结果。空气和热层气体经过激波压缩后,被卷入流场后方的涡旋中。随着时间发展,波T 传播距离大于14h,流动进入准自相似阶段。图9 为t=10.0、12.0、14.0 和16.0 ms 时刻固壁附近压力p和密度ρ 分布的数值模拟结果。热层左侧的流场,近似恢复到波I 后的状态,这与本文理论方法关于图5 中区域1 的假定是一致的。点P4、P5附近的压力和密度随时间基本不变。在时间间隔Δt=2.0 ms 内,波T 的位移分别为1.61、1.65 和1.62 m,也随时间基本不变。
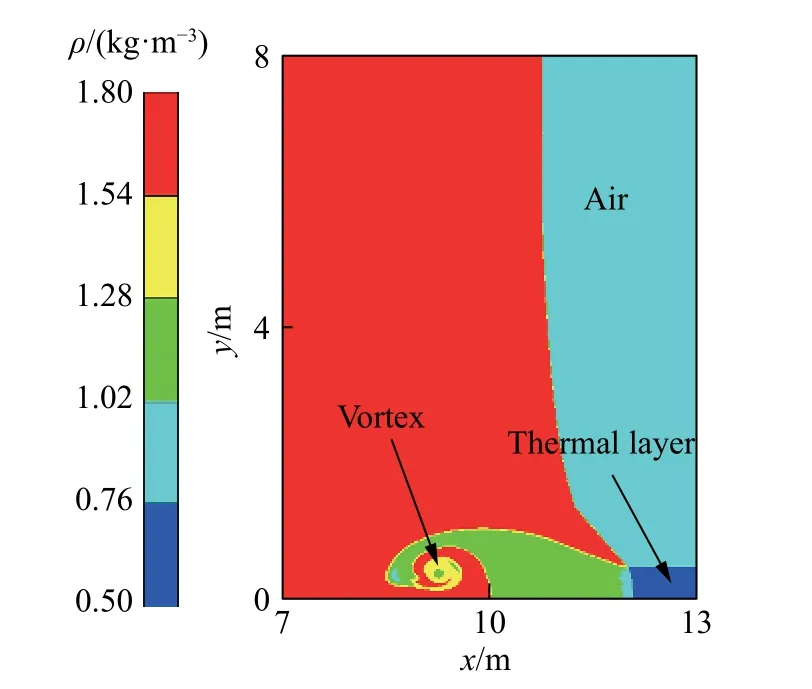
图8 t=13.0 ms,流场密度云图分布(ρtl=0.50 kg/m3)Fig.8 Density contour at t=13.0 ms with ρtl=0.50 kg/m3
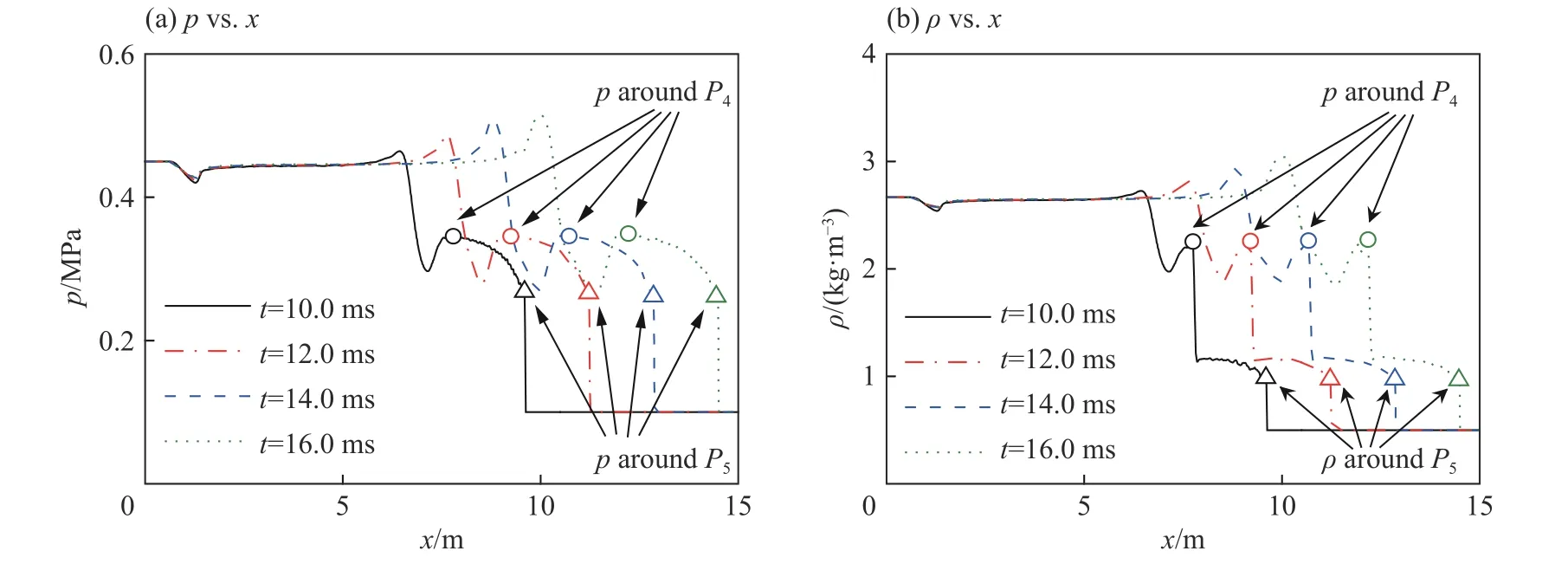
图9 不同时刻,物理量沿固壁分布(ρtl=0.50 kg/m3)Fig.9 Parameters vs. x along the wall at different time instants with ρtl=0.50 kg/m3
接下来,利用本文的理论方法,对不同工况下流场进入准相似阶段后点P4、P5附近的流场参量进行计算。其中,流场进入自相似阶段的时刻按式(11)计算,并取N=2.5,假定波T 后稀疏波以波T 后流场声速在热层内往返传播。表2 为不同工况下物理量p4、u4、ρ4L、ρ4R和p5的理论计算结果与数值模拟结果,其中,TA 表示理论计算结果,NS 表示数值模拟结果,ε=|TA-NS|/NS 为理论结果与数值模拟结果的偏差,t*为数值模拟结果的取值时刻。t*的确定应保证物理量趋近于渐近值,本文采用“在时间间隔Δt=0.5 ms 内物理量ρ4L数值变化不超过2%”作为判断标准。
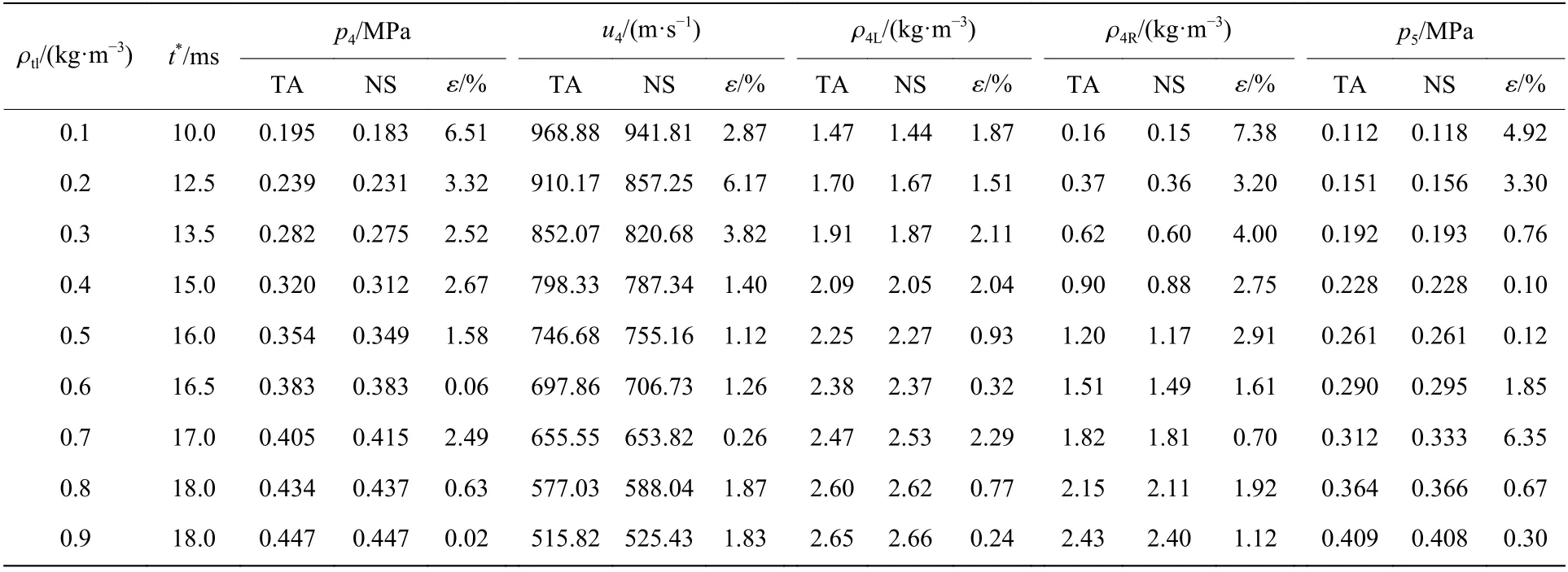
表2 不同工况条件下固壁附近流场参量Table 2 Parameter values near the rigid wall for different cases
当热层不存在时,波I 后固壁附近流场的压力为0.450 MPa。热层的出现,使得固壁附近激波峰值压力降低,且峰值压力随ρtl减小而减小。对于不同的工况条件,流场参量的理论计算结果与数值模拟结果的偏差均小于10%,验证了理论方法的合理性。
2.2 与Shreffler 和Mirels 理论方法的比较
选取与上一小节相同的工况参数,分别利用Shreffler[7]理论方法和Mirels[20]理论方法对固壁附近流场参量p4、u4和p5进行计算,并与本文理论计算结果进行比较,见图10。在Shreffler 理论方法中,前驱波阵面与水平方向的夹角α 根据sin2α=ρtl/ρair确定,该式的计算结果已被证实与实验数据较为吻合[3,11]。在Mirels 理论方法中,速度比例系数k(k=u4L/u4R)描述的是点P4附近界面两侧速度之比,且0<k≤1.0。k值依赖于具体的工况条件,Mirels 根据其理论计算结果与实验数据或数值模拟结果是否吻合来确定k值,但并没有给出k与工况条件的具体关系。此处,初步选取k=1.0,0.3,0.01 进行计算,以涵盖k可能的取值范围。
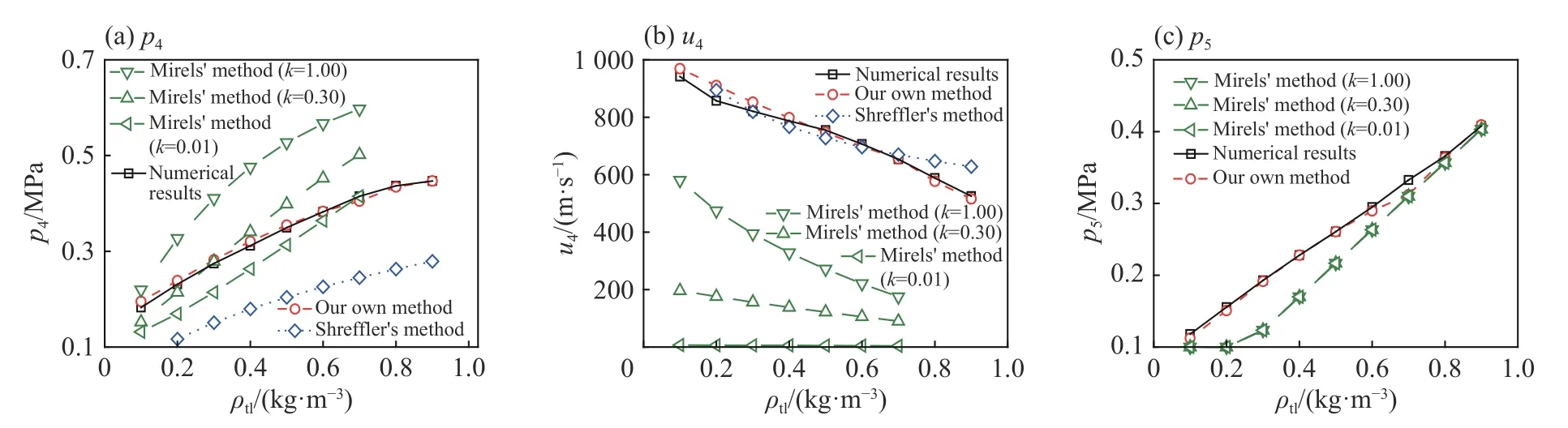
图10 不同理论方法的计算结果(MaI=2.00)Fig.10 Results from various theoretical methods with MaI=2.00
从图10 可以发现,Shreffler 理论方法仅能给出p4和u4,其中p4的结果与数值模拟结果偏差较大,u4的结果则与数值模拟结果较为接近。Mirels 理论方法给出的p4与数值模拟结果的偏差大小与k值有关,当k=0.3 时,ρth≈0.28 kg/m3的结果与数值模拟结果最接近,当k=0.01 时,ρth≈0.70 kg/m3的结果与数值模拟结果最接近;对于任意的k值,u4的结果均与数值模拟结果存在较大偏差;随着ρtl/ρair趋近于1,p5的结果与数值模拟结果偏差逐渐减小。本文理论方法所给出的p4、u4和p5,与数值模拟结果偏差均小于10%,表明本文理论方法在此类工况条件下优于Shreffler 理论方法和Mirels 理论方法。
2.3 Zaslavskii 实验
Zaslavskii[14]利用氮气与氢气的混合气体构建热层,在激波管中开展了MaI=1.36 的竖直平面激波与水平热层作用实验,并测量了不同 ρtl/ρair(ρtl/ρair<0.5)条件下波T 沿固壁走过约12h后的强度ξT=pT/p0,按照2.1 节所采用的准则判断,流动进入准自相似阶段。Zaslavskii 并未详细给出流场初始状态参数p0、ρair等,但由于ξT是一个无量纲量且不依赖于p0、ρair等物理量的具体数值,因此本文在开展理论计算和数值模拟时,不失一般性,取p0=0.101 MPa、ρair=1.225 kg/m3、γ=1.4,且N=2.5。图11 给出了ρtl/ρair=0.1、0.2、0.3、0.4 和0.5 时波T 强度ξT和固壁附近p4、u4的理论计算结果和数值模拟结果,并与Zaslavskii 测量得到的ξT进行比较。
对于MaI=1.36 和ρtl/ρair≤0.5,由于入射激波速度小于热层内气体声速,Shreffler 理论方法和Mirels 理论方法均不再适用,因此图11 中仅列出了本文理论方法的计算结果。图11(a)为波T 强度ξT,对于不同的ρtl/ρair,数值模拟结果与实验结果基本吻合,理论计算结果与数值模拟结果最大偏差约8.60%。图11(b)、(c)分别为点P4附近的流场压力p4和速度u4,理论计算结果与数值模拟结果较为吻合,其中p4对应的最大偏差为13.8%,u4对应的最大偏差为20.6%,随着ρtl/ρair增大,偏差逐渐减小。

图11 不同理论方法的计算结果(MaI=1.36)Fig.11 Results from various theoretical methods with MaI=1.36
3 结 论
当竖直平面激波与固壁附近水平热层作用时,流场中会出现涡旋和前驱波等结构。为了更为准确地计算流动处于准自相似阶段时固壁附近的流场参量,本文对已有的Mirels[20]理论方法进行了以下三个方面的改进:
(1)舍弃“热层内激波速度与入射激波速度相等”的假定,基于激波动力学理论计算热层内激波与波后稀疏波作用;
(2)在与入射激波后流体而非入射激波阵面固连的坐标系中,入射激波后流体在定常等熵波作用下,形成沿固壁运动的“活塞”;
(3)不再引入速度比例系数,而是假定“活塞”内流体与其毗邻的热层气体,满足压力和速度连续。
设定不同的工况,利用本文中改进后的理论方法计算固壁附近流场参量,并与数值模拟结果、已有的实验数据以及Shreffler 理论方法和Mirels 理论方法的计算结果进行对比。给定入射激波马赫数2.00 和热层与空气密度之比0.10≤ρtl/ρair≤0.90,对于热层上界面处扰动未到达固壁之前的流场激波类型,本文理论方法与数值模拟所给出的结果基本一致,但由于激波动力学理论自身存在一定近似,因此在激波类型发生转变的区域附近,理论计算结果与数值模拟结果还存在一定的偏差;当流动进入准自相似阶段后,本文理论方法得到的热层内激波强度以及物质界面两侧流场压力、速度和密度等流场参量,与数值模拟结果偏差均小于10%,明显优于Shreffler 理论方法和Mirels 理论方法。
给定入射激波马赫数1.36 和热层与空气密度之比0.10≤ρtl/ρair≤0.50,由于此时入射激波速度小于热层内气体声速,Shreffler 理论方法和Mirels 理论方法不再适用,而本文的理论方法依然可以应用;本文理论计算得到的热层内激波强度,与数值模拟结果和已有的实验数据较为吻合,与数值模拟结果最大偏差约8.60%,物质界面处流场压力、速度的理论计算结果与数值模拟结果最大偏差约20%。
通过以上对比可以发现,与现有的Shreffler 和Mirels 理论方法相比,本文的计算结果与数值模拟结果和已有的实验数据更为吻合,且其适用范围也更为广泛。本文的研究结果可加深对激波与热层作用机理的认识,为建立斜面或球面激波与热层作用流场的理论计算方法提供参考。

