基于公平性最优的大型医用设备配置规划方案

王 婧 李鹏伟

大型医用设备是指使用技术复杂、资金投入量大、运行成本高、对医疗费用影响大且纳入目录管理的大型医疗器械[1]。大型医用设备配置管理目录分为甲、乙两类，其中甲类是指资金投入巨大，使用费用很高，技术要求特别严格的大型医疗设备，包括质子和重离子放射治疗系统及高端放射治疗系统等；乙类是指资金投入大、运行成本和使用费用高，技术要求严格的大型医疗设备，包括64排及以上X射线计算机断层扫描(X-ray computed tomography，CT)、1.5 T及以上核磁共振(magnetic resonance，MR)、X射线正电子发射断层扫描仪(positron emission tomography/computed tomography，PET/CT)、直线加速器等[2-3]。由于大型医用设备具有使用技术复杂、资金投入量大等特点，为保障人民群众健康，遏制医疗机构盲目购置的趋势，国家卫生管理部门对大型医用设备进行配置管理。通过对各省市大型医用设备进行配置规划，使大型医用设备的增长得到控制，从而控制医疗费用过快增长，并且使得医疗设备更安全有效地服务于人民群众。

如何进行大型医用设备配置规划，已有文献[4-6]提出不同的规划方法，这些文献均基于需求法，即综合考虑人均GDP、人口密度、床位数及每百万人口检查量等因素，根据本省市已有数据，预测未来数年各地区不同设备的需求量；这些文献均提出了较客观的规划方案，但未对所提方案进行效果评价。由于所提方案着重关注满足需求，可能使得经济和技术发达区域得到更多配置，而经济和技术相对落后区域所得配置愈来愈少，造成区域之间的不平衡甚至两极分化，因此未能达到逐渐缩小地区差异的宏观调控作用。对规划方案的评价，多数文献[7-10]从公平性角度入手，分别从人口公平性和地理公平性等方面进行评价，在满足基本需求的基础上，公平性越高，规划方案越好。然而，这些文献只对已有规划进行评价，并未给出详细的规划方案修改意见，使得决策者在进行各区域配置数量调整时，仍无客观可靠的理论支撑。基于此，本研究针对规划时未考虑公平性评价指标，规划评价后未给出量化修改建议等问题，提出基于公平性评价指标最优的优化方法，使得公平性最优这一指标在规划发布前就融入到规划方案中，从事后评价转化为事前考量，从公平性最优角度，为决策者提供规划制定的理论依据，供方案调整时参考，使规划方案能缩小区域间差异，保证区域间平衡发展。

1 公平性最优研究背景知识

1.1 优化问题

优化问题是通过数学建模，以各影响因素为自变量，将需要优化的事物设为目标函数，通过数学求解，得到使目标函数达到最优的自变量的取值[11]。根据目标函数的数目，优化问题可分为单目标优化(即只有1个目标函数)和多目标优化(具有多个目标函数)。典型的优化问题数学模型计算为公式1[11]:

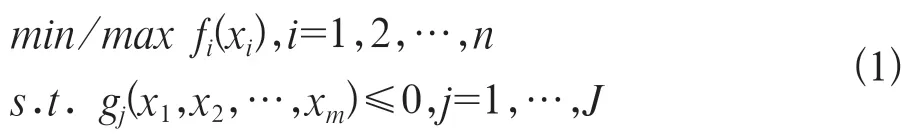
式中s.t.为“subject to”缩写，表示“在……约束条件之下”；fi为需要优化的目标函数，可以是1个(即单目标优化问题)，也可以是多个(即多目标优化问题)；max为最大化目标函数值；min为最小化目标函数值；xi为影响目标函数值的自变量；gj为约束条件。

根据实际问题，优化目标可以是最大化某个目标函数值(max)，或最小化目标函数值(min)。自变量(xi)是影响目标函数值的因素，gj是优化问题需要满足的约束条件(即限制条件)。通过求解优化问题，可以得到使得目标函数(fi)值最优(即最大或最小)的自变量(xi)的取值，即最优解。

求解优化问题的方法有多种，如遗传算法[11]、蚁群算法[12]等。本研究采用广泛应用的遗传算法，该算法模拟了生物进化规律，具体是指将自变量看成基因进行编码，在每一次迭代过程中，通过基因变异、交叉等操作，产生新的自变量的值，保留使目标函数值更优的基因，经过多次迭代，直到目标函数达到最优。

1.2 人口公平性

评价大型医用设备配置规划公平性，多数文献从人口和地理公平性两方面入手。对人口公平性，现有文献常选择基尼系数[13]作为评价指标，即根据各省市大型医用设备拥有量，计算大型医用设备基于人口分布的基尼系数[14-15]。基尼系数是由意大利经济学家基尼提出，用于定量描述社会平均分配程度，其值介于0～1，越接近0，表示资源分配公平性越高[13]。参照国际惯例，将基尼系数值0.4作为警戒线，若基尼系数值≤0.2，则认为设备分配绝对公平；基尼系数在0.2～0.3，为比较公平；基尼系统在0.3～0.4，则公平性一般；若基尼系数＞0.4，则表示公平性不佳，且越接近1，公平性越差[9]。基尼系数(G)的计算为公式2:

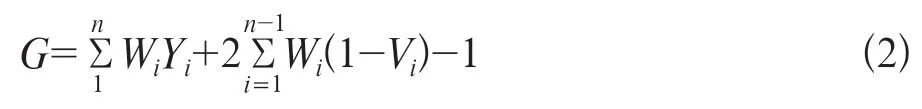
式中G为基尼系数；Wi为各省区市人口数占总人口的比重，Yi为各省区市大型医用设备的拥有量占大型医用设备总量的比重，Vi为Yi从i=1到i的累计数，i为各省区市大型医用设备拥有量从低到高的排序，n为省区市的总数。

2 公平性最优研究方法

本研究以人口公平性最优为目标，以我国东部、中部及西部地区每百万人口设备拥有量差距为约束条件，以各省在规划年限内大型医用设备的增量为自变量，进行数学建模，其优化模型的计算为公式3:

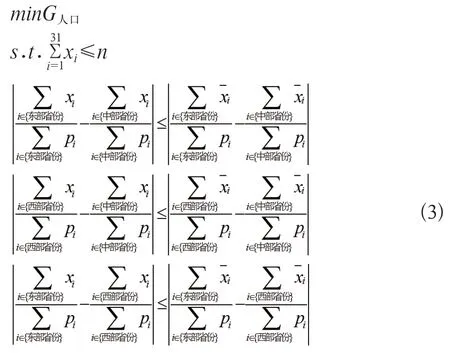
式中minG人口为优化的目标函数，即最小化基于人口的基尼系数；s.t.代表优化目标函数必须满足的约束条件，包括:①公式3第2行，表示各省新增大型医用设备数量之和≤全国规划总量；②公式3第3行，表示优化后的方案中，东部、中部和西部之间每百万人口大型医用设备拥有量的差距≤现有方案；xi为各省规划年限内大型医用设备增量，由于统计的是东部、中部和西部31个省区市，i从1取到31；n代表规划年限内全国大型医用设备增加总量。

优化目标为最小化基于人口的基尼系数G人口，其计算见公式2。因基尼系数愈小代表资源分布公平性愈高，因此目标函数最小化基于人口分布的基尼系数，即提高大型医用设备基于全国人口分布的公平性。除人口公平性，本研究优化问题同时考量了地理公平性，并将地理公平性指标作为约束条件。由于全国各省区市有效居住面积与实际面积不同，故本研究优化问题选用全国东部、中部及西部每百万人口差距作为地理指标，选取现有东部、中部及西部每百万人口设备拥有量差距为约束值，尽量缩小东部、中部及西部每百万人口设备拥有量差距，提高大型医用设备基于地理因素的分布公平性。根据《中国卫生和计划生育统计年鉴2016》，东部地区包括北京、天津、河北、山东、江苏、浙江、福建、上海、辽宁、广东和海南11个省市，中部地区包括河南、安徽、湖北、湖南、江西、山西、黑龙江和吉林8个省，西部地区包括陕西、甘肃、青海、宁夏、新疆、四川、云南、重庆、贵州、广西、内蒙古和西藏12个省区市。

优化问题通过遗传算法，可找到各省设备增量x1，x2，…x31的一组最优取值，使得基于人口的基尼系数G人口最小，且东中西部每百万人口设备拥有量差距不超过现有差距值，达到人口和地理公平性的优化。

3 公平性最优研究应用

以大型医用设备中乙类设备CT和MR为例，应用本研究方法，得出使人口与地理分布公平性最高的规划方案。

根据国家卫生健康委员会《关于发布2018-2020年大型医用设备配置规划的通知》[16]中的2018-2020年大型医用设备配置规划，截止2018年本研究选取的31个省区市乙类设备中的CT和MR数量为4584台和5395台(表1)；2018-2020年间规划新增总量分别为CT≤3535台，MR≤4451台。根据本研究方法，可以得到基于人口和地理公平性最优的规划方案，见表2。

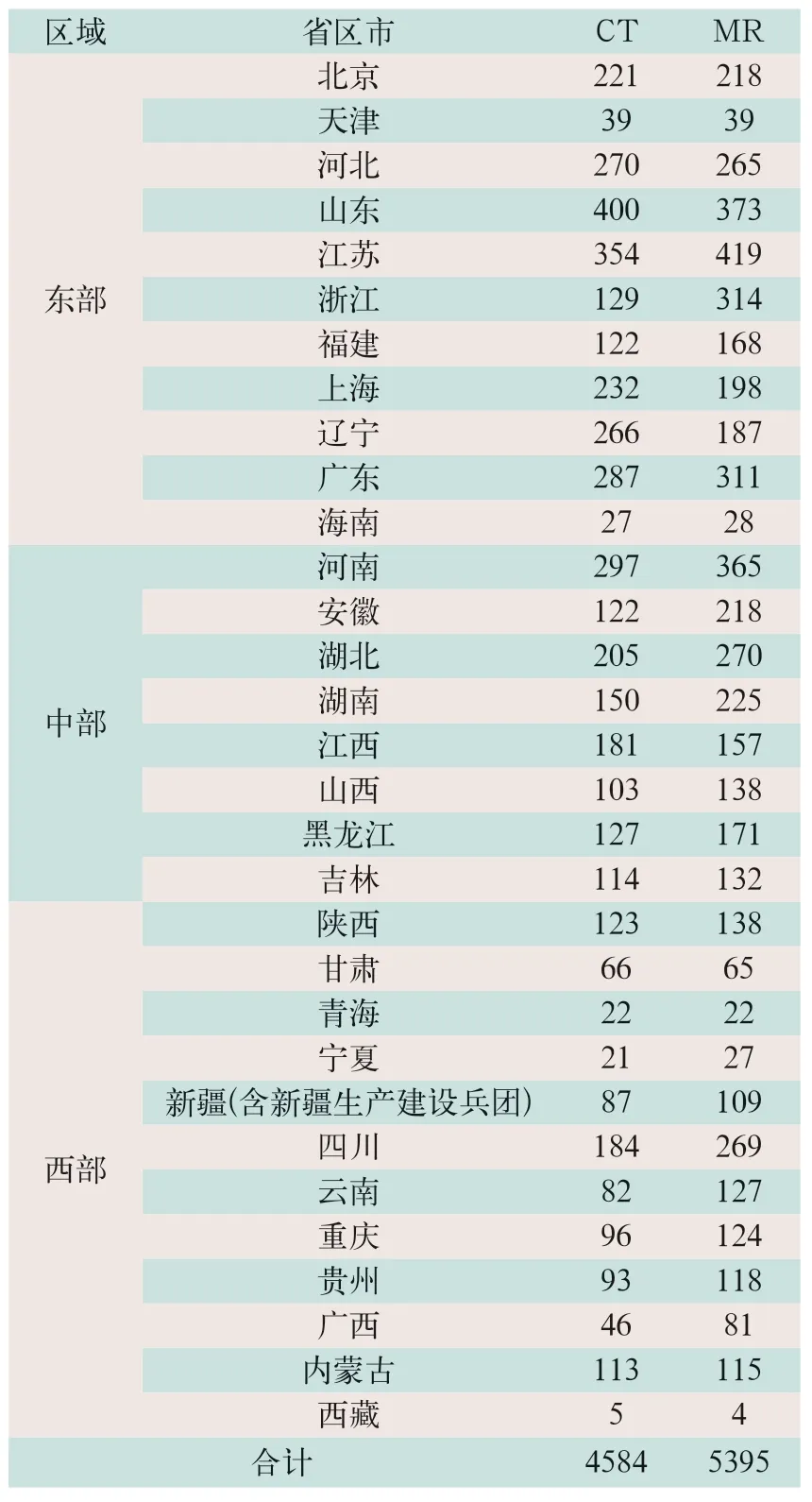
表1 截止2018年31个省区市现有CT和MR数量(台)

表2显示，现有规划方案中，CT和MR的基于人口公平性的基尼系数分别为0.16和0.13；优化方案中，CT和MR的基于人口公平性的基尼系数分别为0.12和0.10，CT和MR现有方案与优化方案的基尼系数见图1和见图2。

图1和图2显示，CT和MR现有的规划方案在人口公平性上均达到了很高标准；优化方案基于人口公平性的基尼系数较现有方案均有所降低，表明优化方案的人口公平性较现有方案有所提高。

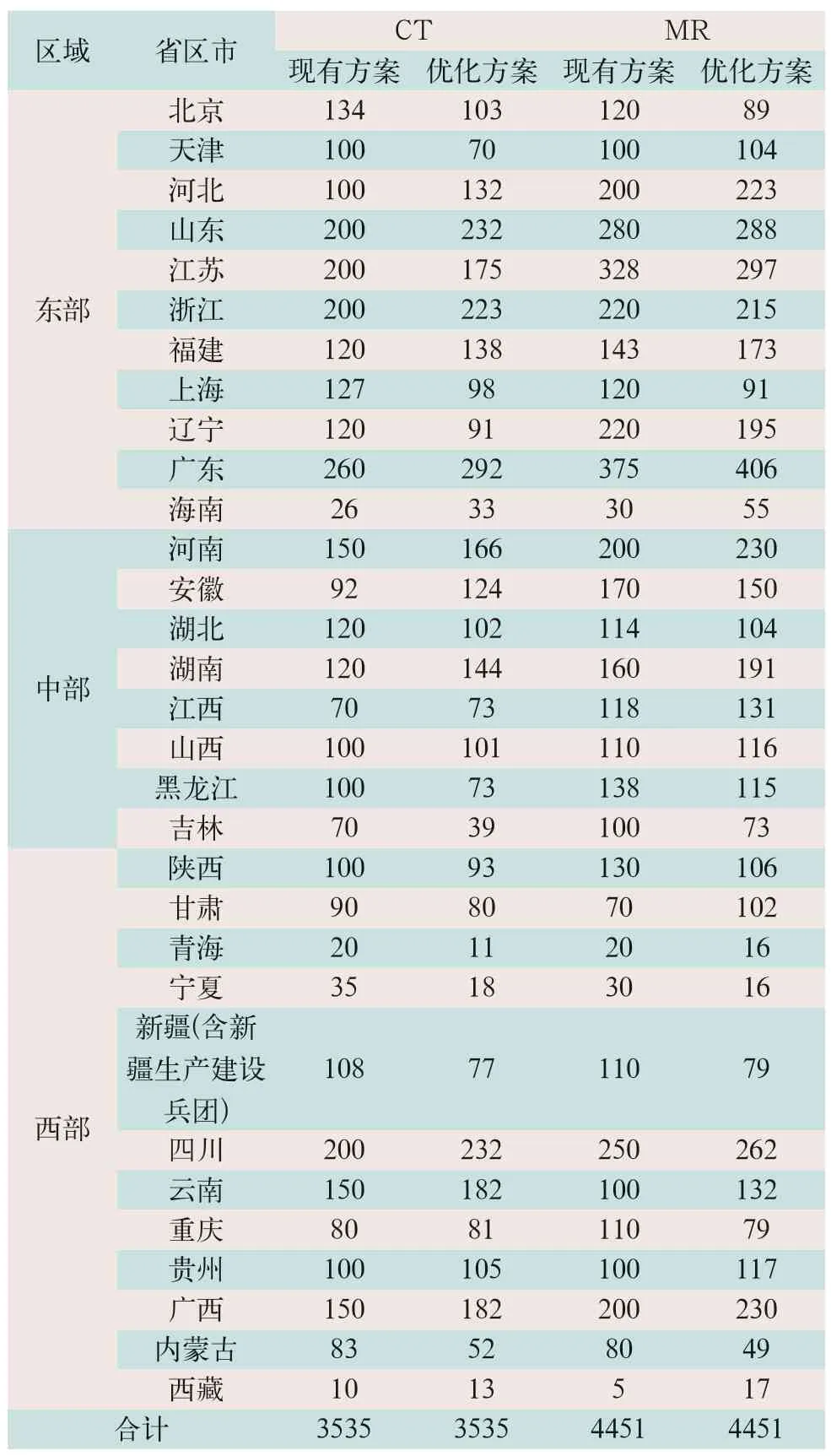
表2 现有方案与优化方案中CT和MR增量(台)

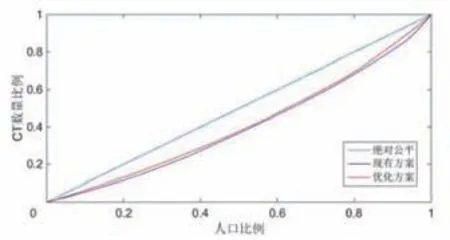
图1 CT现有方案与优化方案的基尼系数

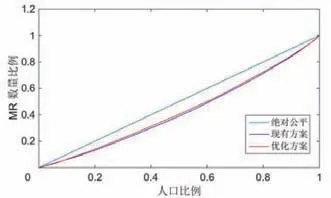
图2 MR现有方案与优化方案的基尼系数

东部、中部及西部每百万人口设备拥有量差异可根据表2计算得到。对比现有方案和优化方案的东部、中部及西部每百万人口设备拥有量差距，可以得出，现有方案和优化方案中，东部与中部每百万人口CT拥有量差距均为1.99台，中部与西部每百万人口CT拥有量差距均为0.63台；同样，MR在现有方案和优化方案中，东部与中部每百万人口设备拥有量差距均为1.71台，中部与西部每百万人口设备拥有量差距均为0.003台。结果显示，现有方案和优化方案对东部、中部及西部每百万人口拥有量保持一致，表明优化方案较现有方案，在保持地理公平性一致的情况下，提高了人口公平性，从总体上使得方案公平性有所提高。

4 结语

配置规划的公平性是衡量规划方案优劣的重要指标之一，但目前对规划方案公平性的评价往往是事后评价，决策者进行规划时往往未能使公平性达到最优的理论依据，且对规划草案调整时又缺少量化的修改建议。因此，本研究提出的基于公平性最优的配置方案优化方法，可使公平性最优这一指标在规划制定过程中就被融入到规划方案中，为决策者提供方案调整的理论依据和参考。本研究下步将细化优化问题，加强地理公平性优化程度，综合考虑更多影响因素，如各省区市的肿瘤发病率、设备利用率、有效居住面积等，使优化方案更加精细。