单次放射治疗时间管理模型的研究

艾 念 杜泽天 汪文靖 徐业成 罗 文

随着放射治疗系统的提升，现代精确放射治疗日趋人性化和智能化。然而，在治疗过程中，由于不同技师操作习惯、操作速度及摆位技术能力等因素影响，会导致不同的放射治疗技师对患者的治疗时间有所差异，且每班2名技师的配班组合也对治疗时间存在一定的影响[1]。因此，对单次放射治疗时间管理模型研究，将有利于做出更合理的工作安排与治疗预约排程，为工作效率评价提供量化参考指标，对患者治疗质量和治疗效率有重要意义[2-3]。

1 单次放射治疗时间管理模型研究资料与方法

1.1 研究资料

选取武汉科技大学附属孝感医院同一时间段接受放射治疗的10例患者，将其编号为P1至P10，统计其治疗时间，并由5名放射治疗技师记录其摆位时间。

1.2 时间模型建立方法

解析影响放射治疗时间的患者状况、技师配班和治疗参数3个主要因素，分别建立时间管理模型算法[4]。

1.2.1 准备时间模型

患者状况包括姓名、年龄、性别、病情及治疗前准备，从治疗前准备时间量纲在模糊评价模型的理论基础上创建患者治疗前准备时间模型，不探究单独某个因素对结果的影响方式，而是讨论患者的所有因素对行动时间总的影响[5]。通过模型得到评价结果后，再将其向时间量转换，得到患者行动时间。

1.2.2 预计摆位时间

不同技师配班，从摆位时间量纲采用移动平均法，对已有技师组合进行分析，通过采用不同的移动项数，得到多组预测值，选取其中方差最小的结果作为该组技师的摆位预测时间[6]。通过MATLAB软件进行矩阵运算，得出技师预计的摆位时间[7]。

1.2.3 确定最终模型

根据患者计划的总剂量、主射野数和子野数，从治疗时间量纲利用Eviews软件对包括机器跳数、子野数在内的剂量因素进行最小二乘法拟合，得出多元回归模型，再通过假设检验确定最终模型[8]。

1.2.4 制作程序界面

利用MATLAB软件的图形用户界面(graphical user interface，GUI)做出程序界面，将模型嵌入程序内，得到更加简单直观的程序界面[9]。通过该单次治疗时间模型预测患者治疗时间，对放射治疗进行优化排程，从而使放射治疗过程中的时间达到最优。

2 单次放射治疗时间管理模型研究结果

2.1 患者治疗前准备对时间影响

患者治疗前准备时间是受多种因素影响的一项综合结果，本研究从患者年龄、性别、病情和治疗前准备4个指标，建立患者治疗前时间影响体系，见图1。

图1 患者治疗前时间影响因素

将上述4个重要评价指标作为评价对象的因素论，U={u1，u2，u3，u4}。通过已经确定的患者编号，将10例患者构成目标矩阵，A={A1，A2，A3，…，A10}，得到了一个10行、4列的决策矩阵P，见表1。

表1 10行4列决策矩阵

对每一个评价指标，均建立一个等级集合v={v1，v2，v3，v4，}，每一个等级可对应一个模糊子集，表示为4、3、2、1，每个子集有4个元素，每个元素将会通过影响时间的程度确定。通过以上得出的决策矩阵和评估等级集合，对每个因素pi,j做出评价，确定模糊综合评价矩阵R，其中矩阵元素通过上述求出的关系矩阵和权重值，得到下述对患者配合程度的评价模型，其计算为公式1:

式中Q为配合程度的评价矩阵，P为决策矩阵，R为模糊综合评价矩阵。

通过不同患者不同评价指标的评价指数可以确定评价模型结果，将结果规定以便向时间量纲转换，模型关系是经已有数据进行最小二乘法拟合得到，其计算为公式2:

式中TA为拟合矩阵，Q为配合程度的评价矩阵。

根据公式2计算得出相关系数0.8795，表明该因素时间拟合情况良好。

2.2 不同配班技师摆位对时间影响

不同配班放射治疗技师的摆位时间与技师摆位操作工作习惯流程有相关性，且不同技师配班对摆位时间也存在差异。

放射治疗技师的摆位时间是受主观因素影响较大的一个量，通过一段时间对技师摆位时间的记录不难发现其时间数值随机性较大，难以发现其趋势，主要是因为不同放射治疗技师的工作习惯有一定差异性，包括技师的移动速度、摆位处理方式和操作机器的速度等，而即便对于同一位放射治疗技师，其摆位时间也会受到诸多因素的影响而产生差异。

选取医院5位放射治疗技师，分别编号为A、B、C、D和E，记录其摆位时间，采用移动平均法对不同技师组合的摆位时间进行预测，将各技师组合下的观测值联合得到方程组，最终确定每位技师的摆位时间。

设观测序列为y1，…，yT，取移动平均的项数N＜T，一次简单移动平均值计算为公式3:

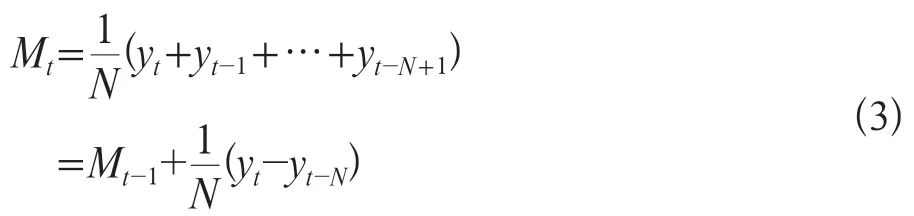
式中Mt为移动平均值，N为移动平均项数，y为观测序列。

预测目标的基本趋势是在某一水平上下波动，则可用一次简单移动平均方法建立预测模型，其计算为公式4:

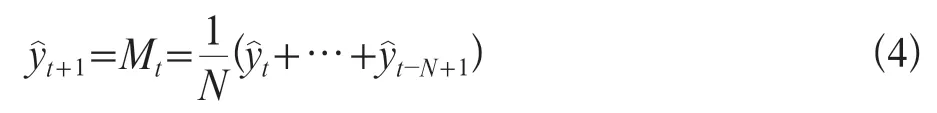
式中Mt为移动平均值，N为移动平均的项数，y为观测序列。

预测标准差计算为公式5:

式中S为预测标准差，T为平均总项数，N为移动平均项数，y为观测序列。

该标准差表征技师摆位时间的误差岐离[11]。

2.3 机器跳数和射野数对时间影响

由于加速器的剂量率一定，故机器跳数与患者的治疗时间呈现正相关关系。静态调强过程中，加速器在每个机架角度的射野里包含若干治疗子野，子野的数量与治疗时间也成正相关性。

患者的靶区平均剂量、主野数和子野数均应与治疗时间成正线性相关，所建立的计算模型为公式6:

式中TD为相关系数，X1～X3为相关参量，A、B、C和D为参量系数。

其回归方程计算为公式7:

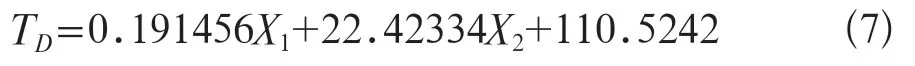
式中TD为相关系数，X1和X2为相关参量。

在拟合优度上，经自由度修正的相关系数为0.978025，可见模型整体拟合较好。F检验，针对原假设，H0∶A=B=C=0，给定显著性水平α=0.05，由于回归系数的P值即理论t值超越样本t值，得概率分别为0.034、1.16×10-6、0.0413和方程整体的P值6.53×10-7均＜α，故应拒绝原假设H0∶A=B=C=0，回归方程显著，即患者治疗的机器跳数和子野数对患者的治疗时间有显著影响[12]。t检验，同样对于给定显著性水平α=0.05，回归系数的检验值分别为t=2.628314，t=15.41972，t=2.4 955460；P＞2.35，故在95%的置信度下拒绝原假设H0∶A=B=C=0，自变量对回归方程影响显著。

由置信区间计算公式(M-n×ST，M+n×ST)给出下面置信区间(α=0.05时，n=1.96)，统计每例患者单次治疗时间，见表2。

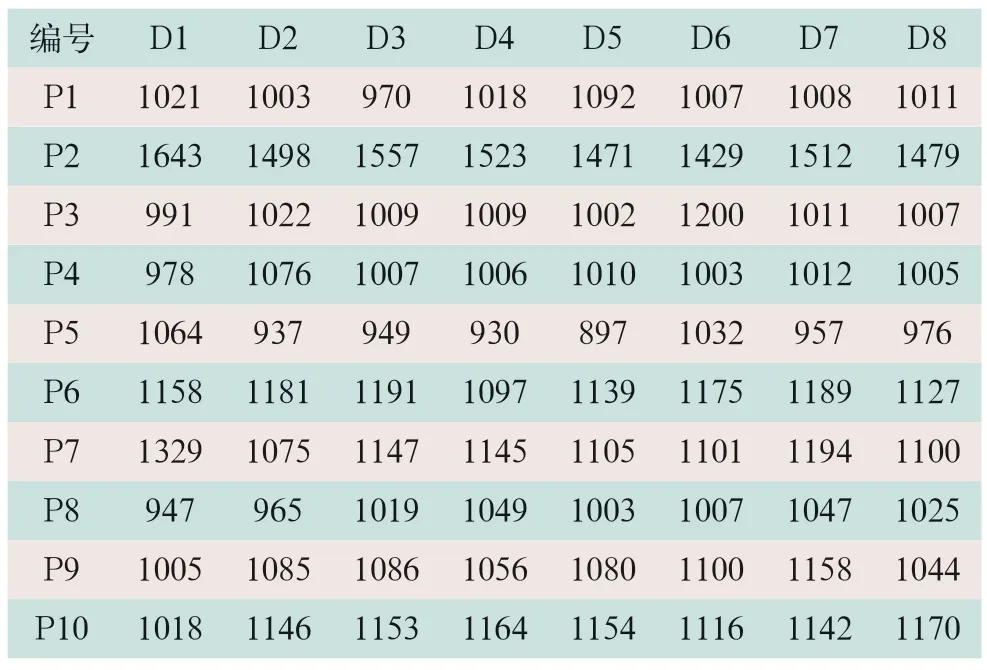
表2 每例患者单次放射治疗时间统计(s)

利用MATLAB软件对上述单次治疗时间解析后进行GUI设计，将已有的数学模型通过GUI简单选择，为了尽可能地使操作界面简单化，编写程序时使技师或物理师在使用软件时尽可能地减少键盘输入次数而用鼠标进行选择，故针对患者年龄、性别、病情、退衣程度以及放射治疗技师的组合选择、是否转床等均采用GUI中的弹出式菜单供使用者进行直观简便地选择目标参数，对于像机器跳数和子野数这种无法以有限的组合来表示的量则采用手动输入方式进行参数输入，这样仅需数步简便操作即可快速得到针对目标患者的放射治疗时间预测[13]。GUI运行界面见图2。

图2 患者放射治疗时间GUI

3 讨论

本研究将患者单次放射治疗时间模型分解为多个相对而言便于计算的小模型，减少了计算量的同时也使模型条理更加清晰明确。

3.1 患者行动时间模型

患者行动时间模型中，创新地使用了基于模糊评价原理做出的患者配合度综合评价模型，影响患者行动时间的所有因素均是共同影响的最终结果，该方法能够不考虑具体哪个因素是如何影响结果的，而是对所有因素进行评价，使其共同决定结果，最终得到目标模型。

3.2 技师摆位时间模型

技师摆位时间模型中，涉及到摆位是技师之间两两合作对患者进行摆位，采用了移动平均法对下一次的摆位时间进行预测，相对于直接求出平均数，移动平均法能有效避免因随机因素所引起的计算误差，通过改变平滑项数可获得多组观测值，再通过寻求最小方差得到最终的最优结果。

3.3 剂量—时间模型

在剂量—时间模型中，运用经典的多元回归分析Eviews软件进行分析，通过分析把无效变量替换和删除后的模型符合定性分析和定量分析。Eviews软件能把回归分析的相关数据全部显示在结果中，便于观察之外更加方便后续的模型检验，进一步减少工作量。

做出满足要求的模型后，得到的模型加入到MATLAB软件的GUI中，使复杂计算的算式变成直观简单的程序界面，使放射治疗技师或物理师在使用相关模型时更加方便，极大减少了模型的使用难度。

3.4 模型的建立

在模型的建立上，患者配合度综合评价体系中，其评价指标的各项权重是靠放射治疗技师的经验得出，具有一定针对性。放射治疗技师摆位时间的预测中，各技师组合所观测的次数不尽相同，在进行方阵选择的时候不同的方阵会得出不同的结果，由于技师是2人同时摆位，因此对单独技师的摆位预测在排班时基本不会考虑，这是导致出现时间误差岐离的原因。

4 结语

本研究所进行的放射治疗患者时间分析，对患者放射治疗时间有着良好的优化意义，可为放射治疗预约排程和治疗效能分析提供量化参考。由于本研究包含数据量不够大，模型相对简化等问题，尚需对本研究所出现的模型进行优化，建模方法上也可引入人工智能算法进行优化，加上有足够的数据支持，相信能得出更优且更加符合医院情况的结果。