基于交叉口相位裕量时间的公交准点控制模型
卢 凯, 夏小龙, 胡建伟, 林永杰
(1.华南理工大学 土木与交通学院, 广东 广州 510640; 2.现代城市交通技术江苏高校协同创新中心, 江苏 南京 210096;3. 华南理工大学 亚热带建筑科学国家重点实验室, 广东 广州 510640)
公交车辆能否准点到站是城市居民决定是否选择公交出行的一个重要影响因素.研究发现,出行者在不同出行目的和有无换乘情况下的候车时间价值将大于换乘时间价值和运行时间价值[1],等候公交车时间已取代步行至公交车站的时间成为影响居民出行方式选择的主要因素[2].目前,由于公交车辆到站准点性较差,已经严重影响到了城市公交分担率[3].因此,如何提升公交车辆到站准点率是发展公交战略亟待解决的一个关键问题.
近年来,公交车辆到站时间预测与公交准点控制研究受到了国内外学者们的重视与关注,取得了不少研究成果.在国外,Cathey等[4]根据车辆定位数据与历史数据,利用卡尔曼滤波方法实现了对公交车辆到站时间的预测;Shalaby[5]则进一步建立了公交车辆路段行程时间和停站时间模型;Koushki与Paul等[6-7]提出了一种公交重点站服务模式,并基于车辆自动定位数据分析了重点站服务模式对保证行车准点率的影响.在国内,温惠英等[8]提出了基于灰色关联分析的路段行程时间实时预测算法;卢凯等[9]提出利用乘客乘车动态诱导方法,建立了一种公交车辆停站时间控制模型;周雪梅等[10]给出了公交站间准点率的一种定义,应用极值理论建立了公交站间准点率计算模型,并对相邻站及重点站间的公交运行准时性进行了评价;王菁[11]给出了以线路与站点为基础的准点率关系模型,研究了以站点为基础的公交运营相对及绝对准点率的相互关系.
然而,目前有关公交准点性研究主要还是集中在公交行程时间的可靠度分析方面,对于公交车辆在各站点间,特别是在信号交叉口的主动管控缺乏研究,因此如何建立交叉口信号配时方案与公交到站准点性能之间的相关关系,利用交叉口信号配时设计提高公交到站准点率值得进行深入分析研究.
1 原理分析
在图1中,r1为基于交叉口相位裕量时间(定义为车辆按计划运行抵达信号交叉口时的预期等待时间)控制的公交车辆计划运行时间位置轨迹线,T1、T2为公交车辆到达站点S1、S2的准点时刻,tP1、tP2为公交车辆到达站点S1、S2的准点允许时间范围,tM1、tM2、tM3为交叉口I1、I2、I3的相位裕量时间.针对公交车辆到达交叉口I1时间点的不同情况,分析各自行驶状况如下:
(1) 当实际行驶轨迹线如r2时,在交叉口I1,由于实际到达时刻位于相位裕量时间所在的同一红灯时间段内,故在绿灯启亮后轨迹线r2将回归计划运行轨迹线r1,从而保证后续到达站点S1、S2的准点性.
(2) 当实际行驶轨迹线如r3时,在交叉口I1,由于实际到达时刻位于相位裕量时间段内,故在绿灯启亮后轨迹线r3将回归计划运行轨迹线r1,从而保证后续到达站点S1、S2的准点性.
(3) 当实际行驶轨迹线如r4时,在交叉口I1,尽管实际到达时刻与计划到达时刻之间的偏差大于准点允许时间范围,但由于相位裕量时间的作用,实际离开时刻与计划离开时刻之间的偏差将调节至准点允许时间范围内,从而保证到达站点S1的准点性;在交叉口I2,由于实际到达时刻位于相位裕量时间段内,故可保证到达站点S2的准点性.
(4) 当实际行驶轨迹线如r5时,同样利用交叉口I1及交叉口I2的相位裕量时间,可将实际离开时刻与计划离开时刻之间的偏差逐步调小,从而保证到达站点S1、S2的准点性;在交叉口I3,由于实际到达时刻位于相位裕量时间段内,故可保证后续到站的准点性.
分析可见,交叉口相位裕量时间可以调控公交车辆实际离开时刻与计划离开时刻之间的偏差,通过一个或多个信号交叉口的逐步调控,可以使得公交车辆恢复准点运行.
2 模型方法
2.1 模型参数


图2 信号交叉口与公交站点布置情况
假若各交叉口的信号相位相序设计及绿信比分配方案固定,各交叉口执行公共信号周期以保证各班次公交车辆准点率控制效果的稳定.忽略信号交叉口初始排队车辆影响,选取任意相邻信号交叉口Ii和Ii+1进行公交准点率建模分析,如图3所示.
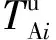
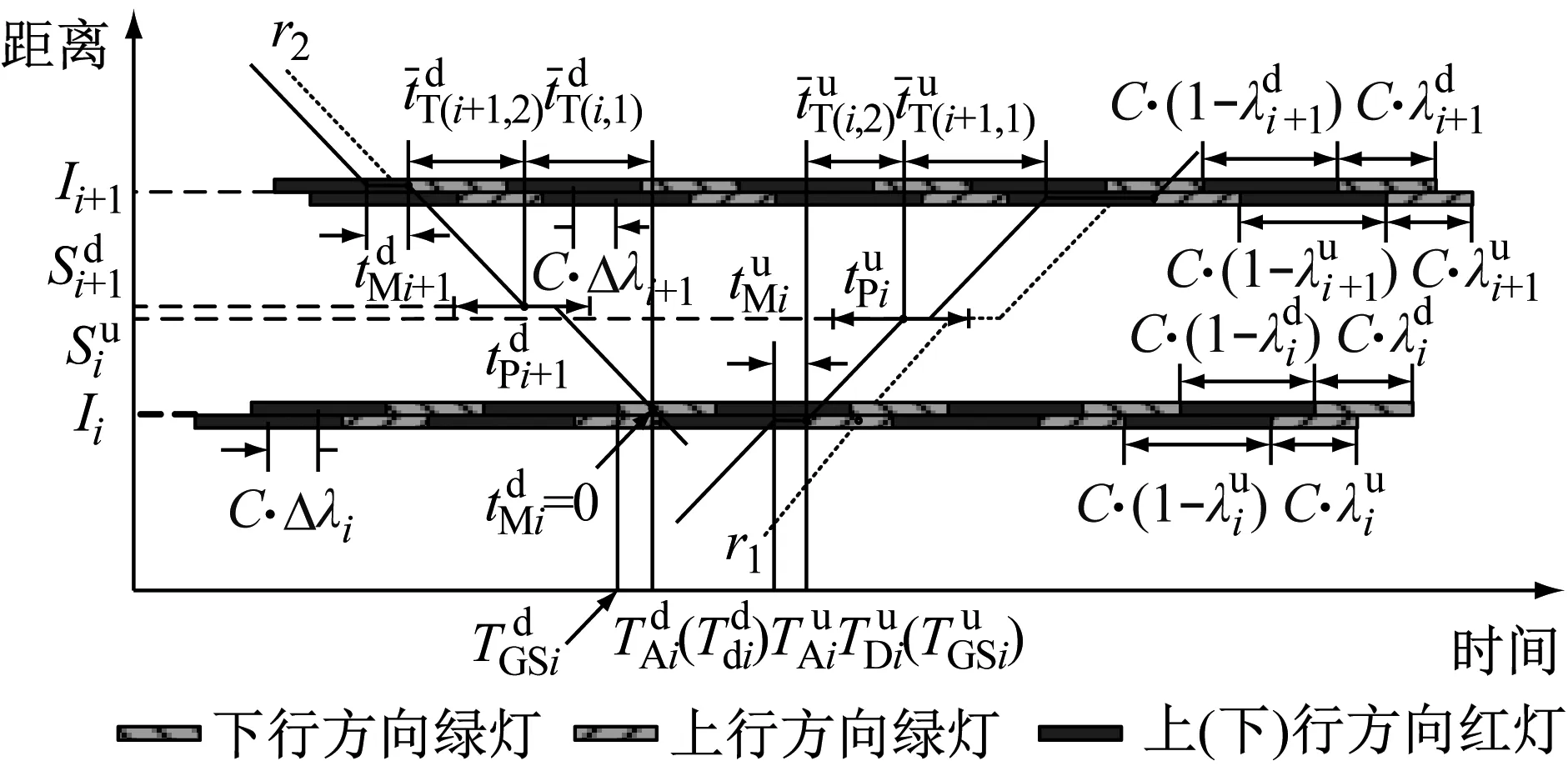
图3 公交准点控制时距分析图
2.2 到站时刻分析
2.2.1上行方向
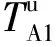
(1) 交叉口I1
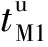

(1)
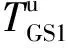
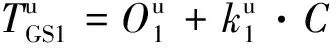
(2)
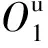
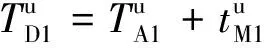
(3)

(4)
(2) 交叉口Ii(i≥2)
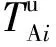
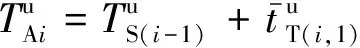
(5)


(6)

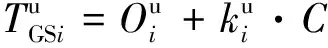
(7)

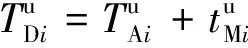
(8)
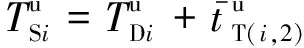
(9)
2.2.2下行方向
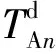
2.3 交叉口准点域
根据公交车辆到站准点允许时间范围的要求,可以反向推导上游交叉口准点域的计算方法.
(1) 准点域起始时刻
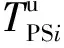
(10)
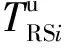
(11)
(2) 准点域结束时刻

(12)
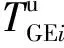
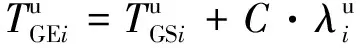
(13)
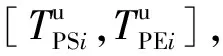
2.4 目标函数
当上游交叉口准点域范围越大,且其中心与计划到达时刻偏差越小,则越有利于提高公交车辆到达下游公交站点的准点性.因此定义整个公交准点率控制模型的优化目标函数P为
(14)
式中:αu与αd分别为上行与下行方向的准点性需求权重系数,通常设置αu+αd=1.
2.5 优化变量约束条件
(1) 公共信号周期
公共信号周期C的优化空间应满足:
C∈[Cmin,Cmax]
(15)
(2) 相位差

(16)
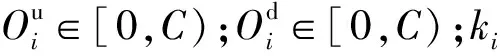
(3) 到达时刻
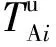
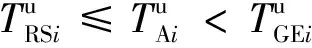
(17)
(18)
整合约束条件、目标函数以及优化变量取值空间关系式,可以建立公交准点控制模型.
3 算例分析
假设某公交线路沿线经过I1、I2、I3、I4共4个信号交叉口,交叉口I1至交叉口I4为上行方向,交叉口I4至交叉口I1为下行方向,公交站点的布置和节点间各路段的平均行程时间如图4所示.

图4 公交站点布置及各路段平均行程时间(单位:s)

表1 各交叉口信号配时基本参数
利用交互式的线性和通用优化求解器(linear interactive and general optimizer,LINGO)对本例模型进行编程求解,解得最佳公共信号周期为150 s,各交叉口上下行方向的相位差与相位裕量时间设置如表2所示,模型的目标函数优化值为74.
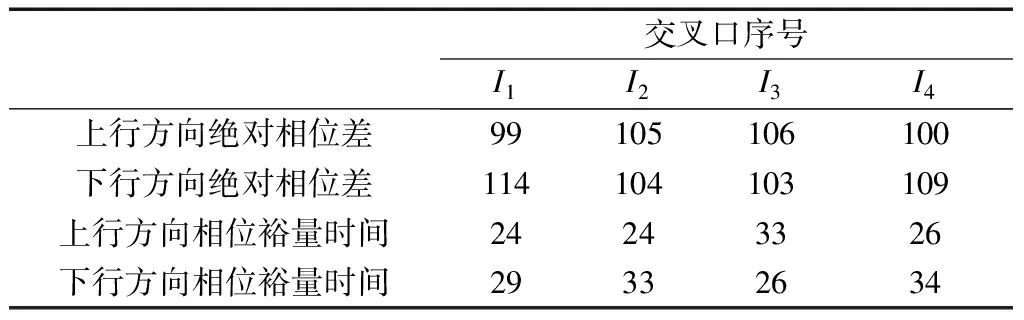
表2 公交准点最优控制方案
注:绝对相位差参照同一个基准点取值.
根据表2所示的公交准点最优控制方案,并结合已知公交车辆运行条件,绘制出相位裕量时间控制下的公交车辆计划运行时距图,如图5所示.
由图5可以看出,上下行方向各公交站点的上游交叉口准点域大小均接近于一个公共信号周期,达到了通常情况下的理论极限值,控制方案可以使得一定时间范围内的公交车辆均能在到站准点允许时间范围内抵达下游公交站点.
假定下行方向第一频次的公交车辆发车时刻为7:00:00,公交发车间隔取10 min.以上下行方向各2个频次的公交运行情况为例,根据公交准点最优控制方案可以确定公交车辆计划到站时刻表如表3所示.采用本文模型优化得到的公交准点控制方案,将能够最大程度地保证公交车辆在表3所示的计划到站时刻附近到达相应的公交站点.
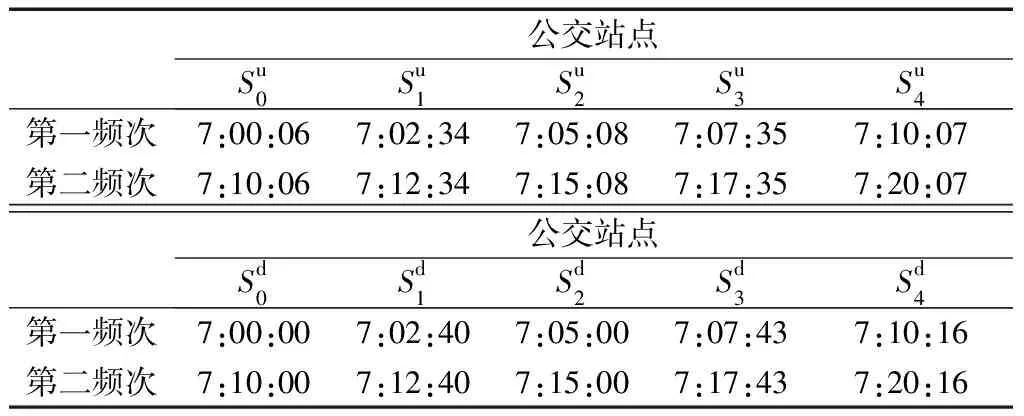
表3 公交车辆计划到站时刻表
4 仿真实验
假设公交车辆平均行驶速度为36 km·h-1,在速度区间[24,48] km·h-1内服从均匀分布;利用交通仿真软件VISSIM建立第3节算例的仿真路网模型.

图5 公交车辆计划运行时距图
Fig.5 Time-space diagram of bus traveling schedule
公交线路车辆的发车间隔时间设置为600仿真秒,通过在相应位置设置行程时间检测器,对公交车辆行程时间进行统计,仿真时长取999 999 s;运行得到公交车辆从始发站到达各站点的行程时间原始数据.对比公交到站准点范围,通过统计分析得到各公交站点的准点车辆数及准点率,具体结果如表4所示.
通过编程可以计算得到,在公交准点最优控制方案运行下,保证公交到站准点的最低与最高准点车速如表5所示.

表4 各公交站点的准点率

表5 各公交站点的准点车速范围
对比表4与表5可以看到,上、下行方向各站点的仿真准点率与理论准点率相差均在3%以内,考虑到条件设置误差以及VISSIM软件自身局限,由此验证了本文模型的可靠性,也说明本文模型对于公交准点率控制的有效性.
5 结语
本文针对公交准点控制需求,利用交叉口相位裕量时间,找到了交叉口信号配时设计与公交准点到站控制之间的结合点,建立了以上游信号交叉口准点域最大为控制目标的公交准点控制模型;通过优化干线交叉口的公共信号周期和相位差,得到了面向准点率控制的交叉口信号协调优化方案,提出了一种公交到站时刻表的制定方法;最后通过VISSIM仿真验证了模型的可靠性,为提升公交准点率提供了一种新的解决思路与方法.

