复杂抽样调查设计多值有序资料一水平多重Logistic回归分析
王 慧,李长平,2,胡良平
(1. 天津医科大学公共卫生学院卫生统计学教研室,天津 300070;2. 世界中医药学会联合会临床科研统计学专业委员会,北京 100029;3. 军事科学院研究生院,北京 100850
*通信作者:胡良平,E-mail:lphu812@sina.com)
调查资料,尤其是临床科研或试验资料,结果变量常为“疗效”(死亡、无效、好转、显效、治愈)或“效果”(优、良、中、差),此类资料被称为多值有序资料[1]。在获取此类资料的调查研究中,为提高样本对总体的代表性和估计的可靠性,研究者常将分层抽样、整群抽样、简单随机抽样组合使用,这种调查被称为复杂抽样调查设计。然而,在对复杂抽样数据进行回归分析时,研究者常常忽略此前采取的抽样设计方法。在不同的抽样阶段下,每个个体所对应的抽样概率不同,抽样权重也就不同,因此,抽样误差估计极为复杂。孙日扬等[2]认为,在复杂抽样调查研究的分析中应考虑抽样权重和观测权重,同时提出了综合权重的概念。在多重线性回归分析中纳入综合权重的分析结果更加准确、稳健。本研究通过不同的分析策略对复杂抽样调查设计多值有序资料进行多重logistic回归分析,并探讨各种分析方法之间的异同。
1 累积多重logistic回归模型的构建与求解
1.1 累积logistic回归模型
结果变量为多值有序变量的logistic回归模型又被称为累积logistic 回归模型,它是二值变量logistic回归模型的扩展[3],其回归模型见式(1):

其中y*表示观测现象的内在趋势,不能被直接测量;xk(k = 1,2,…,p)为p 个自变量,ε 为误差项。当结果变量有J 个可能的结局时,相应的取值为y=1、y=2、… 、y=J,即共有J-1 个分界点将各相邻类别分开,即:若y*≤μ1,则y=1;若μ1<y*≤μ2,则y=2;…;若y*≥μJ-1,则y=J。
给定x 值的累积概率可以按式(2)表示。其中1-P(y ≤j|x)即为P(y ≥j|x),这样就依次将J 个可能的结局合并成两个,从而进行一般的多重logistic 回归模型分析。
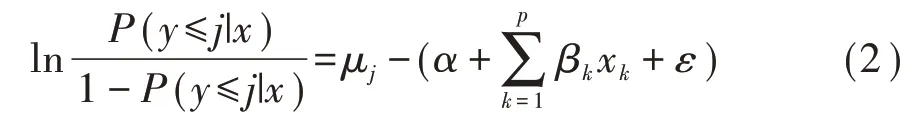
相应地,累积概率可通过式(3)进行预测:
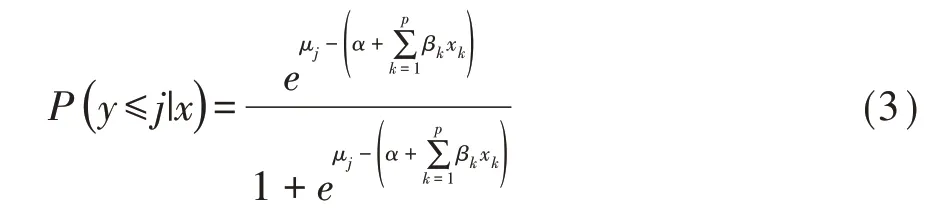
SAS 软件在实际运行中,定义β0j为各类中截距α与分界点μj的综合,所以上式就转化为式(4):
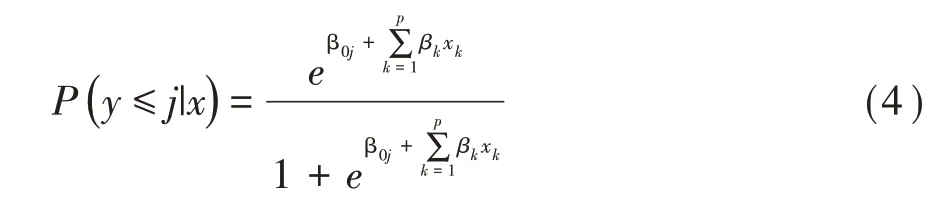
其参数估计采用最大似然法求解,其对数似然方程见式(5):
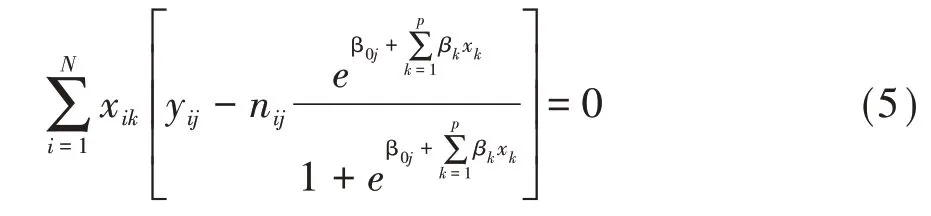
对式(5)的求解需要用到非线性迭代算法,一般需要借助统计软件来实现,此处从略。由以上讨论可知,如果结果变量中有J 个可能的结局,则可获得J-1 个累积logit 函数(当进行统计分析时,若有m 个截距项β0j无统计学意义,则只能获得J-m-1个累积logit 函数)。累积logistic 回归模型应用的假设条件是比例优势假定,其含义是自变量的作用与所有累积logit 的截断点无关,即对于任意一个自变量xk而言,所有的累积logit 都有一组相同的参数估计值,只是截距参数有所差别。若不满足比例优势假定条件时,Bender 等[4]建议可以考虑两种方法,一是采用独立的二分类模型,二是采用偏比例优势模型。
1.2 复杂抽样的多值有序logistic回归模型
复杂抽样多值有序资料的logistic 回归模型的构建、求解的思路和方法与单纯随机抽样设计资料的累积logistic 回归模型基本相同,主要差别在于:复杂抽样的多值有序logistic 回归模型考虑到了与特定抽样设计条件下对应的“抽样权重”[3]。其参数估计求解于下面的对数似然方程组,见式(6):

这种结合了抽样权重的似然估计通常被称为加权的最大似然估计或伪似然估计。
2 基于SAS的实例分析
2.1 问题与数据
本研究所使用数据为美国卫生与公众服务部开展的医疗支出调查(Medical Expenditure Panel Survey,MEPS),用于对医疗保健的各个方面进行全国性和地区性的评估。MEPS采用分层整群抽样,抽样权重会根据无响应情况进行调整,并根据当前人口调查的人口控制总量进行调整。在本例中,使用欧洲议会议员提供的1999年全年综合数据来研究家庭收入与性别和种族的关系。样本量为24 618,分层数为143,群集数为460。数据存储于SAS数据集MEPS。本例中变量命名及赋值见表1,分析所用示例数据见表2。

表1 MEPS数据集变量命名及赋值

表2 1999年美国家庭收入情况及影响因素数据(基于MEPS数据集)
2.2 分析策略
2.2.1 将复杂调查设计资料视为“单纯随机抽样设计资料”
2.2.1.1 SAS程序
需要调用LOGISTIC 过程来实现单纯随机抽样资料的累积logistic回归。【说明】“descending”选项要求对响应变量表中具有较低(1=贫穷)有序值的响应进行建模,class 语句指定分类变量sex 和race;model 语句中响应变量为income,解释变量(即自变量)为sex和race。在此段SAS 过程步程序之前,应基于表2 资料创建临时SAS数据集meps,此段SAS数据步程序省略了。
2.2.1.2 主要输出结果及解释
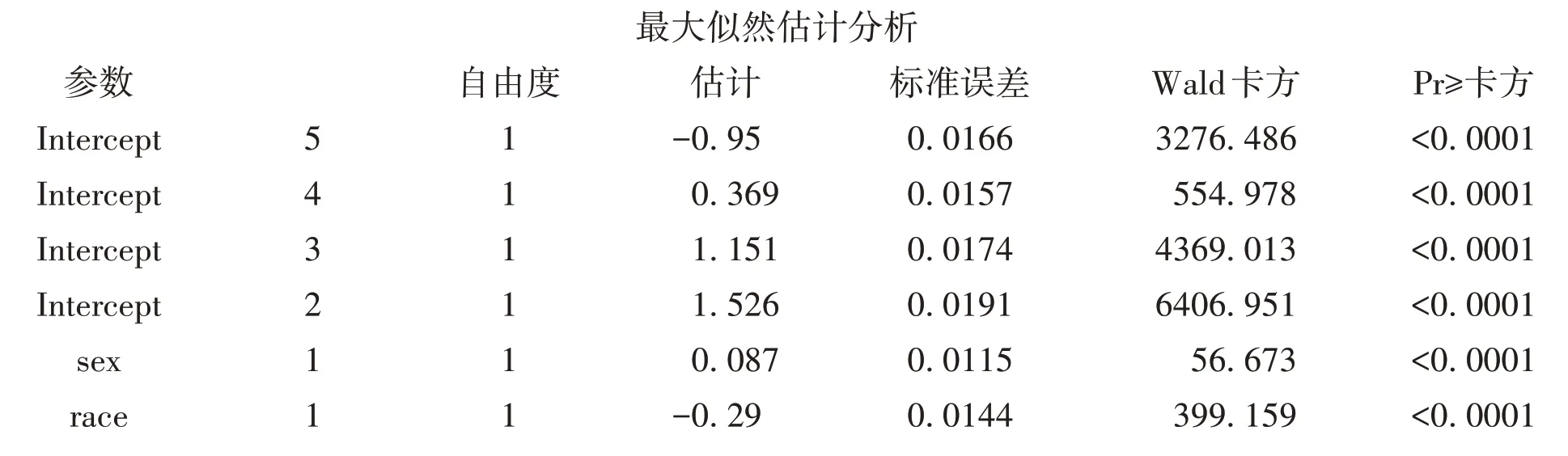

在形式上,累积logistic 回归模型分析的结果大致可分为模型基本信息、比例优势假定检验结果、模型拟合信息以及参数估计结果四部分。因篇幅所限,只给出参数估计结果;比例优势假定检验结果显示,χ2=7.4931,P=0.2766,不拒绝“比例优势假设”的条件,即满足比例优势假定,可采用累积logistic回归模型。拟合的累积logistic模型给出4个截距项以及sex和race的两个自变量的参数估计值,结果显示,性别和人种对家庭收入的影响均有统计学意义。女性贫穷的风险是男性的1.189倍;白种人贫穷的风险比其他人种低43.7%(=1-0.563)。
2.2.2 考虑抽样设计但不考虑抽样权重
2.2.2.1 SAS程序

需要调用surveylogistic 过程来实现复杂随机抽样多值有序资料的累积logistic回归模型分析:【说明】由于研究数据属于分层整群随机抽样调查资料,故在strata 语句中指定分层变量为stratum,cluster 语句中指定群集变量为cluster。
2.2.2.2 主要输出结果及解释
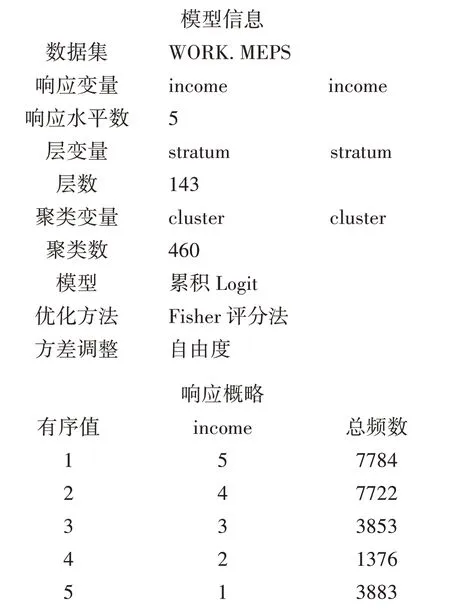
复杂抽样logistic回归主要结果大致可以分为三部分。第一部分是模型的基本信息,可以看到指定的分层变量和群集,拟合的是累积logistic回归模型;在响应概略表中可以看到因变量income顺序为5、4、3、2、1以及各响应水平的总频数。第二部分模型检验结果均显示整体模型具有统计学意义(P均<0.01)。


参数估计结果显示性别和人种对家庭收入的影响均具有统计学意义。女性贫穷的风险是男性的1.189 倍;白种人贫穷的风险比其他人种低43.7%(=1-0.563)。
2.2.3 考虑抽样权重,不考虑抽样设计
2.2.3.1 SAS程序
需要调用surveylogistic 过程来实现复杂随机抽样多值有序资料的累积logistic回归模型分析:

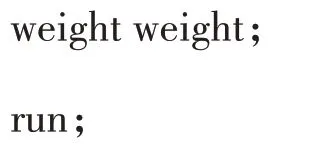
【说明】加入weight语句,指定权重变量weight。
2.2.3.2 主要输出结果及解释

与前文“模型信息”相同的部分此处从略。指定的权重变量在前文2.2.2.2的基础上增加的各响应水平的总权重。模型检验结果均显示整体模型具有统计学意义(P均<0.01)。
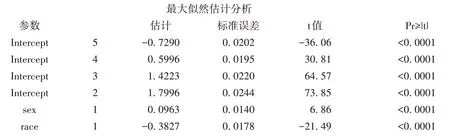
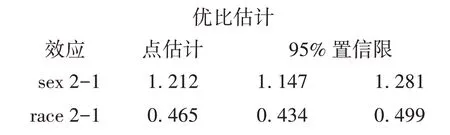
结果显示女性贫穷的风险是男性的1.212倍;白种人贫穷的风险比其他人种低53.5%(=1-0.465)。
2.2.4 同时考虑抽样设计和抽样权重
2.2.4.1 SAS程序
需调用SURVEYLOGISTIC 过程来实现复杂随机抽样多值有序资料的累积logistic回归模型分析:


【说明】在第“2.2.3.1SAS程序节”的基础上,加入strata语句指定分层变量stratum,加入cluster语句指定群集变量cluster。
2.2.4.2 主要输出结果及解释
与前文“模型信息”相同的部分此处从略。

模型的基本信息在“第2.2.3.2 主要输出结果及解释”的基础上增加了关于分层的内容。第二部分模型检验结果均显示模型总体具有统计学意义(P均<0.01)。


最后参数估计结果显示,女性贫穷的风险是男性的1.212 倍;白种人贫穷的风险比其他人种低53.5%(=1-0.465)。因此,最终建立的四个模型为:

2.3 不同分析策略的结果比较
结合上述分析结果可以看出,考虑抽样设计的累积logistic 回归模型与普通累积logistic 回归模型的结果相比,二者的参数估计值完全相同,但是sex的标准误降低且OR 值的置信区间缩窄,说明对分层整群抽样资料进行分析时,若忽视分层信息,则会导致过于保守的检验(P值偏大),同时OR 的置信区间也会变宽,容易出现假阳性结果;而race的标准误和OR 值的置信区间会增大,本研究认为主要是由于race在群内存在相关性导致的。
只考虑抽样权重的累积logistic 回归模型与普通累积logistic 回归模型的结果相比,参数估计值和标准误均发生了变化,sex的估计值和标准误变化不大,而在考虑抽样权重后race 的参数估计值降低,标准误和OR 值的置信区间几乎没有变化,所以本研究认为对于存在群内相关性的变量,在加入权重变量后,可在一定程度上校正这种群内相关性导致的预测不稳定。
同时考虑抽样设计和抽样权重的累积logistic回归模型与普通累积Logistic回归模型的结果相比,自变量的参数估计值和标准误均发生了变化,sex的估计值略高,而标准误和置信区间变化不大;race不仅标准误增大了,而且参数估计值也发生了变化,可能是因为race在群变量因素的各个水平中存在相关性,同时在该群变量水平的权重也很小,这也是为什么在考虑了抽样权重后,其标准误仅与考虑群变量的模型相比略有变化,因为它的影响很小。而同时考虑抽样设计和抽样权重的累积logistic 回归模型与只考虑抽样权重的累积logistic 回归模型相比,sex 的参数估计值不变,但其标准误降低、OR 值的置信区间变窄,说明在考虑抽样权重的基础上,纳入抽样设计的分析,会使分析结果更加准确和稳健。
3 讨论与小结
3.1 讨论
在社会科学或者卫生领域的研究中,尤其是大规模研究,常涉及多地区或者多中心的抽样,调查对象过于分散,若采用单纯的随机抽样,会出现调查成本高、可行性低的情况[5],所以研究者经常采用复杂抽样设计,以提高调查的可行性,节约调查的成本支出[6]。但在实际进行复杂抽样调查资料的统计分析时,多数研究者却常常忽略抽样设计,采用单纯随机抽样的普通logistic 回归模型分析。例如本研究数据是采用动态权重法进行的分层整群随机抽样数据,由于存在群变量,而有可能导致存在群内的相关性,若采用普通的累积logistic 回归模型分析,会导致较大的假阳性错误;其次,由于普通的累积logistic 回归模型的应用假设条件是所有样本均来自简单随机抽样,每一个个体被抽中的概率相同[7],所以不能将抽样权重纳入分析,也会造成信息的损失和结果的偏差。所以在对复杂抽样资料进行统计分析与推断时,将抽样设计和抽样权重正确纳入分析,是分析者应该重点关注的问题。
本文采用SAS 中的SURVEYLOGISTIC 过程对复杂随机抽样调查资料进行累积logistic 回归模型分析,这是一种基于复杂抽样调查设计的分析方法,可以结合抽样设计(分层、整群随机等)和抽样权重进行分析,可以不依赖于模型的假定,充分利用抽样权重、群效应信息等,进一步提高估计结果的准确性和稳定性[8]。考虑到本研究数据是分层整群抽样资料,这类资料也可以通过多水平logistic 回归模型进行分析,因篇幅所限,此处从略。
3.2 小结
本研究通过分层整群抽样的实例数据进行了不同分析策略的复杂抽样调查多值有序资料的多重logistic 回归分析,对分析结果给出了解释,并进一步探讨了不同分析策略结果之间的差异,结果表明:在对复杂抽样资料进行统计分析时,将抽样设计和抽样权重纳入分析,会得到更加准确和稳定的分析结果。

