非配对设计多值有序资料一水平多重Logistic回归分析

凤思苑，李长平，2，胡良平

（1. 天津医科大学公共卫生学院卫生统计学教研室，天津 300070；2. 世界中医药学会联合会临床科研统计学专业委员会，北京 100029；3. 军事科学院研究生院，北京 100850

*通信作者：胡良平，E-mail：lphu812@sina.com）

生物医学研究中最常见的问题之一就是探究各种影响因素（自变量X）与“是否发病”或“健康状况”（因变量Y）之间的关系。当结局变量是多值有序变量（如治疗结局为治愈、好转、显效和无效等）时，常用的线性回归模型就不再适合了。本文将结合实例介绍如何使用SAS实现非配对设计多值有序资料一水平多重logistic 回归分析，其中一水平主要是指受试对象不具有层级结构，即满足研究样本随机来自同一个总体（即认为受试对象在变量之间关系上具有“同质性”）。

1 基本概念

1.1 模型定义

多值有序logistic回归模型不同于二分类logistic回归模型，它是基于累积概率构建累积logistic 回归模型。假设结局变量Y有J个有序分类，其自然结局顺序表示为Y=1，2，…，J，每个分类结局对应的发生概率为π1，π2，…，πj，则其有序分类≤m的累计发生概率表示为P（Y≤m）=π1+π2+…+πm。因此，可以通过指定累积概率P（Y≤m）的阈值将整个结局变量Y的J个有序分类从指定的阈值点截断，使之成为二分类结局。设有P个自变量记为X=（x1，x2，…，xp）表示相应的影响因素。由此定义累积logit P（Y≤m）函数：

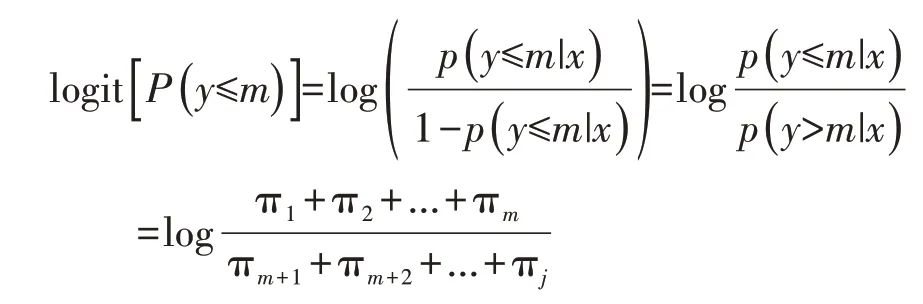
该累积logit P（Y≤m）函数是两个累积概率比的对数值，这两个累积概率分别表示结局变量Y 的取值小于等于结局分类m 与大于分类m 的可能性大小［1-2］。因为结果Y 共有J 个有序分类，故最多可以写成J-1个累积logit函数。

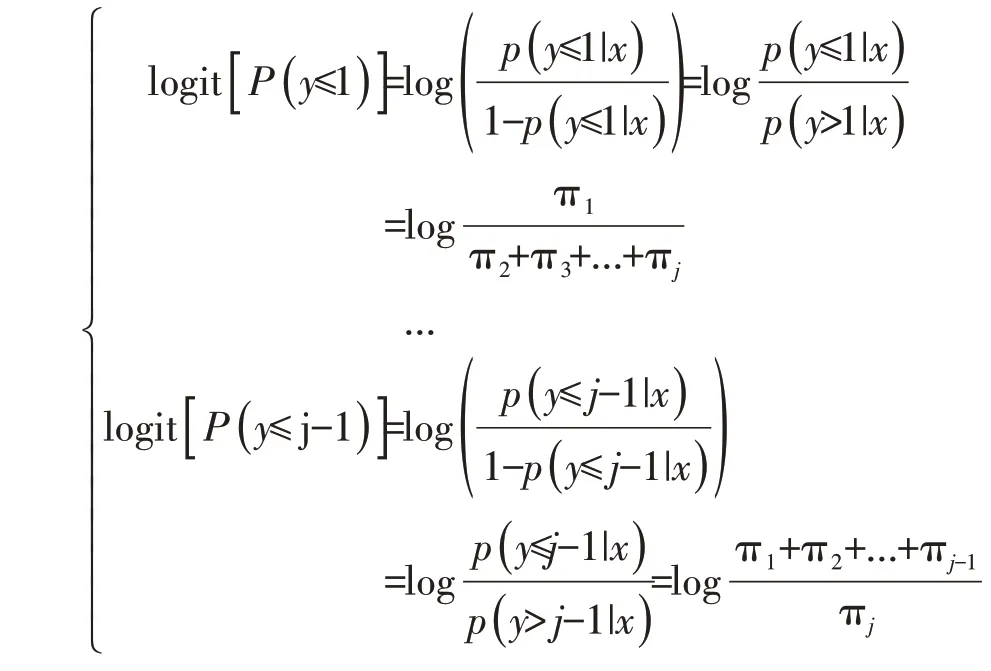
累积logit 函数还可以用线性函数形式表示如下：

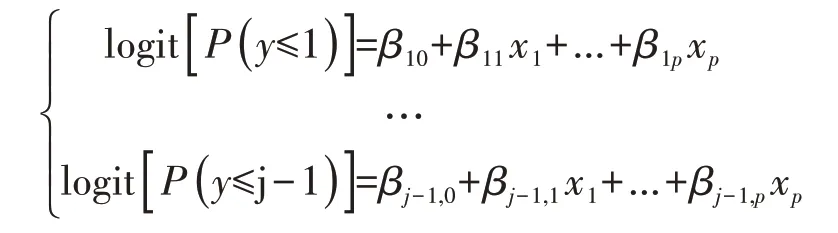
上述模型就是累积logistic 回归模型。为了进一步简化该模型，假定对于所有J-1 个累积logit 函数，各个自变量Xi所对应的系数βi假设都是等同的，即每个累积logit 函数相同自变量Xi都有相同的系数βi以及不同的截距βj0。在此假设条件下，J-1个累积logit 函数的回归线其实是相互平行的，只是截距βj0不同，该假设被称为平行假设。满足平行假设的模型简化后为：

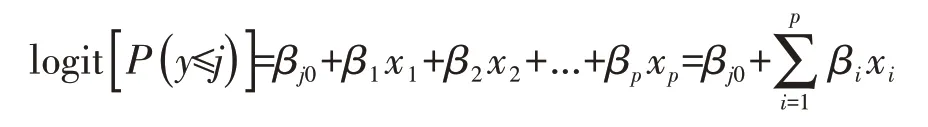
该简化后的模型称为成比例比数比累积logit回归模型，该模型和一般累积logistic回归模型一样，至多有J-1个方程形式，即同样有J-1个截距，但是p个自变量的回归系数在不同方程中分别相同［3］。该模型对应的概率模型形式为：通过上述公式，可获得结局Y取类别为j时的概率：

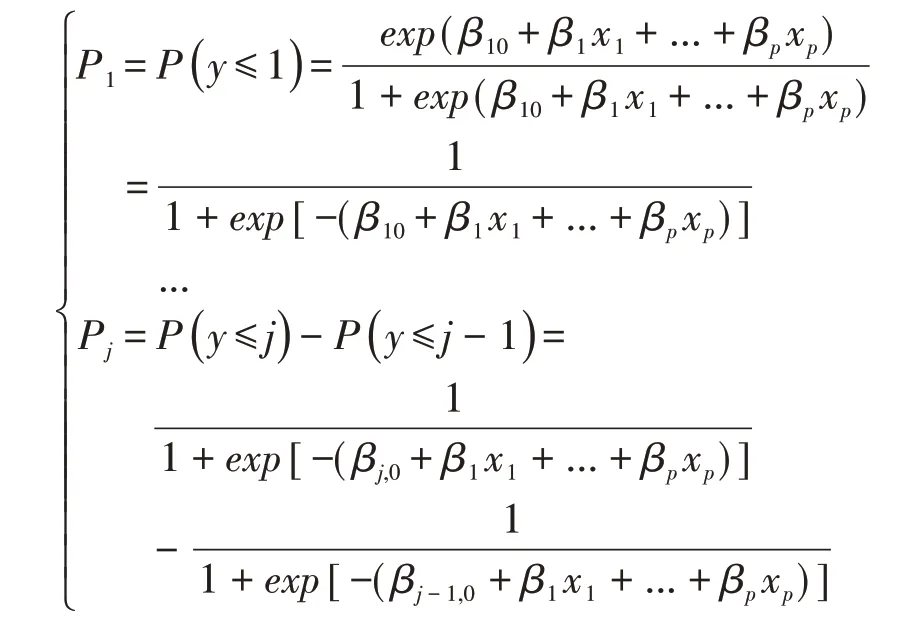
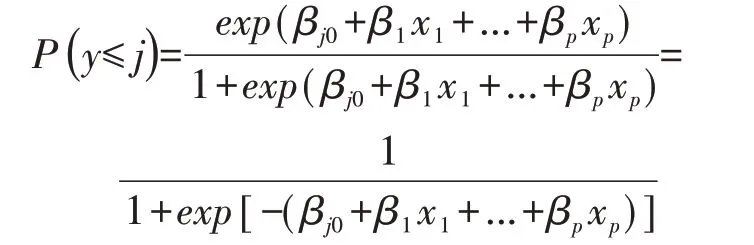
1.2 参数估计

多值有序资料的logistic 回归分析的参数估计和结局为二分类的logistic 回归分析相似，都可以用极大似然的方法估计［4］。对于n 个独立观察对象的样本，第i 个观察对象Xi出现Y=j 分类结局的概率记为Pj=P（Y=j | Xi），它是累积概率函数的差，即Pj=P（Y=j | Xi）= P（Y≤j | Xi）-P（Y≤j-1 | Xi）。由此构建的似然函数L为：

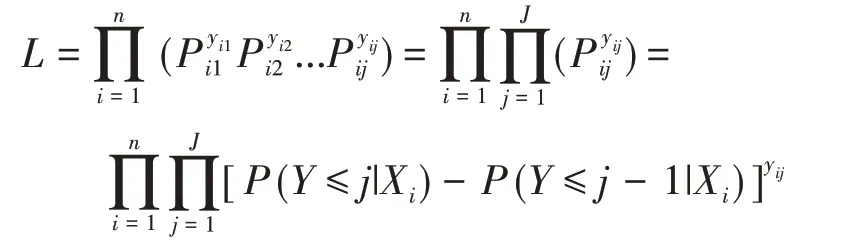
式中yij表示第i 个观察对象的结局变量Y 分类为j 等级时所对应的编码，它满足，而该观测实际只可能对应一个等级结局，故而只有某个yij取值为1，其余皆为0。相应的对数似然函数如下：

2 实例分析

冠状动脉旁路移植术（Coronary artery bypass grafting，CABG）是目前治疗冠心病最有效方法之一，但往往会存在术后静脉移植血管病变，从而降低血管通畅率并引起患者缺血症状的复发。为了研究引起术后血管狭窄可能的影响因素，随机选择207名CABG术后超过一年的患者，评价性别、桥龄、原位靶血管病变支数、冠心病类型、左室射血分数、左室舒张末期内径、α-羟丁酸脱氢酶、极低密度脂蛋白、脂蛋白a 和同型半胱氨酸对血管狭窄程度的影响。其中结局变量血管狭窄程度分为无狭窄（DS=1），部分狭窄（DS=2）和完全狭窄（DS=3）三个等级。见表1。

表1 多值有序logistic回归分析的数据表

2.1 SAS程序

【说明】首先建立临时数据集DS，依次输入变量性别、桥龄、原位靶血管病变支数、冠心病类型、左室射血分数、左室舒张末期内径、α_羟丁酸脱氢酶、极低密度脂蛋白、脂蛋白a 和同型半胱氨酸。接着调用LOGISTIC 过程完成累积回归模型的分析。其中class 语句为分类变量NLV 创建哑变量，选项ref=”3”是以变量的第三个水平为对照实现哑变量赋值；Model 语句中因变量为DS，其余变量为自变量。选项selection= stepwise 表示变量筛选采用逐步回归方法，选项sle 为选入自变量的显著性水平，选项sls 为剔除自变量的显著性水平。

接下来依次调用第二、第三个LOGISTIC 过程，采用的变量筛选分别为向前（forward）、向后（backward）回归方法。

【说明】在左栏的SAS 程序中，第2 和第3 个“model 语句”中省略号部分的内容与第1 个“model语句”中相应位置上的变量相同；在实际使用时，最好取“sls=0.05”。

2.2 结果解释

LOGISTIC 过程输出结果的第一部分为模型总体的相关信息，所分析的数据集是临时数据集DS，响应变量为血管狭窄程度DS，采用的模型方法为cumulative logit（累积logit），模型优化的技术为Fisher's scoring。结果变量共有三个水平，各自的例数分别为53、27 和117。其次该模型是以结局排序较低的取值为对比的基础，即以“y=1”为参照水平，也就是以血管无狭窄组为基础（即对照组）建模。

LOGISTIC 过程输出结果的第二部分输出了自变量筛选的过程，包括每次模型拟合后拟合统计量、整个模型检验以及平行线假设的结果。此实例中逐步法进行自变量的筛选过程共四步，由于篇幅原因，不做过多展示。逐步筛选法的筛选结果显示，最终自变量LVDED、HDT、LVN、QL 进入了回归方程。平行线假设的检验结果为χ2=9.4233，P=0.0933＞0.05，说明资料满足平行线假设。

LOGISTIC 过程输出结果的第三部分主要输出参数估计的结果：

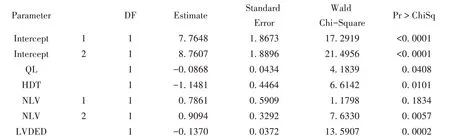
在累积logistic 回归模型中，截距项有多个，其个数为因变量的水平数减1。本例中因变量水平数为3，因此包含2 个截距项。如果用P1、P2、P3分别表示血管无狭窄、部分狭窄、完全狭窄的概率，则回归方程如下：

式中x1、x2、x31、x32和x4分别为自变量QL、HDT、NLV（1 VS 3）、NLV（2 vs 3）和LVDED。此外，本例中筛选出自变量对应的P 值均＜0.05，表明自变量的回归系数的估计值与0之间的差异均有统计学意义。其中QL 回归系数估计值小于0，说明自变量桥龄取值越大，血管出现无狭窄的概率P1越低，血管出现完全狭窄的概率P3越大。QL 的OR 估计值为0.917，95%置信区间为（0.844，0.996）。其他变量的结果：

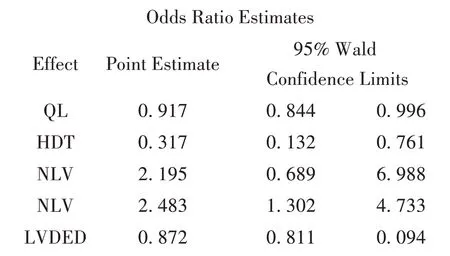
本文在筛选变量时除了逐步法以外，还采用了前进法和后退法。虽然变量筛选的具体过程不同，但最终纳入的变量以及相关的最大似然估计结果与逐步法相同，此处不做重复展示。

专业结论：桥龄（QL）、心脏病类型、原位靶血管病变支数和左室舒张末期内径与CABG 术后血管再狭窄程度有关，而与其他变量无关。OR 的点估计和置信区间结果显示桥龄越大、心脏病类型为急性冠状动脉综合征以及左室舒张末期内径越大，则血管无狭窄的可能性越低；原位靶血管病变支数2 支相对于3 支而言，血管出现无狭窄的可能性越高。

3 讨 论

本文主要采用了LOGISTIC 过程对多值有序资料拟合累积logistic回归模型，在变量筛选方面分别选用了常用的逐步、向前和向后三种方法，结果表明三种方法最后纳入了相同的自变量，参数的极大似然估计也相同，但三种方法在变量筛选过程方面实则不同，具体的变量筛选原理可参阅文献［5］。从多种筛选自变量方法产生的回归方程中选择最优的回归方程，可参考的标准主要有以下几条：第一，整个回归方程以及筛选出的自变量具有统计学意义，并在专业上有合理的解释；第二，若回归方程中所含自变量的个数相同，取赤池信息标准值（Akaike information criteria，AIC）较小者，其次模型的结果以简单为主。本案例中三种变量筛选方法的AIC 值均为409.338，且纳入的自变量相同，故最后结果相同。

除此之外，累积logit 回归分析多值有序数据时依然还需要注意一些问题：（1）平行线假设：在拟合有序logistic 回归时，需要对拟合的J-1 个方程对应的累积概率曲线的平行性进行检验。当平行线假设未满足时，说明资料不适合有序logistic 回归模型，应采用多值名义的logistic 回归模型；（2）个体独立性：拟合多值有序logistic 回归模型时，要求研究个体之间是相互独立的，即不存在组内个体同质、组间个体异质的现象，若资料不满足该情况则可以采用多值有序多水平的logistic 回归分析；（3）在建模时，还可以引入一些派生自变量（如连续变量的平方项、交叉乘积项等）参与自变量的筛选，有时可能获得拟合优度更高的回归模型。因篇幅所限，此处暂不赘述，可参阅文献［6-9］。