回转体潜器在循环水槽中垂直面大攻角操纵性试验
梁笑阳, 马 宁, 刘 晗, 顾解忡
(上海交通大学 a. 船舶海洋与建筑工程学院; b. 海洋工程国家重点实验室;c. 高新船舶与深海开发协同创新中心,上海 200240)
潜器作为开发海洋空间与资源的重要工具日益受到行业内的关注.在潜器作业过程中,常会以不同的航速、航向或姿态航行,良好的操纵性是潜器安全航行、高效作业的重要保证.为获得准确可靠的操纵性预报,有必要对潜器的水动力性能进行研究.
研究潜器操纵性的方法主要分为数值计算和试验研究两类,其中试验研究作为获得其水动力性能准确数据的最可靠途径而备受国内外研究者的重视[1].Nomoto等[2]利用平面运动机构(PMM)对“海豚3K”型带缆潜器(ROV)的1∶4简化模型进行操纵性试验,测试并分析其全攻角、全漂角、横摇、纵摇、艏摇等水动力特性,建立潜器本体完整的空间运动方程,并对不同海况与压载状况下的带缆潜器的姿态与受力进行仿真.张华等[3]在中国船舶科学研究中心的风洞实验室及旋臂水池实验室对扁平型潜器模型进行大机动状态下的水动力试验,并基于试验数据提出分段回归方法归纳水动力表达式,建立了一个相对完整的、可描述扁平型潜水器各种空间大机动运动的统一数学模型.Avila 等[4]基于Morison公式研究LAURS型ROV的水动力性能,开展了包括±100° 测量区间大漂角、纯横荡等工况的PMM试验,并通过对比试验与由系统辨识(SI)法估算的结果,验证了两者的阻力及升力系数的分析结果是高度一致的.Saeidinezhad 等[5]应用烟流显性技术在风洞中对某艏部非对称潜器进行攻角为-10°~27° 工况下的流场分析与水动力测定.研究表明随着攻角值的增大,升力与阻力系数均增大,且观测到的流动分离主要发生在艏部尖端处.曹建等[6]在循环水槽中开展了某带吊舱水下无人航行器的水动力试验,研究内容包括阻力试验、纯升沉及纯横荡试验、纯俯仰及纯艏摇试验,获得了相应的水动力系数,并对该航行器的操纵性能进行了全面的分析与评价.
潜器的操纵性试验常选在风洞、悬臂水池、拖曳水池等设备中进行,鲜少在循环水槽(CWC)中进行试验.相较于前者,循环水槽因不受拖车及轨道限制、模型安装方便、姿态与形位的调节范围更广、水以一定速度循环流动、可长时间测试等优势,更适用于研究大长径潜器在大攻角状态下的操纵性.针对这一现状利用PMM装置,在上海交大风洞循环水槽中对半尺寸全附体SUBOFF潜器模型开展垂直面操纵性试验研究.研究内容主要包括:在不同流速下测定潜器在±60° 攻角间的水动力参数,建立潜器垂直面大攻角工况下的运动模型,以及分析该试验的不确定度.
1 试验设计
1.1 试验系统
如图1所示,潜器垂直面操纵性试验系统主要包括被测对象、测试设备、控制系统、测量系统等单元.其中,被测对象为半尺寸SUBOFF潜器模型,外形选用美国国防高级研究计划局(DARPA)于1989年公布的全附体5470型模型的外形[7],附体包括围壳与“十”字型尾舵.潜器模型总长L=2.178 m,最大直径D=0.254 m,排水量V=87.72 kg.测试设备主要有立式多功能水槽与PMM.循环水槽为垂直型结构,敞开式测试段位于水槽上部,测试段水道两侧及底部均安装玻璃以便试验观测与拍摄.循环水槽的主尺度、流速等各项参数如表1所示.PMM由伺服电机驱动,加装限位器后的运动幅度为纵向位移1 m(精度0.01 mm),绕垂向轴70° 转动(精度0.01°).控制系统与测量系统包括各控制箱、位移/角度传感器、三分力仪、温度计、信号转换器、测量软件、台式计算机等仪器设备.

图1 潜器垂直面操纵性试验系统示意图Fig.1 Layout for the test on maneuverability in the vertical plane of the submersible

表1 立式多功能循环水槽的主要参数Tab.1 Parameters of the CWC
1.2 潜器模型布置
试验潜器模型的布置如图2所示.剑柱(即支柱)下端与潜器模型在左舷连接,连接点的纵向坐标与潜器重心的纵向坐标相重合;剑柱上端与三分力仪测力面通过法兰相接,三分力仪的另一端面连接在PMM的运动支柱上.模型侧放于水槽中,中纵剖面平行于水平面,中轴线位于工作段池壁的对称面上,距池底0.873 m处.此时的模型布放可满足忽略水池边界影响的条件,即模型表面距离自由面、池壁、池底等边界的最小距离超过其最大直径的2倍,且阻塞比小于25%[8-10].同时,利用PMM机构研究潜器模型的垂直面操纵性水动力性能,为了方便安装潜器模型,在试验中增大攻角测量范围.

图2 潜器模型布放示意图与实物图Fig.2 The schematic diagram and actual layout of the submersible model
1.3 试验工况
潜器模型的垂直面操纵性试验于2018年5月中旬完成,试验内容包含不确定度测试与正式试验两部分内容,具体工况如表2所示.其中:t为水温;uCWC为循环水槽流速;α为潜器攻角.
表2 潜器模型的垂直面操纵性试验的主要工况
Tab.2 The main conditions of the test on maneuverability in the vertical plane of the submersible model

试验内容t/℃uCWC/(m·s-1)α/(°)不确定度试验24.21.230正式试验24.21.0,1.1,1.2-60,-55,-50,-45,-40,-35,-30,-25,-20,-15,-10,-5,0,5,10,15,20,25,30,35,40,45,50,55,60
2 试验的不确定度分析
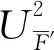
(1)
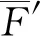

(2)
(3)
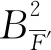
将表3中的各子项参数值代入式(1)~(3)中,试验测量无因次水动力项X′,Z′和M′总不确定度的计算结果如表4所示.由表4可知,各无因次水动力项不确定度的数值相较试验测得的水动力无因次值而言非常小,表明试验测量系统稳定可靠,测量结果精度较高.
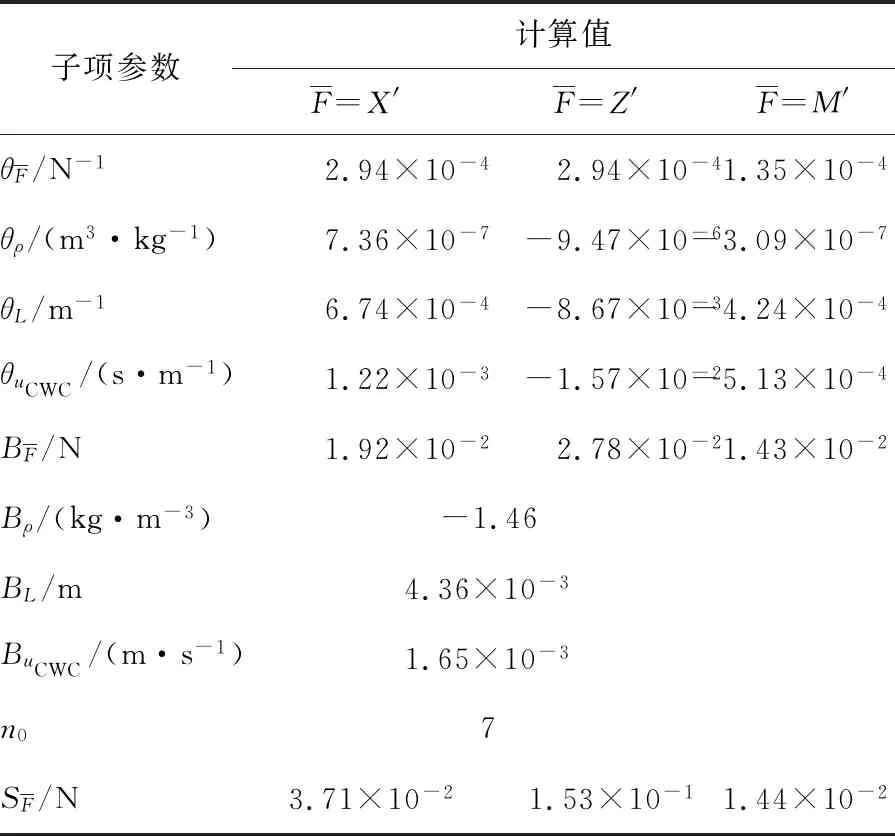
表3 B和P中各子项计算值Fig.3 The calculated values of the subitems in B and P
表4 试验测量无因次水动力项的总不确定度
Tab.4 The total uncertainty of the measured dimensionless hydrodynamic forces and moment

iUi×102Ui|i|%X'2.801.12Z'11.60.36M'1.090.48
3 结果与讨论
3.1 操纵性试验结果
采用ITTC和造船与轮机工程学会(SNAME)术语推荐的坐标系[1],如图3所示.运动坐标系为G-xyz,x轴沿艇模中线指向艏部,y轴垂直于艇模的中纵剖面指向右弦,z轴指向艇底;固定坐标系E-ξηζ原点可任意选取水面或地面上的某一点,ξ轴与循环水槽流速方向一致,η轴与ξ轴在同一水平面内,其正向按顺时针方向与ξ轴之间的夹角为90°,ζ轴指向地心.
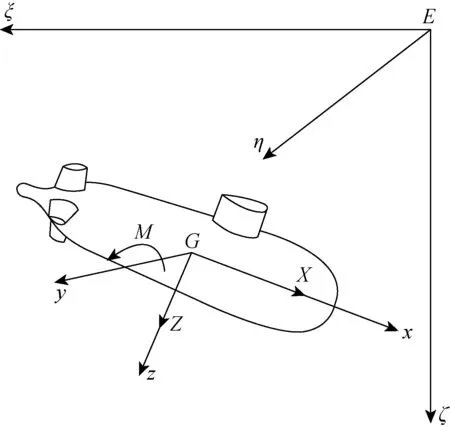
图3 固定坐标系和运动坐标系Fig.3 Fixed coordinate system and moving coordinate system
对试验测得的X,Z和M进行无因次化处理,若令ρ=997.25 kg/m3,水动力无因次化公式为
(4)
计算得到的水动力无因次参数值X′,Z′与M′如图4所示.
由图4(a)可知:在攻角为±60° 的测量区间内,流速不同而攻角相同的X′值高度一致,曲线高度重合;当α∈[-60°,0°]时,X′值随α的增加而减小; 当α∈[0°,60°]时,X′值随α的增加先减小后增大;X′的最大值出现在α=-60° 时,最小值出现在α=20° 时,显示出弱非线性与较为明显的非对称性.由图4(b)可知:不同流速下相同攻角的Z′曲线也显示了高度的重合性,但当α∈[50°,60°]时,Z′值随水槽流速的变化而略有分化,水槽流速越大,Z′值越小;当α=0° 时,Z′值接近于0;Z′值随着α的增大而大,最大值出现在α=±60° 时,曲线整体显示出弱非线性与弱对称性.由图4(c)可知:当α∈[-25°,25°]时,流速不同而攻角相同的M′曲线显示了较为良好的重合性;随着α的增加,不同水槽流速下的M′曲线出现了分离现象,且这种分离现象无明显规律,其中当uCWC=1.0 m/s时的曲线偏差最大;在α=0° 时,M′值接近于0; 当α∈[-25°,25°]时,M′值随着α的增大而增大; 当α∈[25°,60°]时,曲线开始时变化平缓,随后先增大后减小,正攻角下最大值出现在α=45° 时; 当α∈[-60°,-25°]时,M′曲线先减小后增大随后再次减小,负攻角下最大值出现在α=50° 时,曲线整体显示出较明显的非线性与非对称性.
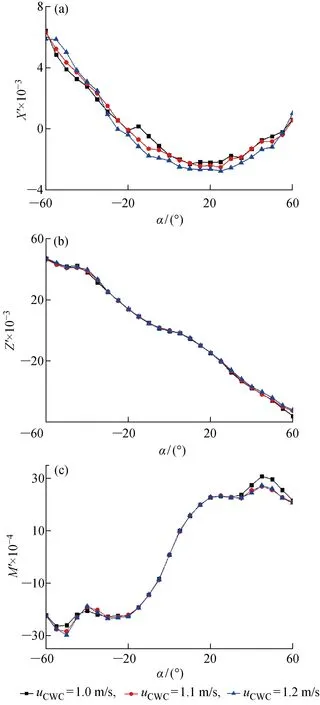
图4 无因次水动力值随α的变化曲线Fig.4 The dimensionless hydrodynamic forces and moment changes with α
无因次水动力值在大攻角范围内均显示出非对称性与非线性,这种特性随着攻角值的增大而愈发明显.产生这种现象主要有两个原因:① 随着攻角值的变大,潜器模型的迎流截面积有所增加,周围流场的雷诺数也开始增大,潜器表面的流动分离现象逐渐增强,潜器中后段背流表面渐渐形成了驻留涡、脱落涡等涡系结构,流场结构变得更为复杂;摩擦阻力与黏压阻力随之变化,且变化幅度不一致,造成了各向水动力的非线性变化.② 附体是影响水动力非对称性的主要因素.在小攻角范围内,附体迎流截面积较小,对裸艇体周围流场结构的干扰有限,此时水动力系数的非对称性与非线性较弱;当潜器处于大攻角姿态时,这种干扰不可忽略,且此时附体附近的流域速度、压力变化剧烈,局部湍流度与整个流场的湍流度有较大的差异,使得水动力的非线性和非对称性更为明显.
图5所示为本试验(SJTU)与DARPA试验[14]的无因次水动力值对比曲线.需说明的是,此时α∈[-15°,15°],测得的无因次水动力值可以用如下线性操纵性方程[1]表达:
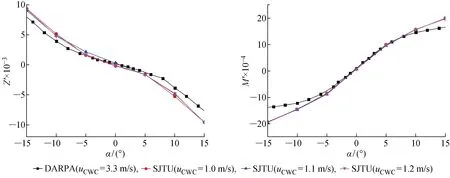
图5 SJTU与DARPA试验结果对比Fig.5 The comparison of the results between SJTU and DARPA
(5)
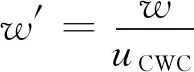
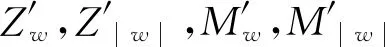

表5 SJTU与DARPA工况及结果对比Tab.5 The comparison of the test conditions and results between SJTU and DARPA

图6 3组试验的CFD仿真速度云图与Q判定下的流动分离示意图Fig.6 The calculated cloud charts of the velocity and the flow separation diagrams with Q-Criterion by CFD of three test groups

图7 二阶标准方程与分段函数拟合Fig.7 The comparison of fitting methods between the second order standard equations and the piecewise function
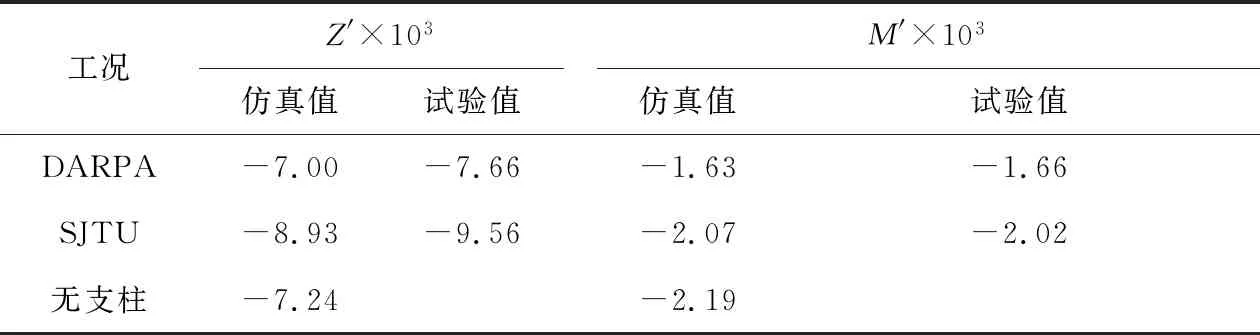
表6 CFD结果与试验结果对比Tab.6 The comparison of the CFD results and test results
3.2 操纵性运动数学模型的建立
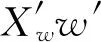
(6)
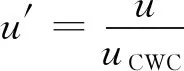
M′=
(7)
以uCWC=1.2 m/s工况下M′的试验数据为研究对象,分别用二阶标准方程与分段函数两种方法进行曲线拟合,计算结果如图7所示.由图7可知,使用分段函数进行拟合时,数据点与拟合曲线更为接近,更能准确地描述M′随α的变化情况.以整体测量数据为样本点,计算二阶标准方程曲线拟合优度判定系数R2=0.98,分段函数方程曲线拟合优度判定系数R2=1.00,显然分段函数模型与试验数据的拟合程度更高[17].潜器垂直面操纵性的水动力表达式确立之后,采用最小二乘法对表达式各子项水动力系数的无因次值进行计算,计算结果如表7所示.
表7 试验水动力系数的无因次值
Tab.7 The dimensionless values of the hydrodynamic forces and moment

水动力系数计算值 水动力系数计算值 X'w-3.57×10-3Z'w7.23×10-3X'uu-2.01×10-3Z'ww-2.56×10-2X'ww3.66×10-4Z'ww-1.07×10-2X'ww4.75×10-3M'(+)01.96×10-2Z'0-7.57×10-4M'(+)w-8.97×10-2Z'w-3.68×10-2M'(+)ww1.51×10-1M'(+)www-8.14×10-2M'ww-1.34×10-2M'08.03×10-5M'(-)0-5.53×10-2M'w1.11×10-2M'(-)w-2.43×10-1M'w-2.22×10-4M'(-)ww3.63×10-1M'ww1.37×10-4M'(-)www-1.77×10-1
4 结论
通过循环水槽模型试验,研究半尺寸SUBOFF潜器模型在大攻角工况下的垂直面操纵性,合理地归纳水动力表达式并拟合了各向水动力系数,进而建立可靠的垂直面空间运动的数学模型.研究结果表明:
(1) 试验测得的无因次水动力值在大攻角范围内显示出非对称性与非线性,这种特性随着攻角值的增大而愈发明显.产生这种现象的原因是潜器模型附近的流场结构随攻角值发生了变化,以及附体造成的模型几何的非对称性.在常攻角范围内比较SJTU与DARPA结果,两者的曲线走势显示了较为良好的一致性,数值上的差异主要受支柱、雷诺数、测试流域几何尺寸等因素的影响.
(2) 在标准方程的基础上归纳潜器垂直面操纵性方程,对X′保留非对称项,同时利用分段函数归纳M′的表达式,修正后的方程可以准确地描述水动力强烈的非对称性与非线性变化.
(3) 通过分析试验的不确定度,表明测量系统稳定可靠,测量结果精度较高,并验证了潜器模型垂直面操纵性试验的正确性.

