单箱双室波形钢腹板组合箱梁横向内力研究
王兆南,张元海
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
波形钢腹板组合箱梁自重小、受力性能良好,在桥梁中有广泛的应用前景。这种组合结构形式在偏心荷载作用下往往产生较大的横向内力,因此受到了科研设计人员的广泛关注,国内外已有不少文献对波形钢腹板组合箱梁的横向内力进行了研究。文献[1]研究了单箱单室矩形截面波形钢腹板组合箱梁桥的横向受力。文献[2-3]采用框架分析法对单箱单室波形钢腹板箱梁桥面板横向内力进行了研究,认为腹板与顶板的线刚度比是影响桥面板横向内力的重要因素。文献[4]采用弹性薄板理论对单箱单室波形钢腹板组合箱梁横向内力及横向有效分布宽度进行了理论分析和试验研究。文献[5-6]对带悬臂的单箱单室箱梁桥横向内力进行了分析。文献[7]对单箱单室斜腹板箱梁横向内力进行了分析,并进行了横向内力的参数影响分析。文献[8]研究了波形钢腹板梁的弯扭特性。文献[9]采用LUSAS有限元软件对影响波形钢腹板受力特性的板厚、波长等参数进行了研究。文献[10-11]采用弹性支承代替框架分析法中的刚性支承,对单室连续弯箱梁桥的横向内力进行了计算分析。文献[12]采用有限条法分析双室箱梁的顶板横向内力。文献[13]基于虚拟框架法,采用有限元对单箱三室梯形箱梁的横向内力进行了研究,认为虚拟框架法计算简便且实用。文献[14]研究了材料非线性状态下钢筋混凝土箱梁横向受力的有效分布宽度。
上述文献主要针对单室箱梁的横向内力进行研究,对多室箱梁横向内力的研究主要采用基于板壳、实体单元的有限元分析法或采用有限条分析法,而单箱双室波形钢腹板组合箱梁横向内力解析理论方面的研究很少。本文以框架分析法为基础,考虑箱梁截面畸变效应的影响,推导单箱双室波形钢腹板组合箱梁的横向内力计算公式,并分析波形钢腹板截面参数和组合箱梁宽高比对横向内力的影响。
1 虚设刚性支承的框架分析
在箱梁跨中沿梁轴方向截取单位长度的梁段,形成一个闭合框架,以传统框架分析法为基础,进行箱梁横向内力分析。先在框架上施加虚设的刚性支承,计算支承反力并进行框架横向内力计算,然后释放刚性支承,将支承反力反向加在框架上计算由于截面畸变产生的横向内力,最后将二者的结果叠加,得到偏心荷载作用下的最终横向内力。
采用横向框架模型计算横向内力时,有以下3条假定:
(1)组成框架各板件的轴向变形忽略不计,即认为箱形截面的周边不可压缩,横向应变为0;
(2)箱形梁发生畸变翘曲时,组成箱形截面的各板件作为各纵向板梁的横截面,分别满足平截面假定;
(3)忽略箱梁各板件厚度对翘曲的影响,即剪应力和翘曲正应力沿壁厚均匀分布。
图1为普通波形钢腹板一个波长范围内的形状,t为波形钢腹板的厚度,a为平直段长度,δ为波高,c为倾斜段的水平投影长度,α为波折角,w为波长,波形钢腹板绕z轴单位长度的横向抗弯惯性矩Iz=(3atδ2+tδ3/sinα)/(6w)。将波形钢腹板换算为相同横向刚度的混凝土截面,其等效厚度tc=Ebgt/E,Ebg为换算后钢腹板的表观弹性模量,E为混凝土弹性模量。目前设计中常用的波形钢腹板有w=1 600 mm的1600型、w=1 200 mm的1200型、w=1 000 mm的1000型三种类型。
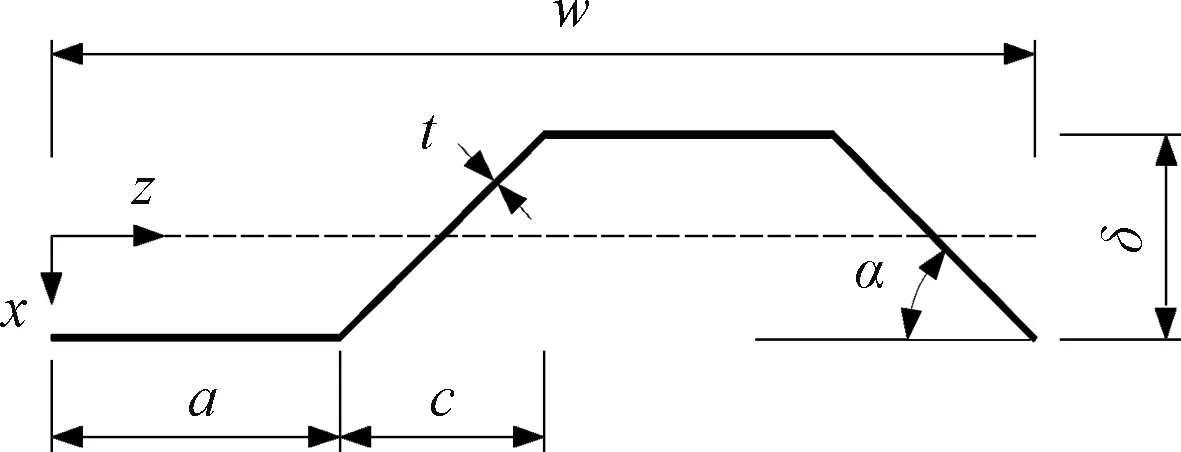
图1 波形钢腹板简图
图2为具有波形钢腹板的等截面矩形单箱双室组合箱梁,h为梁高,b为顶板宽度,b0为悬臂板加顶板的总宽度,t0、tc、tu分别为顶板、腹板和底板的厚度,悬臂板与顶板厚度相同,各角点分别用A、K、B、C、F、D表示。
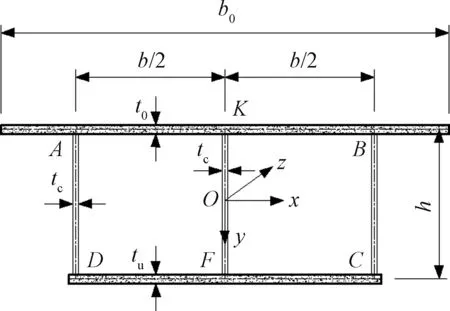
图2 单箱双室箱梁横截面简图
用框架分析法进行箱梁横向内力分析时,可取图3所示的力学分析模型。图3(a)所示的模型除了在底板施加竖向约束外,还在B点施加横向水平约束,即认为箱梁在偏心荷载作用下无侧移,图3(b)为许多文献中采用的只施加竖向约束的模型。本文将对两种模型的横向内力进行对比。图3中的点1~10为竖向荷载的加载位置。
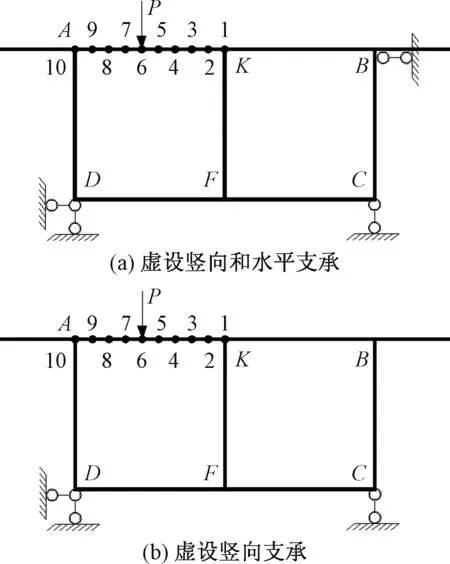
图3 单箱双室箱梁的横向框架力学分析模型
与单箱单室箱梁不同,单箱双室箱梁由于增加了一道腹板,使解算刚性支承的框架横向内力和分析双室箱梁的畸变都更复杂。与单室箱梁的畸变不同,双室箱梁的畸变可分为正对称畸变和反对称畸变,其中反对称畸变起主导作用[15],所以本文对畸变产生的横向内力只考虑反对称畸变的影响,使问题得到简化。
2 释放虚设支承的框架分析
释放虚设在框架上的支承,用反向支承反力取代,进行考虑畸变影响的框架内力分析,见图4,qh为反向支承反力分解的反对称竖向力,qdb为横向水平力。当采用图3(b)所示的分析模型时,结构上无横向水平力qdb,竖向力qh的大小将与图3(a)模型得出的值不同。本文通过箱梁畸变时框架上剪力差与内剪力之间的关系来分析箱梁畸变产生的横向内力。
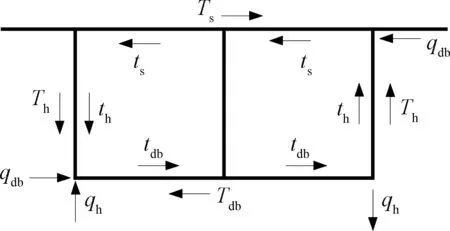
图4 反对称荷载与剪力差荷载
2.1 各板件力矩与框架上剪力差的关系
沿箱梁z轴向截取的单位长度框架上,作用有扭转剪力差ts、tdb、th和畸变剪力差Ts、Tdb、Th,见图4。
中间腹板上的剪力差是一对自相平衡的力,在列平衡方程时会相互抵消。根据角点处剪力流相等的关系,可以得到
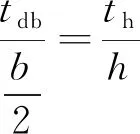
( 1 )
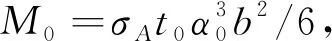
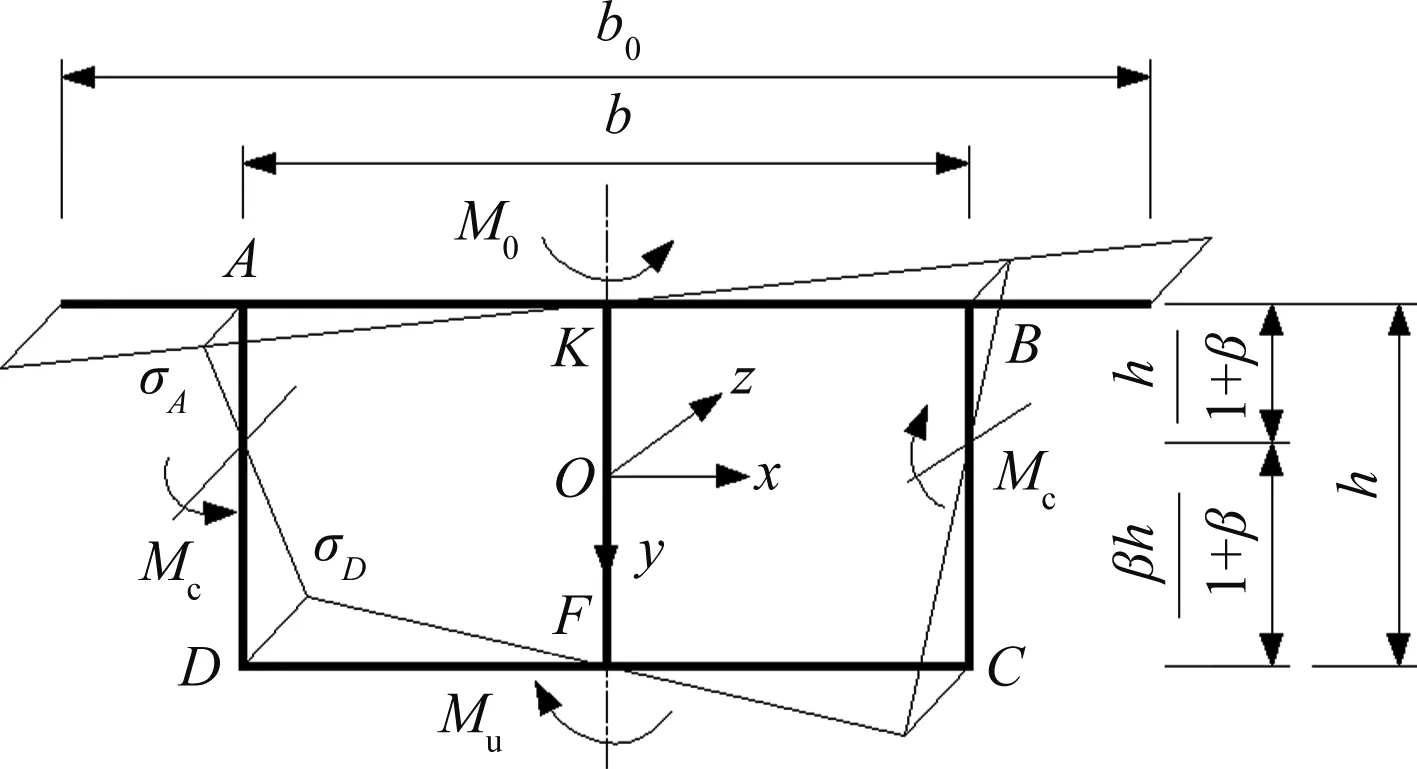
图5 畸变引起的各板件力矩
由绕y轴的力矩平衡条件Mhy+M0+Mu=0,可以求出系数β。根据各板件翘曲力矩与剪力的关系,可建立框架底板、腹板与顶板上剪力差之间的关系
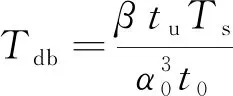
( 2 )
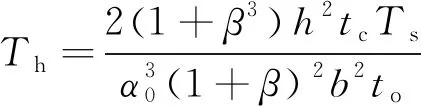
( 3 )
2.2 内剪力与框架上剪力差的关系
在反对称荷载作用下,沿框架各板件反弯点处截开,各板的内剪力见图6,Qs为顶板的内剪力,Qdb为底板的内剪力,腹板AD的内剪力为Qh1,腹板KF的内剪力为Qh2。由于箱梁在反对称荷载作用下内力呈反对称,因此腹板BC的内剪力与腹板AD的内剪力Qh1相等。
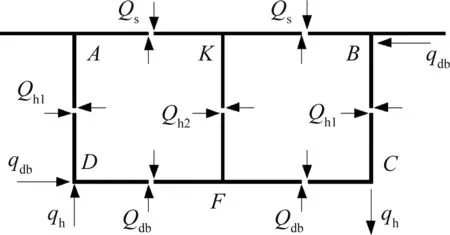
图6 框架内剪力示意
通过分析,可建立腹板与顶板、底板内剪力之间的关系
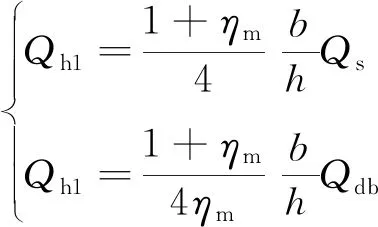
( 4 )
式中:ηm=[3+bIc/(hI0)]/[3+bIc/(hIu)],I0、Ic、Iu分别为框架各板件的面外惯性矩。通过内剪力Qh1表达的框架横向水平侧移为Δ=ξQh1/(128E),其中:ξ=b2(η1+η2+η3)/[nIcI0(η4+η5)],η1=(nbIc)3(81hI0+27nbIc),η2=51.75(nhbIcI0)2,η3=(hI0)3(15nbIc+hI0),η4=40.5(nbIc)2(nbIc+hI0),η5=1.5(hI0)2(9nbIc+hI0),n为波形钢腹板表观弹性模量与混凝土弹性模量的比值。
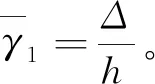
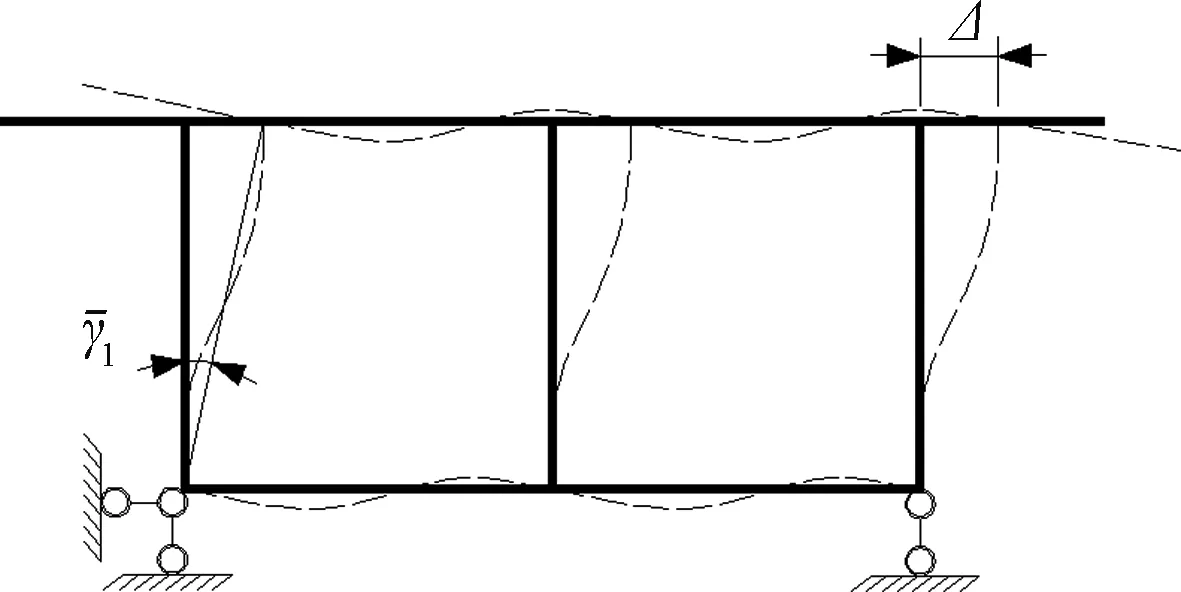
图7 框架横向水平侧移
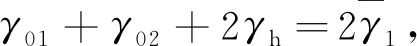
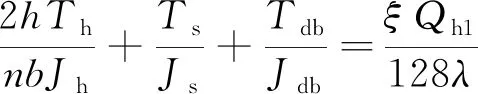
( 5 )
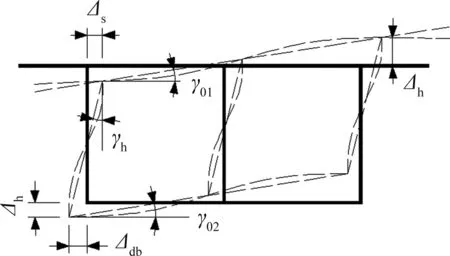
图8 箱梁畸变变形
2.3 有虚设横向水平约束的框架内力平衡关系
对应于图3(a)的分析模型,框架在B点有横向水平约束,框架剪力差与反对称荷载使框架受力平衡。根据图4和图6,由框架整体在x方向受力平衡条件可得
Ts-Tdb-2ts+2tdb+qdb-qdb=0
( 6 )
由框架左半部分y方向平衡条件可得
Qs+Qdb-Th-th+qh=0
( 7 )
由框架上半部分x方向平衡条件可得
2Qh1+Qh2+2ts-Ts+qdb=0
( 8 )
由框架下半部分x方向平衡条件可得
2Qh1+Qh2+2tdb-Tdb+qdb=0
( 9 )
取框架左半部分,对框架角点D建立力矩平衡方程,可得
b(Qdb+Qs)+4h(ts-Ts)=0
(10)
联立式( 1 )~式(10)解出内剪力Qs、Qdb、Qh1后,即可得到有虚设横向水平约束时由箱梁畸变产生的横向弯矩。
2.4 无虚设横向水平约束的框架内力平衡关系
对应于图3(b)的分析模型,框架在B点无横向水平约束,对框架进行剪力差和反对称荷载作用下的受力平衡分析,得到式(11)~式(13)。其中,式(11)由考虑框架整体x方向受力平衡得出,式(12)由考虑框架上半部分x方向平衡得出,式(13)由考虑框架下半部分x方向平衡得出。
Ts-Tdb-2ts+2tdb=0
(11)
2Qh1+Qh2+2ts-Ts=0
(12)
2Qh1+Qh2+2tdb-Tdb=0
(13)
联立式( 1 )~式( 5 )、式( 7 )、式(10)~式(13),即可求得内剪力Qs、Qx、Qh1,从而得到无虚设横向水平约束时由于箱梁畸变产生的横向弯矩。
将本节畸变产生的框架横向内力与第1节刚性支承框架的横向内力叠加,即得偏心荷载作用下,考虑箱梁畸变影响时的单箱双室波形钢腹板组合箱梁最终横向内力。
3 数值算例
本文取跨度40 m的等截面简支单箱双室波形钢腹板组合箱梁,对理论分析进行有限元验证。箱梁截面高度2 m,顶板加悬臂板总宽度6m、厚度0.3 m,底板宽4 m、厚度0.3 m。采用1600型波形钢腹板,厚度0.024 m,混凝土弹性模量E=30 GPa,钢材弹性模量Es=210 GPa。顶板上沿梁轴z方向施加荷载P=100 kN/m,计算箱梁框架角点的弯矩,采用板单元建模分析,按图3所示的两种分析模型分析虚设的横向水平约束对横向内力的影响。
3.1 虚设横向水平约束对横向内力的影响
取加载位置6点处的理论计算数据分析虚设横向水平约束对横向内力的影响。
3.1.1 对刚性支承框架横向内力的影响
在竖向偏心荷载P作用下,框架B点是否虚设横向水平约束时,计算的刚性支承框架横向内力比较如表1所示。由表1可以看出,刚性支承框架各角点弯矩偏差率最小为0.9%,最大为2.6%。从对刚性支承框架横向弯矩的影响来分析,两个分析模型计算结果差别很小。
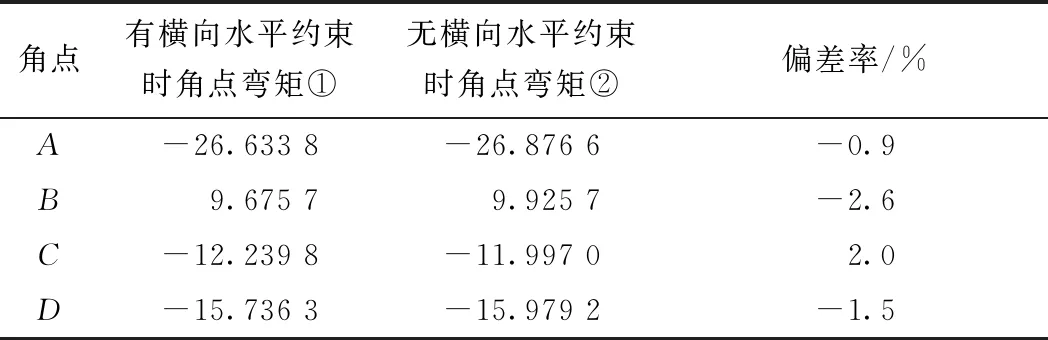
表1 刚性支承框架角点横向内力比较
注:弯矩单位为kN·m/m;偏差率=(①-②)/①×100%。
3.1.2 对框架最终横向内力的影响
在反向支承反力荷载和剪力差作用下,按框架B点有无虚设横向水平约束计算的框架内剪力结果比较如表2所示。

表2 释放刚性支承后框架的內剪力
求出框架的内剪力后,根据框架节点力矩平衡可进一步求得由畸变产生的框架横向内力。将由畸变产生的横向内力与刚性支承框架的横向内力叠加,得到考虑了箱梁畸变的框架最终横向内力,结果如表3所示。
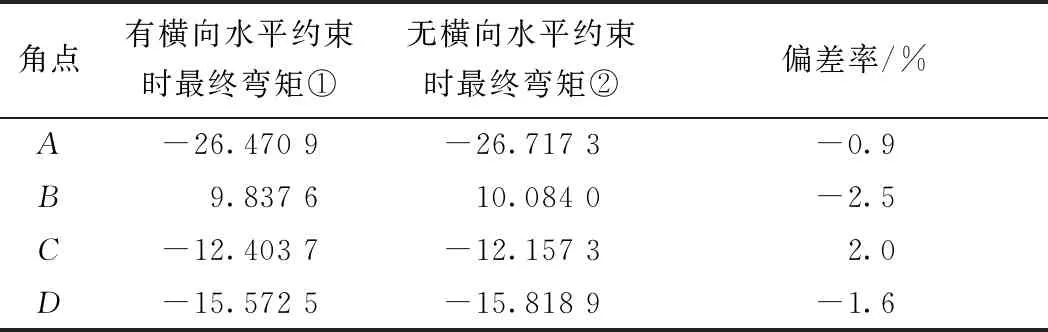
表3 横向水平约束对箱梁横向内力的影响
注:弯矩单位为kN·m/m;偏差率=(①-②)/①×100%。
从表3可以看出,两种分析模型对箱梁横向内力的影响偏差不超过2.5%,即是否虚设横向水平约束对箱梁最终横向内力的影响不明显。为使箱梁横向内力分析简易且不失准确性,箱梁横向内力的计算可以采用无横向水平约束的分析模型。
3.2 框架横向内力理论计算值与有限元值对比
现给出按图3(b)所示分析模型得到的横向内力理论值与有限元值的对比分析,见图9、图10。有限元分析时采用板单元,加载位置从1点移动到10点,见图3(b)。

图9 加载位置变化时框架A、B点横向弯矩
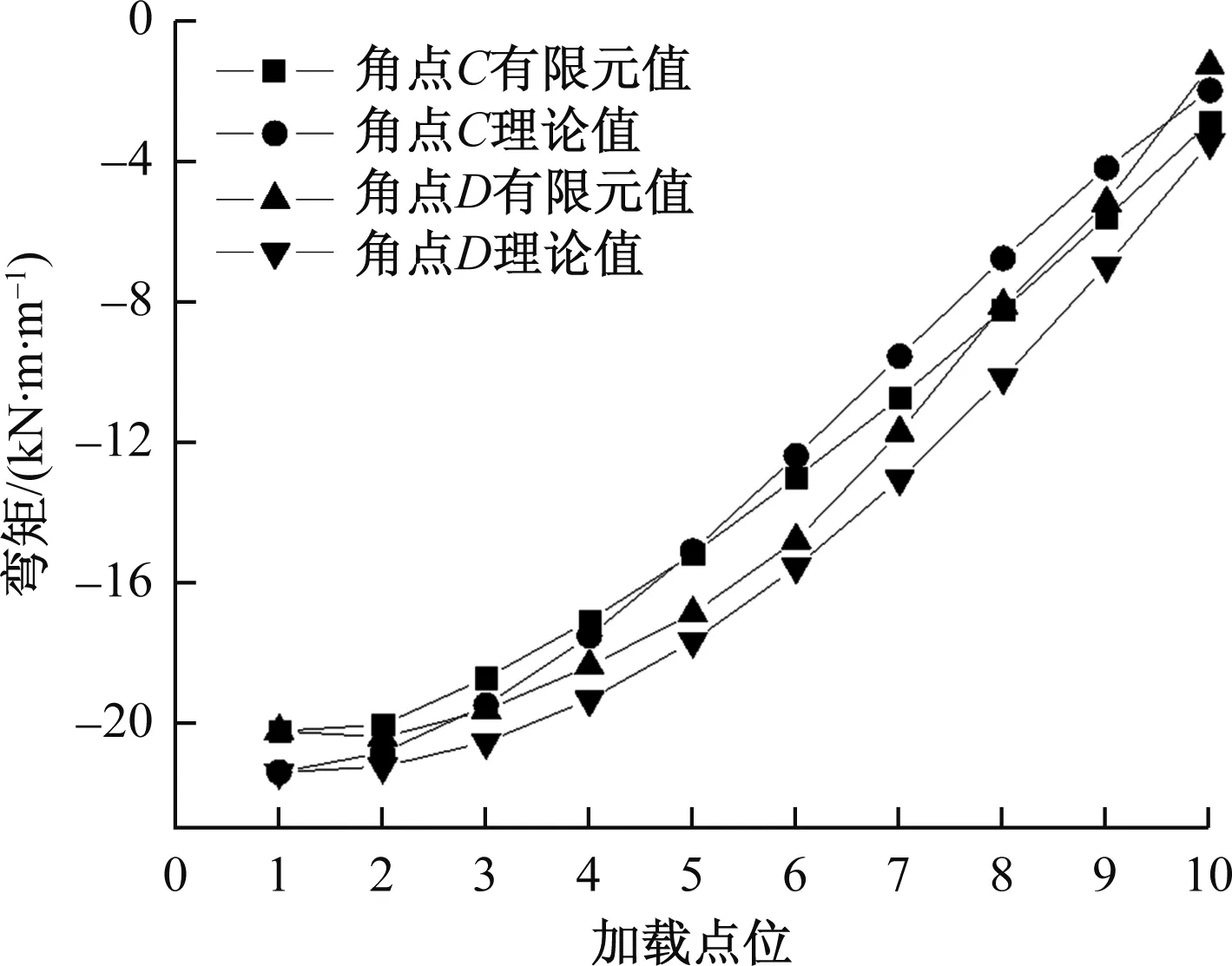
图10 加载位置变化时框架C、D点横向弯矩
从图9和图10可以看出,当加载位置从箱梁顶板1点处逐渐移到10点处时,角点A的弯矩绝对值先逐渐增大,随后减小;B、C、D点的弯矩绝对值随着加载位置的移动逐渐变小。箱梁顶板上作用竖向移动荷载时,角点A、B、C、D弯矩的大小呈现不同的变化。由于篇幅所限取加载位置5点和6点的计算数据,列入表4、表5。
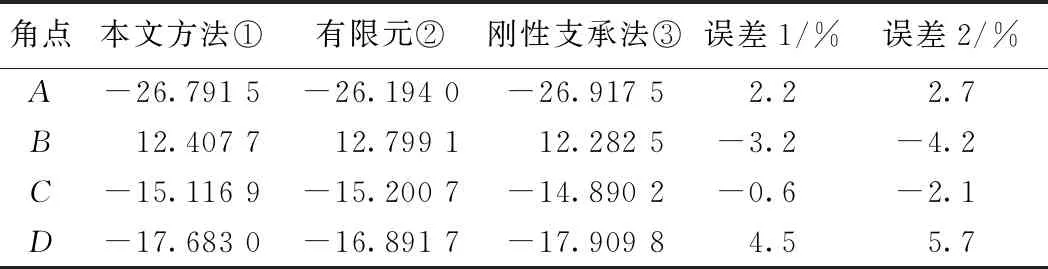
表4 荷载作用于5点时各角点横向弯矩比较
注:误差1=(①-②)/①×100%,误差2=(③-②)/③×100%,弯矩单位为kN·m/m。
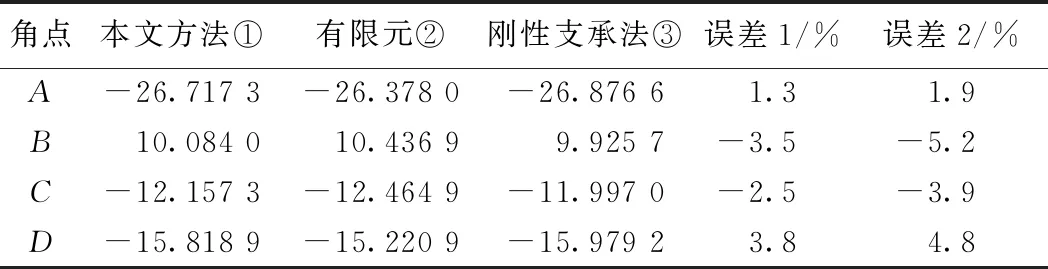
表5 荷载作用于6点时各角点横向弯矩比较
注:误差1=(①-②)/①×100%,误差2=(③-②)/③×100%,弯矩单位为kN·m/m。
加载位置在5点时,角点弯矩计算精度如表4所示。当加载位置在6点时,框架角点A的误差1为1.3%,误差2为1.9%;B点误差绝对值由5.2%降至3.5%;C点误差绝对值由3.9%降至2.5%;D点误差绝对值由4.8%降至3.8%,见表5。从分析结果来看,由于考虑了畸变,本文的理论计算值比刚性支承的框架计算结果更加符合实际情况。
4 参数分析
本文考虑波形钢腹板厚度t、波折角α、波长w及箱梁宽高比的变化对角点横向弯矩的影响。荷载P作用于顶板A、K连线的中点,大小不变,利用有限元板单元进行分析。本节的横向弯矩提高率为

(14)
4.1 板厚、波折角、波长的影响
保持箱梁高、宽不变,顶板、底板尺寸不变,改变腹板厚度和波形钢腹板类型进行分析。波形钢腹板厚度从9 mm以3 mm为增量增加到24 mm,波长选取国内常用的3种型号,即1000型、1200型、1600型,对应波折角分别为45°、36.53°、30.74°。
4.1.1 对A、B点横向弯矩的影响
取3种类型波形钢腹板,波形钢腹板厚度、波折角、波长变化对框架A、B点横向弯矩的影响,见图11。从图11可以看出,随着板厚的增加,A、B点弯矩值逐渐增大,当板厚从9 mm增加到24 mm时,A点横向弯矩变化显著,其提高率最大为216.4%,B点弯矩提高率最大值为16.0%。板厚相同的情况下,波长和波折角这两个参数对A、B点横向弯矩的影响不明显,其横向弯矩提高率绝对值最大不超过11.7%。
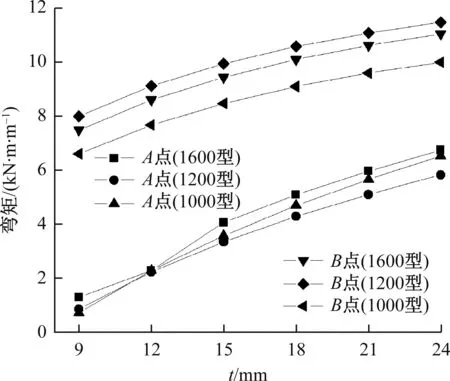
图11 腹板厚度变化时A、B点横向弯矩
4.1.2 对C、D点横向弯矩的影响
同理对C、D点的横向弯矩进行分析,见图12。由图12可以看出,随着板厚的增加,C、D点弯矩值逐渐增大,当板厚从9 mm增加到24 mm时,C点横向弯矩的提高率最大为23.1%,D点弯矩提高率最大值为8.6%。在板厚相同的情况下,C、D点各自横向弯矩由大到小依次为1000型、1200型、1600型,C点横向弯矩的提高率最大为18.2%,D点则为35.8%,可以看出波折角的变化对C、D角点横向弯矩的影响较大。
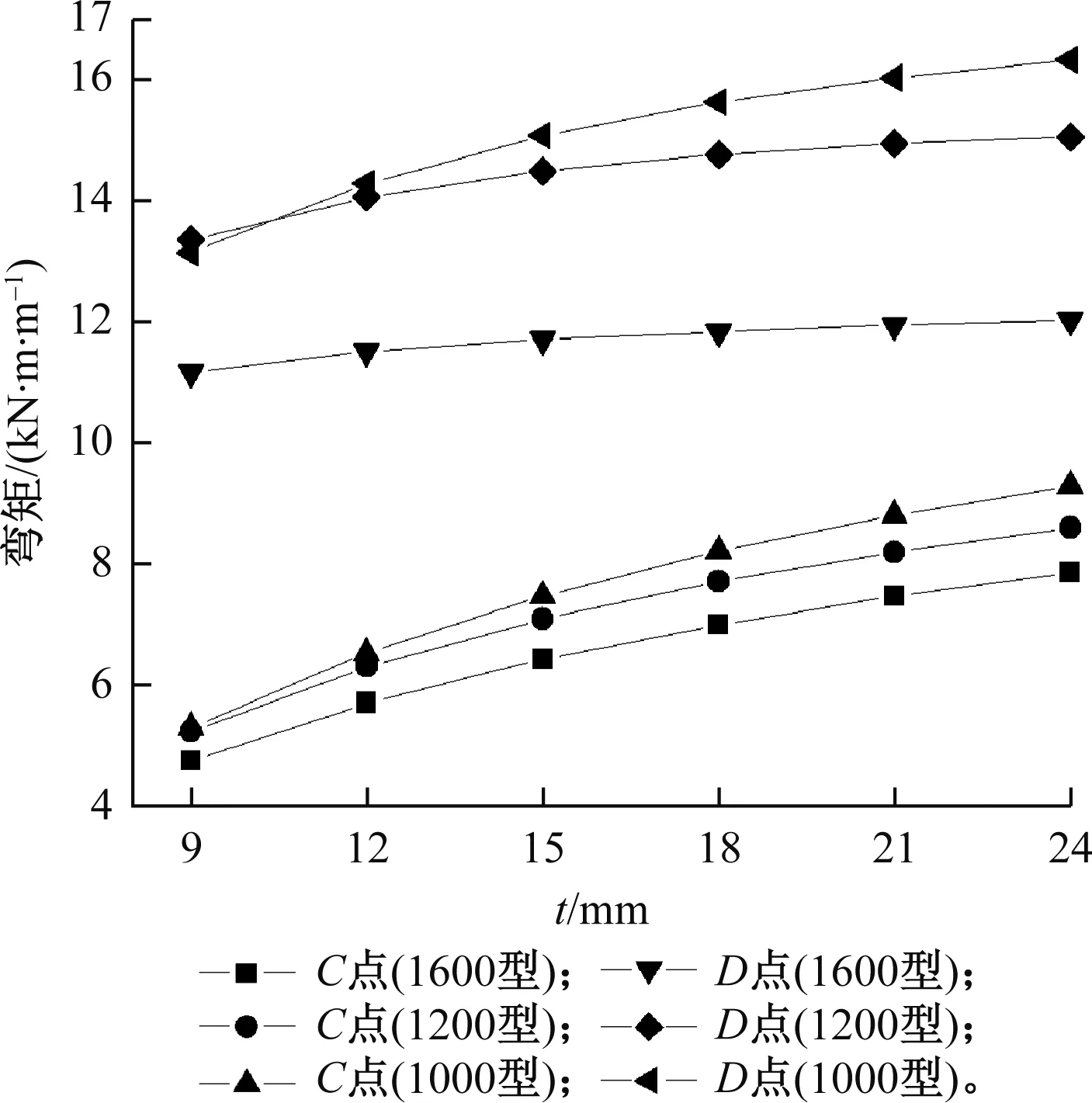
图12 腹板厚度变化时C、D点横向弯矩
由以上分析可知,随着波形钢腹板厚度的增加,箱梁框架A、B、C、D角点处横向弯矩逐渐增大。波形钢腹板波长、波折角变化,对顶板与边腹板角点处横向弯矩的影响较小;波折角的变化,对底板与边腹板角点处横向弯矩的影响较大。
4.2 宽高比的影响
箱梁宽从4 m开始以2 m为增量逐渐增加到12 m,梁高以0.5 m为增量从2 m逐渐增加到4 m,研究箱梁宽高比b/h从2逐渐增加到3的过程中,波形钢腹板组合箱梁角点横向弯矩的变化规律,见图13。波形钢腹板采用1600型,板厚0.024 m,图13中的箱梁宽高比分别为2、2.4、2.67、2.86和3。
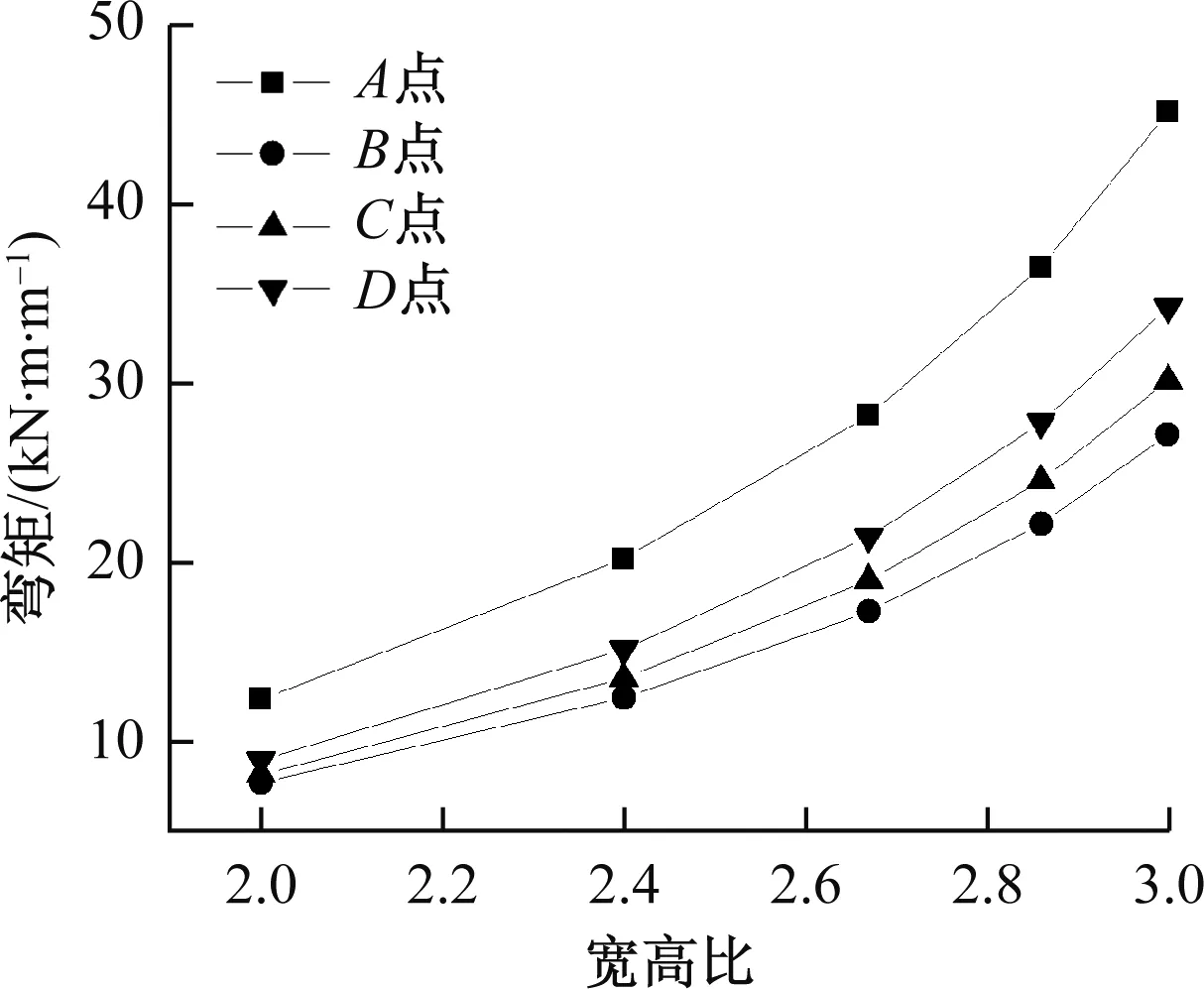
图13 宽高比变化时箱梁角点横向弯矩
由图13分析得到,随着箱梁宽高比的增加,单箱双室波形钢腹板组合箱梁框架角点横向弯矩逐渐增大,当宽高比超过2.4时,框架各角点横向弯矩变化显著。随着宽高比的增加,角点A横向弯矩的变化比其他角点明显,当宽高比从2变化到3时,其横向弯矩提高率单次最大为63.5%,宽高比较大时,横向弯矩的增大更为显著。
5 结论
本文通过对单箱双室波形钢腹板组合箱梁横向内力的研究,得到以下结论:
(1) 以框架分析法为基础,给出了考虑畸变影响时单箱双室波形钢腹板组合箱梁的横向内力计算公式。经有限元验证,理论值与有限元值吻合较好,考虑箱梁畸变影响的横向内力比刚性支承法计算的结果更加符合实际情况。
(2) 单箱双室波形钢腹板组合箱梁横向内力分析中是否虚设横向水平约束对箱梁横向内力计算的影响较小,对横向内力最终值的影响不超过2.5%。为使箱梁横向内力计算过程简易且不失准确性,可以采用不虚设横向水平约束的分析模型。
(3) 波形钢腹板截面参数变化将会影响单箱双室组合箱梁各角点的横向弯矩。板厚增大,各角点的横向弯矩增大;波折角的变化对底板与边腹板角点处横向弯矩的影响较大。
(4) 波形钢腹板单箱双室组合箱梁宽高比的变化将会影响箱梁各角点的横向弯矩。随着宽高比的增加,箱梁各角点的横向弯矩也增大,当宽高比较大时,横向弯矩的增大更为显著。

