高速动车组雷电波侵入特性及传播规律研究
曹保江,宋勇葆,魏文赋,高国强,吴广宁
(西南交通大学 电气工程学院,成都 610031)
接触网是高速铁路牵引供电系统的重要组成部分,其所铺设的地方多包含山区、丘陵等地区,长大隧道和高架桥占全线比重大,接触网遭受雷击的概率较高[1-3]。以京广高速铁路广东段接触网跳闸数据为例,从2009年至2013年4年间,共发生361件跳闸事件,发生绝缘子闪络或破损事件共140件。国内外对接触网雷击过电压的防护措施不尽相同,日本将高速铁路划分为A、B和C三个等级,对个别等级线路采取全线架设避雷线的防护措施。德国采用避雷器来限制接触网雷击过电压。国内学者提出将架空地线(PW线)抬高至馈线(F线)以上兼做避雷线以及在F线绝缘子安装带串联间隙避雷器的方法。通过对比分析升高保护线或回流线以及单独架设避雷线均能提高接触网耐雷水平,在落雷密度大且雷害事故严重的地区采取单独架设避雷线的方式效果更好[4]。我国京广、京津、京沪高速铁路在雷害多发地区正线锚段关节处、电分相关节处、长度2 000 m及以上隧道等重点位置设置带脱离器的氧化锌避雷器。研究表明,接触网遭受直击雷,并造成雷击跳闸占总跳闸事件的95%~98%,绝缘子闪络、接触网跳闸的主要原因为直击雷,因此高速铁路接触网的防雷应主要考虑防护直击雷,而不是感应雷[5]。当接触网遭受雷击时,雷击点临近支柱绝缘子先闪络放电,雷电流通过支撑绝缘子泄放到大地中,形成的雷电冲击过电压沿接触网传播到动车组高压系统[9]。
高速动车组通过在车顶高压系统中安装氧化锌避雷器来防护雷电过电压侵入动车组高压系统对电气设备造成的威胁。目前针对牵引供电系统接触网耐雷水平及防雷措施的研究较多[6-8],现有设计规程主要根据绝缘配合的确定性法,通过将车载避雷器的保护水平乘以一定的配合系数来选择动车组高压系统被保护设备上的绝缘水平[9-10],缺少将接触网和动车组作为整体综合考虑传播至动车组高压系统的实际雷电冲击电压特性。另一方面,在确定动车组设备的雷电冲击绝缘水平时,准确预测高压系统雷电过电压水平,对于合理选择高压设备绝缘配合关系至关重要[11]。
针对上述问题,本文根据牵引网和动车组主要结构参数建立仿真模型,计算雷击T线(承力索/接触线)和F线不同位置时传播至动车组受电弓位置的雷电波波形特征,以及车载变压器雷电过电压波形特征及幅值范围。
1 模型建立
1.1 牵引供电系统模型
牵引网是由馈线、接触线、承力索、钢轨、回流线、变电所等组成的牵引供电回路。牵引网的几何结构如图1所示,本文采用频变参数模型作为悬挂导线的模型。为防止在所研究的时间范围内,传到两侧线路末端的反射波沿线路返回后对雷击点处过电压的影响,在线路末端分别连接一条长的、与所研究线路具有相同特性的线路。由于接触网支柱高度一般低于30 m,仿真采用集中电感模型来模拟支柱模型,该模型将支柱作为集中参数电感和接地电阻相串联[12]。
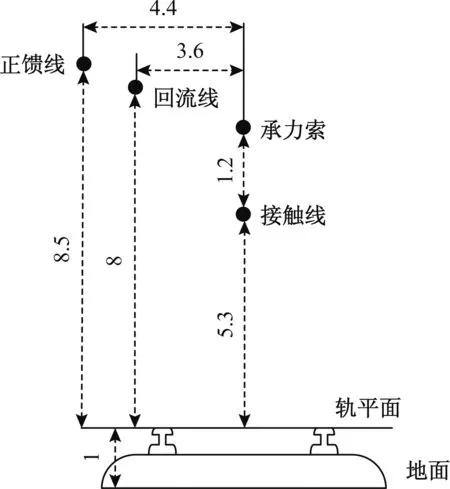
图1 牵引网悬挂系统几何结构(单位:m)
1.2 绝缘子闪络模型
绝缘子闪络过程的准确模拟无论是对反击还是绕击侵入波的计算都非常重要。本文采用电压控制开关的方法来模拟绝缘子的闪络过程,采用将绝缘子冲击放电的50%(记为U50%)与绝缘子伏-秒特性模型相结合的方式作为绝缘子的闪络判据,当绝缘子两端电压与其伏-秒特性曲线相交或两者不相交但是超过U50%时开关导通,绝缘子发生闪络放电[13]。在标准雷电波下绝缘子伏-秒特性为

(1)
式中:Vs-t为闪络电压,kV;L为绝缘子长度,m;t为从雷击开始到闪络所经历的时间,μs。
U50%采用文献 [10]中绝缘子雷电冲击放电试验获得的参数,见表1。考虑到大多数雷电为负极性,仿真中采用460 kV和315 kV分别作为T线和F线U50%判断值。

表1 接触网绝缘子雷电冲击50%放电电压 kV
1.3 车载氧化锌避雷器模型
避雷器模型主要在于模拟其非线性的伏-安特性曲线,仅用一个非线性元件不能完全模拟避雷器的动作过程[14]。文中采用IEEE工作组3.4.11提出的模型[15-17],见图2。已知动车组氧化锌避雷器的标称放电电流为10 kA,动作电压为60.5 kV,标准雷电冲击残压最大值为94 kV。
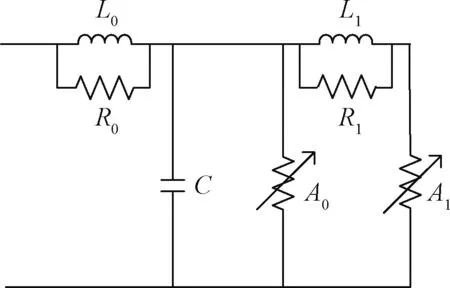
图2 避雷器模型
非线性电阻A0和A1可根据避雷器标准雷电冲击试验确定,其他参数均取决于该避雷器的几何尺寸,计算公式为
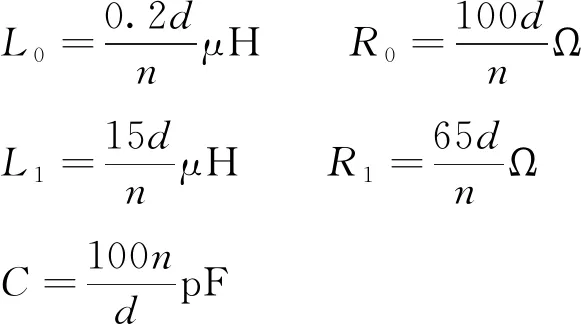
(2)
式中:d为避雷器元件的全长,m;n为并联柱数。计算可得L0=6.0 μH,C=250 pF,R0=40 Ω,L1=6.0 μH,R1=26 Ω。
1.4 冲击电晕模型
导线上雷击过电压大于导线的起晕电压时,在导线周围就会产生冲击电晕,电晕的产生引起导线对地电容和电导的增大。图3 为冲击电晕模型[18-19],K闭合时产生冲击电晕采用动态电导Gc和动态电容Cc来拟合冲击电晕的伏-库特性[20-21],动态电导用以表征冲击电晕引起的能量损耗,动态电容表征起晕后伏库特性曲线上升段非线性特点,两者均随导线电压变化。
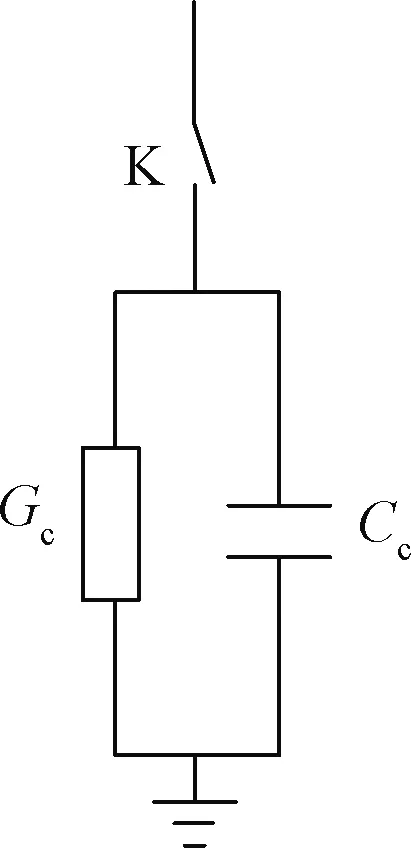
图3 冲击电晕模型
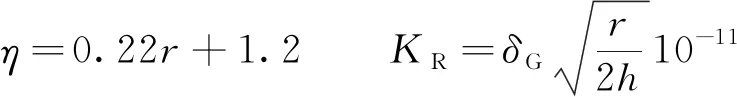
(3)
式中:C0为导线的几何电容;U和U0分别为导线电压和起晕电压;r和h分别为导线半径和对地高度;δG为电晕损耗常数。经计算,馈线的几何电容为6.827 pF/m,接触线和承力索的几何电容为14.252 pF/m。
2 牵引网-动车组仿真模型
现行规程中推荐的交流线路耐雷水平计算方法不考虑工作电压的影响,而且接触网电压等级较低,因此在模型中忽略接触网电压的作用。文中雷电流采用波形为2.6/50 μs的双指数波,对于雷电流的波过程,在大电流30~200 kA范围内波阻抗比较稳定,为600~300 Ω,取仿真中雷电通道波阻抗ZR=300 Ω,土壤电阻率为100 Ω·m。
由于雷电流为μs级别,等值频率约为1 MHz,此时变压器绕组为高阻性,杂散电容为低阻性,雷电压以电容分压的形式传递,变压器可用入口电容来等值[22]。仿真计算中,车载牵引变压器的入口电容设为500 pF,电压互感器的杂散电容设为100 pF[23]。
动车组主电路如图4所示,图中1号车(TC01)和8号车(TC08)为拖车,2号车(M02)和4号车(MH04)、5号车(MB05)和7号车(MB07)为动车,3号车(TP03)和6号车(TP06)为受电弓所在车。受电弓设在3号和6号车车顶,受电弓与车顶高压箱内设备通过高压电缆连接,断路器放置在车顶的高压设备箱内,车载变压器位于3号和6号车车底。受电弓端及断路器输出端分别设置一个避雷器。车顶高压电缆总长103 m,分布在3号车到6号车的4辆车车顶,电缆跨越车辆时,采用电缆终端连接,每段高压电缆的屏蔽层采用单端接地,变压器一次侧和主断路器也通过高压电缆连接。
仿真电路图及模型参数数值如图5和表2所示,模型中Rj为车体连接线电阻;Rd和Ld分别为接地电阻器电阻及其寄生电感;Rt为接地碳刷电阻;Rr和Lr为每节车体对应钢轨的电阻和电感值,单位长度钢轨电阻R=0.073 4 Ω/m,电感L=0.143 μH/m,已知首车车厢长度为25.86 m,其他车厢为24.83 m,将所有车厢均近似为25 m。

图5 雷击接触网时动车组过电压仿真模型

表2 仿真模型参数值
3 雷击T线(承力索/接触线)
由于接触线和承力索在每个跨距内都通过若干条吊弦相连接,在牵引网建模过程中,将承力索和接触线合并为二分裂导线。模型中考虑雷击T线绝缘子附近导线。图6为雷击接触网不同位置示意图,仿真过程中将不同幅值雷电流分别加载在和动车组不同距离的支柱附近,观察传播至动车组受电弓处的雷电流和变压器雷电过电压波形特征。
根据文献[24-25]推荐的雷电流幅值分布概率公式及观测数据,表3为幅值分别为60、80、100 kA雷电流雷击T线不同位置,经接触网传播至动车组受电弓位置的雷电流幅值大小。雷击T线后,由于雷电流较大,靠近雷击点的绝缘子发生闪络,大部分雷电流经由支柱流入大地,引起支柱电位的大幅度升高,并且由于支柱等值电感及接地电阻对雷电波的折、反射作用,支柱上的雷电过电压波形发生了振荡,振荡电压波作用在下一级T线绝缘子上,引起绝缘子的闪络放电。从表中可得,随着雷击点与动车组距离的增加,流经受电弓的雷电流幅值逐渐减小,在经过2~3级支柱后,传播至动车组受电弓处的雷电流幅值已经减小至10 kA以下,大约70%的雷电流在经过第一级支柱时流入大地。
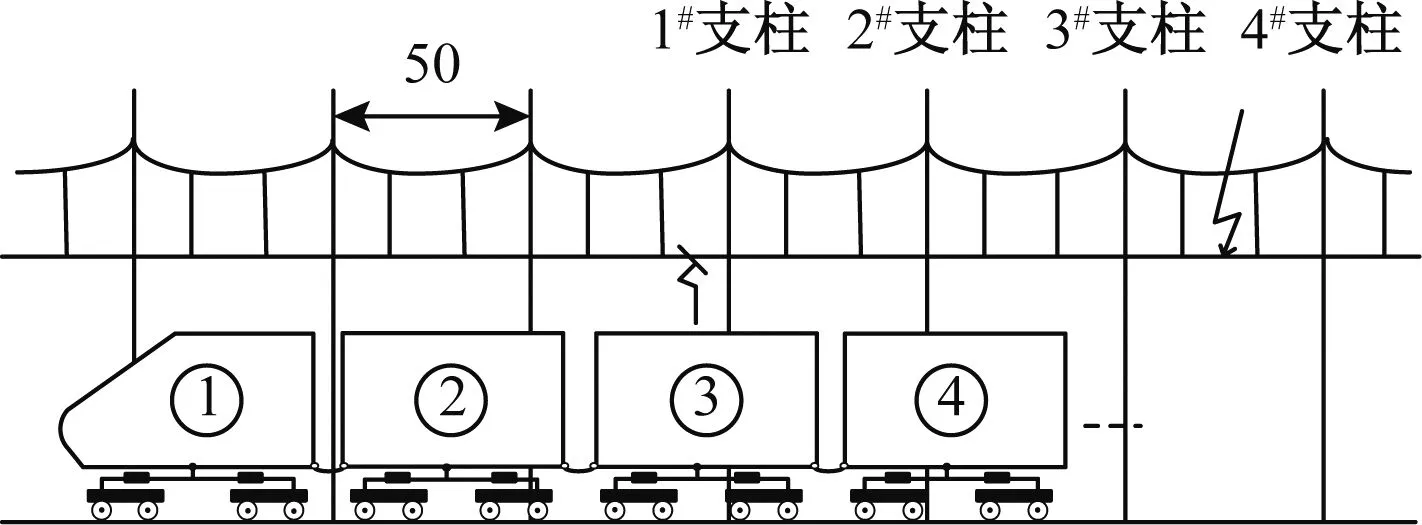
图6 雷击接触网位置示意图(单位:m)

表3 流经支柱的雷电流幅值 kA
近年来对变电站实际雷电侵入波的研究已经引起了关注,某变电站实测雷电侵入波具有50%统计概率的波前时间和波尾时间分别为20μs和198 μs,与目前用于测试变压器绝缘水平和试验研究的1.2/50 μs的标准雷电冲击波形区别较大[26-27]。研究结果表明,变压器油纸绝缘在实测雷电波和标准雷电波下的击穿特性存在明显差异,变压器绝缘配合方式还需考虑实测雷电数据[26]。为说明雷击接触网时传播至动车组高压系统的雷电侵入波特征,图7给出雷电流幅值为60 kA,雷击点与动车组不同距离时,流经受电弓的雷电流波形。可见动车组雷电侵入波与标准雷电流波形相比发生了衰减变形,其波前时间在10~20 μs,波尾时间在30~50 μs,这与雷电波在线路的传输过程、导线冲击电晕及避雷器等因素的影响有关。随着雷击点距离的增加,雷电流在传播过程中,幅值逐渐降低,波前时间逐渐增加,波尾时间逐渐减小。

图7 雷击点距离对受电弓处雷电流波形的影响
雷电冲击电压在沿接触网流向车顶高压设备时会触发避雷器动作,避雷器动作后,施加在距离避雷器较近的高压设备上的电压就成了避雷器动作后的残压。由于避雷器一般放置在车顶,其与车底变压器相距一定的距离,变压器入口电容和线路电感构成的LC回路引起侵入波的波前过程形成振荡[28],避雷器动作过后产生的电压波在变压器与避雷器之间发生多次折反射,变压器过电压值比避雷器的残压值要大。
图8为雷电流幅值为60 kA,雷击点在2#支柱和3#支柱之间时,车载避雷器动作后动车组避雷器和3号车及6号车变压器一次侧过电压波形图。可见,由于过电压折反射、避雷器电阻的衰减作用等,变压器波形相当于在避雷器残压上叠加一个衰减的振荡波,波前时间达到4.2 μs,大约在51 μs时过电压开始迅速衰减,经过50~60 μs减小至稳定值。3号车变压器一次侧过电压幅值为121.2 kV,6号车变压器一次侧过电压幅值为118.3 kV,过电压幅值大约为避雷器标称电流下残压值的1.3倍。

图8 动车组避雷器和3号车及6号车变压器一次侧过电压波形图
图9为避雷器标称放电电流下残压的比值范围。考虑到避雷器的正常工作范围,只给出雷击2#、3#和4#支柱附近时的比值大小,可以发现其值不大于1.34。
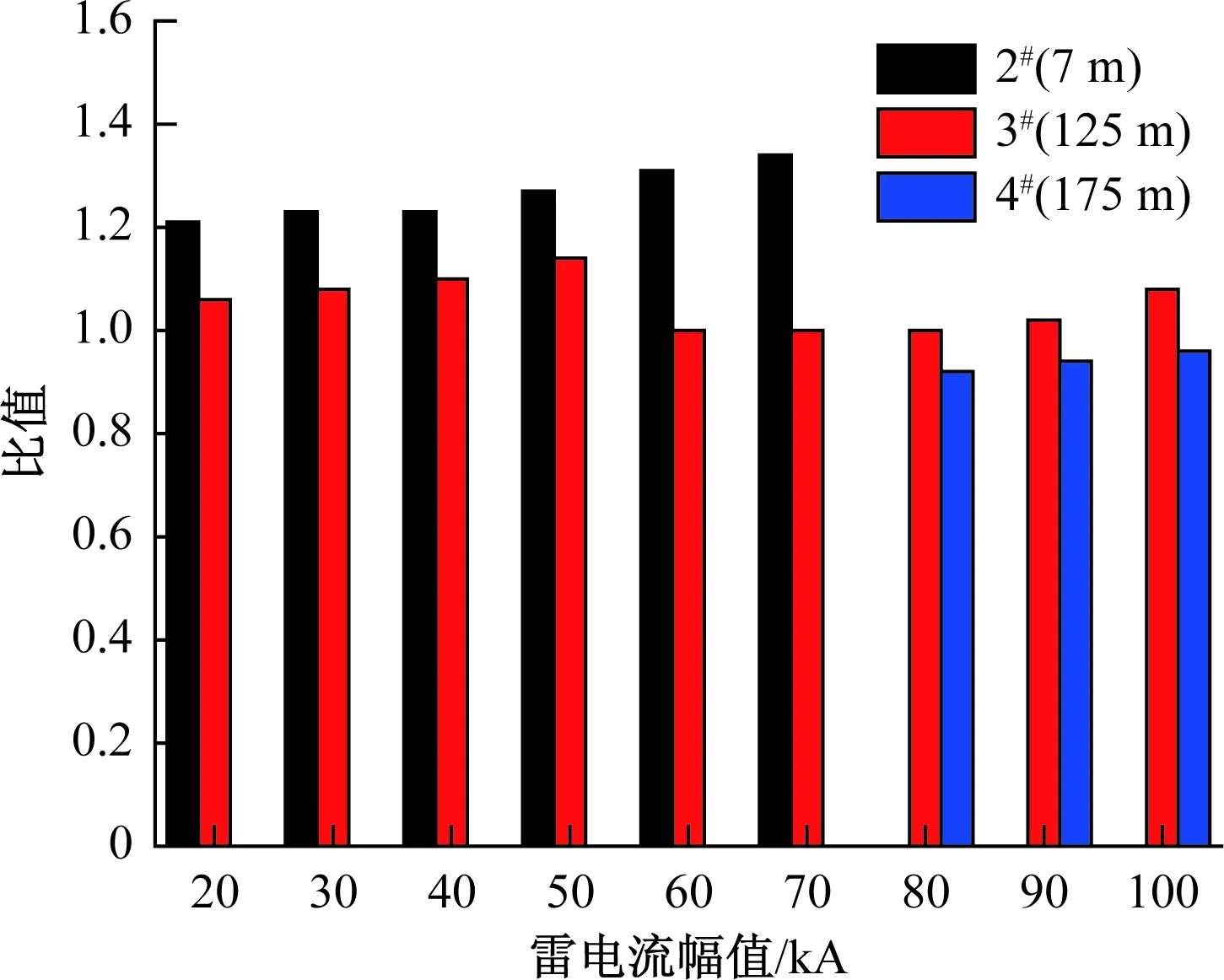
图9 车载变压器雷电过电压与避雷器保护水平比值
4 雷击F线(馈线)
雷击F线时,当馈线电压大于起晕电压时,起晕导线周围的空间电荷使导线间耦合电容增大,由于导线间的电磁耦合作用,在导线上将出现耦合电压。电晕引起的耦合电容Cij与电晕引起的导线对地电容Cc的比值为[29]
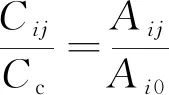
(4)
式中:

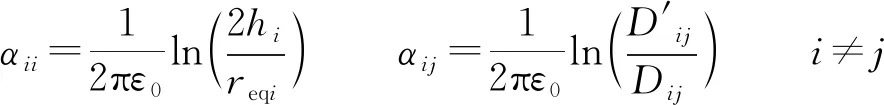
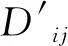
根据以上计算参数,可得接触网T线及F线电晕特性的非线性电路,见图10,其中C12为两线间耦合电容,K闭合时发生电晕。

图10 导线间电晕耦合电容
雷击F线时,F线绝缘子发生闪络,T线绝缘子未发生闪络。仿真过程中将不同幅值雷电流分别加载在馈线靠近支柱的位置,观察T线上感应电压波形和变压器雷电过电压波形特征。图11为T线上感应电压波形,其主要是由F线上的电位感应而来,波尾时间相较于标准雷电冲击波形有所减小,这主要是由于F线绝缘子闪络后,线路上雷电流迅速减小,T线上感应电压随之迅速衰减。T线上的感应电压形成后,将沿线路传播至动车组,受线路冲击电晕、电阻、电导等因素的影响,雷电感应电压波形在传输过程中发生衰减变形。分别计算雷击F线不同位置时沿接触线传播至受电弓处的电流幅值,如表4所示。可以发现,雷击F线后入侵动车组电流幅值在100 kA左右,随着雷击点距离的增加,受电弓处电流幅值逐渐减小。
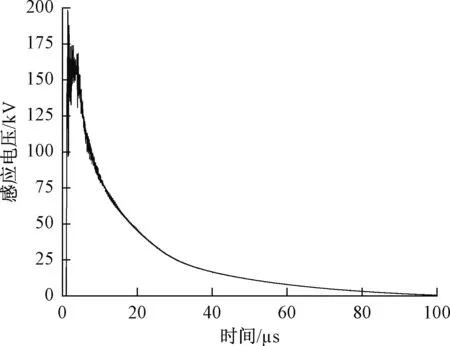
图11 T线感应电压

表4 流经支柱的电流幅值 kA
图12为雷电流幅值为80 kA,雷击点在1#支柱附近时,动车组避雷器和3号车及6号车变压器一次侧过电压波形图。可见3号车变压器一次侧过电压幅值为79.1 kV,6号车变压器一次侧过电压幅值为77.2 kV。由于避雷器对过电压的抑制作用,传播至动车组高压系统的感应雷电过电压将受到抑制,变压器过电压波形近似为平顶波,在波前位置形成振荡,波前时间达到6.3 μs,波尾时间相较于T线感应电压波尾时间有所减少,大约在28 μs时,过电压开始逐渐衰减至稳态值。

图12 动车组避雷器和3号车及6号车变压器一次侧过电压波形图
5 结论
(1)雷击T线(承力索/接触线)时,T线绝缘子发生闪络放电,动车组雷电侵入波波前时间在10~20 μs,波尾时间在30~50 μs。随着雷击点和动车组距离的增加,雷电波幅值逐渐降低,波前时间逐渐增加,波尾时间逐渐减小。
(2)不同幅值雷电流雷击T线不同位置时,车载变压器雷电过电压与避雷器保护水平的比值不大于1.34。变压器过电压波形相当于在避雷器残压上叠加一个衰减的振荡波,波前时间大于标准雷电冲击波前时间,波尾时间小于标准雷电冲击波尾时间。
(3)雷击F线时,馈线绝缘子闪络放电,线路上雷电流迅速减小,T线感应电压波尾时间小于标准雷电冲击波尾时间。受避雷器的工作特性的影响,车载变压器过电压波形近似为平顶波,波前位置出现振荡,波前时间大于标准雷电冲击波前时间,波尾时间相较于T线感应电压波尾时间有所减少。

