基于改进摩擦功模型的轮轨滚动接触磨耗研究

马超智，辛 涛,2,3，高 亮,2,3，崔旭浩

(1.北京交通大学 土木建筑工程学院,北京 100044；2. 北京交通大学 轨道工程北京市重点实验室,北京 100044；3.北京交通大学 北京市轨道交通线路工程与防灾工程技术研究中心,北京 100044)

车轮及钢轨的磨耗磨损成为影响铁路运输安全性及经济性的重大问题。文献[1-2]表明轮轨发生磨耗后,接触状态易由单点接触变为两点接触,并加速接触表面的磨耗伤损。为研究轮轨磨耗的作用机理,人们基于能量耗散磨损或黏着磨损理论对轮轨磨耗开展了大量的仿真研究。文献[3]以能量耗散磨损机制为理论基础,分析了摩擦系数对轮轨滚动接触磨耗的影响。文献[4]基于Zobory以能量流密度为基础建立的车轮磨耗模型,分析了压剪复合型弹性车轮的磨耗行为。文献[5-6]基于Archard磨损模型,建立轮轨型面磨耗的数值分析方法及磨耗演化过程。由于摩擦功等能量耗散模型以接触界面摩擦应力、相对滑动速度为参量,Archard磨耗模型以轮轨摩擦副较小的硬度值表征,故都无法分别表征轮轨介质各自的磨耗程度,不能很好反映不同屈服强度匹配时轮轨摩擦副的差异磨耗现象。

另外文献[7]对比分析了轮轨滚动接触的弹性及弹塑性解答,结果表明材料塑性变形改变了接触斑的黏滑分布范围。文献[8-9]通过扫描电镜发现轮轨接触表面多处产生明显的剪切塑性变形。文献[10]认为轮轨材料的抗磨损能力取决于材料抵抗塑性变形的能力。而材料进入塑性屈服状态后,抵抗塑性变形能力急剧降低,则抗磨损能力亦大幅降低。因此，材料的塑性屈服对接触磨损有显著影响,而既有的摩擦功指标主要关注接触界面的摩擦力、相对滑动速度,将接触斑滑动区范围内的塑性屈服区与非屈服区采用单一摩擦功指标进行整体考虑,无法细致反映材料塑性屈服对磨耗造成的影响,亦无法反映轮轨磨耗程度的差异。故需综合介质本身材料特性及摩擦磨损机理,对轮轨弹塑性滚动接触的磨耗机制做进一步研究。

本文针对传统轮轨磨耗模型无法关注接触处介质塑性屈服对接触磨损造成的影响,也不能很好反映不同屈服强度匹配时轮轨摩擦副的差异磨耗现象。依据摩擦功模型的能量耗散理论,通过Mises屈服准则对接触斑滑动区进行弹、塑性分区,并提出塑性区摩擦功(滑动区与塑性区交叠部分的摩擦功密度之和)的概念,以此表征接触处材料塑性屈服与滑动区摩擦磨损的共同作用。为进一步探索改进摩擦功模型的可行性,建立能考虑不同材料强度的三维轮轨滚动接触模型,将本文提出的轮轨塑性区摩擦功与接触斑总摩擦功进行综合分析,并进一步阐明其随轮轨屈服强度比的变化规律。

1 摩擦功模型改进

1.1 磨耗模型概述

接触磨耗模型主要分为两大类,一类以能量耗散为理论基础,主要有摩擦功模型或与磨耗指数有关的磨耗模型；另一类以黏着磨损为理论基础,且以Archard磨耗模型应用最广。

摩擦功模型认为磨耗仅发生在滑动区As，并且磨耗与摩擦功成正比[11]。任一单元格摩擦功(率)密度与Zobory模型的能量流密度计算公式相同,为

(1)

为衡量滚动接触时轮轨总体磨耗情况,可用接触斑内耗散的总能量近似表征,故取接触斑总摩擦功Wf为滑动区范围内各单元格摩擦功之和,计算公式为

(2)

Archard[12]认为,材料磨耗的体积Vwear与接触法向力、滑动距离成正比,与材料的硬度成反比,即

(3)

式中：k为磨耗系数,通过大量磨耗实验获得；Fn为接触法向压力；s为滑动距离；H为材料的硬度,取摩擦副的较小值。

1.2 磨耗分区及塑性区摩擦功的提出

轮轨材料是典型的弹塑性材料,借鉴文献[13],假定本构关系为双线性随动强化模型,见图1。通常材料的应力可表示为

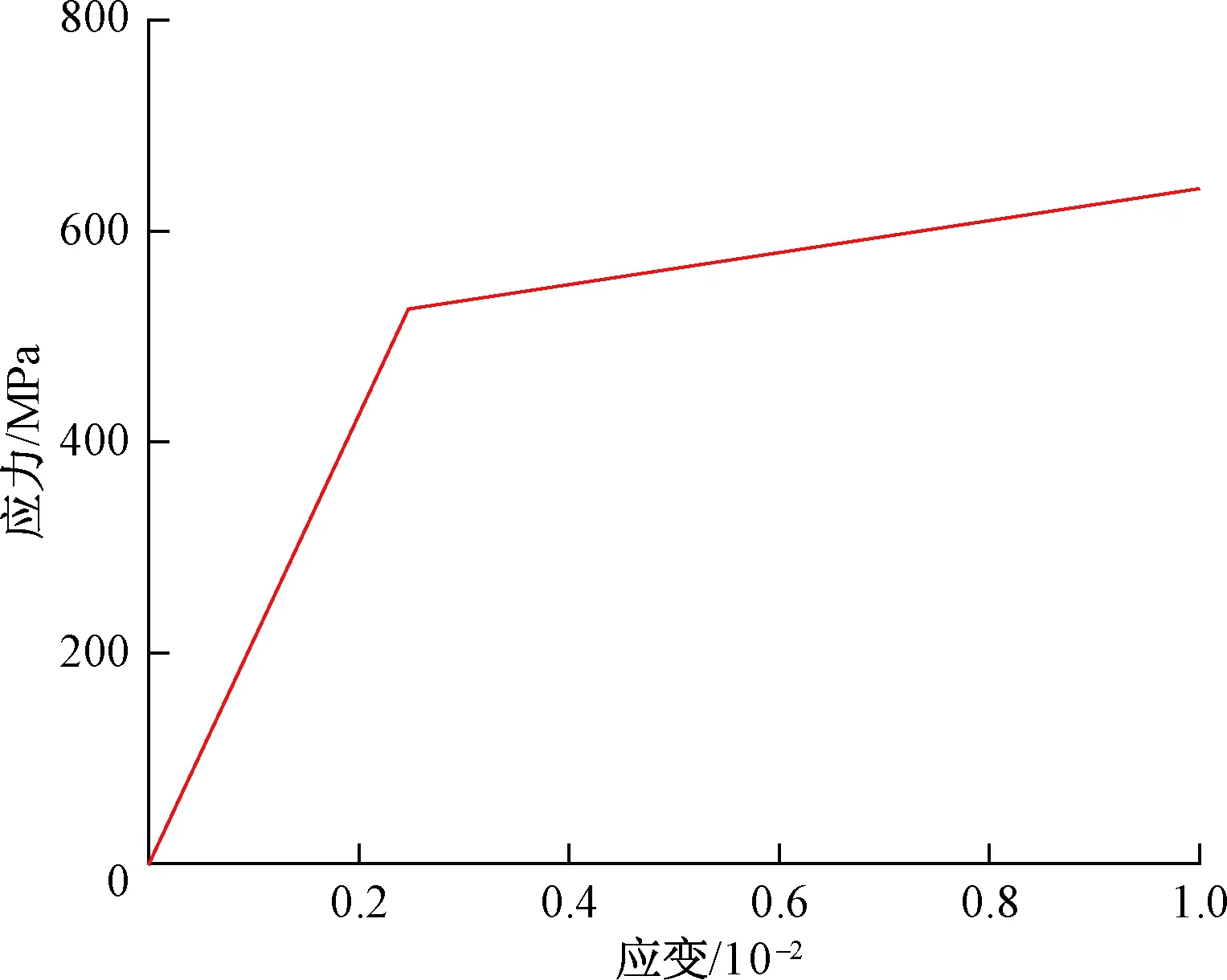
图1 轮轨弹塑性材料应力-应变曲线

式中：σ和ε分别为材料的应力和应变；σs和εs分别为塑性屈服点对应的应力和应变；Ee和Ep分别为弹性模量和塑性屈服后的强化模量。

当介质加载进入塑性屈服状态后,材料变软及抵抗变形能力大幅度降低,通过文献[10]可知,抵抗磨损的能力也显著降低,在加载条件下会大幅度增加磨耗程度。若磨耗只发生在滑动区的假设仍成立,当接触斑内塑性区与滑动区没有交叠时,即塑性区全部在黏着区内,则该塑性区内由于没有摩擦功的作用,故不会造成轮轨介质磨耗及显著的塑性流动变形；当接触斑内塑性区与滑动区有部分交叠时,交叠区范围内介质材料由于硬度、抵抗磨损能力显著降低以及轮轨间摩擦功的能量耗散作用,会加剧轮轨接触处介质的磨损并造成显著的塑性流动变形。

基于上述思路,材料塑性屈服后大幅度减小的抗磨损能力与接触斑滑动区摩擦功激扰的共同作用,会明显加剧摩擦副材料的磨损。故有必要将由黏着区及滑动区组成的接触斑[14]基于材料Mises屈服准则进一步细分为塑性黏着区、弹性黏着区、塑性滑动区以及弹性滑动区,见图2,并提取塑性区摩擦功,以此表征材料塑性屈服变软与摩擦功磨耗的共同作用。此外由于车轮、钢轨自身材料本构、接触几何形位的不同,轮轨接触斑内应力分布,以及依据Mises准则判定的塑性区分布也都不同,钢轨塑性区摩擦功不等于车轮塑性区摩擦功。故在应用塑性区摩擦功时,需先指明是车轮还是钢轨,这也表明了塑性区摩擦功这一评估指数可以反映轮轨磨耗程度的差异。

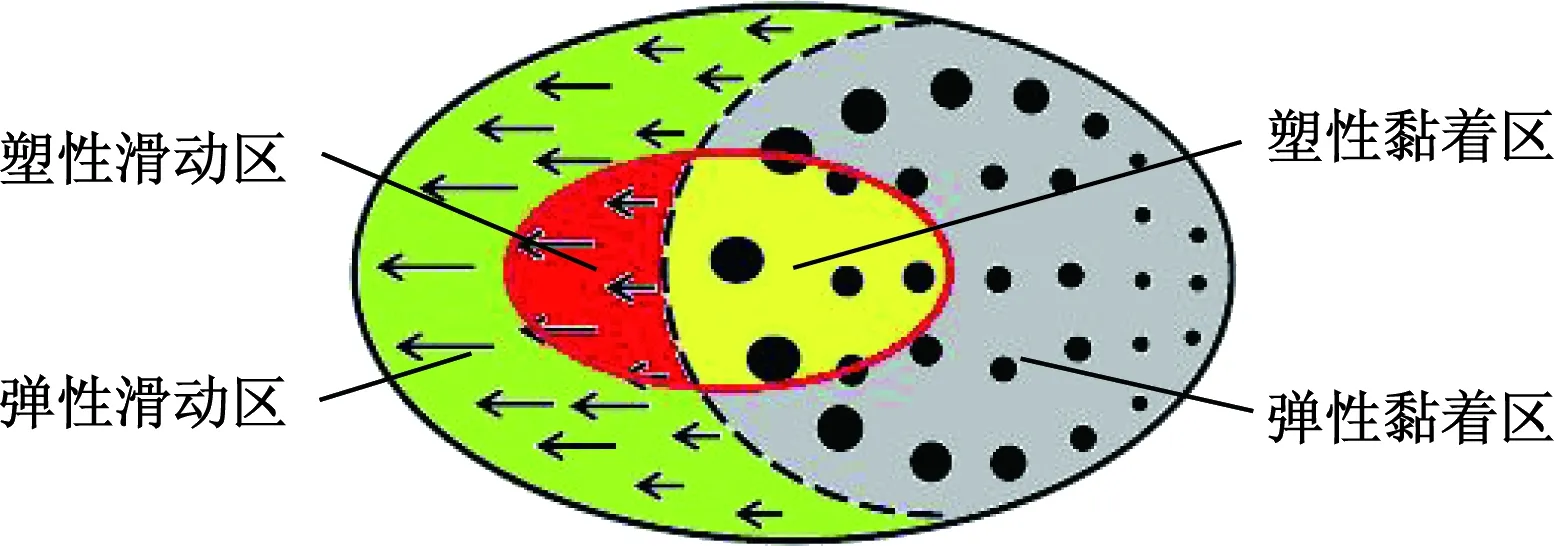
图2 基于材料塑性屈服的接触斑划分

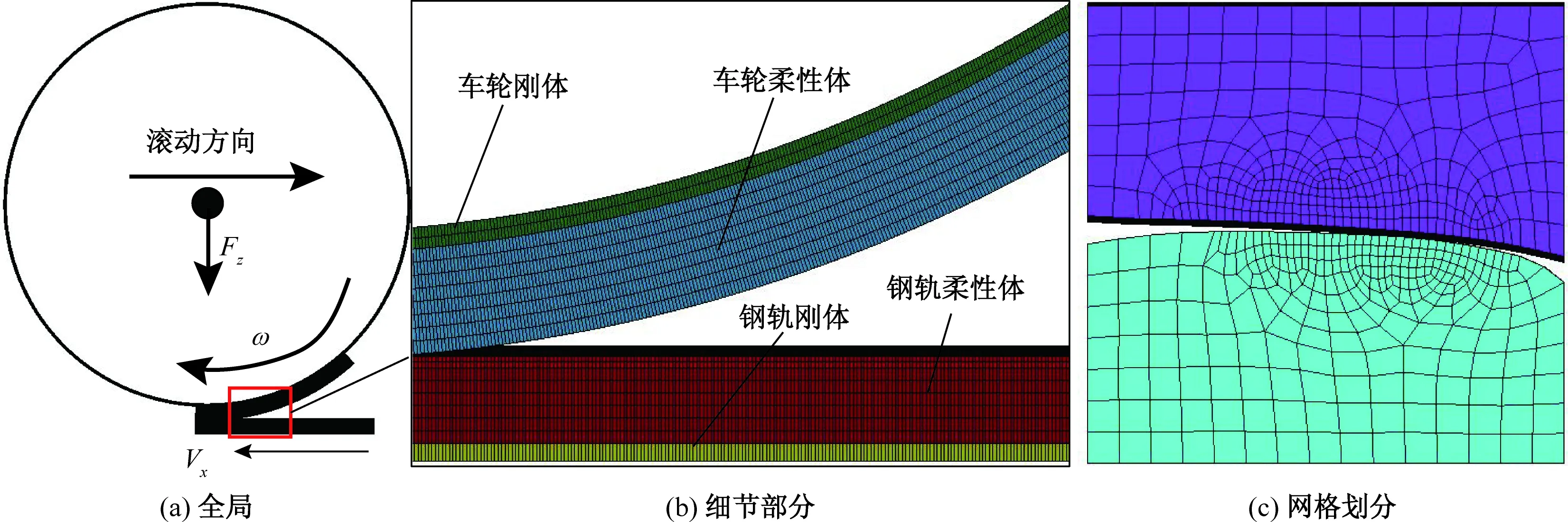
图3 轮轨滚动接触有限元模型

根据接触斑总摩擦功的计算方法,定义车轮(钢轨)塑性区摩擦功为摩擦功密度在车轮或钢轨接触斑塑性滑动区上的积分，即

(4)

若设未进入塑性屈服的滑动区为弹性滑动区,则接触斑总摩擦功可进一步表示为

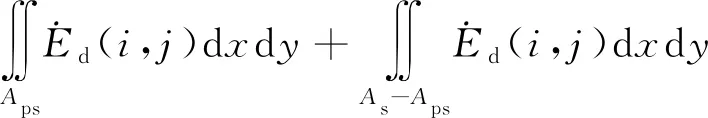
(5)

式中：Aps为车轮(钢轨)接触斑塑性区与滑动区的交叠区域(塑性滑动区)；Wpf为车轮(钢轨)塑性区摩擦功；Wef为车轮(钢轨)弹性区摩擦功。

根据上述定义,把塑性区摩擦功作为接触磨耗程度的衡量指标,其优点为:(1)可以考虑材料塑性屈服对摩擦副磨耗程度的影响；(2)能分别表征轮轨介质各自的磨耗程度,反映轮轨磨耗程度的差异。为研究改进磨耗模型的合理性及可行性,本文建立了弹塑性滚动接触有限元模型,以作进一步分析。

2 轮轨滚动接触模型

轮轨滚动接触有限元模型见图3,图中Fz为车轮载荷，ω为转速。为减少节点数量与计算成本,钢轨和车轮只取接触局域进行建模,通过试算车轮进入稳态滚动的时间,将钢轨和车轮柔性体长度取400 mm。由于弹塑性介质的阻尼耗能、窄带滤波作用,在远离接触点的部分,介质仅有很小的弹性变形[15],且该模型主要关注接触界面的复杂力学行为,因此本模型中轮轨柔性体垂向厚度各取30 mm即可保证很好的计算精度。此外为保证仿真结果能很好显示接触斑的形状,获得准确的接触应力分布,接触区域网格尺寸应足够小,结合文献[16-17],本模型接触区网格尺寸取为1 mm。为进一步减少整体网格数量并避免网格形状在某一方向尺寸超限而影响网格质量,对于轮轨非接触区网格尺寸最大为4 mm。

将对接触斑力学特性影响不大的部分设置为刚体,其中车轮刚体由轮心处的质点和与车轮柔性体绑定连接的环形刚体组成。采用这样的建模方法：一可以在不影响计算精度的同时显著缩短求解时间；二方便轮载集中力、滚滑速度的施加。本模型采用刚体驱动柔性体法来模拟车轮在钢轨上的滚动接触行为，滚滑速度设置方法如图3所示,即以施加钢轨刚体向左的平动速度Vx来模拟车轮向右的平动速度,同时施加车轮刚体绕车轴的转动速度ω,基于运动的合成法则即可模拟轮轨的滚动接触行为。为避免初始滚动、平动时刚体对柔性体造成的巨大冲击,降低轮轨系统的初始振荡,缩短进入平稳状态的时间,分别对车轮、钢轨柔性体施加与刚体相同的初始转动速度和平动速度。钢轨前、后截面施加非反射边界约束,以此消除反射应力波所造成的数值不稳定,同时对车轮刚体横向自由度、钢轨刚体垂向和横向自由度施加约束。平稳状态时,纵向蠕滑率为

(6)

式中：r为接触点的车轮滚动圆半径；ωr为接触点的转动速度。

轮轨接触面间的摩擦系数是影响磨耗的重要因素,采用面面自动接触和库伦摩擦准则来模拟轮轨接触界面的力学传递行为。为避免轮轨接触过程中不必要的数值振荡,垂直于接触表面的接触阻尼设置为临界阻尼的20%。库伦摩擦模型为[18]

(7)

式中：p为法向接触应力；τlim为动摩擦应力；fd、fs、DC分别为动摩擦系数、静摩擦系数、指数衰减系数；Vrel为轮轨相对滑动速度；τx、τy为纵横向切应力。本模型中fd=0.4,fs=0.4,DC=0；轮轨接触面摩擦系数μ取值为0.4[19]。

为进一步减小系统达到稳态的时间,将模型分两步进行求解。(1)添加人工阻尼并采用动态松弛法,求解得到静轮载作用下的位移场；(2)以位移场作为初始状态,施加与静轮载相同的轮载集中力、滚平动速度进行滚动接触仿真。图4为仿真得到的法向接触力fz、纵向蠕滑力fx时程曲线,在6.0 ms之后,轮轨滚动接触进入稳态。提取此时刻轮轨接触斑节点速度、接触法向、切向应力以及Mises应力等数据,确定接触斑滑动区、黏着区、塑性区分布范围以及摩擦功密度、接触斑总摩擦功、轮或轨塑性区摩擦功的数值。

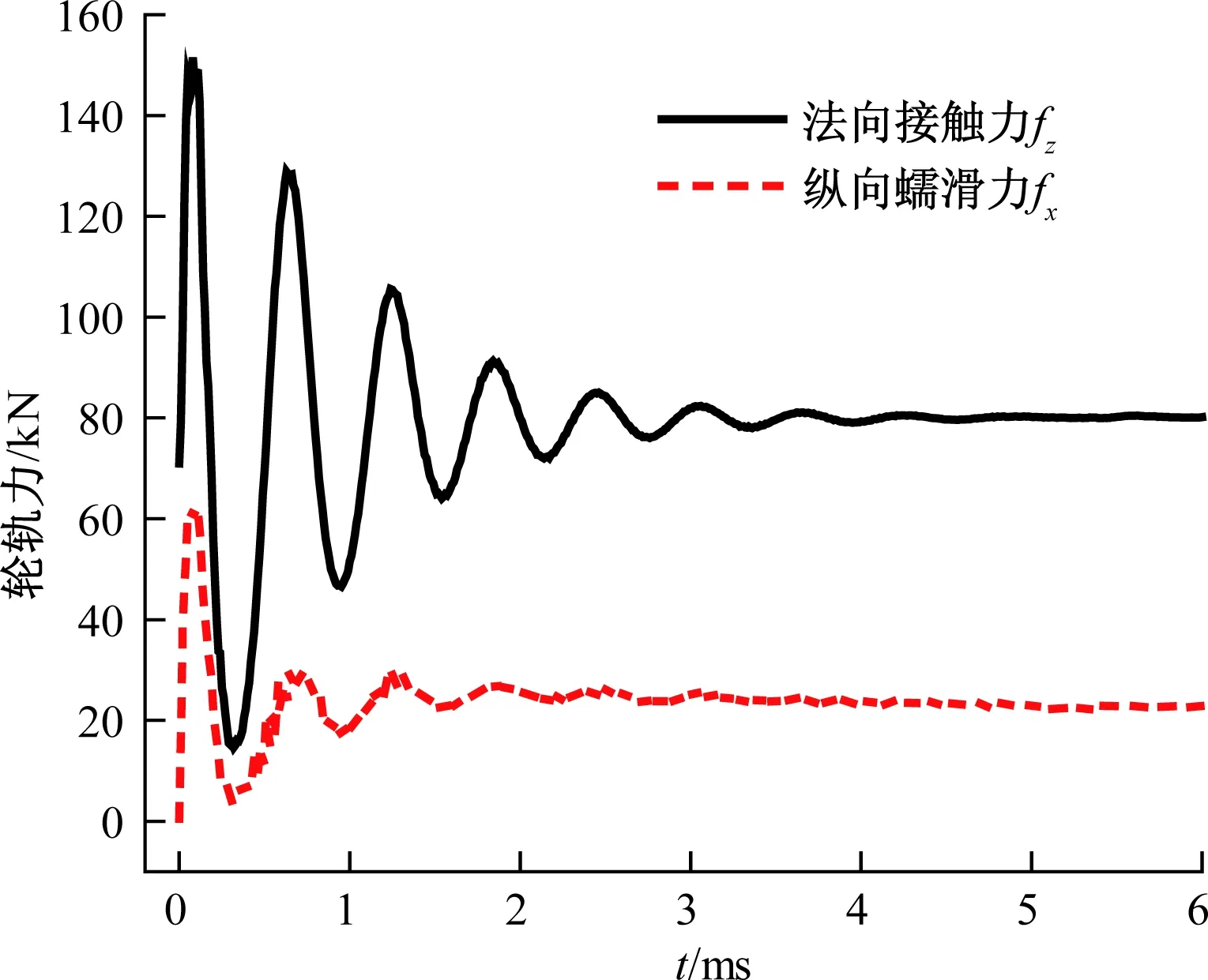
图4 法向接触力、纵向蠕滑力时程曲线

3 基于塑性区摩擦功的接触磨耗分析

3.1 算例

黏着系数会影响接触斑内滑动区的分布,进而影响塑性滑动区的分布以及塑性区摩擦功的数值。当车速小于300 km/h时,干态条件下轮轨黏着系数呈现无规律波动,并在0.2～0.4范围内无序变化[20],本文取黏着系数为0.28开展相关研究。以车轮屈服强度550 MPa、钢轨屈服强度500 MPa为例,分析车轮载荷80 kN、速度100 km/h以及黏着系数0.28时轮轨接触磨耗特征。基于接触节点力大于0、库伦摩擦准则以及Mises屈服准则,仿真得到车轮及钢轨接触斑黏滑、弹塑性分布见图5(图中X、Y为接触斑尺寸坐标),与图2基于材料塑性屈服的接触斑分区吻合,表明了改进摩擦功模型的可行性。由于车轮屈服强度是钢轨的1.1倍,钢轨接触斑与车轮接触斑塑性区分布不同,钢轨接触处介质有明显屈服而表现为较大塑性区,并与滑动区有交叠形成塑性滑动区；车轮材料屈服强度较高,接触时车轮表面只有小部分介质进入塑性屈服状态,且没有扩展延伸至滑动区,故不会形成塑性滑动区。基于此表明,当轮轨材料强度不同时,稳态滚动时虽然黏滑分布特征一致,但塑性滑动区却因轮轨屈服强度的不同而有显著差别。这也进一步表明改进的磨耗模型具有分别评价轮轨介质各自磨耗程度的优点。

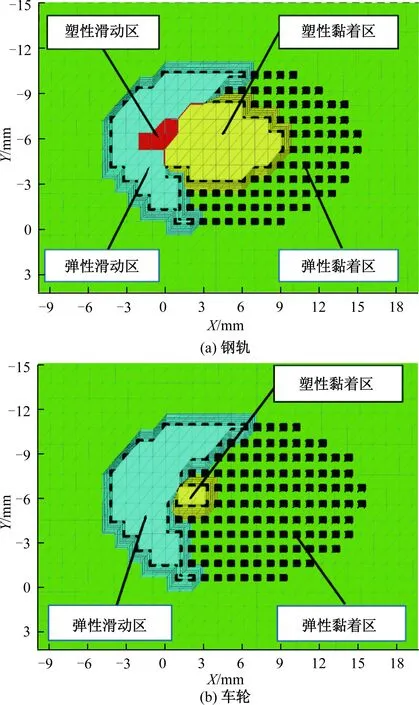
图5 钢轨和车轮表面黏滑及弹塑性分布

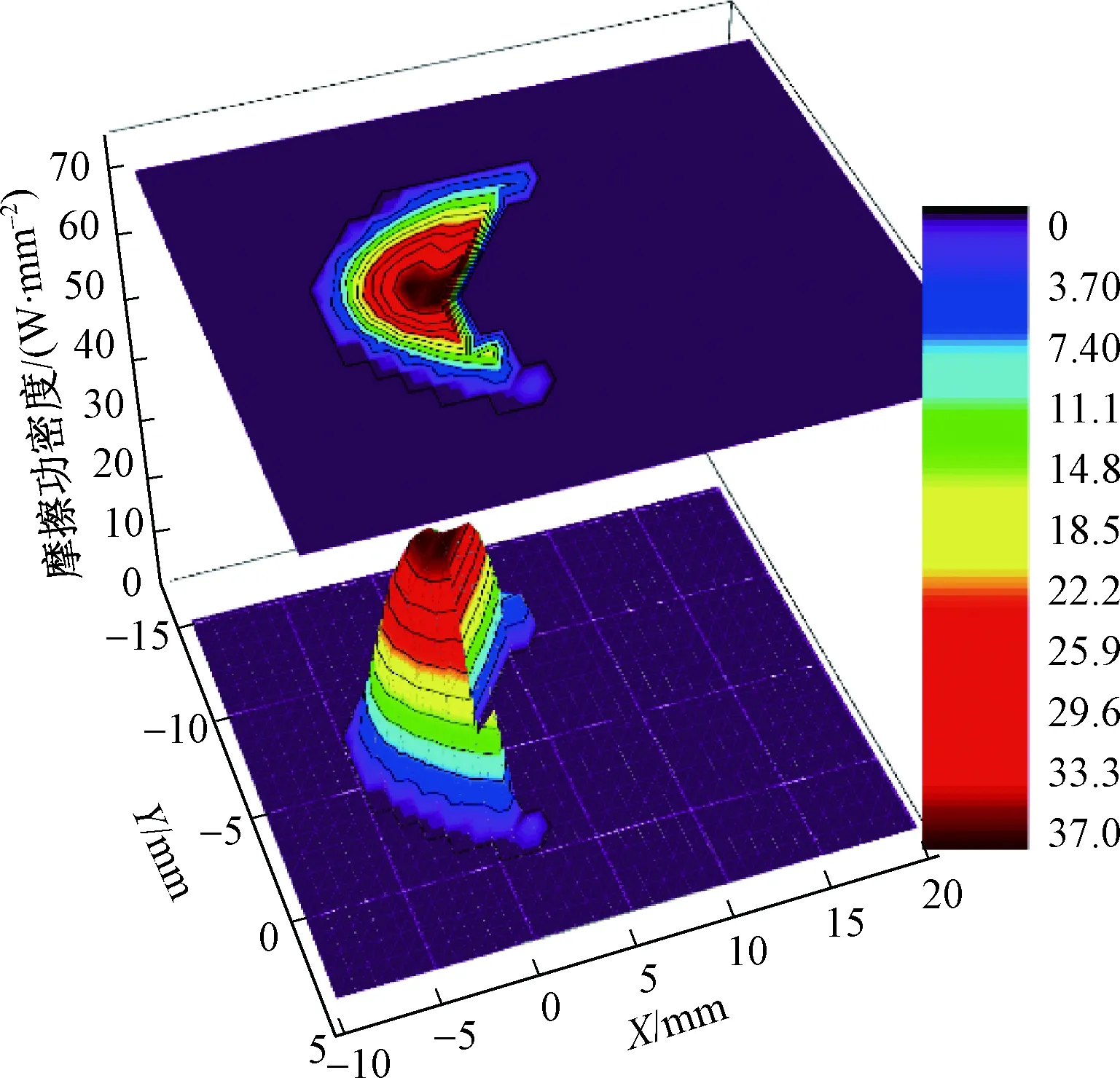
图6 接触斑摩擦功密度分布图

为进一步确定塑性区摩擦功、总摩擦功的数值,量化磨耗程度。图6给出了接触斑内摩擦功密度分布情况,由图可知,摩擦功密度分布呈明显的自旋效应,最大值为37.0 W/mm2,在滑动区内对摩擦功密度积分得接触斑总摩擦功为970.45 W,在钢轨塑性滑动区内对摩擦功密度积分得钢轨塑性区摩擦功为307.52 W,塑性区摩擦功为总摩擦功的31.69%。在车轮塑性滑动区内对摩擦功密度积分得车轮塑性区摩擦功为0,说明车轮接触斑滑动区与塑性区无交叠。当车轮屈服强度为550 MPa、钢轨为500 MPa,即车轮屈服强度高于钢轨时,车轮塑性区摩擦功小于钢轨塑性区摩擦功,得到车轮磨耗程度低于钢轨的结论,而这结论是接触斑总摩擦功反映不出的,显示出了塑性区摩擦功这一磨耗指标的优越性。

3.2 不同轮轨屈服强度的磨耗分析

我国铁路使用的轮轨材料多样，不同材料的屈服强度存在差异，目前合理的轮轨屈服强度比值仍存在较大争议。本节以提出的塑性区摩擦功以及总摩擦功为衡量磨耗程度的指标,分析轮轨屈服强度比在0.9～1.2范围内的磨耗变化规律，并探讨合理的轮轨屈服强度比值。此外,为明确材料塑性屈服对磨耗产生的影响,设置轮轨材料都为线弹性作对比分析；为揭示轮轨系统高、低屈服强度下磨耗的变化规律,设置轮轨屈服强度比为550 MPa/550 MPa作对比分析,共计11种工况,见表1。分析结果综合反映了塑性区摩擦功等评估指数随轮轨强度比值、大小等因素的变化规律。

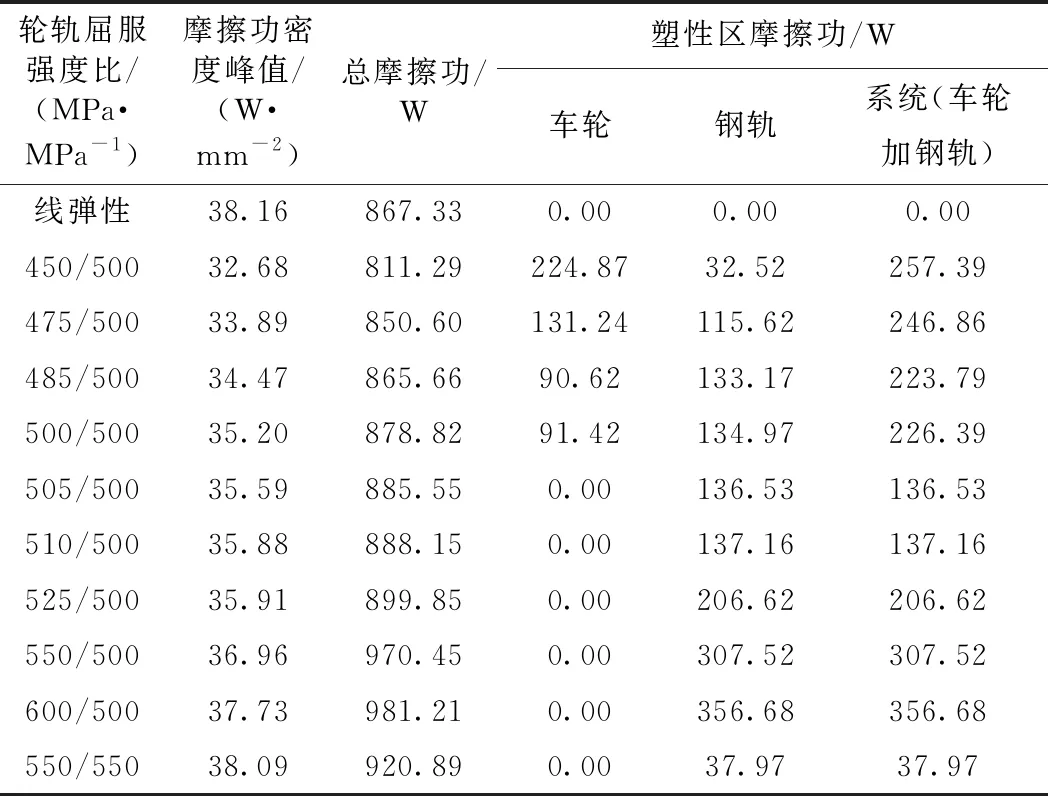
表1 不同轮轨屈服强度比下磨耗指标

保持钢轨屈服强度不变时,不同车轮屈服强度下的摩擦功与塑性区摩擦功变化规律见图7。从分析改进模型及传统摩擦功模型可得如下结论:

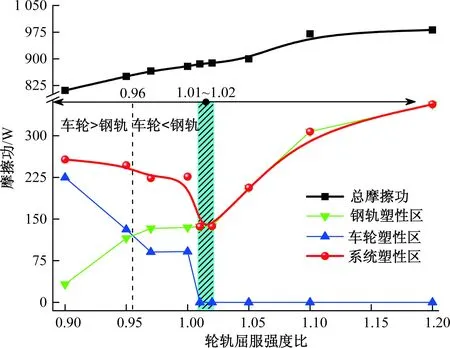
图7 摩擦功与塑性区摩擦功随轮轨屈服强度比变化曲线

(1)基于改进摩擦功模型(由塑性区摩擦功表征):

①相同钢轨屈服强度下,提高车轮屈服强度使钢轨塑性区摩擦功增大,即钢轨磨耗程度增大；而车轮塑性区摩擦功则先减小后保持不变,即车轮磨耗程度先减小后变化不明显。该结论与文献[21]基于3种材质车轮与3种材质钢轨的对磨试验得到的测试结果是一致的。

②车轮及钢轨塑性区摩擦功之和(系统塑性区摩擦功)变动显著,并呈先减小后增大的趋势。文献[22]基于摩擦磨损试验表明,随着轮轨硬度(强度)比的提高,轮轨系统的磨损量呈现先减小后增大的趋势,改进摩擦功模型反映的结论与试验测试结果基本吻合。

(2)基于传统摩擦功模型(由总摩擦功表征):随着轮轨屈服强度比的提高,总摩擦功缓慢增大,轮轨磨耗程度均逐渐增大。传统摩擦功模型反映的磨耗规律与文献[22]的试验结果有一定偏差。

对比改进及传统摩擦功模型得到的结论,发现改进摩擦功模型与轮轨摩擦磨损试验得到的结果基本相符,且还可根据车轮塑性区摩擦功、钢轨塑性区摩擦功的相对大小来衡量轮轨磨耗的相对高低,反映轮轨磨耗程度的差异,所能反映的轮轨磨耗特征信息更合理、丰富；而传统摩擦功模型仅采用单一的总摩擦功为轮轨磨耗评判指标,所能反映的轮轨磨耗特征信息较少,无法体现轮轨磨耗程度差异。

(3)依据表1及图7,还可得到如下结论:

①弹塑性材料的摩擦功密度峰值低于线弹性材料,分析原因主要是轮轨接触处介质进入塑性屈服后,造成接触应力重分布,进而降低接触应力集中程度,使得接触斑摩擦功密度分布趋向均匀。

②轮轨屈服强度比小于0.96时,车轮塑性区摩擦功大于钢轨塑性区摩擦功,车轮磨耗程度高于钢轨；轮轨屈服强度比为1.01～1.02时,系统塑性区摩擦功降到最小,由于总摩擦功在屈服强度比0.9～1.2范围内增幅不明显,磨耗程度近似可由塑性区摩擦功衡量,基于此轮轨屈服强度比控制在1.01～1.02时,有利于减小系统磨耗；轮轨屈服强度比大于1.01时,车轮塑性区摩擦功减小到0,表明车轮接触斑内滑动区未与塑性区发生交叠,即车轮接触斑磨耗区(滑动区)范围内材料未进入塑性屈服状态,此时车轮磨耗程度则应由总摩擦功衡量。

③轮轨屈服强度均为500 MPa或550 MPa,这两组数据表明,轮轨屈服强度相同时钢轨塑性区摩擦功均高于车轮,说明接触处钢轨介质比车轮介质更容易进入塑性屈服状态,以及钢轨比车轮更易产生磨耗,分析原因可能是由于车轮踏面锥度以及轨底坡等接触几何形位造成的。

④在保证轮轨屈服强度比不变的情况下,整体提高屈服强度,接触斑总摩擦功稍微增大,但车轮或钢轨塑性区摩擦功显著减小。如当轮轨屈服强度由500 MPa提高至550 MPa时,总摩擦功增大4.8%,系统塑性区摩擦功减小83.2%,钢轨塑性区摩擦功减小71.9%,车轮塑性区摩擦功减小至0,表明整体提高轮轨屈服强度,对减少系统磨耗有积极意义。

4 结论

本文基于既有能量耗散磨损理论,通过考虑轮轨接触时材料塑性屈服对磨耗造成的影响,提出了弹、塑性分区磨耗分析方法及塑性区摩擦功这一评估指数。进一步建立了可考虑轮轨材料不同屈服强度比的滚动接触模型,仿真分析了塑性区摩擦功、总摩擦功随轮轨屈服强度比的变化规律,探讨了轮轨合理的屈服强度匹配。主要结论为：

(1)相比总摩擦功,塑性区摩擦功既可考虑材料塑性屈服后抗磨损能力降低对轮轨磨耗的影响，也能分别表征轮轨各自的磨耗程度,反映轮轨磨耗的差异，体现了塑性区摩擦功这一评估指数的优越性。

(2)相同钢轨屈服强度下,提高车轮屈服强度使钢轨塑性区摩擦功增大,即钢轨磨耗程度增大，而车轮塑性区摩擦功则先减小后保持不变,即车轮磨耗程度先减小后变化不明显。

(3)随着轮轨屈服强度比的提高,接触斑总摩擦功缓慢增大,车轮及钢轨塑性区摩擦功之和变动显著,并呈先减小后增大的趋势。系统塑性区摩擦功随轮轨屈服强度比的变化规律与试验结果体现了很好的一致性。

(4)轮轨屈服强度比小于0.96时,车轮塑性区摩擦功大于钢轨,车轮磨耗高于钢轨；轮轨屈服强度比为1.01～1.02时,系统塑性区摩擦功降到最小,有利于减小系统磨耗。由于车轮踏面锥度及轨底坡等接触几何形位的影响,轮轨同强度时接触处钢轨介质比车轮介质更容易进入塑性屈服状态以及钢轨比车轮更易产生磨耗。

(5)在保证轮轨屈服强度比不变的情况下,整体提高屈服强度,接触斑总摩擦功稍微增大,轮或轨塑性区摩擦功均显著减小,基于此整体提高屈服强度对降低轮轨系统磨耗有积极意义。