高空长航时无人机螺旋桨后掠桨叶气动研究

马成宇,何国毅,王 琦

(南昌航空大学 飞行器工程学院,南昌 330063)

0 引 言

螺旋桨是指通过桨叶旋转推动气流加速运动从而产生推力的动力装置。在喷气动力之前,螺旋桨是航空飞行器的主要动力系统,即便在世界航空史进入喷气动力时代之后,螺旋桨以其高效、经济的优势依然是部分航空飞行器首选的动力装置[1-2]。但由于螺旋桨桨尖马赫数的限制,传统的螺旋桨无法在高亚音速范围内高效工作,因此对于螺旋桨的应用及设计很长时间只停留在低速范围内。为提高螺旋桨的桨尖临界马赫数,早在20世纪50年代,桨尖后掠的螺旋桨桨叶就已出现[3],20世纪70年代美国率先开展了先进螺旋桨计划,从气动、结构、噪声等方面对后掠桨叶进行设计和计算[4-6],法国,英国等欧洲各国相继开展高速螺旋桨的研究,前苏联也取得显著的成果,乌克兰D-27发动机上所安装的桨叶是后掠桨叶实际应用的典范[7-8]。到目前为止,多数投入使用的螺旋桨都考虑到了后掠设计,但由于对飞行速度没有过高要求,所设计的螺旋桨桨叶只是轻微的后掠,同时由于当前使用涡扇发动机执行高速飞行任务所用成本在可接受范围之内,因此对螺旋桨高速性能的研究鲜有报道。

近年来,随着人类对空域的不断探索,高空长航时无人机逐渐成为各国研究热点。高空长航时无人机是指飞行高度不低于18 km,飞行时间不少于24h的战术或战略无人机[9],相对于轨道卫星,其成本较低,可随时更改航线,机动性强,且飞行高度较低,侦察图像分辨率高,可广泛应用于空中预警、通信中继、电子干扰、拦截战区弹道导弹、海岸与边界巡逻、大气环境研究和空中交通管制等,被人们称为“大气层人造卫星”[10-11]。根据其任务要求,高空长航时无人机对能量来源和推进系统有较高要求:首先,长航时的设计要求,使得无人机的供能系统必须能够长时间地供应能量,同时推进系统必须具有较高的经济性以减少能量消耗;其次,无人机要爬升到一定高度执行任务,要求推进系统能够保证无人机具有良好的爬升能力[12],尽量缩短爬升时间;此外,由于无人机的任务航线可随时更改,这就要求无人机具有较好的机动能力,可以很快到达指定的任务区域,到达指定区域后又能以较低的飞行速度执行侦察、监视等任务,因此推进系统还需具备宽工况的特性。高空长航时无人机按照能量来源的不同可以分为:常规动力无人机、太阳能动力无人机、氢动力无人机和混合动力无人机。其中常规动力无人机通常选用燃油动力或者化学电池电动系统,难以满足长航时的设计要求;而太阳能动力无人机通常采用超大展弦比轻质结构[13-14],同时受限于天阳能转化率低的限制,只能够低速续航,无法满足快速机动的设计要求;氢动力无人机因航空用燃料电池具有转化率高、功重比高和能量密度大等特点[15-17],同时在结构设计方面与太阳能动力无人机相比不需要超大展弦比设计,使得无人机结构较强,可以达到较高的飞行速度[18];此外,采用氢能/太阳能混合动力作为供能系统,综合两者供能方式的长处,是最有潜力满足长航时和宽工况设计要求的供能系统[19-20]。对于推进系统的选择,螺旋桨因其在低速范围内的高效性可作为高空长航时无人机的推进系统,以满足高空长航时无人机慢速飞行对某一特定目标进行监视和细节辨认的要求,同时由于螺旋桨的经济性,易于无人机长航时飞行。唯一不足的是螺旋桨高速性能不佳,同时考虑到高空空气稀薄,不利于散热,高空无人机一般采用传动结构较为简单的定距螺旋桨[21],当飞行速度在偏离设计点之后螺旋桨效率下降很快。

目前国内外的专家学者对高空无人机螺旋桨的研究主要集中在抑制桨叶气流分离[22-25]、螺旋桨与机翼气动干扰[26-27]以及在设计飞行速度下螺旋桨桨叶设计[28-29]三个方面,而对如何加宽螺旋桨的有效工作范围,增强快速爬升和机动能力研究甚少,因此针对这一问题,本文将桨叶后掠的设计思想应用到高空长航时无人机螺旋桨的改进设计上,探究桨叶后掠角对螺旋桨气动性能的影响规律,研究结论同样对工作于传统高度内的螺旋桨提高其高速性能具有借鉴和指导意义。

1 桨叶物理模型说明

1.1 桨叶建模方法说明

本文所用无后掠桨叶数据取自文献[11],螺旋桨半径2.3 m,设计巡航马赫数为0.4,基本叶素翼型为Eppler387。以笛卡尔坐标系的z轴为叶素积叠线,沿展向分布10个叶素,不同展长处叶素的弦长中点布置在z轴上,叶素弦长分布和扭转角分布见文献[11],最终形成的无后掠桨叶见图1。

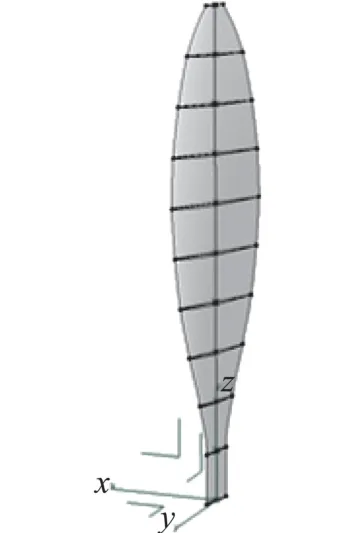
图1 无后掠桨叶示意图Fig.1 Unswept-blade model

后掠桨叶在无后掠桨叶的基础上进行改动,见图2:首先将无后掠桨叶各个叶素的弦线前后延长形成和桨叶扭转角一致的扭转面,其次在无后掠桨叶积叠线的一半处将积叠线分成上下两部分,上半部分积叠线沿着y方向后掠β角度,并延长上半部分积叠线使得后掠后的顶点z坐标和无后掠桨叶积叠线顶点z坐标相同,形成后掠积叠折线,再将后掠积叠折现绕z轴旋转任意角度使得旋转面和扭转面相交,然后通过相交线的顶点、无后掠积叠线中点和起点形成一条样条曲线,将此样条曲线投影到扭转面上即形成后掠积叠曲线,最后按照无后掠桨叶的弦长分布和扭转角分布在后掠积叠曲线上平均分布10个叶素形成后掠角为β的后掠桨叶。为保证后掠桨叶和无后掠桨叶的表面积近似相等,建模时近似认为桨叶在扭转面上的投影相等则桨叶表面积相等。无后掠桨叶和后掠桨叶在扭转平面上的投影可近似看成梯形,梯形的上底和下底相同(半展长处和桨尖处叶素弦长相同),要保证梯形面积不变,则要求梯形的高相同,因此要求后掠桨叶积叠线顶点z坐标和无后掠桨叶积叠线顶点z坐标相同。最终形成的无后掠桨叶表面积为1.47 m2,最大后掠50°时桨叶表面积1.491 m2,误差为1.42%,在可接受的范围。

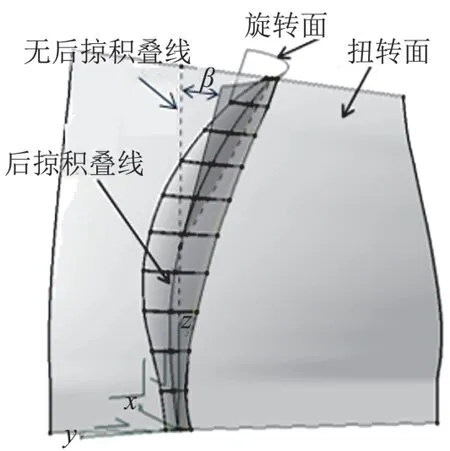
图2 后掠桨叶建模示意图Fig.2 Swept-blade model

1.2 螺旋桨半径及转速确定方法说明

半径是螺旋桨设计的重要参数,直接影响到螺旋桨转速的确定。无后掠桨叶的半径为叶素积叠线的长度,后掠桨叶的半径为后掠积叠线起点和顶点所连空间线段在垂直于平飞方向的平面上的投影,因为无后掠桨叶的积叠线起点和终点所连空间线段在垂直于平飞方向的平面上的投影就是积叠线本身,可见无后掠桨叶是后掠桨叶的特殊情况。为避免螺旋桨桨尖激波阻力的影响,本文要求所有后掠桨叶在相同的前飞速度时桨尖马赫数相等,即所有桨叶的桨尖切向速度(2πNsR,Ns表示螺旋桨转速,R为螺旋桨半径)相同,因此根据无后掠桨叶螺旋桨的半径(2.3 m)和转速(860 r/min)以及各个后掠桨叶螺旋桨的半径即可确定后掠桨叶螺旋桨的转速,所有后掠桨叶螺旋桨的转速和半径均列于表1。

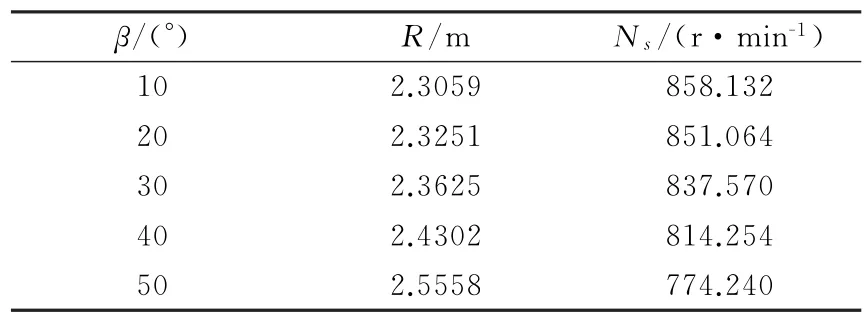
表1 后掠桨叶旋转半径和转速Table 1 Rotation speed and radius of different propellers

2 数值方法与验证

2.1 数值模拟方法与网格无关性验证

本文所用螺旋桨的工作高度为25.9 km,此高度的大气物理属性如下:大气压强p＝2549.2 Pa,大气密度ρ＝0.034 75 kg/m3,黏度μ＝1.46×10-5kg/(m·s),温度T＝221.5 K,导热系数λ＝1013 J/(kg·k)。数值模拟采用商用CFD软件STAR-CCM＋完成,基于笛卡尔网格和周期性边界条件仅对单个桨叶进行计算。计算域分为旋转区域和静止区域两部分(图3),考虑到桨尖空气压缩性影响,对桨尖区域局部加密,桨叶附近网格见图4。采用多重参考系模型定常求解雷诺时均N-S方程和Realizable k-ε湍流模型,空间离散方法采用二阶迎风插值的Roe格式。对无后掠桨叶进行网格无关性验证,此时螺旋桨的工作状态为:转速Ns＝860 r/min,来流速度v0＝112.13 m/s,分别改变桨叶表面面网格尺寸为10 mm、7 mm、5 mm、3 mm,对应的体网格数量为:1075万、1100万、1324万、1390万。图5为螺旋桨拉力T和力矩M的网格无关性曲线图,当桨叶面网格尺寸小于5 mm(体网格1324万)之后,计算所得拉力和力矩的波动已经很小,故对无后掠桨叶和后掠桨叶的计算均采用5 mm的桨叶面网格。

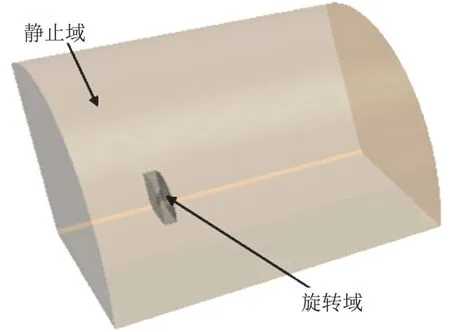
图3 计算域示意图Fig.3 Computational domain

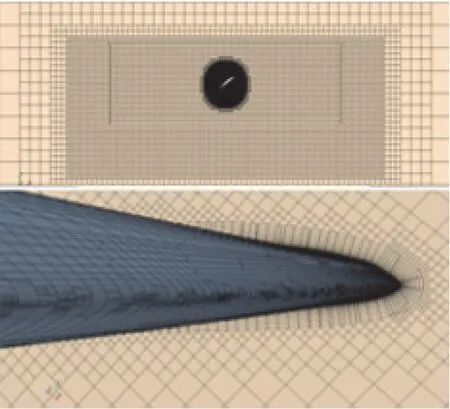
图4 桨叶附近网格Fig.4 Mesh around the blade

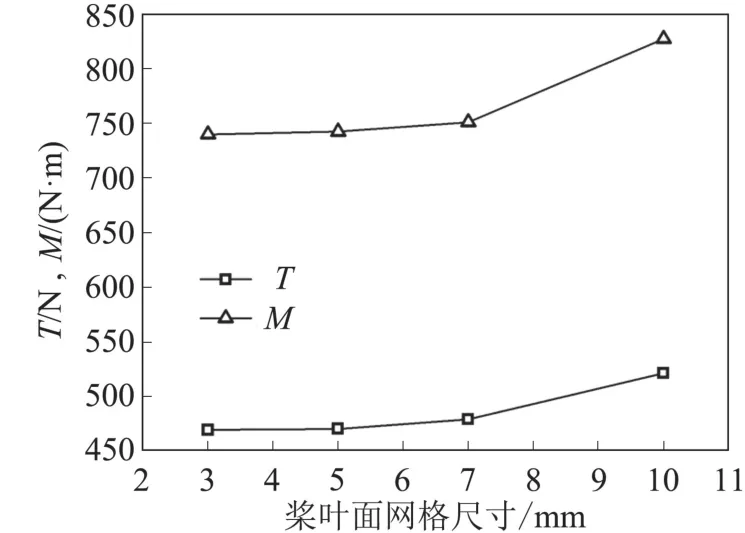
图5 网格无关性验证Fig.5 Mesh independency study

2.2 无后掠桨叶螺旋桨计算结果校核

工程上除采用数值模拟方法计算螺旋桨气动性能外,也常采用片条理论计算螺旋桨气动性能。因此采用第2节所述数值方法,计算了无后掠桨叶从设计点(进距比J＝1.7,对应的巡航速度为112.13 m/s)到进距比为2.3(巡航速度151.71 m/s)的拉力系数Ct和力矩系数Cm,在图6中与文献[11]中片条理论计算结果进行了对比,可见两种方法得到的拉力系数和力矩系数随进距比增大的变化趋势吻合,其中数值模拟方法计算结果比片条理论计算结果略大。在文献[30]中也有类似的结论。因此可以认为本文所用的数值模拟方法满足当前阶段的计算精度和要求,可用于初步探究后掠桨叶的气动变化规律。

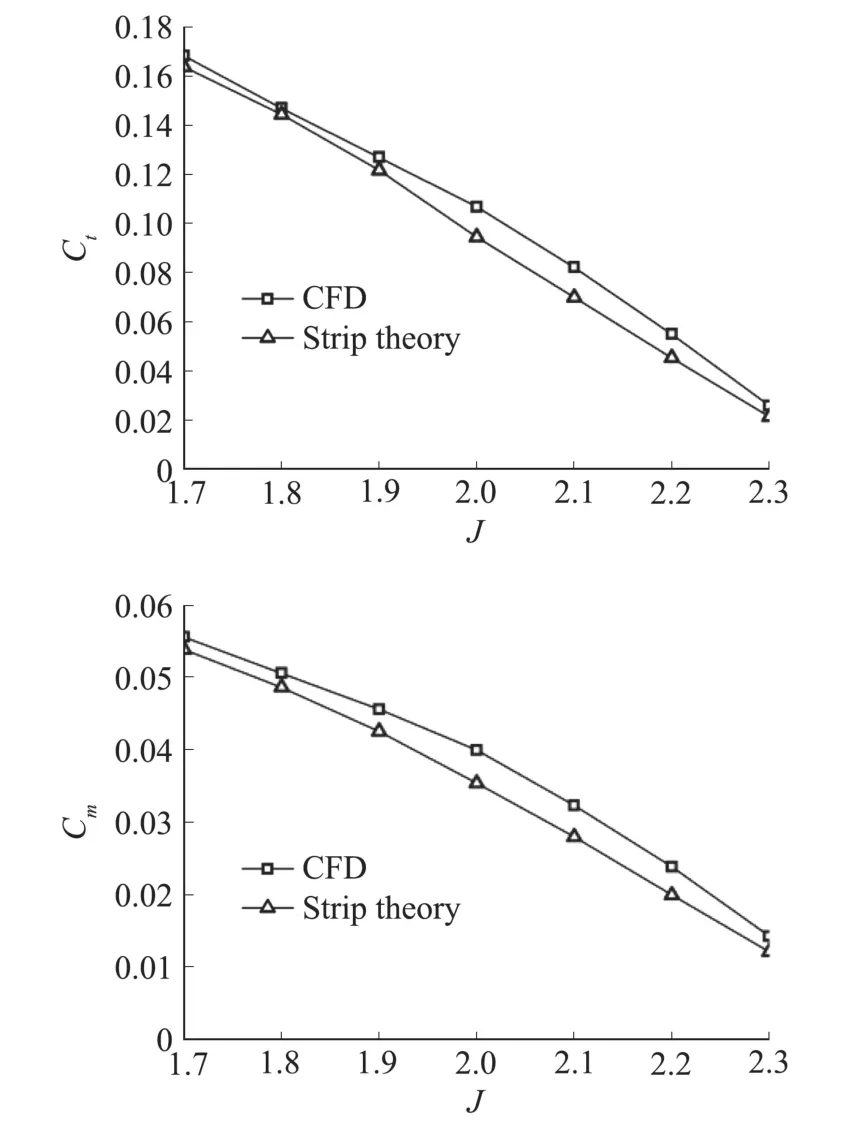
图6 无后掠桨叶片条理论与数值计算结果对比Fig.6 Comparison between strip theory method and CFD method

3 无后掠桨叶螺旋桨气动性能分析

图7为进距比从1.7到2.3范围内无后掠螺旋桨性能曲线。随着进距比增大,拉力系数和功率系数CW均下降,效率η经过一段缓慢增加之后急剧下降。图8为进距比在1.7、2.0、2.3时桨叶0.9倍展长处的压力系数Cp曲线。随着进距比的增大,翼型吸力面的负压区范围逐渐缩小,从前缘开始正压区范围逐渐扩大,而翼型的压力面则从前缘开始负压区逐渐扩大。图9为进距比1.7、2.0、2.3时0.9倍桨叶展长截面的压力云图。可见随着平飞速度的增大,驻点位置逐渐由下翼面转移到上翼面。当驻点位置在上翼面时,气流绕过前缘,速度逐渐增大,压强随之降低,因此进距比为2.0、2.3时,下翼面前缘附近形成负压区。由图9可见,平飞速度越大,驻点位置相对靠后,则气流绕过前缘需要经过更长的路程,气流速度更快,因此下翼面前缘区域压强更小。而在上翼面,由于驻点位置的影响,随着平飞速度增大,上翼面正压区逐渐增大,从而负压区缩小。桨叶驻点位置取决于桨叶前来流方向,桨叶前来流方向则由飞行速度和螺旋桨旋转速度构成的速度三角形决定。由于高空长航时无人机螺旋桨多为定桨距螺旋桨,结合图7、图8所呈现的趋势,根据速度三角形可知,螺旋桨转速不变,平飞速度增大,各个叶素的迎角变小甚至会变为负迎角,导致螺旋桨拉力和功率需求降低。当平飞速度超过某一值后,螺旋桨几乎不提供拉力,因此效率急剧下降。针对这一问题,一般采用调整螺旋桨转速的方法来解决。但是,由图8还可以看出,三个进距比工况下,桨尖均受到明显的压缩效应影响,这说明即便通过调整螺旋桨转速和飞行速度进行匹配以避免桨叶迎角的减小,但是桨尖压缩效应对螺旋桨气动性能的影响始终存在,因此,如何消除桨尖压缩效应是提高螺旋桨气动性能的关键。

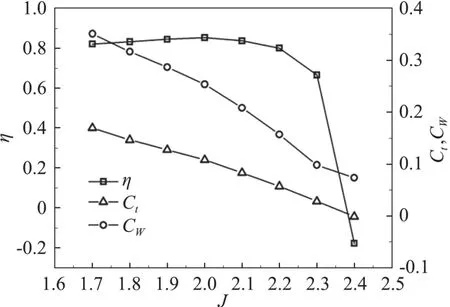
图7 无后掠桨叶性能曲线Fig.7 Performance curve of unswept-blade propeller

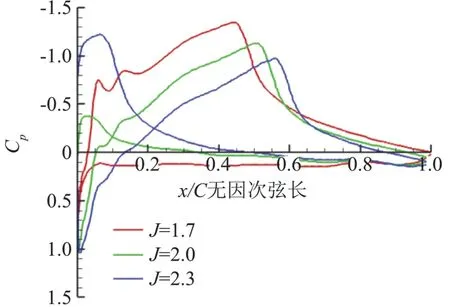
图8 随进距比增大压力系数曲线图变化对比Fig.8 Comparison of pressure coefficient curve with increasing of advance ratio

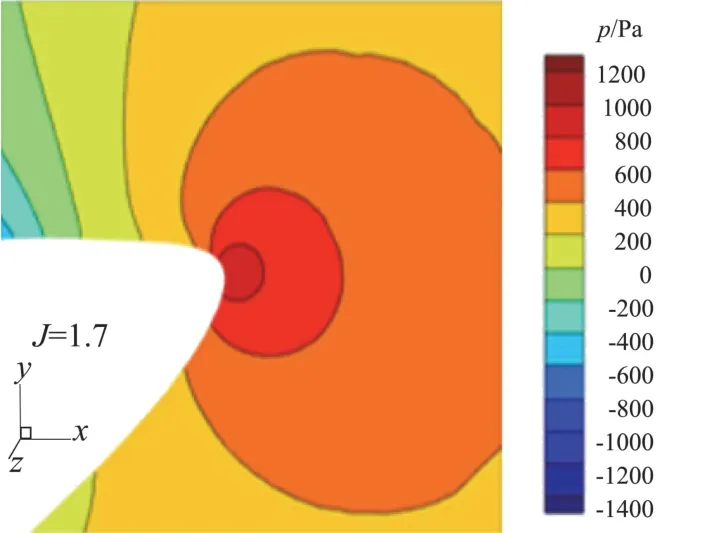
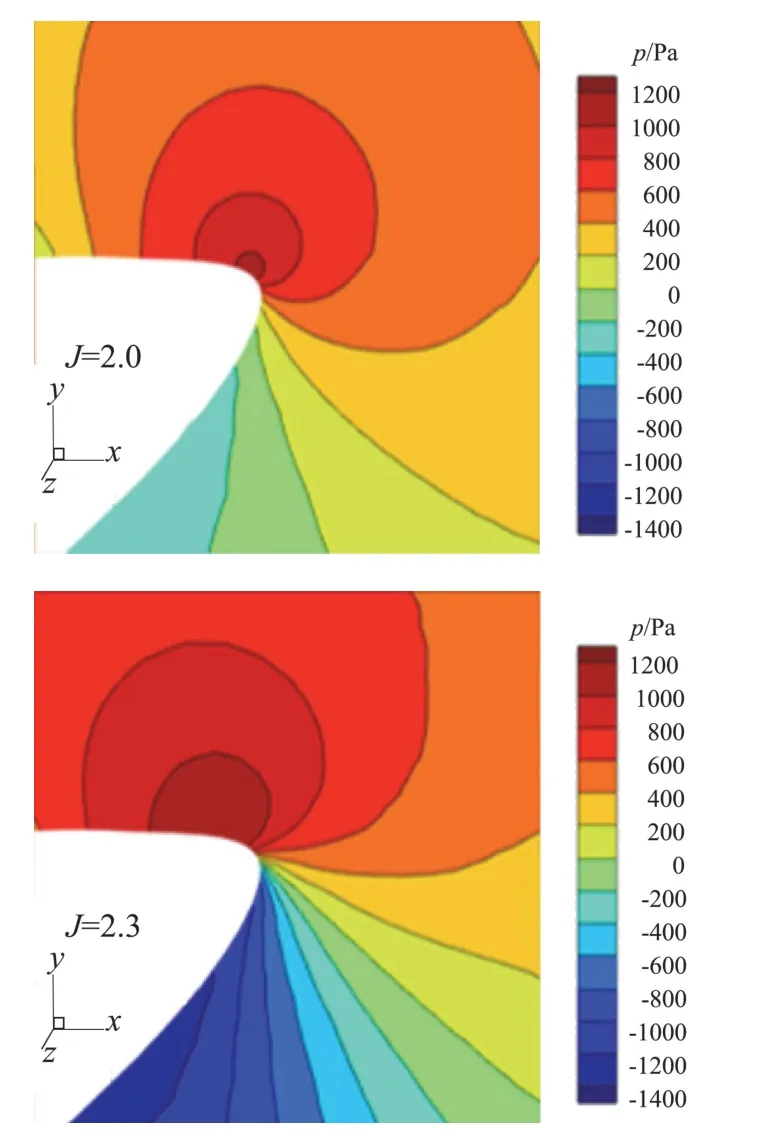
图9 不同进距比0.9倍展长压力云图Fig.9 Pressure distribution at 0.9 spanwise length location with different advance ratio

4 后掠桨叶计算结果及分析

根据第1.2节提到的不同后掠桨叶要保证桨尖切向速度相同的要求,可知不同后掠螺旋桨直径D和转速的乘积是一定值。又根据进距比的定义式:J＝v0/(Ns·D),可知不同后掠角的螺旋桨进距比和平飞速度一一对应,因此不同后掠角的螺旋桨气动性能可以放在同一段进距比的范围内进行比较。这样既可以表示各个螺旋桨自身的气动性能又可以进行不同后掠桨叶之间的性能对比。采用与无后掠桨叶相同的计算方法分别对各个后掠桨叶进行计算,结果分析如下。

图10~图12分别为不同后掠角螺旋桨的拉力、功率和效率对比图。由拉力对比曲线图可知,在平飞速度较低时(进距比1.7、1.8),随着桨叶后掠角的增大,拉力先增大然后降低,在此范围内桨叶后掠角为40°时拉力最大,进距比超过1.8之后,螺旋桨拉力随着桨叶后掠角的增大而增大,整体来看后掠桨叶螺旋桨都能提供比无后掠桨叶螺旋桨更大的拉力。由功率对比曲线可知,随着桨叶后掠角的增大,螺旋桨的功率需求也随之增大,且在较高平飞速度时对功率的需求更高。由效率对比曲线可知,桨叶后掠可以使螺旋桨在较高的平飞速度维持较为理想的效率,且后掠角越大,螺旋桨可在更高的平飞速度下高效工作。后掠角从10°增大到40°时,螺旋桨的峰值效率随着后掠角的增大而增大;当桨叶后掠角达到50°时,螺旋桨的峰值效率下降,且在较低的速度范围内,螺旋桨效率下降明显,不利于无人机低速巡航飞行。本文的计算结果还显示,当后掠角在30°时,螺旋桨在高速工作时的效率开始明显提高,最佳的后掠角应该在30°和50°之间,此时,螺旋桨在较低速度范围内效率变化不大,在较高速度范围内能够明显提高螺旋桨效率,有效加宽螺旋桨的工作范围。

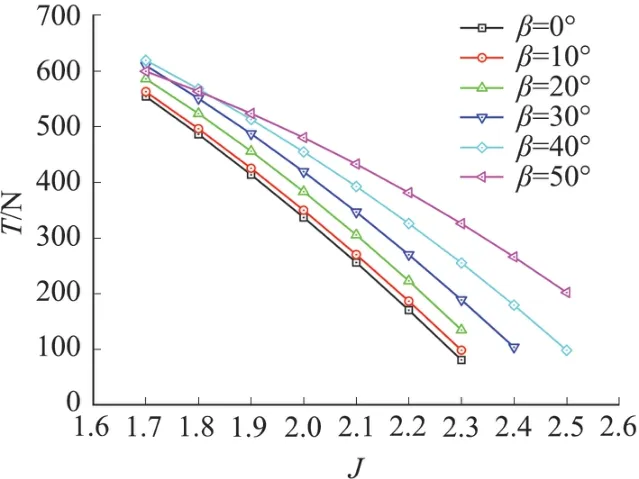
图10 不同后掠角螺旋桨拉力对比Fig.10 Thrust comparison for different sweep angles

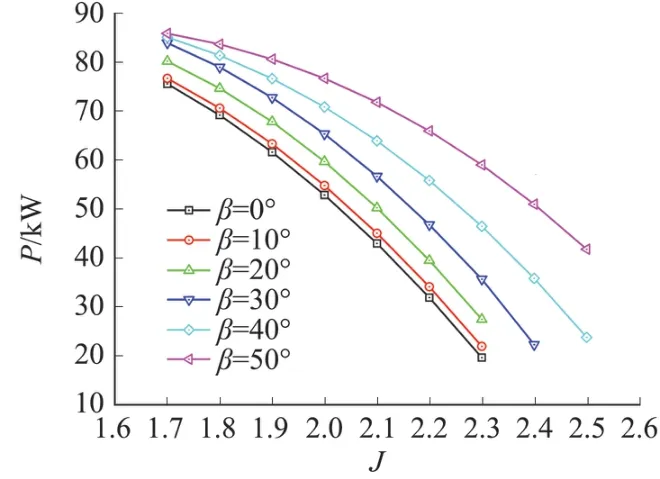
图11 不同后掠角螺旋桨功率对比Fig.11 Power comparison for different sweep angles

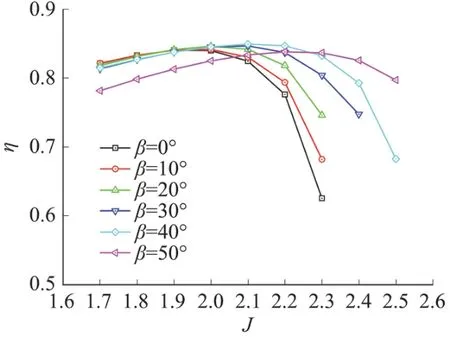
图12 不同后掠角螺旋桨效率对比Fig.12 Efficient comparison for different sweep angles

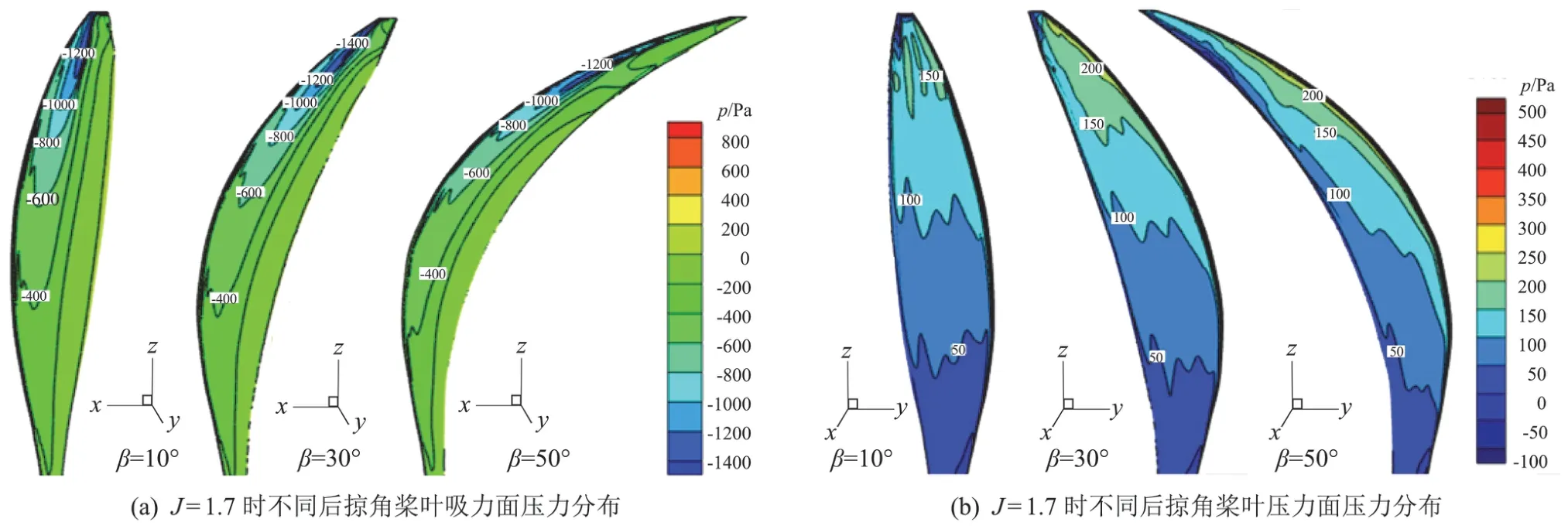
图13 J＝1.7时不同后掠角桨叶压力分布对比Fig.13 Comparison of pressure distribution on blade for different sweep angles at J＝1.7

现分析J＝1.7时,后掠角分别为10°、30°、50°桨叶吸力面和压力面的压力云图(图13),探究桨叶上压力分布随后掠角的变化规律。从图13(a)吸力面的压力值来看,随着后掠角的增大,负压值先增大后降低。从压力分布来看,当后掠角为10°、30°时,最大负压区都在桨尖处;当后掠角为50°时,最大负压区由桨尖向桨叶中部移动。从图13(b)压力面的压力云图来看,后掠角为10°、30°时,压力面的最大正压区在桨尖处,从桨尖到桨根压强逐渐减小;后掠角为50°时,压力面的最大正压区从桨尖下移到桨叶中上部。

图14为进距比1.7时、不同后掠角桨叶0.7倍展向截面的前缘压力云图。从图中可以看出后掠会导致驻点位置下移。图15为后掠桨叶叶素分布位置(红色方点)和无后掠桨叶叶素分布位置(蓝色点)对比,可以看出在各个展向位置,后掠桨叶的迎角都大于无后掠桨叶。正是因为后掠使得桨叶的平均迎角增大,后掠桨叶的功率需求更大,这一点也可以从图11功率对比图中得出。因为后掠会使得桨叶平均迎角变大,且随着后掠角增大,这种趋势更加明显,所以在图13(b)中后掠角为30°、50°时最大正压区域比后掠角为10°时大,而后掠角为50°时由于桨尖三维效应的缘故,在桨尖处的最大正压区域消失。同样由于迎角增大的原因,在图13(a)中,后掠角30°时的最大负压高于后掠角10°时的最大负压,但是后掠角为50°时由于三维效应的缘故最大负压值又低于后掠角为30°的桨叶,因此在三维效应和迎角增大的共同影响下,使得三种桨叶中,后掠30°的桨叶能提供最大的拉力。

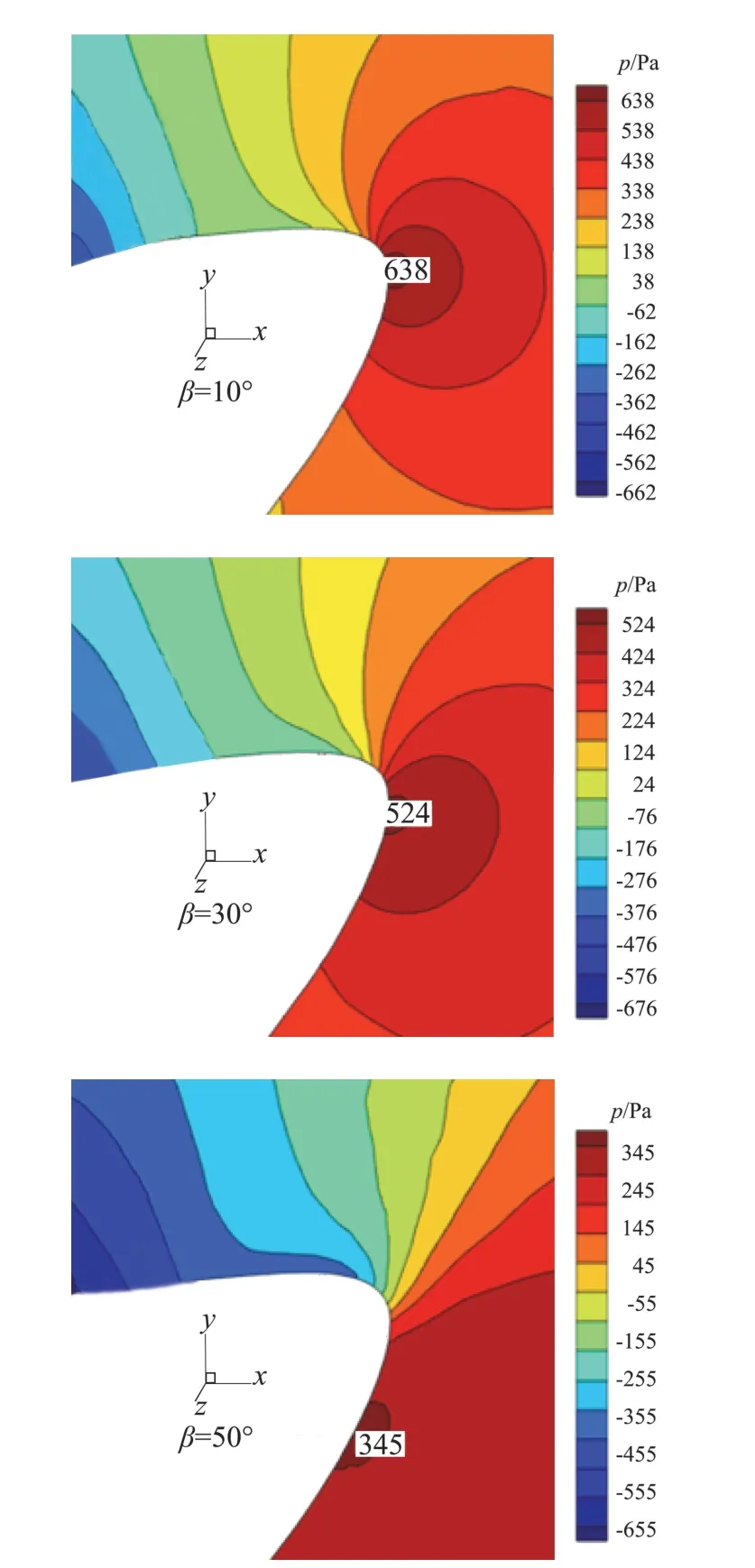
图14 不同后掠角前缘驻点c位置对比Fig.14 Comparison of leading edge stagnation point location for different sweep angles

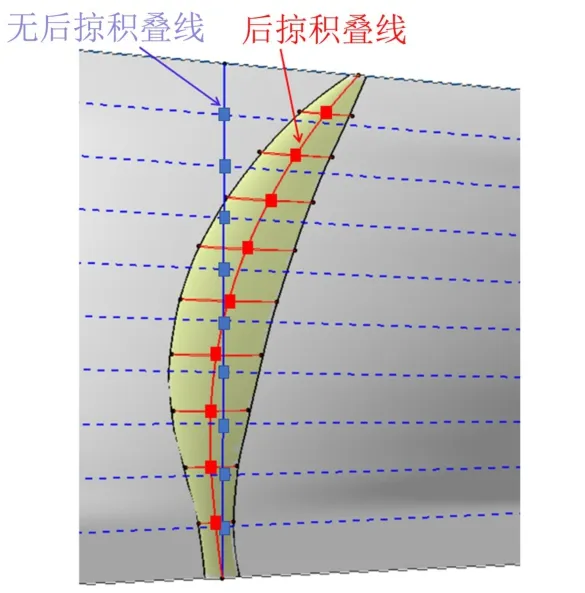
图15 后掠和无后掠桨叶叶素分布位置对比Fig.15 Comparison of blade elements position of swept and unswept blade

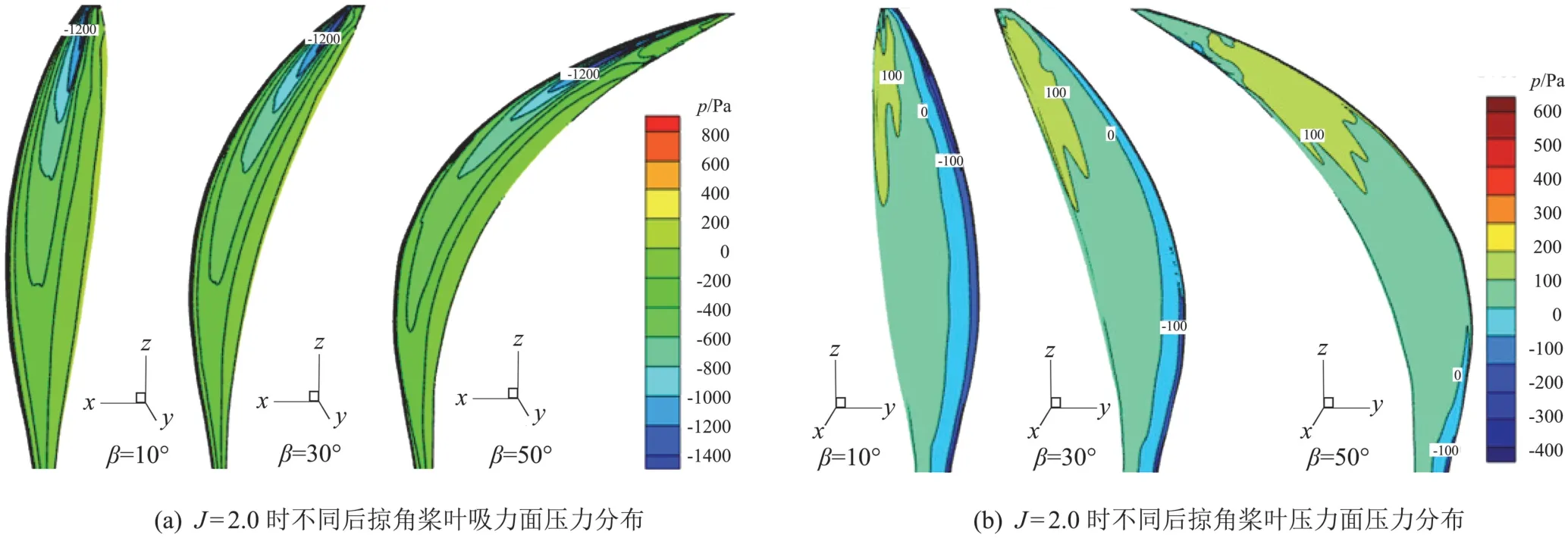
图16 J＝2.0时不同后掠角桨叶压力分布对比Fig.16 Comparison of pressure distribution on blade for different sweep angles at J＝2.0

图16为进距比2.0时,后掠角分别为10°、30°、50°时桨叶吸力面和压力面的压力云图。吸力面的压力变化情况和进距比为1.7时有相同之处也有所区别:后掠角为10°、30°时最大负压区在桨尖处,后掠角为50°时同样由于桨尖三维效应的缘故,使得最大负压区向桨叶中部移动。压力面和吸力面的压力值变化情况与进距比为1.7时有所不同,由图9可知进距比为2.0时,桨叶处在负迎角的工作状态,因此在压力面能够看到明显的负压区域,因为后掠使得桨叶的迎角变大,从而在进距比2.0时,后掠50°的桨叶迎角大于后掠10°、30°的桨叶,即后掠50°的桨叶更接近于正迎角的工作状态,气流从上翼面绕过前缘到达下翼面的过程中,压降不及后掠角为10°、30°时剧烈,因此在图16(b)中可以看到,后掠角为50°时,在压力面前缘附近形成的负压区域小于另外两种情况,从吸力面压力分布可见,三个桨叶的最大负压值相同,这是由于迎角为负及迎角随后掠角的变化导致,后掠50°时更接近正迎角,因此气流在前缘处可以更加充分的加速,使得其最大负压值能够相等于其余两个后掠桨叶。这正是图10中当进距比在1.9之后,后掠角为50°的桨叶所产生的拉力最大的原因。

图17为进距比1.7时,后掠角分别为0°、30°时0.95倍展长处切面的压力云图,由图可见在桨尖处有明显的压缩效应,后掠角0°时,桨尖处形成了激波,激波后与激波前绝对静压比为1.45,当后掠角为30°时,激波减弱,波后、波前绝对静压比为1.41,可见桨叶后掠可以减弱桨尖激波强度,这也是后掠桨叶比无后掠桨叶能够提供更大拉力的原因。由于本文所用螺旋桨工作高度较高,大气密度低导致雷诺数较低,附面层较厚,气流在上翼面易发生分离,由图可见在上翼面存在激波-附面层干扰现象,并且后掠角越大激波-附面层干扰现象越明显,这是因为后掠会使得桨尖附面层变厚,本文认为激波-附面层干扰一定程度上减弱了桨叶上表面的激波强度,这可以从图17压力云图及图18压力系数曲线对比图中看出。由压力系数曲线对比(图18)可见,由于后掠角30°时的当地迎角大于后掠角0°时的当地迎角,因此在激波前,后掠角30°时吸力更大,在激波之后,一方面由于后掠减弱了激波强度,另一方面由于激波-附面层干扰的作用使得后掠角30°时的吸力更大。

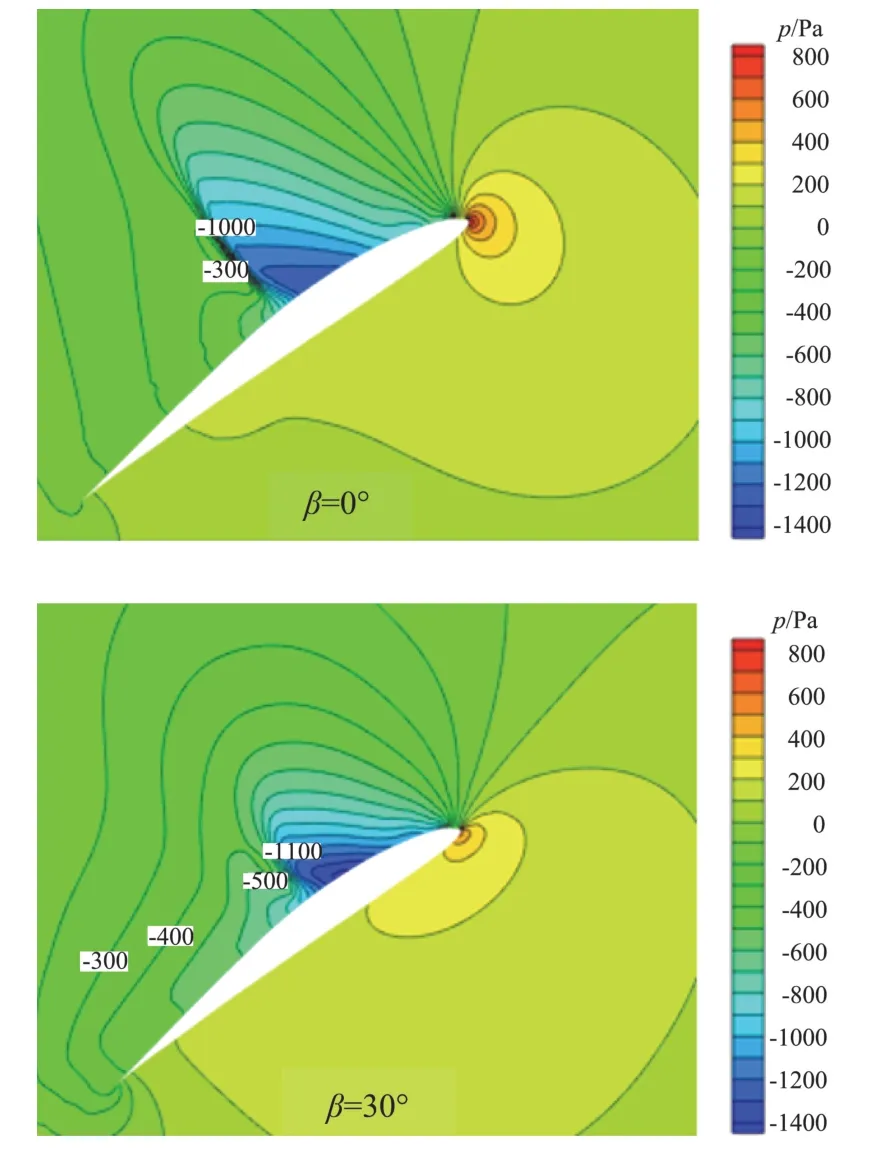
图17 J＝1.7时后掠与不后掠桨叶桨尖激波比较Fig.17 Comparison ofshock wave at blade tip between swept and unswept blade

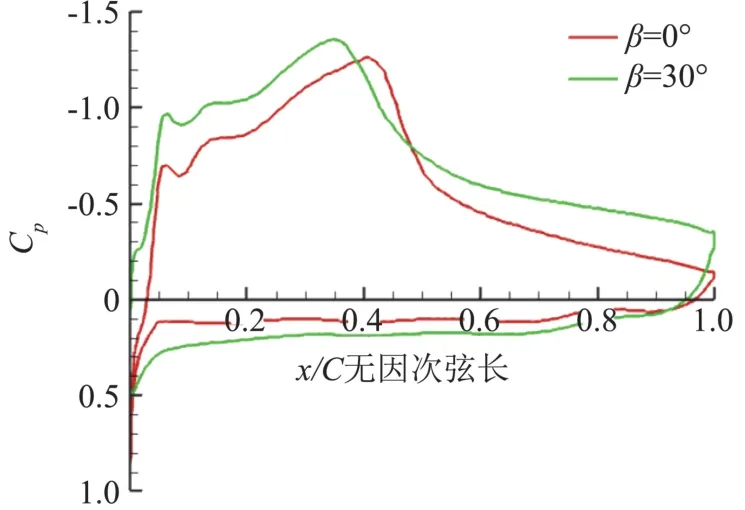
图18 J＝1.7时后掠与不后掠桨叶桨尖压力系数比较Fig.18 Comparison of pressure coefficient at blade tip between sweptand unswept blade

5 结 论

本文将桨叶后掠的设计思想应用于高空长航时无人机螺旋桨桨叶设计上,在无后掠桨叶的基础上,分别设计了五个后掠桨叶,应用数值计算方法,分析了高空长航时无人机螺旋桨在高速工况时效率下降的原因,对比了不同后掠角螺旋桨拉力、功率和效率的变化趋势,分析了后掠对桨叶气动性能影响的原因,得出如下结论:

提高螺旋桨高速性能的关键在于减弱桨尖压缩效应,后掠桨叶能够达到这一目的,但是后掠桨叶的气动性能受迎角变化、桨尖三维效应、桨尖激波强度、激波-附面层干扰综合影响。当桨叶后掠角在30°和50°之间时,可使螺旋桨能够在原设计点之后加宽螺旋桨的高效工作范围,提高高空长航时无人机的高速性能,满足无人机快速爬升和快速机动的设计要求。