基于熵产理论设计方法的多目标翼型优化

王 威,王 军,梁 钟,李佳峻

(华中科技大学 能源与动力工程学院,武汉 430074)

0 引 言

翼型广泛应用于航空航天、风力发电等诸多流体机械领域,其性能对流体机械的工作性能起着至关重要的影响。高性能叶片和飞行器的设计中已不直接采用现有的翼型,而是对翼型进行优化设计,寻找到功能符合设计要求的高性能翼型。传统的翼型优化[1-4]在研究其升阻力系数、效率等空气动力学性能、结构特性等单一学科要求的基础上,来进行翼型的改进、修型,但这些参数不能反映流场内局部损失的具体来源和增加过程。如果能够掌握流场中能量损失的大小及分布,可以针对局部损失较大的区域进行优化设计,通过降低局部损失来改善压气机性能。

熵产理论基于热力学第二定律,在不可逆现象比较集中的传热与流动系统得到了广泛深入的研究。由于熵产的大小揭示了过程的不可逆程度,反映了过程中能量转换与利用的完善程度,国内外学者创造性地将其用于翼型、风机叶片以及飞行器的设计中。Shehata等[5]将熵产最小原理用于叶片性能分析中,分析了不同迎角下、不同翼型截面的热力学第二效率。Mortazavi等[6]将熵分析方法和神经网络算法引入轴流风机叶片翼型截面优化中,分析了低雷诺数下NREL系列翼型截面的火用效率。Li和Figliola[7]将熵产作为优化目标对二维翼型进行多目标气动优化设计,并分析了熵产与翼型阻力的关系。王松龄等[8]基于熵产理论对离心风机叶轮进行参数化优化设计,优化后叶轮和蜗壳熵产明显降低,流动得到改善。

本文将熵产方法引入到翼型优化设计中,研究流场熵产在翼型气动优化设计中的作用。通过建立参数化、网格生成、CFD计算、数值优化方法一体化的翼型优化平台,完成特定工况下以最大升阻比和最小熵产率为优化目标的多目标翼型优化设计。

1 熵分析优化模型建立及求解

1.1 系统熵方程及熵产计算

熵产代表了流动中能量损失的大小和系统的不可逆程度,根据热力学第二定律,单位体积流体的熵产率[9-10]为:

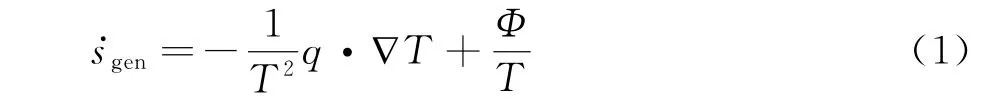
其中Φ为耗散函数,其张量形式表达式为:

式(1)表明引起流场熵产的因素是黏性引起的耗散和有限温差引起的传热,其中耗散引起的熵产取决于流体的黏性和速度场,传热引起的熵产取决于流体的导热率和温度场。

当低速不可压且不考虑传热时,由传热项引起的流场熵产可忽略不计。因此,对于二维不可压流场中单位体积熵产率可进一步简化为:

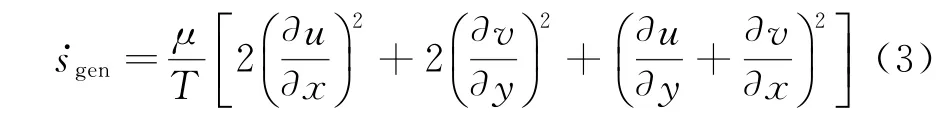
当流动为湍流时,本文采取雷诺平均法(RANS)对上式进行时均运算,由于T′作为分母出现在高阶项,故可忽略,可得:

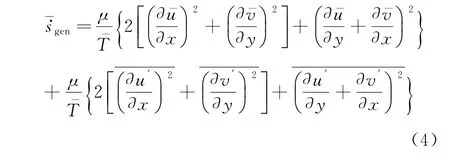
式(4)表明,湍动流动过程中的耗散所引起的熵产可以分成两项,第一项是由于黏性耗散引起的,第二项是由于速度脉动所引起的湍流耗散产生。

根据Boussinesq的涡黏性假设,有

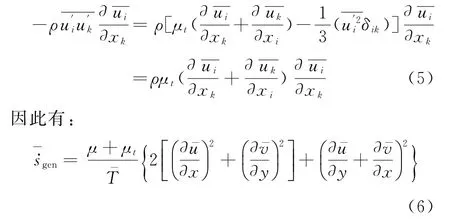
式中μt为湍流动力黏性系数,它是空间坐标函数,取决于流动状态而不是物性参数。

对式(6)进行体积分,即可得到流场熵产率:

1.2 翼型参数化方法

本文采用Kulfan和Bussoletti[11-12]提出的CST(Class Shape Transformation)参数化方法,对于钝前缘、尖尾缘翼型,翼型几何型面的具体参数表达式如下:

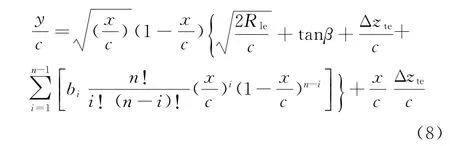
式中,c为翼型弦长,x、y为翼型横、纵坐标,Δzte/c为翼型后缘点纵坐标,Rle为翼型前缘半径,β为后缘处的切线倾角,bi(i＝1,2,…,n－1)为引进的权重因子。

为限制翼型上下表面曲线在后缘处封闭,故上下表面曲线的Δzte/c相等。因此,翼型的设计参数为翼型前缘半径Rle,后缘点纵坐标Δzte/c,上表面曲线在后缘处的切线倾角β和翼型后缘角βte,上、下表面控制参数,(i＝1,2,…,n－1)。

本文分别采用7阶Bernstein多项式对NACA0012和RAE2822进行参数化拟合,并与翼型数据库中翼型数据进行对比,拟合效果如图1所示,由图可知,拟合出的翼型如与初始翼型符合得较好,充分体现了CST参数化方法的优点。

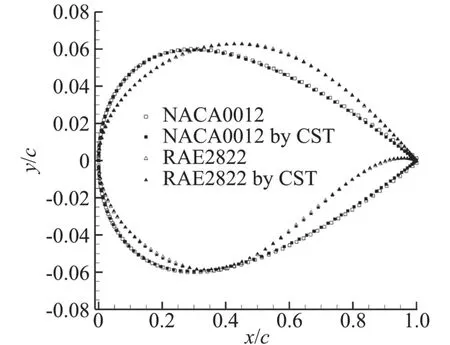
图1 NACA0012和RAE2822翼型CST参数化效果图Fig.1 CST parametric representation of NACA0012 and RAE2822

1.3 流场数值计算

翼型的计算域和计算网格如图2所示,翼型弦长为c;入口边界距机翼前缘11.5c,为半径12.5c的半圆;出口边界距机翼后缘,采用C型结构网格,用四套网格:200×70、200×80、200×90和200×100进行网格无关性验证,本文采用200×80网格进行计算。

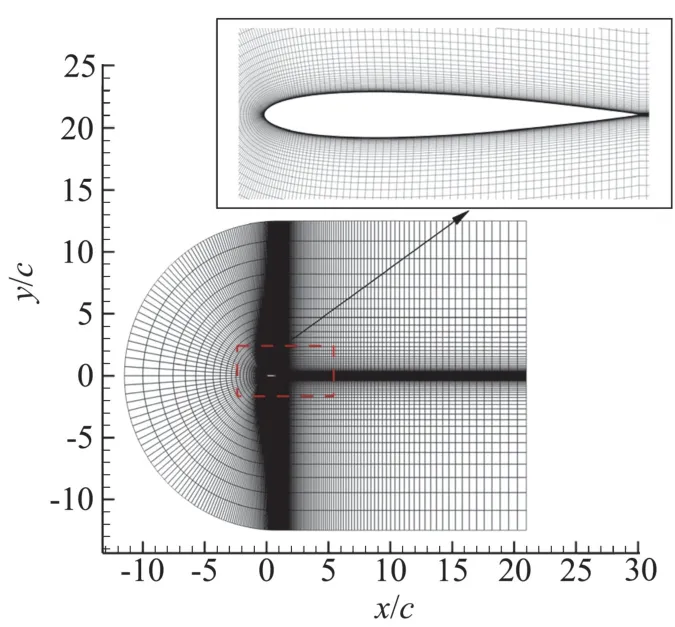
图2 NACA0012翼型流场计算网格图Fig.2 Computational mesh of NACA0012 flow field

对翼型进行优化前,需要对数值计算结果进行验证,将其与实验数据进行对比,从而对计算的可信度和优化质量提供客观的评价标准。本文计算工况为来流雷诺数2.88×106,进出口温度为299.15 K,计算迎角分别为0°、5°、10°和15°。湍流模型采用S-A单方程模型,边界条件设置为速度入口、压力出口,采用二阶迎风格式离散控制方程,选择压力基求解器,速度和压力耦合采用SIMPLE算法,残差控制在1×10－4数量级。

图3为NACA0012翼型在迎角0°、10°和15°下的压力系数分布与文献[13]中实验数据的对比。其中实验来流速度为55 m/s,模型弦长为0.76 m,雷诺数为2.88×106。表1为迎角0°、5°和10°下数值计算NACA0012翼型升、阻力系数和文献[14]实验数据对比,可以看出:数值计算得到的压力分布与风洞实验数据非常接近,升力系数的数值计算结果与实验值相当,阻力计算存在一定误差,数值结果表明此时流场网格划分和数值计算的设置适用于该工况下翼型流场计算。

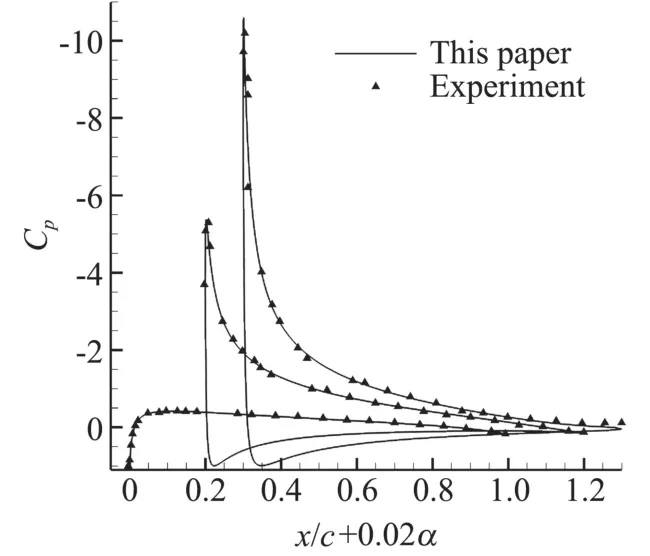
图3 0°、10°和15°迎角下压力系数分布与实验值比较Fig.3 Comparison of the pressure coefficient distribution obtained from calculation and experiment

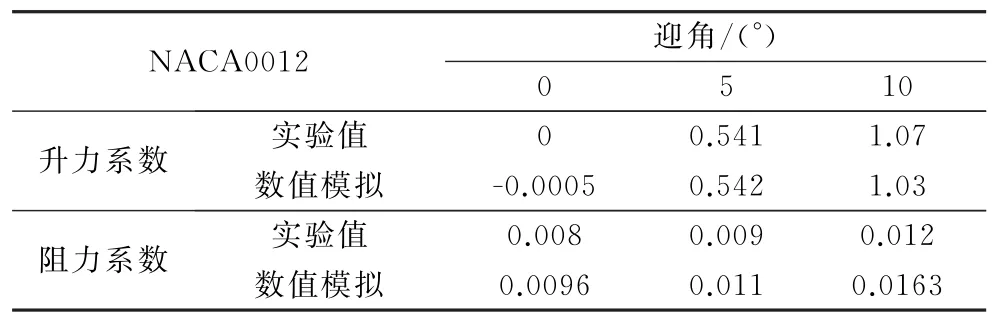
表1 不同迎角下升、阻力系数与实验值对比Table 1 Comparison of the lift and drag coefficients obtained from calculation and experiment

1.4 优化模型及流程

优化的数学表达式为:

其中,D为优化设计空间,d为优化设计变量的向量,gi(X)为约束条件。

将优化算法、CST参数化建模、翼型网格生成、流场CFD计算进行耦合,生成适用于多目标翼型优化的计算程序。根据CST翼型参数化方法,输入设计变量的值,生成翼型坐标点数据文件,继而完成翼型网格生成。通过翼型流场CFD计算,输出翼型气动性能数据文件。

在翼型的优化设计中,设计变量与目标函数之间存在复杂的非线性关系,本文采用遗传算法进行优化计算。对于多目标优化问题,采用带精英策略的非支配排序遗传算法(NSGA2)[15]。它应用Pareto最优解理论来处理多目标优化问题,由于各个目标没有人为地设定权重分配,所以所有Pareto最优解的集合构成了该问题的Pareto最优解集。此外NSGA2算法采用快速非支配排序方法和精英策略,降低了算法的计算复杂度,提高了计算效率。NSGA2优化算法将翼型气动性能数据作为输入文件,根据遗传算法既定的输入参数,计算各个翼型的适应度来决定下一代种群的个体(翼型),从而形成一个优化循环。

2 优化结果与分析

根据上述优化流程,本文对NACA0012翼型进行单目标和多目标优化设计。算例一为基于熵产的多目标优化设计方法,优化目标为升阻比最大以及熵产最小,约束条件为升力系数以及设计变量的几何约束。算例二为传统的翼型气动优化设计方法,优化目标为阻力系数最小,约束条件与算例一一致。其数学描述分别为:

翼型的设计状态为来流雷诺数为2.88×106,飞行迎角5°,流场网格和CFD参数设置选择上述经验证的设置。翼型的参数化方法选择CST方法,设计参数和相应的约束范围如表2所示。

表2 设计变量名称、取值范围Table2 Range of design variables

优化设计的各优化控制参数选取为:初始种群规模为80,进化代数为50,杂交概率为0.70,变异概率为0.12,变量采用实数编码。

两种算例优化过程中的种群分布如图4、图5所示。可知,初始种群分布混乱,会出现升阻比小的个体,经过数代进化后,通过杂交、变异,淘汰了部分劣势个体,种群的分布朝好的方向进化,但仍呈现不规律性。第10代以后有收敛的趋势,在以后的优化中,收敛趋势更加明显,不断优化出升阻比更大、熵产率或阻力系数更小的个体,说明优化的全局收敛性。

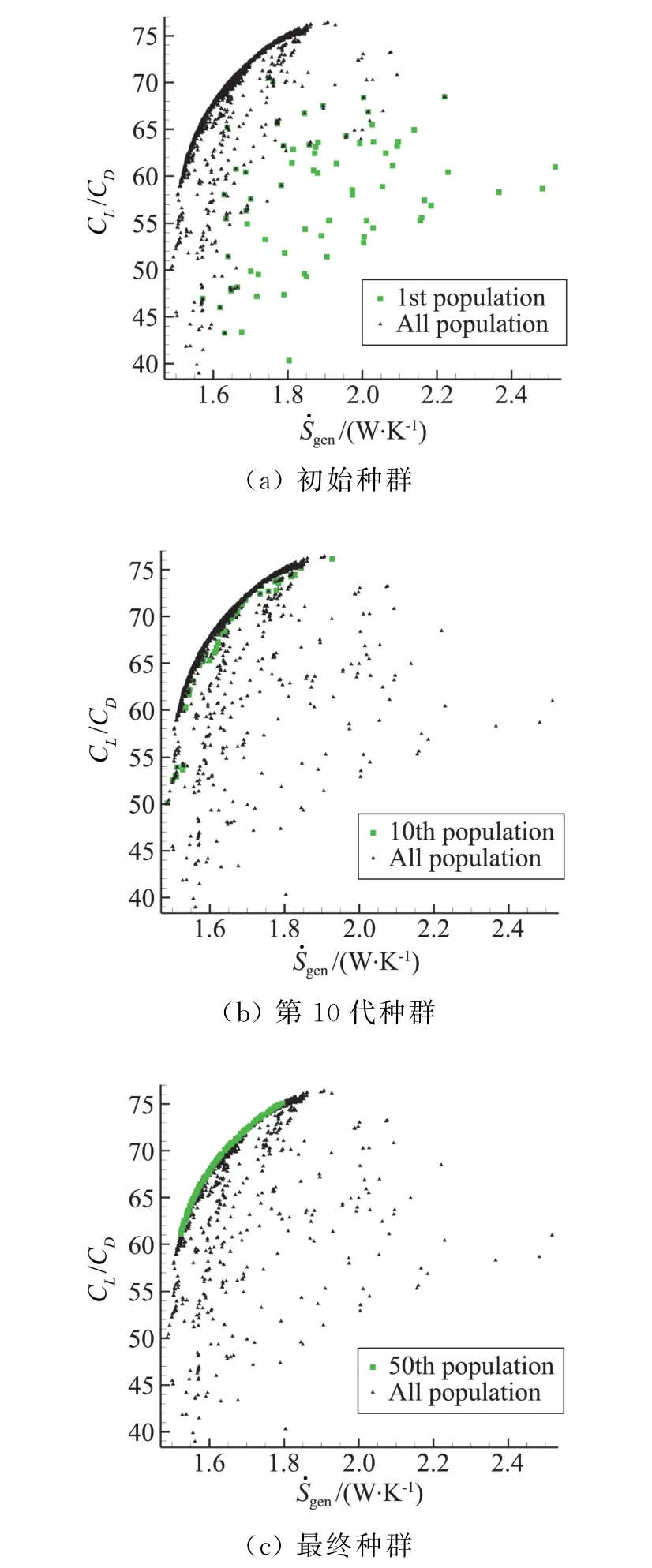
图4 算例一优化过程种群分布情况Fig.4 Population distribution in optimization procedure in case 1

图6(a、b)为两种算例下优化后翼型目标函数的Pareto分布,可以看出采用基于熵产率作为优化目标的算例一得到的优化翼型具有相对较大的升阻比。图中Pareto分布中每个数据点代表一种可行的优化翼型,它是两种互为矛盾的优化目标不断调和的结果,因此可以根据设计需要选择合适的最优翼型。由Pareto分布图我们可以看出,翼型的升阻比越大,对应流场的熵产率越大,变化趋势与文献[7]一致。因此提高翼型的升阻比,是以较大的流动损失作为代价的。

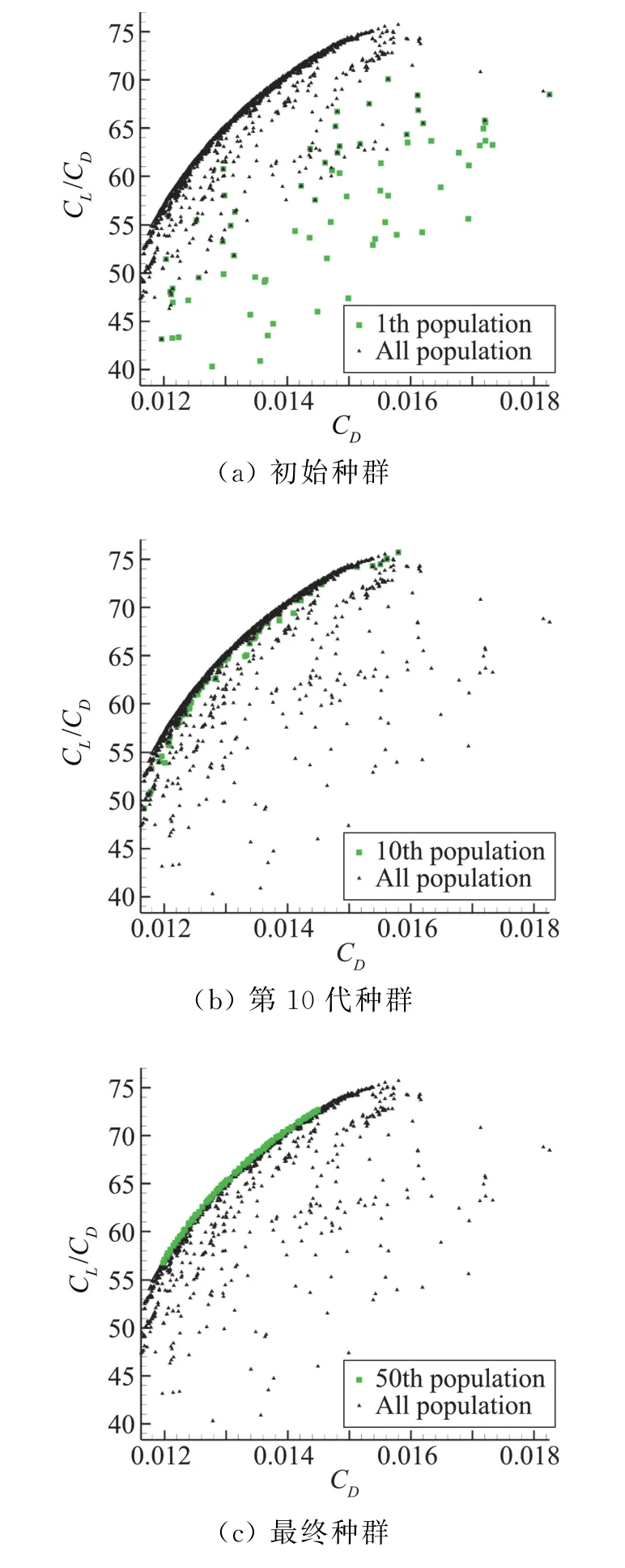
图5 算例二优化过程种群分布情况Fig.5 Population distribution in optimization procedure in case 2

同时,图6也给出了四种优化翼型的压力云图和熵产率云图,四种优化翼型分别为两种算例中Pareto分布中对应的最大、最小升阻比对应翼型(分别命名为Opt_1、Opt_2、Opt_3和Opt_4,如图所示)。由压力云图可知四种翼型升阻比越大,翼型下表面高压区越大;由熵产率云图可知翼型的流动损失主要发生在翼型前缘、近壁面以及尾缘处,熵产云图可以准确反映出翼型流动损失较大的部位,四种翼型熵产率越小,翼型尾缘处的流动损失越小,而前缘和壁面处的损失几乎不变。

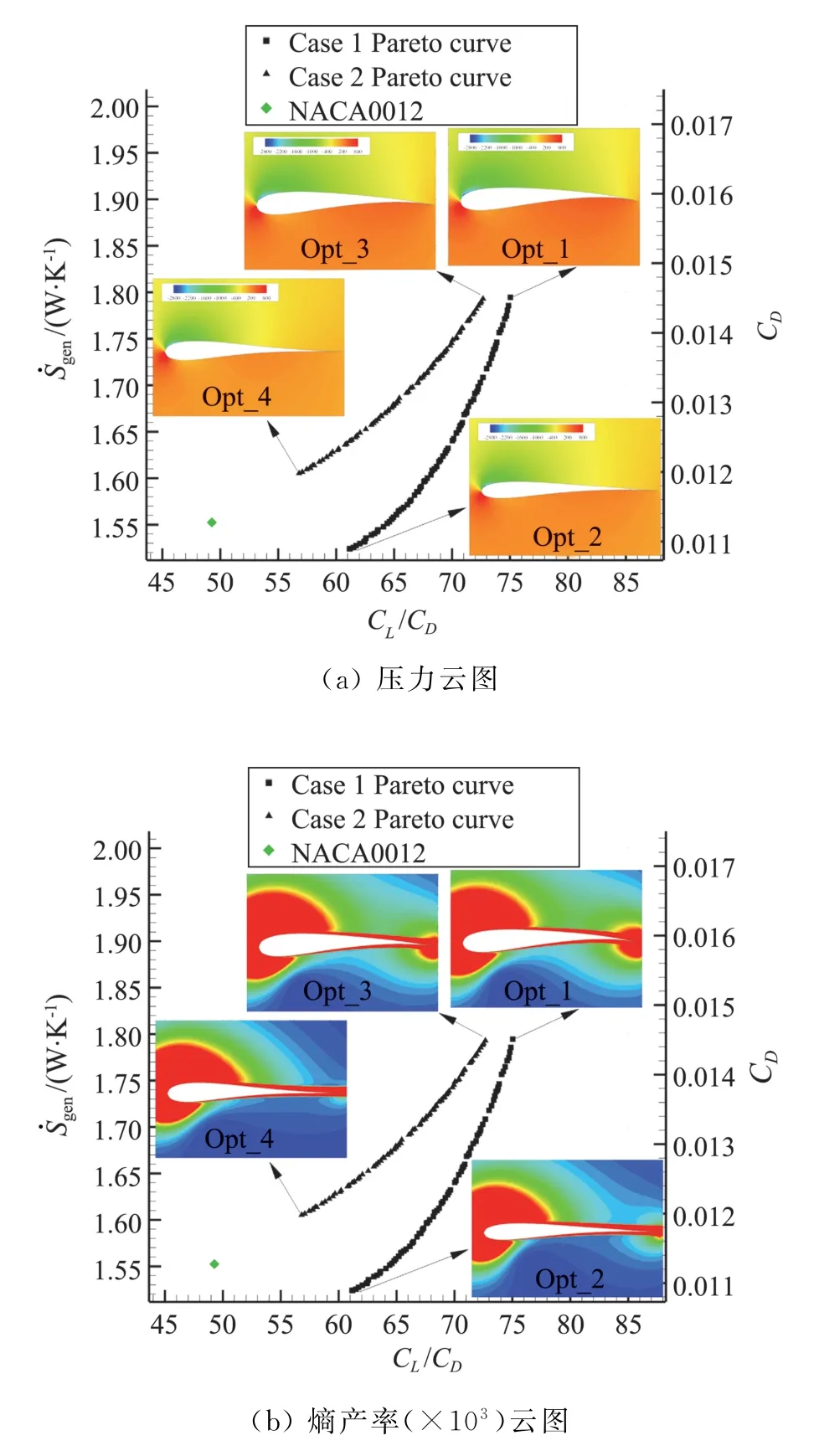
图6 优化翼型目标函数的Pareto分布Fig.6 Pareto curve of the airfoil shapes optimization

表3给出了对应四种优化翼型的气动性能对比,可知翼型优化后升力系数得到很大程度提高,阻力系数亦有所增加。但升阻比相比于基准翼型仍有很大提高。本文优化结果与文献[16]对RAE2822翼型进行气动外形优化设计后气动性能提高具有相似之处。基于熵产理论的优化翼型相比于传统的基于最大升阻比和最小阻力系数的优化翼型,能够在控制流动损失的前提下,得到升阻比尽可能大的翼型。优化翼型Opt_1和Opt_2为基于熵产理论优化得出,可以看出相比于基准翼型,其升阻比分别提高了52.28%和24.13%。

图7(a、b)分别为上述两组优化算例的四种优化翼型压力系数分布和几何外形与初始翼型的对比。图7(a)为两组算例Pareto解中最大升阻比对应的翼型Opt_1和Opt_3。可以看出,优化后的翼型弯度增加明显,前缘半径亦有所增加,该变化情况与对应的升力系数增加明显、阻力系数增大结果与文献[17]具有一致性,翼型升阻比得到提高。翼型上表面厚度增加,有利于增加上表面流动速度,从而降低上表面压力,弯度增大,翼型下表面向内凹进,便于产生更大升力。由压力系数分布亦可以看出,上、下表面压力系数明显降低,使得升力系数明显提高。虽然前缘半径增大使得阻力系数增大,但升力系数增幅大于阻力系数增幅,使得升阻比相对于基准翼型仍有所增大;图7(b)为两组算例Pareto解中最小升阻比对应的翼型Opt_2和Opt_4,两组翼型的厚度明显变小,翼型下表面内凹,使得下表面压力系数变大。相比于NACA0012,两组优化翼型的前缘半径减少。

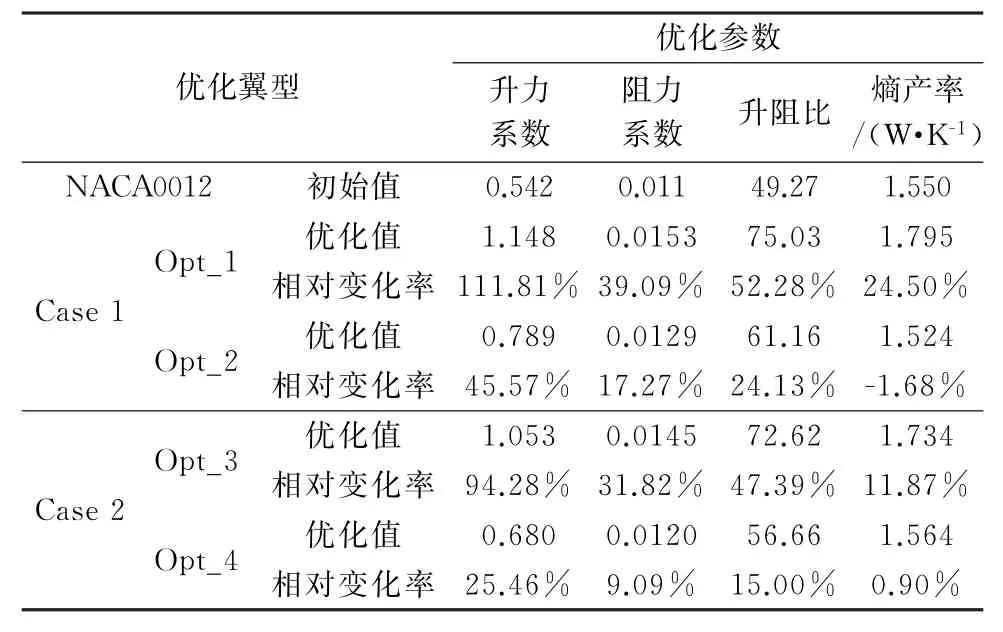
表3 优化翼型气动性能对比表Table 3 Comparison of aerodynamic characteristics of optimized airfoil

3 结 论

本文基于熵产理论对翼型的优化设计进行了一些探索,并与传统的翼型优化设计方法进行了对比。其研究目的并不是要取代传统的翼型优化设计方法,而是基于热力学第二定律提出一种新方法,作为传统方法的一种补充。

通过参数化方法完成翼型参数化建模,并采用遗传算法,最终对来流雷诺数为2.88×106,飞行迎角5°的翼型进行多目标优化,得出如下结论:

(1)将优化算法、CFD求解器、参数化方法和网格变形方法进行了耦合,实现了二维翼型的多目标优化设计,NSGA2优化算法在小种群优化中表现出良好的收敛性,能够满足复杂的非线性优化设计要求。

(2)CST翼型参数化方法有效减少了翼型设计变量的个数,提高了优化设计的效率,为未来三维复杂气动外形优化设计提供了良好的参数化设计基础。(3)相比于传统的翼型气动优化设计方法,基于熵产理论的气动优化设计方法能够具体掌握能量损失的大小及分布,得到气动性能更佳的翼型。

(4)通过对NACA0012翼型的多目标优化设计结果表明:与初始种群相比,最终优化翼型在升阻比提高的条件下,流场熵产率减少,能量效率提高。