基于贝叶斯统计推断的时间序列预测模型的优化

王 安

(桐城师范高等专科学校 商贸与电子信息系,安徽 桐城 231400)

贝叶斯时间序列建模与分析是统计学中一个重要的理论与实践课题。早期的学术研究开始了贝叶斯时间序列建模[1-2]。在欧美国家,贝叶斯模型首先取得了良好的效果,对于预测分析的效果改善明显,而使得其得到了广泛的使用。相较于非贝叶斯模型,贝叶斯模型更加灵活,正因为这个特点,更多的学者、专家以及相关行业的从业者,逐渐对贝叶斯模型持认可的态度[3-4]。尤其是近些年来,贝叶斯方法在社会经济预测分析中的应用逐年增加,并取得了很大的成功。贝叶斯统计推理可以应用的范围十分广泛,上至核电厂的工程质量控制、国家经济民生相关的数据统计分析,下至对社会犯罪情况的分析与预测,包罗万象。贝叶斯方法完全可以说是人们生产生活中的一个有力的工具[5]。但就目前的研究状况来说，贝叶斯方法在我国的应用和发展还处于起步阶段:一是与西方国家相比,我国目前的观点受到频率学派的限制,大多数统计专著和学术论文缺乏严格、系统的讨论，使国内学者对贝叶斯方法感到陌生[6-7]。二是由于缺乏相应的软件支持,高维数据分析中的复杂问题难以计算。该问题的求解阻碍了贝叶斯方法在实际问题中的应用。

1 ARMA模型

1.1 模型

作为最常用的拟合平稳时间序列的模型,ARMA模型共有三类,分别为AR模型、MA模型和ARMA模型。ARMA模型本身是一种自回归的移动平均模型,具有自回归模型和移动平均模型二者的特性。

AR(p)模型——p阶自回归模型

xt=φ0+φ1xt-1+…φpxt-p+εt

由于该序列是平稳序列,据此可推导得出均值为如下形式:

若φ0=0,则该模型称为中心化的AR(p)模型;若想对非中心化的平稳时间序列,进行中心化操作,则可做如下的变换:

Φp(B)=I-φ1B-…-φpBp称为p阶自回归多项式,则AR(p)模型可表示为:Φp(B)xt=εt,其中为延迟算子。

1.2 格林函数

格林函数反映了影响效应衰减的快慢程度(回到平衡位置的速度)是用来描述系统记忆扰动程度的函数,Gj表示扰动εt-j对系统现在行为影响的权数。

1.3 模型的方差

1.4 模型的自协方差

对中心化的平稳模型,可推得自协方差函数的递推公式:

γ(K)=φ1γ(k-1)+φ2γ(k-2)+…+φpγ(k-p)

用格林函数显示表示:

对于AR(1)模型,

1.5 模型的自相关函数

递推公式:

ρ(k)=φ1ρ(k-1)+φ2ρ(k-2)+…+φpρ(k-p)

如图1所示,平稳AR(p)模型的自相关函数有两个显著的性质[8]:

1)拖尾性。自相关函数总是有一个非零值,当k大于某个常数时,ρ(k)不等于零。

2)负指数衰减。随着时间的推移,自相关函数ρ(k)会迅速衰减,且以负指数(其中λi为自相关函数差分方程的特征根)的速度在减小。

(a)自相关函数ACF(k)xt=0.8xt-1+εtFig(a) Autocorrelation function of ACF(k)xt=0.8xt-1+εt

(b)自相关函数ACF(k)xt=-0.8xt-1+εtFig(b) Autocorrelation function of ACF(k)xt=-0.8xt-1+εt

图1AR(1)模型的自相关函数
Fig.1AutocorrelationfunctionofAR(1)model

1.6 模型的偏自相关函数

如图2(a-b)所示,自相关函数ρ(k)实际上并不只是xt与xt-k之间的相关关系,它还会受到中间k-1个随机变量xt-1, …,xt-k+1的影响[9]。为了消除随机变量在中间造成的干扰,我们将单纯测量xt与xt-k之间的相关关系,引入了滞后k偏自相关函数(PACF),计算公式为:

其中,

实际上k阶自回归模型第k个回归系数φkk就是滞后k偏自相关函数:

xt=Φk1xt-1+Φk2xt-2+…+Φkkxt-k+εt

两边同乘以xt-k,求期望再除以γ(0)得到:

ρt=Φk1ρt-1+Φk2ρt-2+…+Φkkρt-k,t=1,2,…,k,…,n

取前K个方程构成的方程组:

…

ρ1=Φk1ρk-1+Φk2ρk-2+…+Φkkρ0

称为Yule-Walker方程,可以解出Φkk。

(a)偏自相关函数PACF(k)xt=0.8xt-1+εt(a) Partial autocorrelation function of PACF(k)xt=0.8xt-1+εt

(b)偏自相关函数PACF(k)xt=-0.8xt-1+εt(b) Partial autocorrelation function of PACF(k)xt=-0.8xt-1+εt

图2AR(1)模型的偏自相关函数
Fig.2PartialautocorrelationfunctionofAR(1)model

2 ARIMA模型——混合自回归移动平均模型

ARIMA 是一种单变量同方差的线性模型,对于满足参数模型的平稳时间序列,主要有以下三种基本形式:自回归模型(AR:Auto-Regression),移动平均模型 (MA:Moving-Average)和混合模型 (ARIMA:Auto-Regression-Moving-Average)[9]。

简短地说, AR模型是建立当前值和历史值之间的联系,MA模型是计算AR部分的误差的累计,此模型是分析两者与差分的和。

2.1 原理

它用于处理单变量同方差的非平稳时间序列,并通过差分法或适当的变换转化为平稳时间序列,再使用ARMA模型,这种模型也称Box-Jenkins模型。

残差的条件方差是异方差的时间序列,适合用GARCH模型。ARIMA(p,d,q)模型的形式如下:

其中,Δd=(I-B)d为d阶差分,

Φ(B)=1-Φ1B-Φ2B2-…-ΦpBp

Θ(B)=1-θ1B-θ2B2-…-θpBp

d阶差分后的序列可表示为:

2.2 建模流程

2.2.1识别阶段

在识别后面ARIMA模型之前,首先需要指定响应变量序列,计算自相关系数(ACF)、逆自相关系数(IACF)、偏自相关系数(PACF)和相关数。在这个工作阶段,通常有几个ARIMA模型可供选择,要区分模型的类型需要通过检验样本自相关系数(SACF)和样本偏自相关系数(SPACF)。

2.2.2估计阶段

指定的响应变量需要通过指定的ARIMA模型来拟合,同时进行该模型的参数估计。模型的适用性需要通过诊断统计量来判断。

考量参数估计值的好坏有几个重要的指标,从多个维度检验估计结果的合理性。

1)模型里各项是否必要通过显著性校验来进行;

2)各模型的优劣通过R2来决定;

3)残差序列所蕴含额外信息通过白噪声残差检验来指明。

经过以上各项检查后,若发现所选模型并不合适,可尝试其他模型,重新开始估计诊断。

3 预测阶段

预测时间序列的未来值,并根据ARIMA模型的预测值生成置信区间如图3所示。

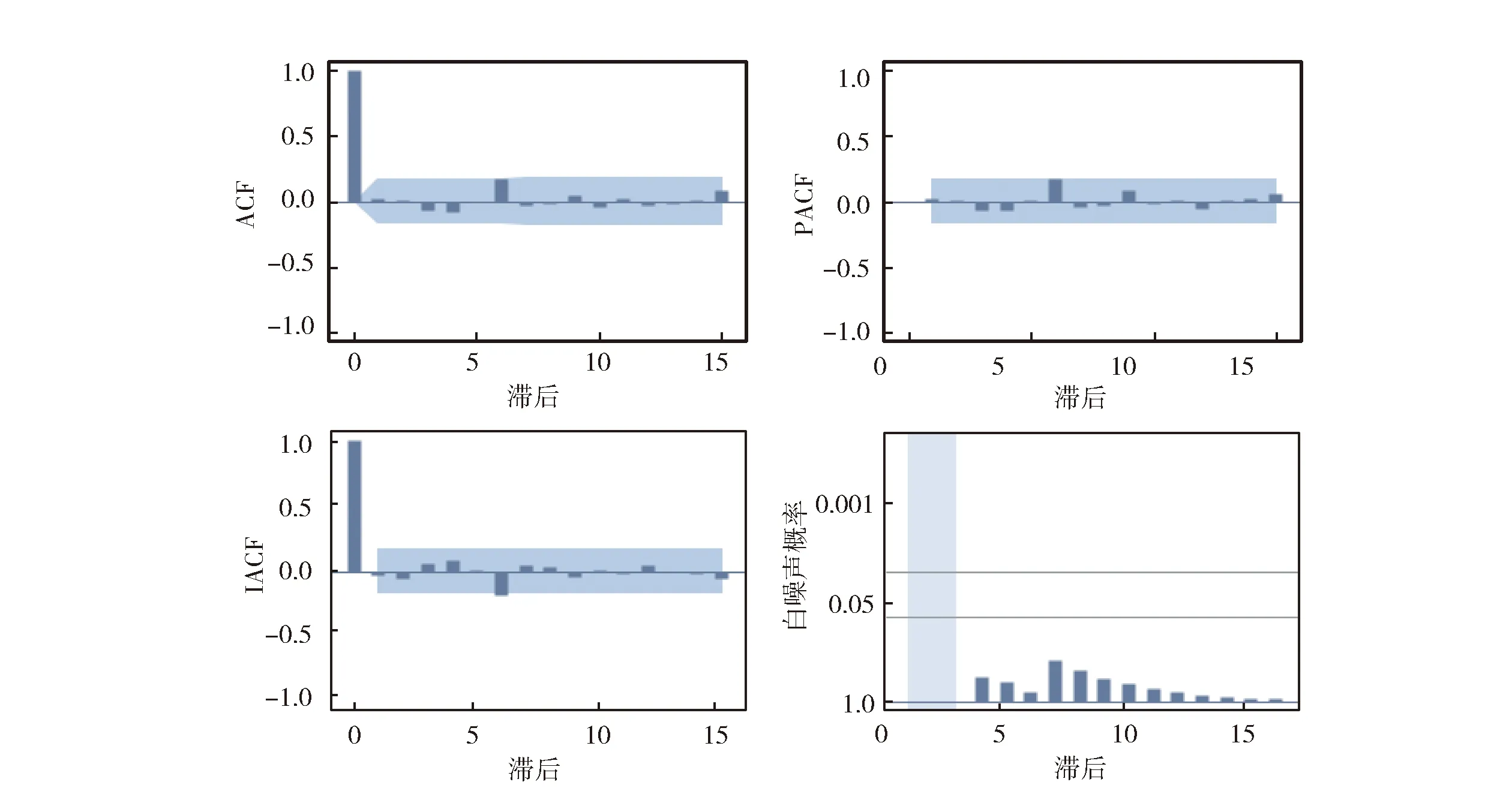
图3 xlog残差相关诊断Fig.3 xlog residual-related diagnosis

图4 xlog残差正态诊断Fig.4 xlog residual normal diagnosis

按AIC和SBC标准计算的统计量,值较小,表明对模型拟合得较好。

另外,从-441.319 5<-438.081 43,-435.569 11<-426.580 65可看出,本次拟合的ARIMA(0,1,1)×(0,1,1)12模型比上次拟合的模型要好。

估计值之间的相关系数为-0.064,这是一个较小的相关系数,如果这个相关系数较大时,就需要考虑是否删除其中一个参数。

对应的QLB统计量分别为6.54和5.60。其所对应的p值分别为0.768和0.231,其所蕴含的信息均已被提取。

最后,如图5所示将表中移动平均MA的两个因子(1-0.50275B)和(1-0.52993B12)代入ARIMA(0,1,1)×(0,1,1)12模型得到:

(1-B)(1-B12)Zt=(1-0.50275B)(1-0.52993B12)εt

其中,Z=log(xt)

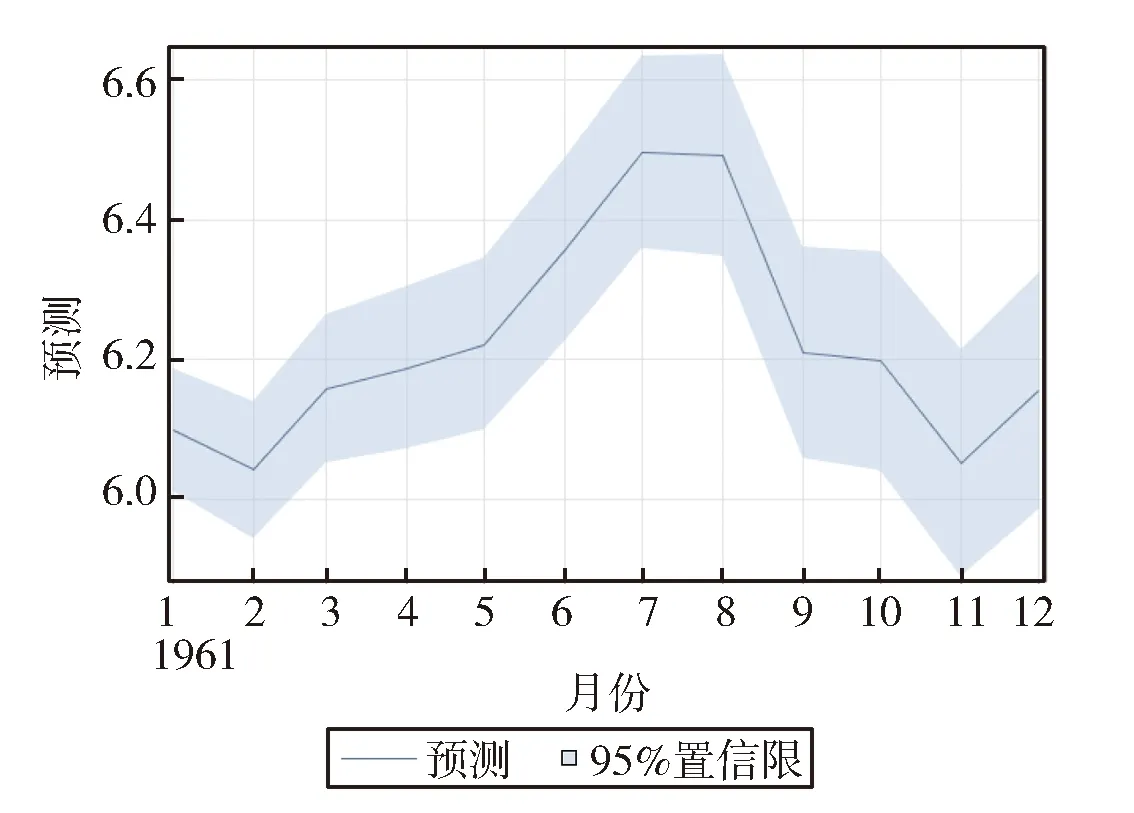
图5 xlog预测Fig.5 xlog prediction

图6 xlog置信度曲线Fig.6 xlog confidence curve

预测今后一年(12期)国际航线各个月度的旅客人数,结果存在数据集forxlog中。

最后,绘制置信度曲线,在图中标注预测数据线和原始数据线的时序图,置信度为95%如图6所示。

4 结语

先验概率的概念一直是贝叶斯统计和非贝叶斯统计的研究热点之一。然而,随着科学的进步,贝叶斯统计在实际应用中的成功已经慢慢改变了人们的看法。贝叶斯统计已经受到人们的重视,成为统计研究的热点。贝叶斯统计推断方法体系是近几十年来迅速发展起来的一种系统建模方法。本文对时间序列预测模型的常用模型进行了深入阐述,提供了标准的建模、估计以及优化思路和流程。在今后的研究工作中,在考虑贝叶斯方法高精度的优势的同时,需要解决贝叶斯估计计算复杂、开销较大的问题。