梳理考点 玩转中考

文龚邦选

实数是各地中考必考内容，其考查要求一般为了解、理解这两个层次，难度系数不大。下面龚老师结合近几年的中考题来和大家一起梳理实数的相关考点，探究解题技法，希望对大家学习实数有所帮助。

考点一 实数的有关概念

1.有理数、无理数、实数的概念

例1 （2015·河南）在实数0，，，-3.140.3030030003…（相邻两个3之间0的个数逐次增加1）中，无理数的个数为（ ）。

A.2 B.3 C.4 D.5

解：，0.3030030003…是无理数，故选B。

评析：辨别有理数与无理数的关键是找准无理数。找准无理数首先要理解无理数的概念，掌握无理数的常见形式。无理数常见的三种形式：开方开不尽的数；（通常）含有π的数；有规律的无限不循环小数。

2.实数的相反数、倒数、绝对值

例2 （1）（2018·南京）的相反

数是____，绝对值是____，倒数是____。

解：（1）的相反数是2，绝对值为2，倒数为-。

评析：有理数的相反数、倒数、绝对值的意义对无理数仍然适用。

3.实数的大小以及与数轴的联系

例3 （1）（2018·南京）下列无理数中，与4最接近的是（ ）。

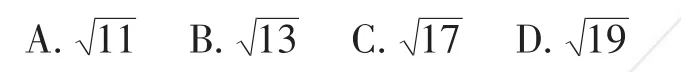
变式1 （2019·南京）下列整数中，与10-最接近的是（ ）。

A.4 B.5 C.6 D.7

变式2 （2017·南京）若，则下列结论中正确的是（ ）。

A.1＜a＜3 B.1＜a＜4

C.2＜a＜3 D.2＜a＜4

解：（1）因为，与16最近的是17，所以与4最近的是，故选C。

变式1：因为9＜13＜16，所以4。又因为3.52=12.25，所以所以与最接近的是6，故选C。

变式2：因为，所以1＜a＜4，故选B。

例4 （1）（2018·建湖一模）已知实数a在数轴上的位置如图1所示，则化简的结果为____________。

图1

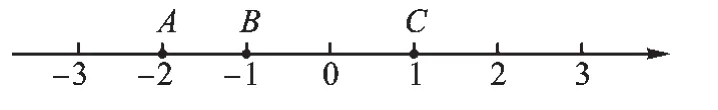
图2

解：（1）原式=1-a-（-a）=1-a+a=1。

评析：要估算一个带根号的无理数的大小，可将根号内的数放在与它相邻的两个平方数之间，即可粗略估算出它的大小。数轴是数形结合的基础，它能把数与直线上的点生动地联系起来。我们在解决实数大小的问题时可借助于数轴。

考点二 实数的运算

例5 （1）（2019·苏州）计算

解：（1）原式=3+2-1=4。

（2）原式=1+4-3+（-3）=-1。

评析：有理数的运算性质、运算律，在实数范围内都仍然适用。在实数范围内，不仅可以进行加、减、乘、除、乘方运算，而且可以进行开立方运算以及非负实数的开平方运算。

考点三 科学记数法与近似数

例6 （1）（2019·南京）2018年，中国与“一带一路”沿线国家货物贸易进口总额达到13000亿美元，用科学记数法表示13000是（ ）。

A.0.13×106B.1.3×104

C.13×103D.130×102

（2）（2016·苏州）肥皂泡的泡壁厚度大约是0.0007mm，可以将0.0007用科学记数法表示为（ ）。

A.0.7×10-3B.7×10-3

C.7×10-4D.7×10-5

（3）（2018·河北）一个整数815550…0用科学记数法表示为8.1555×1010，则原数中的“0”的个数为______。

解：（1）13000=1.3×104，故选B。

（2）把 0.0007 写成 a×10n（1≤ ||a ＜10，n为整数）的形式，其中a=7，n=-4，故选C。

（3）因为 8.1555×1010表示的原数为81555000000，所以原数中的“0”的个数为6。

评析：科学记数法的表示形式为a×10n，其中1≤ ||a ＜10，n为整数。确定n的值时，要看小数点移动了多少位，n的绝对值与小数点移动的位数相同。当原数的绝对值大于1时，n是正数；当原数的绝对值小于1时，n为负数。