含欧拉函数方程φ(mn)=20[φ(m)+φ(n)]的正整数解
(宜春学院 数学与计算机科学学院,江西 宜春 336000)
设Z+为所有正整数构成的数集,φ(m)是Z+上的欧拉函数。关于欧拉函数φ(m)与含欧拉函数的方程,许多学者研究了他们的性质,如1935年ERDÖS[1]研究了欧拉函数的计算与若干性质,提出了含欧拉函数的方程,1981年GUY[2]证明了欧拉函数的加性,1960年 MAKOWSKI[3]讨论了含欧拉函数φ(mn)=φ(m)+φ(n)的正整数解,2010年SUN和CHENG[4]等研究了方程φ(mn)=k[φ(m)+φ(n)]在k为素数时的可解性,张明丽等[5]在2018年讨论了方程φ(mn)=12(φ(m)+φ(n))的正整数解,但漏了许多正整数解,而文献[6-7]也分别研究了一类含欧拉函数的方程的正整数解,得到了较好结果。本文主要研究方程。
φ(mn)=20[φ(m)+φ(n)]
正整数解的存在性等问题,并设计一种有效的初等方法求出了方程在m≤n时的全部119组正整数解,并用此方法可以求出文献[5]中漏了的正整数解。
1 引理
引理1[1]设m=p1α1p2α2…prαr∈Z+,其中pi为互不相同的素数,则
φ(m)=p1α1-1p2α2-1…prαr-1(p1-1)(p2-1)…(pr-1)。
引理2[8]设m∈Z+,若m<3,则φ(m)=1,若m≥3,则φ(m)为偶数。
引理3[9]设m,n∈Z+,且m|n,则φ(m)|φ(n)。

引理5[7]设m∈Z+,则φ(m)=14无正整数解。
2 主要结论
定理含欧拉函数方程φ(mn)=20(φ(m)+φ(n)),当m≤n时共有119组正整数解。
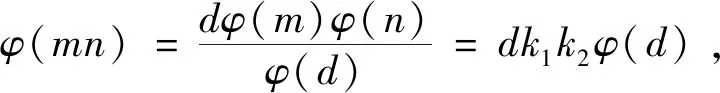
φ(mn)=20(φ(m)+φ(n))=20(k1+k2)φ(d)




















(1)当d=21时,φ(21)=12,k1=1,k2=20,因而φ(m)=12,φ(n)=240,所以方程有正整数解(m,n)=(21,525,)(21,924),(42,525)。
(2)当d=22时,φ(22)=10,k1=1,k2=10,因而φ(m)=10,φ(n)=100,方程无正整数解。
(3)当d=24时,φ(24)=8,k1=1,k2=5,因而φ(m)=8,φ(n)=48,此时方程无正整数解。
(4)当d=25时,φ(25)=20,k1=1,k2=4,因而φ(m)=20,φ(n)=80,此时方程有正整数解(m,n)=(25,200),(25,300)。
(5)当d=30时,φ(30)=8,k1=1,k2=2,因而φ(m)=8,φ(n)=16,此时方程有正整数解(m,n)=(30,60)。
(6)当d=40时,φ(40)=16,k1=1,k2=1,因而φ(m)=16,φ(n)=16,此时方程有正整数解(m,n)=(40,40)。
综上所述,得到了方程φ(mn)=20[φ(m)+φ(n)]在m≤n时的全部119组正整数解。

