一种基于Kriging代理模型的土壤压力沉陷特性预测方法

冯文选，吴大林，马吉胜，何 健

(1.陆军工程大学石家庄校区，河北 石家庄 050003；2.西京学院，陕西 西安 710123)

在车辆地面力学中，土壤作为一种材料，其力学性能是影响履带式自行武器越野行驶性能的重要因素。履带板对土壤施加垂直压力，使土壤在压力作用下产生沉陷，从而影响履带式自行武器的行驶阻力、牵引力和履带板滑转率等性能。在军事行动中，还会影响履带式装备在特定区域的通过性能。因此，研究土壤在垂直压力作用下的沉陷特性对提高武器装备越野行驶性能和通过性意义重大。

由于土壤材料应力应变关系的复杂性，使得通过严格的力学推导来研究土壤承压沉陷特性十分困难。因此，早期的土壤承压沉陷特性研究方法主要以纯经验法和半经验法为主[1]。20世纪70年代，Prumpral J V等首次用非线性弹性问题有限元解法分析了土壤在拖拉机车轮作用下的变形和应力分布。Wong J Y在专著中[2]阐述了土壤应力与破坏的试验观测与有限元法的研究。计算机技术的发展使车辆地面力学的研究方法更加丰富多样，潘卫东等对软地面车辆系统的建模仿真方法进行了研究[3]，吕唯唯等研究了快速加载条件下可变形土壤的特性[4]，赵家丰等研究了重塑土壤压力沉陷特性[5]。

综上所述，在研究方法上，虽然土壤承压沉陷特性的研究手段不断丰富，但以经验法为主的经典土壤承压沉陷特性理论仍然是各国学者开展研究的理论基础。工程实际应用中，经典土壤承压沉陷特性理论需要以大型原位土壤承压试验为依据，由于开展大型原位试验受试验环境、设备和资金等因素的影响，使其存在诸多困难。笔者利用有限元仿真的方法，基于数值拟合方法对土壤压力沉陷特性进行分析，并基于Kriging插值法建立土壤力学参数和加载条件与拟合函数参数之间的关系。

1 土壤本构关系

土壤的应力-应变关系可以用固体力学中的弹塑性理论来描述。土壤的力学行为可以分为弹性行为和塑性行为。弹性行为是土壤在弹性变形范围内的应力-应变关系，可以用弹性本构模型来描述。弹性模型主要包含两个参数，弹性模量E和泊松比μ.常见的土壤弹性本构模型包括线弹性模型、多孔介质弹性模型和线粘弹性模型。笔者采用适用最广泛的各向同性弹性模型描述土壤的弹性行为。

土壤的塑性行为主要包括屈服、硬化、剪胀和流动性，可以用塑性本构模型来描述。经典的土壤塑性本构模型主要有Mohr-Coulomb模型、Drucker-Prager模型和临界状态塑性模型[6]。笔者采用被广泛应用的Mohr-Coulomb模型描述土壤的塑性行为。Mohr-Coulomb模型中的剪切屈服函数为

F=Rmcq-ptanφ-c=0，

(1)

式中：φ为q-p平面上的摩擦角；c为黏聚力；Rmc为屈服函数在π平面上的形状参数。

在ABAQUS软件中，为了避免π平面上屈服面存在尖角导致流动方向不唯一的现象，Mohr-Coulomb模型采用非相关联的流动准则。并通过指定黏聚力c与等效塑性应变之间的关系，控制土壤的硬化规律。

土壤本构参数可以通过土工试验来确定。土体抗剪强度试验是测定土体剪切特性的一种试验，分为室内试验和现场试验。室内试验包括直剪试验和三轴剪切试验，直剪试验仪器设备简单、操作方便、试验用土少，可以测量土壤的抗剪强度参数粘聚力c和内摩擦角φ.三轴压缩试验作为另一种常见的室内土工试验，与直剪试验相比，除了可以测定抗剪强度指标粘聚力c和内摩擦角φ，还可以测定土壤的弹性模量E、泊松比μ和压缩系数等参数[7]。

采用上述两种土工试验对起伏路面松软土壤进行参数测定[8]，得到土壤的力学参数如表1所示。

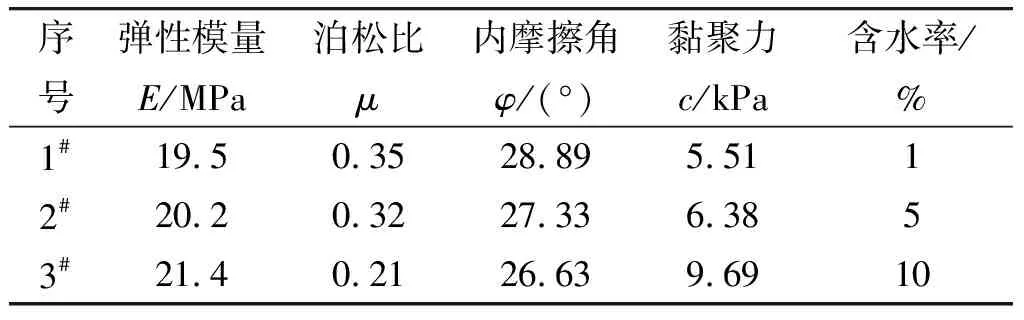
表1 起伏路面土壤力学参数

2 土壤压力沉陷关系非线性拟合

2.1 土壤承压沉陷试验有限元建模

有限元仿真模型采取三维实体建模。载荷板为半径R=0.1 m的圆板。为简化计算，载荷板采用刚体约束，并设置参考点。综合考虑土体模型边界对仿真结果的影响和仿真计算效率，土体采用1 m×1 m×1 m的正方体模型。建立材料分别为钢和土壤的截面属性，钢的材料参数为：密度7 800 kg/m3、弹性模量E=207 GPa、泊松比μ=0.3；土壤本构模型采用各向同性线弹性模型和Mohr-Coulomb模型，参数如表1所示。

约束土体模型4个侧面水平方向位移自由度，底面设置为完全固定约束；约束载荷板参考点水平方向位移自由度和3个方向转动自由度。整个模型采用八节点线性六面体单元，设置减缩积分、沙漏控制和网格重划分区域。土体网格拓扑结构采用中间致密四周相对稀疏的方法。采用显示动态分析步，设置载荷板参考点竖直方向载荷，加载载荷为50 kN，模型装配体如图1所示。

2.2 加载速率对土壤压力沉陷特性的影响

车辆越野行驶过程中，随着车速的不断提高，车辆对地面施加载荷的速率可以达到每秒几兆帕。以美军M4坦克为例，其最大行驶速度42 km/h，总重32 t，平均最大接地压力Pmm=282.2 kPa[9].按照M4坦克履带接地长度为5 m，宽为0.25 m，计算不同行驶速度对应的对地加载速率，如表2所示。

表2 M4坦克行驶速度、加载速率对比

以表2中4种行驶速度所对应的平板加载速率为例，在2.1节建模的基础上，采用表1中2#土壤参数，分别设置不同的加载速率，得到v1～v44种加载速率下的土壤压力沉陷关系曲线，并与准静态加载时的土壤压力沉陷曲线对比，如图2所示。

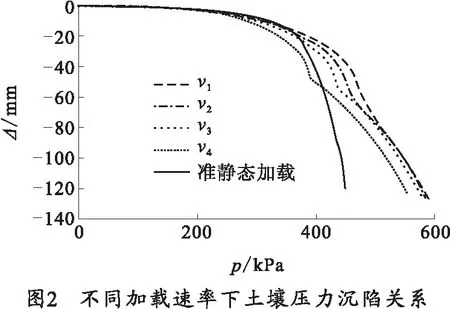
从图2中可以看出，动态加载时的土壤压力沉陷关系与准静态加载时存在明显区别。对照表2中M4坦克行驶速度与加载速率的关系，可以得出：M4坦克行驶速度大于20 km/h时，同一沉陷深度，动态加载条件下的土壤承载力明显高于准静态条件下的土壤承载力。此外，4种加载速率对应的土壤压力沉陷关系之间也存在差异，土壤承载力随着加载速率的增大呈现提高趋势。

2.3 平板尺寸对土壤压力沉陷关系的影响

土壤平板载荷实验中，由于bekker公式所依据的土壤平板载荷试验采用缓慢的加载方式，无法反映土壤在高速载荷作用下的承压沉陷特性，因此有必要研究平板尺寸在高速加载条件下对土壤压力沉陷关系的影响规律。

在2.1节建模的基础上，采用表1中2#土壤参数和表2中v1加载速率，并分别设置平板半径为0.05、0.10、0.15和0.20 m 4种尺寸，得到土壤压力沉陷关系曲线，如图3所示。

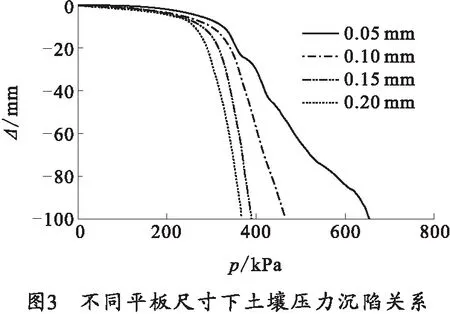
从图3中可以看出，平板尺寸对土壤压力沉陷特性有显著的影响，同一沉陷深度时，土壤承载力随着平板尺寸的增大而减小。且在尺寸越小时，承载力减小的趋势越快。承载力与平板尺寸之间成负相关关系，这一趋势与bekker公式的平板宽度对土壤承载力的影响趋势是一致的。

3 土壤压力沉陷关系拟合

3.1 Prony级数逼近方法

Prony方法是以构造形如式(2)的指数型函数为目的的一种非线性数值逼近算法[10]。

(2)

式中：A，s为待定参数；e为自然底数；t为自变量；f为函数。

Prony方法的主要原理为：令t=iT,使得式(3)成立。

f(iT)=fi，i=0,1,…,2n-1，

(3)

式中：T为步长；{fi}为给定型值。

定义变量zj、αi，且分别满足：

zj=esjT，j=1,…，n,

(4)

(5)

联立式(2)～(5)可得

(6)

zn+αn-1zn-1+…+α1z+α0=0，

(7)

从而求出αi(i=0,1,…,n-1)和Aj.

3.2 数值拟合

以上研究可以得出，土壤的压力沉陷关系属于典型的非线性关系，不仅与土壤的力学性质有关，而且与加载速率和平板尺寸有关。而Prony级数具有良好的非线性逼近能力，因此利用Prony级数，通过MATLAB软件，对不同土壤力学参数和试验条件下的压力沉陷曲线进行拟合。以表1中1#土壤参数为例，在平板尺寸r=0.05 m，加载速率为1 254.22 kPa/s的条件下进行有限元数值仿真，并采用Prony指数函数拟合，如图4所示。

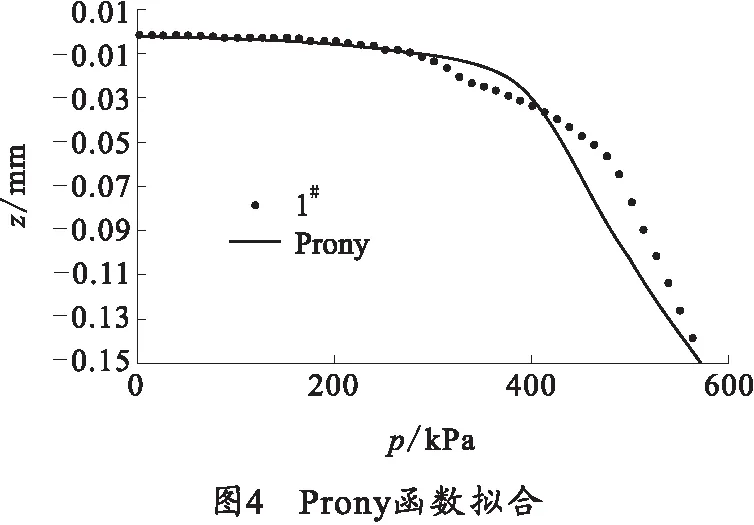
3.3 Kriging代理模型建立

由3.2节可见，Prony级数能够对不同力学性质和试验条件下的土壤压力沉陷曲线进行良好的拟合，且n=2时已具有很高的拟合精度，R2均大于0.9.但是其拟合过程较为复杂，工程实际操作性不强。无法通过已知的土壤力学参数和加载条件直接预测出土壤的压力沉陷特性曲线。而Kriging插值法[11]以变异函数理论与结构分析为基础，在无需确定输入与输出之间精确解析关系的条件下，可以较好的逼近输入与输出参数之间的非线性关系。

以弹性模量E、泊松比μ、内摩擦角φ、黏聚力c、平板半径r和加载速率v为输入参数，以n=2时Prony级数P=aebz+cedz的参数a、b、c、d为输出，建立Kriging代理模型。

输入参数取值范围如表3所示，其中土壤力学参数以起伏路面为参考，平板半径采用小尺寸平板，加载速率以M4坦克20 km/h以上的行驶速度为参考。

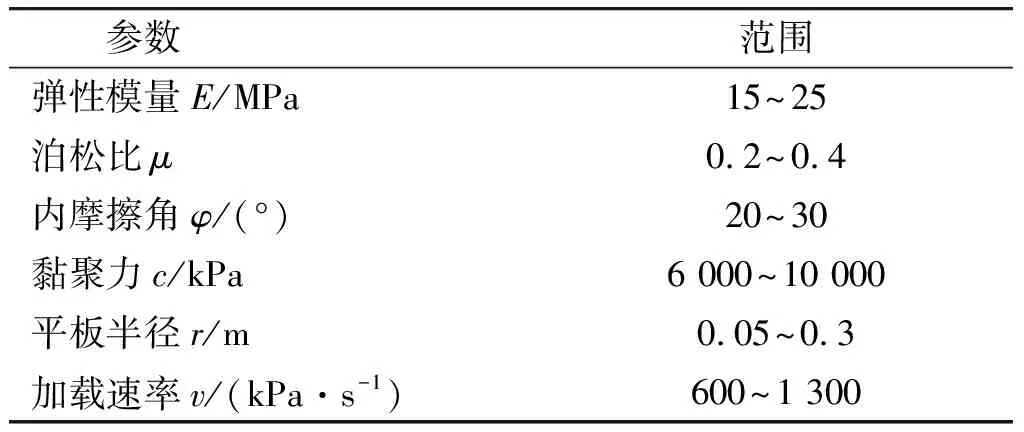
表3 输入参数范围

为使得试验样本尽可能覆盖整个样本空间，采用最优拉丁超立方的方法在样本空间内抽取80组试验样本。基于Isight-Abaqus联合仿真，建立输入参数与输出参数之间的Kriging代理模型。并利用交叉验证的方法对代理模型进行误差分析，得到每个输出参数响应拟合，如图5所示。

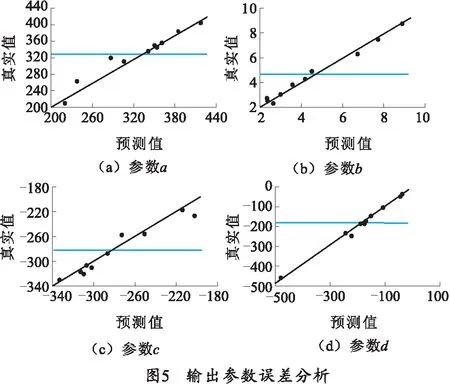
从图5中可得，误差分析样本点对每个输出参数的预测值与真值之间拟合精度良好。通过复相关系数计算，得出各输出参数R2依次为0.96、0.98、0.94、0.99.

3.4 模型测试

利用上述代理模型对起伏路土壤压力沉陷特性进行预测。选取典型试验条件如表4所示。

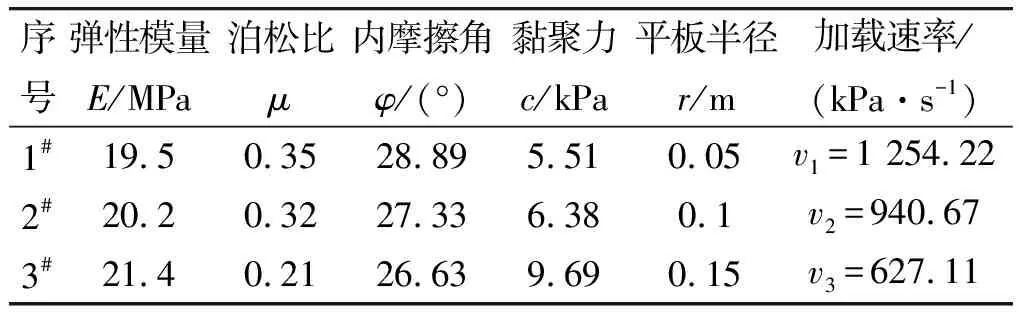
表4 典型土壤压力沉陷试验参数

以表4中3种试验条件为输入参数，得到每种试验条件下的Kriging代理模型输出结果，并把仿真结果和Prony函数拟合结果对比，如图6所示。

从图6中可得，Kriging代理模型对Prony指数函数具有良好的逼近效果，并且能够很好地对不同土壤力学参数和加载条件下的土壤压力沉陷曲线进行拟合。其拟合复相关系数均在0.96以上。

综上所述，Prony指数函数能够对不同加载速率和平板尺寸的土壤压力沉陷特性曲线进行拟合，且拟合精度较高，但是Prony函数在土壤压力沉陷关系拟合中的应用较为繁琐，拟合过程需要依据土壤压力沉陷仿真结果或原位试验结果。以土壤力学参数、加载速率和平板尺寸为输入，以Prony指数函数参数为响应，建立输入与输出之间的Kriging代理模型，可以在不需要仿真和试验的条件下，建立不同土壤力学参数和加载条件下的土壤压力沉陷特性模型，具有一定的工程应用价值。

4 结束语

通过有限元仿真，研究了加载速率和平板尺寸对土壤压力沉陷特性关系的影响。加载速率的提高会增大同一沉陷深度时的土壤承载力，而在仿真范围内，平板半径的增大会导致土壤单位面积承载力的减小。从数值逼近的角度对土壤压力沉陷特性曲线进行了研究，发现Prony指数函数拟合方法可以对不同加载速率和平板尺寸条件下的土壤压力沉陷特性曲线进行拟合，且拟合精度较高。从实际应用的角度出发，采用Kriging插值法建立了土壤力学参数、加载速率和平板尺寸与Prony指数函数参数之间的代理模型，通过输入土壤参数和加载条件可以直接预测特定条件下的土壤压力沉陷特性关系，避免了进行高精度数值仿真和原位试验的过程。对研究土壤承压沉陷特性具有一定的借鉴意义。