地磁信号误差模型分析及补偿算法∗

嵇绍康 高艳丽

（海军航空大学青岛校区航空仪电控制工程与指挥系 青岛 266041）

1 引言

地磁场作为一种重要的地球矢量场，是空间位置与时间的函数［1］。近年来，随着人们对地磁场的不断研究认识，发现利用地磁场进行导航定位有许多其他导航方式不可比拟的优点。其具有的全天时、全天候、全地域、中高精度、高隐蔽性、抗干扰性强的特点［2～4］，使其逐渐成为各国在卫星、潜艇、飞机以及导弹技术领域的研究热点［5～6］。

地磁匹配导航原理图如图1所示。

从图可以看出，地磁导航需要实时获得高精度、高分辨率的地磁场信息，然而，安装在载体上的磁传感器的测量精度受到磁传感器自身测量误差、载体自身的恒磁磁场以及载体上的软磁材料被外界磁场磁化而产生的感应磁场的影响。因而如何准确有效地进行误差补偿是地磁导航需要解决的关键问题。

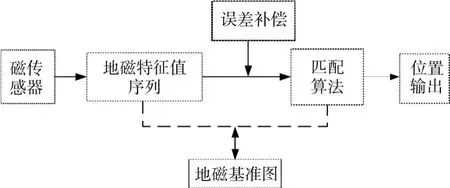
图1 地磁匹配导航原理图

本文首先验证了三轴磁传感器测量值分布于椭球面［7］的特点，在此基础上，通过特定的中心偏移量测量及曲面拟合的平差处理方案求取补偿参数。以往文献［8～9］中直接利用空间椭球面一般方程求解补偿系数的方法忽略了椭球面方程参数之间的相互关系，这使得测量结果不准确。本文采用的方案既可有效地解决上述所列问题，同时也避免了由于数值过大而引起的数值计算问题。

2 信号检测模型分析

2.1 磁传感器自身测量误差组成

仪表测量误差［10］包括：非正交误差、零位和灵敏度误差。

非正交误差是指磁传感器敏感轴非正交而引起的方向测量误差。设o'x'y'z'为理想正交坐标系，由于制造误差而引起的x轴与理想坐标轴的夹角分别为 αx、βx、γx，y轴与理想坐标轴的夹角分别为 αy、βy、γy，z轴与理想坐标轴的夹角分别为αz、βz、γz，则正交误差可表示成

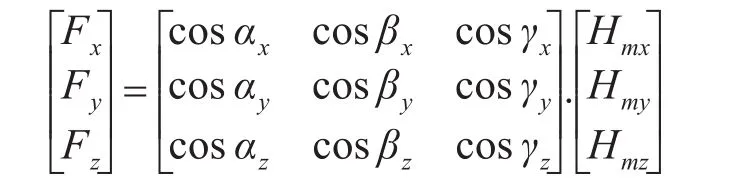
零位误差是因传感器的零点不为零而引起。灵敏度误差是因传感器的灵敏度以及电路放大倍数有差异而引起。记三轴磁传感器在三轴方向上的磁场测量信号的零位分别为Sx0、Sy0和Sz0，灵敏度分别为Lx、Ly和Lz。由上述分析我们可以得出磁传感器测量信号SH与实际地磁背景场之间的关系为

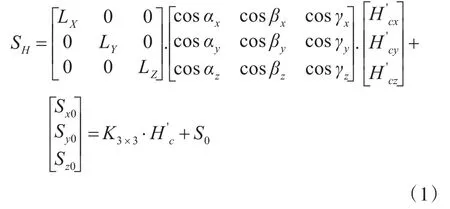
2.2 载体磁场补偿模型

综合考虑各种误差干扰因素我们可得出测量模型为

其中，Hm为软磁材料所受到的外界磁场强度，aij（i，j=1，2，3）为激磁比例系数，该比例系数只和载体的材料与结构有关，为固定值［11］。

设：

模型可转化为

对模型（4）进行变形可以得到：

这里矩阵A为对称矩阵，我们假设它为

将式（8）中的X0看作是三轴磁测量值SH在三维坐标轴内的偏移量，则将磁测量值中心化可得：

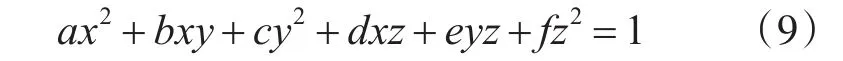
其中 a，b，c，d，e，f为互不影响的参数值。

2.3 干扰模型椭球曲面的验证

已知空间任意位置任意放置的椭球面的参数方程可表示为

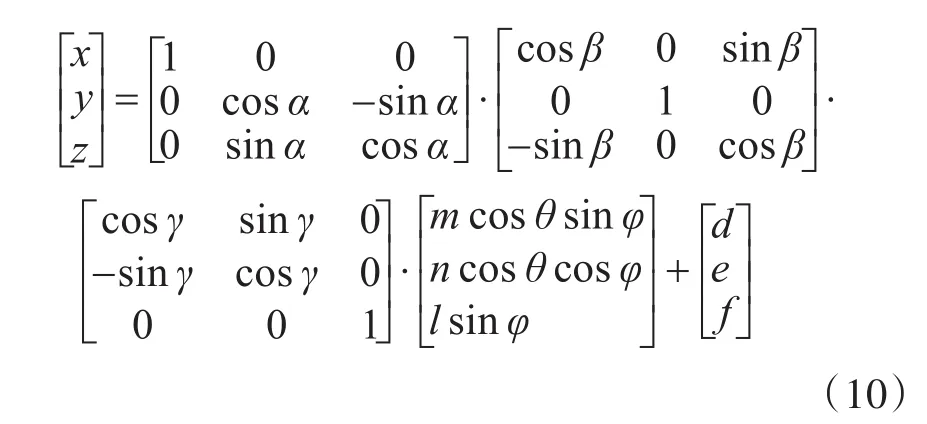
其中，角 α，β，γ为椭球面分别沿x轴、y轴、z轴的旋转角度，矩阵[d e f]T为椭球面中心偏移量。忽略中心偏移量后可得中心位于原点的椭球面参数方程为

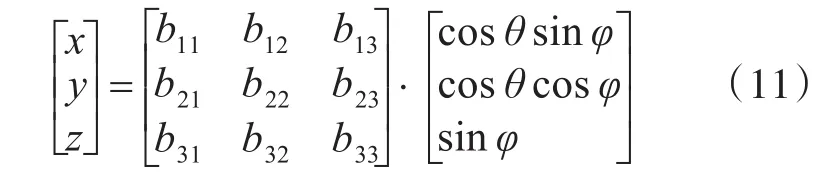
其中，bij（i，j=1，2，3）为含有 α，β，γ，m，n，l六个参量的参数值，分别为

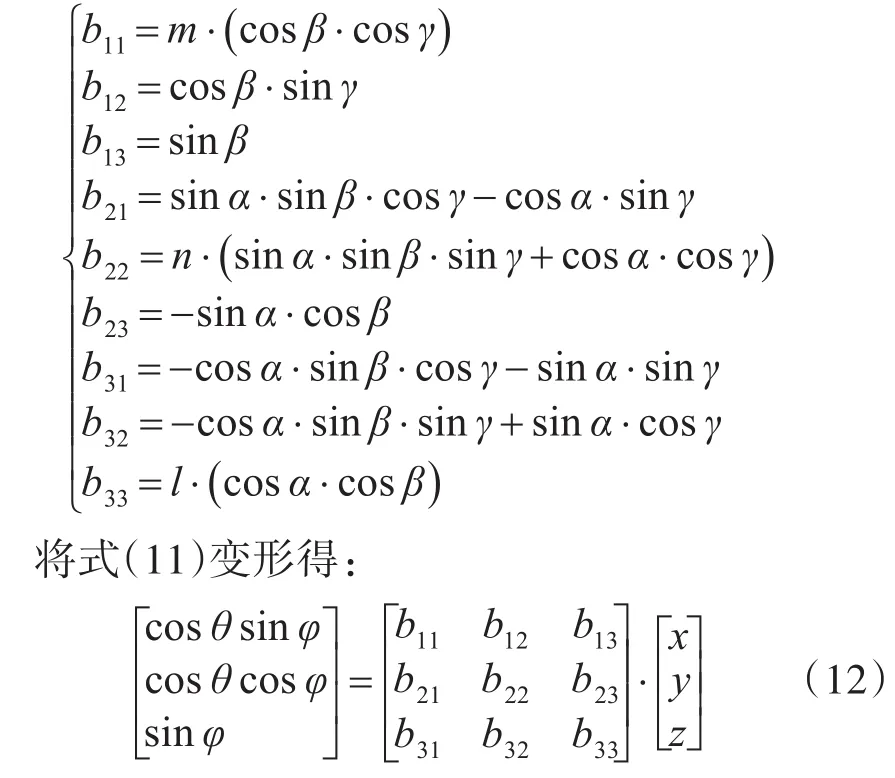
由此，可以得出无中心偏移量的椭球面标准方程为

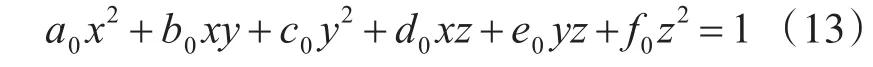
由 于 a0，b0，c0，d0，e0，f0为 含 有 α，β，γ，m，n，l六个参量的互不影响的参数值。

这与三轴磁测量值SH在三维坐标轴内中心化后所得的式（9）对应，因而考虑到偏移量后我们可以得出三轴磁测量值SH分布于空间中具有一定中心偏移量的并且带有一定旋转角度的椭球面上。

3 补偿参数计算方法

本文采用的补偿方案是对平移后的椭球面进行参数求解，由于式（9）中的 a，b，c，d，e，f 为互不影响的参数值，可以利用曲面拟合的最小二乘平差方法对未知参数值进行求解。

3.1 中心偏移量的测量

测量方案如下：

1）数据测量法

通过大量数据的测量求解中心偏移量，这种方法在实际运用方面需要进行大量测量，操作量太大，并且误差大小建立在测量值合适以及数量多少的基础上，一般不予采用。

2）特殊值测量法

选择几组在无磁场干扰情况下测量值正负向反的旋转角度，然后加入干扰量，将三轴转台调到相应角度取测量值的平均值即中心偏移量。然而，由于仪器是三轴磁测量仪，不会出现正负对应的三轴测量值的情况，只有三种特殊情况，即三个轴分别与真实地磁场总强度重合。这样会出现一个量正负相反，另外两个轴量为零的情况。具体测量方法在实验中介绍。

3.2 最小二乘平差法

空间任意位置的椭球面中心化后得到的一般方程为

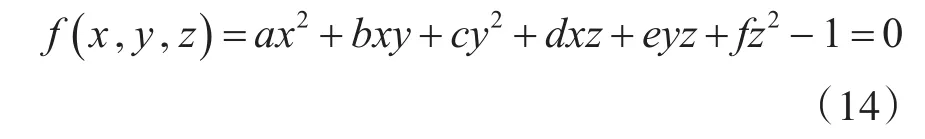
由于观测误差的存在，我们知道观测坐标(xi，yi，zi) 不能都满足式（14），根据最小二乘平差处理方法［12］，我们可得出误差方程如下：

其矩阵形式为：Vi=AiΔa-Li

组成法方程可表示为

式中N=A'TA'，为法方程系系数矩阵，Δa为未知系数矩阵；

其中

由于 a，b，c，d，e，f 相互独立，因此可以直接通过对矩阵求逆得到 a，b，c，d，e，f 的值。

4 实验验证

在实验室环境下，运用无磁三轴转台、FVM-400三轴磁通门磁力仪、铁块和磁铁各一个分别进行测量试验。为验证实验方案有效性，首先需要测得转台所处位置的磁场总强度，我们应用高精度测量仪测得数值大约为52520nT。

首先调整转台三轴方位归0，将磁力仪安装于三轴转台工作台面中心位置，记录下转台不受干扰影响时的三轴测量值分别为［-40721；20085；22387］，取8种转台姿态，记录下不同姿态时的地磁场三分量。然后，在三轴转台上分别安装铁块和磁铁作为地磁测量干扰源，调整三轴转台处于我们选取的8种对应姿态，分别记录转台在不同姿态下磁力仪的三轴分量，将上述8组实验数据列于表1。

表1 实验数据

利用三轴坐标系转换关系：

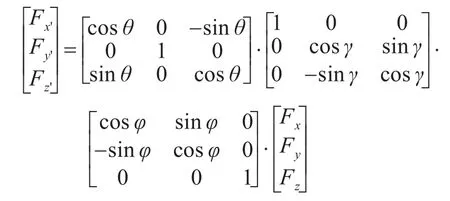
进一步，变换旋转角度分别为：[- 2 6.253°，0°，26.3°][63.75°， -153.7°，0°] [6 3 .75°，116.25°，0°] 可 使 x 轴 、y轴、z轴分别与真实地磁场负方向重合，分别测量安装上铁块和磁铁时上述6种旋转状态的3轴测量值，取平均值可得中心偏移量：X0=[4 84.13 182.83 90.47]T。

将表1中受干扰影响的8种测量量中心化后，用最小二乘平差处理方法计算得到：

将安装有铁块和磁铁的转台处于表2的6种姿态下，记录下三轴测量值，总场强值记录于表2中，通过式（6）以及求得的补偿参数对这6种状态值进行补偿求解，校准后数据列于表2中。从表2中可以看出校准后的磁场测量值比校准前的数据在精度提高了很多，更接近于真实地磁场强度。

表2 校准前后测量数据比较

5 结语

本文对磁传感器检测系统误差模型以及三维椭球面参数方程分析验证，确定了三轴磁测量值空间分布特点。通过实验测量与数值计算得到补偿参数，运用数据验证补偿方案，实验表明：该方案对磁传感仪周围软硬磁干扰所引起的误差有很好的抑制效果。

文章在计算中心偏移量时，由于初始状态的测量值是包含有测量仪器自身误差的测量值，因而所计算的转台旋转角度存在有一定误差，正确方法是对三轴磁测量仪进行标定处理，求得仪器自身误差参数，然后利用标定处理后的初始状态数据进行旋转角度求解。由于实验器材的限制，未能对其进行适当处理，这是下一步有待解决的问题。