一道考题引起的思考

万凡

【中图分类号】G623.5 【文献标识码】A 【文章编号】2095-3089（2019）48-0139-02

三年级期末检测的试卷时，发现这样一道比较大小的题目：7÷4○77÷44，很多学生都填的“<”，明明是相等，为什么这么多同学填小于呢？带着这个疑问，向三年级任教老师探讨，任教老师说，三年级学生还没有学习小数的除法，平日里都是这样告诉学生，如果比较两个除法算式的大小，要先比商，商大的就大;如果商一样，比余数，余数大的就大。

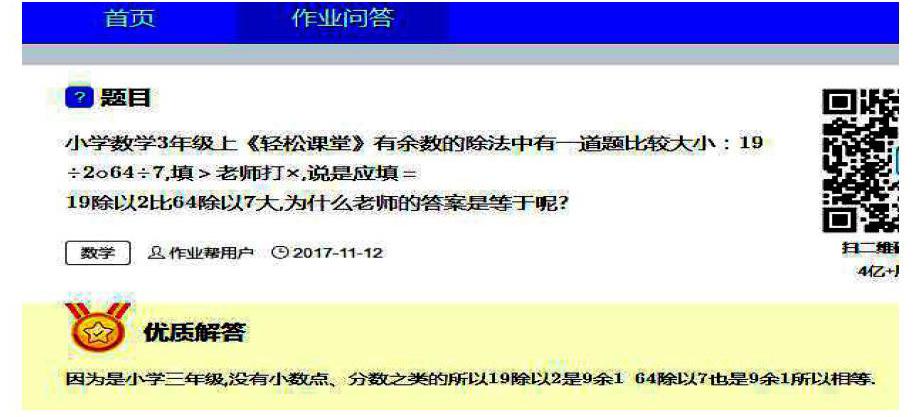
听完任课老师的解答，心中还是有些困惑，带着这样的困惑，去百度了一下，无独有偶，百度中也有这样一道类似的题目：

或许，这位老师也是根据两道算式19÷2=9……1和64÷7=9……1的商一样，余数也一样就得出相等的结论的吧！

但心中困惑并没解除，我想，虽然三年级学生没有学习小数除法，但我能不能试着利用学生在二年级已经学习过的商和余数的意义及三年级学习的分数相关知识来解释这两道题的正确答案呢？

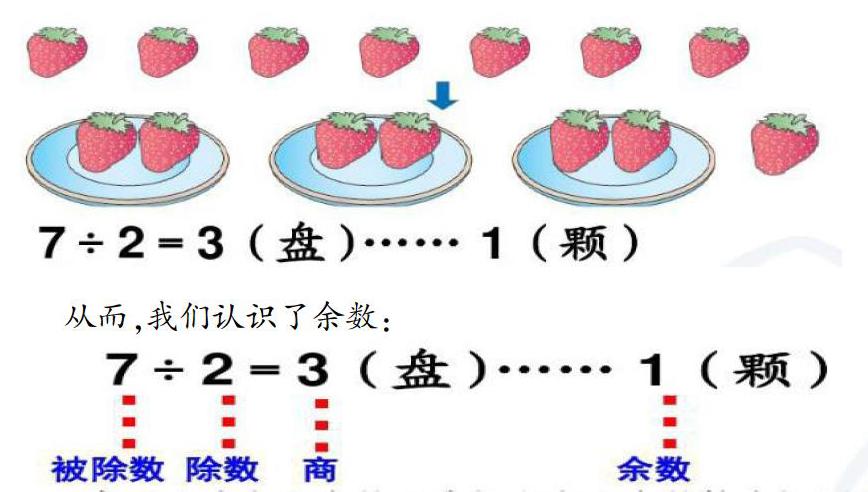
二年级的学生初次学习有余数的除法时，是通过摆一摆的方式来认识余数的：6颗草莓，每两个摆一盘，看看能摆几盘？如果不是6颗草莓，而是7颗草莓，每两个摆一盘，能摆几盘？

从而，我们认识了余数：

也就是说，两颗草莓是一份，可以摆3份还剩1颗，这1颗草莓就是余数，因为这1颗草莓不是一份，但根据学过的分数知识来看，这1颗草莓其实表示的是半份即1/2，所以余数的意义也可以用分数来表示。

所以，再来看前面提到的考题：7÷4○77÷44。

7÷4=1……3，77÷44=1……33，前面算式中的余数3的意义用分数来表示即是3/4，后面算式中余数33的意义用分数来表示也是3/4，学生可能不明白，我们可以这样解释：除数是44，余数是33，还差11就可以表示一份，33里面有3个11，分数表示也是3/4，所以7÷4=77÷44。

同样的道理，也能比較出19÷2和64÷7的大小。19÷2=9……1，余数1用分数表示1/2，64÷7=9……1，这道算式中的余数1分数表示是1/7，1/2是大于1/7的，所以前者算式大于后者算式。

因此，我们在比较有余数的除法算式大小时，不能说商一样，余数大的就大，还要看除数的大小。

前苏联教育家维果茨基提出过最近发展区理论：他认为学生的发展有两种水平：一种是已经达到的发展水平;另一种是儿童可能达到的发展水平，表现为“儿童还不能独立地完成任务，但在成人的帮助下，在集体活动中，通过模仿，却能够完成这些任务”。这两种水平之间的距离，就是“最近发展区”。所谓可能发展区，维果茨基的说法，是介于儿童自己实力所能达到的水平（如学业成就），与经别人给予协助后所可能达到的水平，两种水平之间有一段差距，即为该儿童的可能发展区。

我想，在我们的教学中，也应该找到儿童的最近发展区，在教师的协助下，让学生达到可能更高的水平。