浅谈泰勒公式在高考数学压轴题中的应用

孙玉静

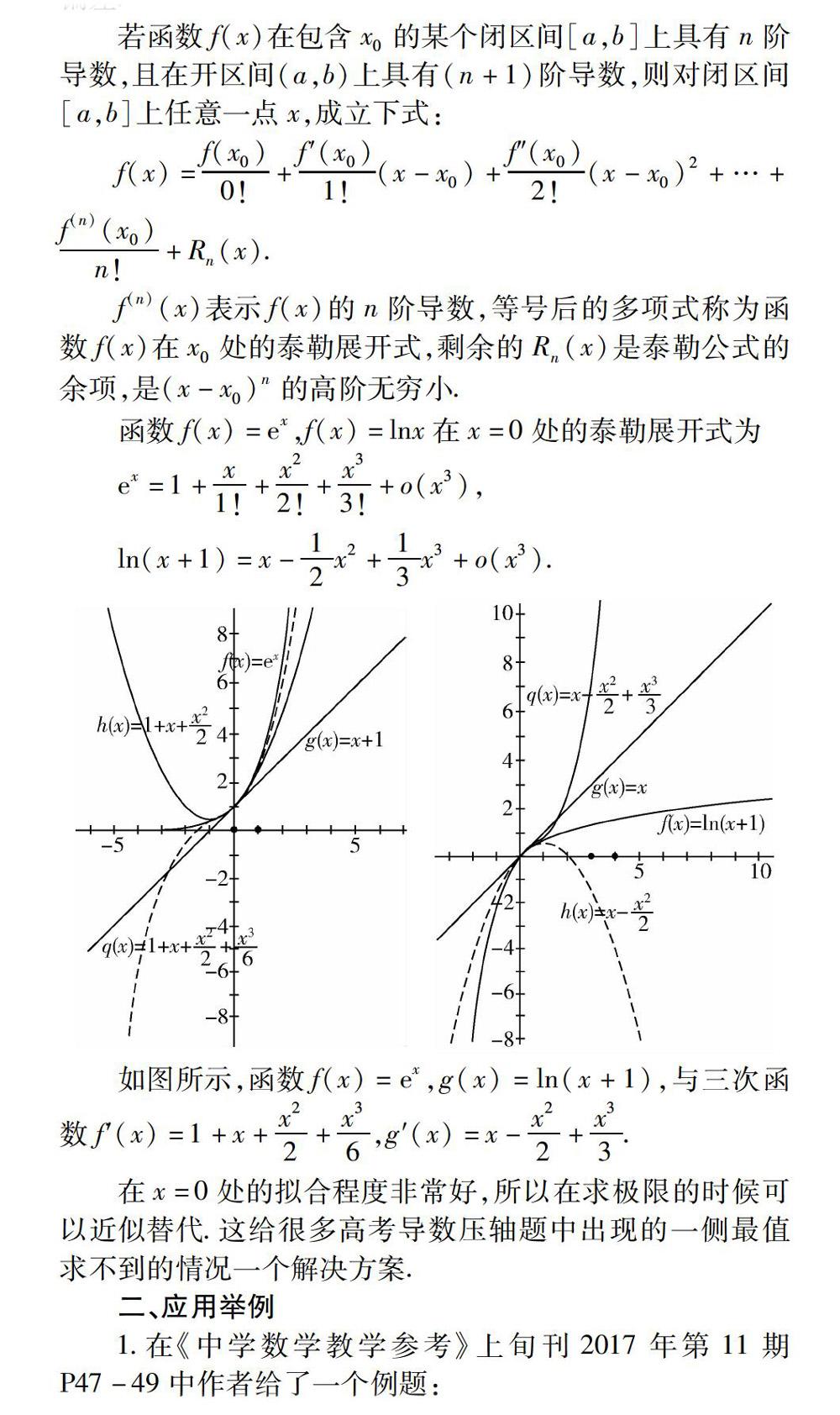
近年来，在各类测试和高考命题中，不等式ex≥x+1，lnx≤x-1都是出题者出题的一个很重要的出发点.上面的两个不等式都是很容易证明的，追根溯源，这两个不等式都来源于高等数学中的泰勒展开公式.本文在简单介绍泰勒公式的基础上，结合例题给大家呈现函数y=ex，y=lnx的泰勒公式在高考压轴题中的应用.

一、背景介绍

数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式.如果函数足够平滑的话，在已知函数在某一点的各阶导数值的情况下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值.泰勒公式还给出了这个多项式和实际的函数值之间的偏差.

三、备考启示

1.随着向量，算法，概率统计，导数等原来在大学才接触的知识渗透到高中教材，高考作为选拔性的考试，试卷中也经常出现以高等数学为背景的试题.这类题目往往就是考查学生的知识迁移能力，综合分析解决问题的能力，所以我们高中教师要更注意培养学生的数学思维能力及数学学科素养.

2.培养学生的认知能力.就是不光要教会学生如何应对考试中的各种题型，而且要培养学生站在出题者的高度去思考他们会从哪些角度出题.这就要求我们高中教师要用新课程标准审视常规教学，提高自己的教育科研能力，注重“高观点”下的中学数学衔接问题.

3.从简单到复杂，从直观到抽象是学生学习的基本认知规律，所以有一些抽象的代数问题如果能以数形结合的方式帮助学生理解，学生的学习效果肯定会更好.这就要求我们教师要注意信息技术的应用.在教学中更多地运用数学学习心理学原理来更好的规划课堂.

【参考文献】

[1]范东晖.入乎其内，出乎其外——让习题教学更有效[J].中学数学教学参考，2017（11）：47-49.

[2]曹世鵬.以高等数学为背景的高考数学试题的研究[J].中学数学研究，2016（6）：17-20.