豪泰林模型下的价格竞争和选址
(北京物资学院 北京 101199)
一、豪泰林模型价格竞争
(一)豪泰林模型的基本假设
假定长度为1,消费者密度为1的均匀分布“线性城市”,每个消费者购买一个单位的商品。该城市有两家企业销售同质商品,引入旅行成本,两企业产品之间的替代弹性不是无限的,消费者对不同的企业产品的偏好不同,价格不是唯一的参考变量。假定企业1位于a≥0,企业2位于1-b(b≥0),1-a-b≥0(即商店1位于商店2的左边)。旅行成本为二次式,即旅行成本为td2。
(二)模型的建立和求解
两个企业同时选择自己的价格,考察价格的纳什均衡。令pi为商品i的价格,Di(p1,p2)为需求函数,i=1,2。商品1的需求函数:D1=x商品2的需求函数:D2=1-x。
p1+t(x-a)2=p2+t(1-b-x)2
需求函数为:
利润函数为:
π1(p1,p2)=(p1-c)D1(p1,p2)
π2(p1,p2)=(p2-c)D2(p1,p2)
在给定另一个企业的价格情况下选择自己的价格,一阶条件分别是:
满足二阶条件,纳什均衡为:
此处,我们把旅行成本带来的产品价格差异称之为产品差异,即使是完全同质的产品,差异性越高,即旅行成本越高,均衡价格和均衡利润越高。商品的替代率随着旅行成本的升高而降低,每个企业对附近的消费者垄断程度提高,企业之间的竞争减弱。另一方面,当旅行成本为0时,不同企业之间的产品具有完全替代性,即价格等于成本,也就是我们的伯川德均衡结果。
图形表示以及动态解释:
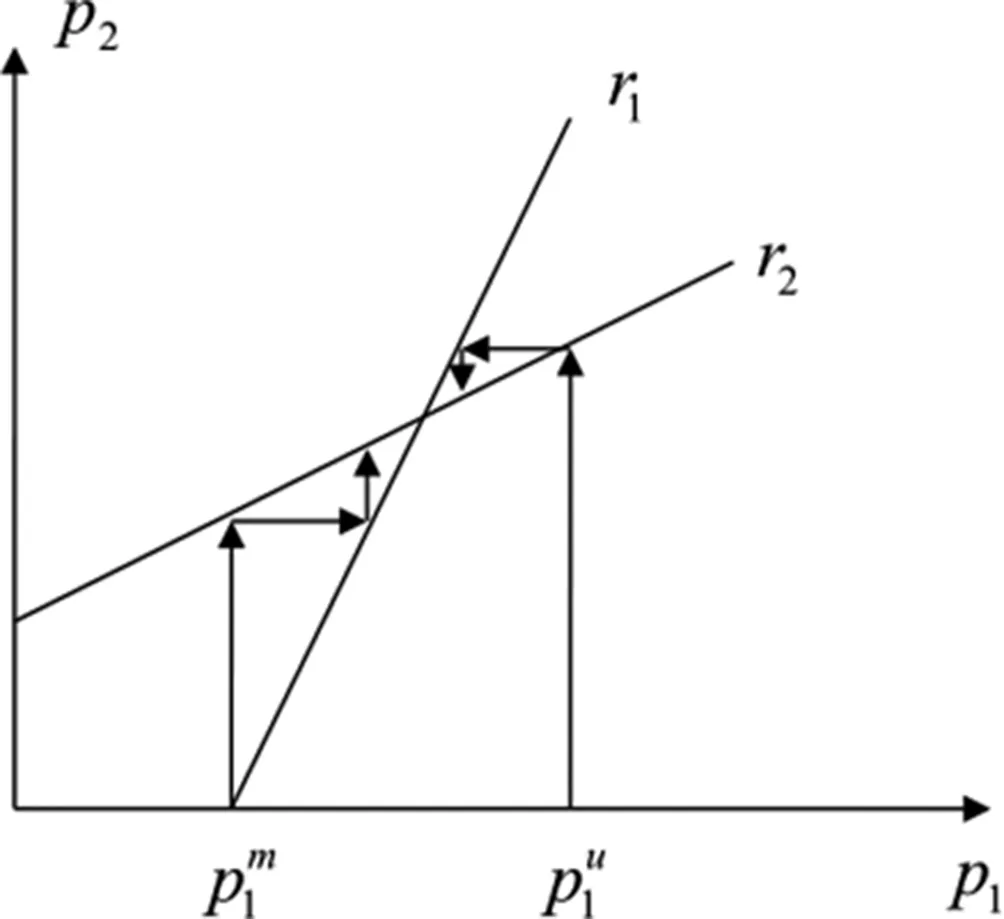
利用重复剔除严格劣策略的方法解释为:
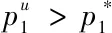
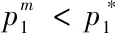
考虑产品差异的情况下,企业的价格策略途径如图所示,最终在均衡价格处达到均衡。而不考虑产品差异的情况下,也即旅行成本为0,消费者关心的只有产品价格,产品是完全替代的,消费者选择哪个企业的产品是完全无差异的,此时的均衡利润为0。
二、豪泰林模型的企业选址
企业为了实现利润最大化,就要通过选址策略来增强对附近消费者的垄断程度,从而最大化额外利润。两个企业在选址过程中,同时选择地址,地址选定之后,根据前面的分析,我们可以利用利润函数来研究企业的需求函数。
π1(a,b)=[p1(a,b)-c]D1[a,b,p1(a,b),p2(a,b)]
π2(a,b)=[p2(a,b)-c]D2[a,b,p1(a,b),p2(a,b)]
以π1为例,一阶化条件:
根据上一部分的分析可知:
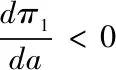
结论分析
1.由以上结果可以看出,企业的垄断利润是关于a的单调递减函数,即a越大,企业的额外利润越低,当a=1-b时,得到伯川德均衡结果,也就是利润的最小值0,当a=0时,得到最大的额外利润t/2。所以,两个企业总是倾向于往两边移动。当b 2.从社会福利最大化的角度,由于消费者数量和消费数量固定,且消费者平均分布在“线性城市”,所以社会监管者根据消费平均成本最小化原则,以及对称性原则,选择把两家企业分布在中心位置两边等间距的地方,从而使得每一家企业以同样的价格供应两侧的消费者。

