基于股票收益率的ARIMA财务风险预警模型
(华南理工大学 广东 广州 510006)
一、ARIMA模型
商业,经济,环境,医学和其他科学领域的时间序列数据往往表现出趋势,季节性波动、不规则周期以及偶尔的水平或变异性变化等模式。分析此类序列的目的通常是推断数据中的动态模式,以预测未来的观察结果,估计已知外源性干预措施的效果,并检测未预料到的干预措施。本文概述了实现这些目标的一些有用方法。时间序列数据中的序列依赖性通常可以通过线性动态模型充分近似。许多观察到的时间序列是非平稳的,通常表现出趋势,可能以多种形式出现。通常可以通过将数据差分适当的次数来消除这种趋势,在这种情况下,该系列被称为集成过程。然后,通过均匀非平稳性的概念,这导致自回归-积分-移动平均(ARIMA)过程,将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归。混合自回归滑动平均(ARMA)模型,广泛用于表示静止和非平稳系列。对于单位根非平稳性,这导致了一类自回归整合移动平均(ARIMA)模型。Box和Jenkins提出的迭代模型构建方法由临时模型规范,有效估计和诊断检查组成,由一个实际例子进行讨论和说明。
二、研究内容和研究意义
以“佳讯飞鸿”2015年到2017年每日的股票收益率作为时间序列的分析数据,参考已有的研究文献,从平稳性检验和数据预处理、模型识别(识别AR模型的阶数(p),识别MA模型的顺序(q))、参数估计、模型拟合优度、模型预测等5个方面,构建股票收益率的ARIMA(p,d,q)模型。采用构建的ARIMA模型对“佳讯飞鸿”的日股票收益率进行预测,一方面更好地反映其股票收益率的动态变化,从而进行风险管理;另一方面为在无法根据历史信息实现超额利润,历史数据就会具有较强的预测能力的弱势有效的股票市场的量化投资提供较大的应用价值,促进股票金融市场的理性投资。
三、文献综述
万建强,文洲(2001)[1]认为ARCH模型和ARMA模型在应用中并不存在绝对的优劣选择,只是不同时期的股价波动率不同导致的拟合优度的更佳。
刘美霞(2011)[2]以2009年7月1日到2010年6月30日的每日深证指数收盘价格为原始数据,通过对数据进行平稳、零均值化处理,模型识别和模型定阶,再使用最小二乘法估计参数后,最终建立了ARIMA(6,1,6)模型,并对模型检验证明有效后,对未来数据进行了短期预测。
代聪文(2011)[3]分别采用了ARIMA和灰色预测法对甘肃省的能源消耗进行建模和分析。组合预测结果的相对误差小于以上两个单独模型的相对误差,精度要高于单一模型。
卢怀营(2013)[4]运用2010年5月7日至2013年2月22日的时间序列数据,建立了沪深300指数的ARIMA预测模型,并对模型的预测效果进行了分析。并根据得到的结论构建ETF基金对沪深300指数进行期现套利。
夏丽(2013)[5]研究基于用电量的时间序列数据构建ARIMA模型进行短期预测,利用粗糙集理论对时序数据进行预处理,提高了ARIMA模型预测的精度。
袁磊(2015)[6]ARIMA模型是使用最广泛的线性模型,结合LSSVM解决非线性回归的问题,实证结论表明ARIMA-LSSVM的混合模型的预测性能比单一的模型、传统的混合模型预测效果更好。
王永斌、郑瑶、柴峰、李向文、田珍榛、袁聚祥(2015)[7]利用2004年1月-2014年12月我国甲肝月发病率资料,构建ARIMA模型和SARIMA模型基于周期分解的ARIMA模型拟合和预测效果优于SARIMA模型。
简琦琛(2017)[8]构建了基于ARIMA的数据学习预测模型,对企业生产中的生产计划的制订、原材料的采购和库存等供应链的过程进行精细化的预测。
葛娜、孙连英、赵平、万莹(2018)[9]以ARIMA模型对商业经营问题中的销售建立预测模型,从数据检验及预处理、模型识别与定阶、参数估计、模型适应性检验、模型预测和误差分析6个方面对构建模型来解释预测销售量值与记录值之间的关系。
管超宇(2018)[10]搜集浙江省1986-2017年GDP的数据进行分析,构建ARIMA模型对接下来今年浙江省的GDP进行预测,对经济发展起到很好的帮助。
综合以上2001年到2018年的学者的文献研究,可以发现ARIMA模型的应用越来越广泛,由原来的单一模型的预测扩展到了多元混合模型的预测,在股票市场、能源行业和生产消费行业都有较大的应用价值。
四、数据来源
以“佳讯飞鸿”为研究标的,从同花顺交易软件下载2015年1月1日-2017年12月29日的每日交易开盘价和收盘价,然后对日收益率进行对数处理,总共有782个交易日收益率数据。
五、模型构建
平稳性检验是对数据进行回归的重要检验环节,如果数据不满足平稳性检验,会出现随机趋势或确定趋势导致的伪回归的现象,统计意义并不明显。常见的检验平稳性的检验方法有单位根检验和ADF检验,拒绝原假设,则为平稳数据,满足平稳性。
(一)平稳性检验

表1 ADF测试
P值为0.00,拒绝原假设,数据为平稳数据。
原始数据的ACF和PACF都是拖尾的,因此,可对原始序列(是原始序列)建立ARMA(p,q)模型我们可以观察这些图并得出自回归(AR)和移动平均(MA)。我们知道,对于AR模型,PACF将呈指数衰减,PACF图将用于识别AR模型的阶数(p)。对于MA模型,ACF将以指数方式衰减,ACF图将用于识别MA模型的顺序(q)。原始数据的ACF、PACF在第11阶的时候落在2倍标准差的边缘,很难使用传统方法确定阶数,本例通过反复对模型进行估计比较不同模型变量对应参数的显著性来确定模型阶数。
(二)模型参数估计
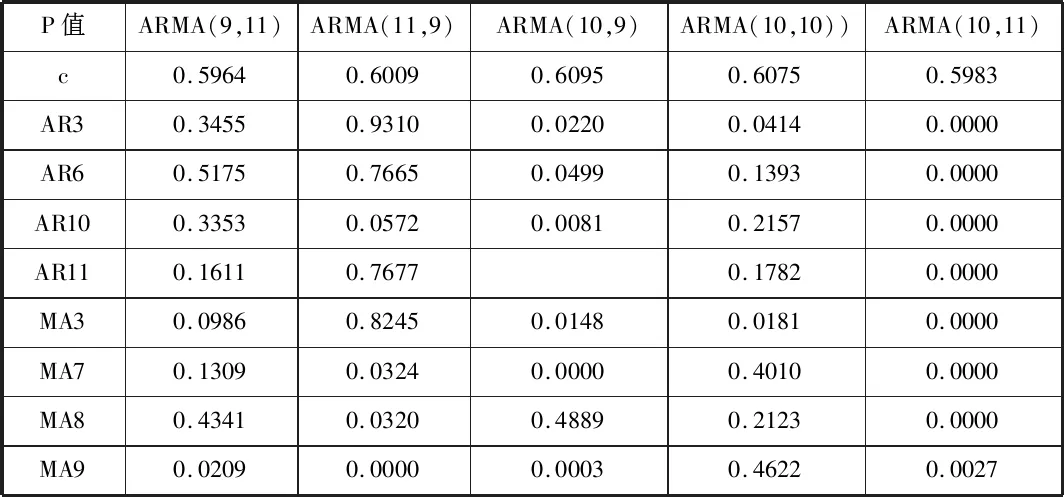
表2 模型参数比较
标黄的为0或接近于0的P值。通过对多个模型进行反复比较,发现只有ARMA(10,9)和ARMA(10,11)的参数估计值几乎全部显著。下面利用AIC信息准则对ARMA(9,11)、ARMA(11,9)、ARMA(10,10)、ARMA(10,9)、ARMA(10,11)进行模型的筛选。

表3 模型的AIC和BIC值
从表3的模型的AIC的比较值可以发现ARMA(10,11)的AIC值为最小,是比较适合的模型。ARMA(10,0,11)的各项参数估计值在0.01的水平下是显著的。对残差进行自相关检验,残差小于0.01,接近于0,不存在ARCH效应,因此模型是比较合适的模型。可得ARMA(10,0,11)模型为
Yt=-0.7432Y(t-1)-0.9103Y(t-2)-1.62663Y(t-3)-1.4075Y(t-4)-1.7548Y(t-5)-1.3845Y(t-6)-0.7002Y(t-7)-0.6142Y(t-8)-0.6142Y(t-9)-0.808Y(t-10)+0.8064∂(t-1)+0.9606∂(t-2)+1.7381∂(t-3)+1.5581∂(t-4)+1.9708∂(t-5)+1.6249∂(t-6)+1.576∂(t-7)+0.9462∂(t-8)+0.7187∂(t-9)+0.9247∂(t-10)+0.095∂(t-11)-0.0005
(三)模型预测
样本范围内(2015-2017)的序列是已知的,因此,动态预测只是适应于样本外(2017-2018)预测,样本内(2015-2017)采用静态预测。样本内静态预测和样本外的动态预测拟合效果良好。
六、结论
本文在同花顺网站上收集2015年1月1日至2017年12月29日的佳讯飞鸿的每日收盘价,得到每日收益率数据,然后对数化处理。对每日收益率数据利用ARIMA(p,d,q)模型进行分析,通过平稳性检验,ADF检验,AIC准则,拟合预测,说明模型拟合效果较好,预测趋势大致一致。目前,股票市场逐渐复苏,随着股票市场相关市场机制的完善,政府政策以及监管机构的调控,股票市场会逐渐走向更为理性的投资。对股票收益率的预测可以有效地进行风险预警和风险管理。

