管线腐蚀的切向投影等效面积因子描述方法

(滨州学院 化工与安全学院，滨州 256600)

油气管道是油气生产、加工与输运的命脉。根据2016年北美管线失效原因统计可知[1]，截致2016年,北美管道事故原因前三位分别为：腐蚀和应力腐蚀(占42%)，第三方损害(占23%)以及自然荷载(占19%)。2015年中国陆上油气管道总里程超过12万km，每年因腐蚀导致的管线维修、更换、报废造成的经济浪费和损失巨大。

国内腐蚀管线剩余强度评价方法多以美国机械工程师协会(ASEM)推出的ASME B31G系列标准[2-3]为依据。中国科学院金属研究所国家金属腐蚀控制工程技术研究中心韩恩厚提出了腐蚀裂纹当量法，首次把断裂力学引入到腐蚀管线剩余强度的计算中，编写了我国第一部管道腐蚀损伤评价石油行业推荐标准即《钢质管道管体腐蚀损伤评价方法》SY/T 6151-2009[4]。表1列出了国内外应用较广泛的腐蚀管道剩余强度评价规范。其中ASME B31G-1984、ASME B31G-1991和我国的SY/T 6151-2009标准涉及到了腐蚀切向投影等效面积因子(以下简称等效面积因子)的计算，1991年美国机械工程师协会专门修改了ASME B31G-1984标准中等效面积因子，形成了ASME B31G-1991标准，可见其对管线剩余强度计算方法的影响之大。SY/T 6151-2009标准中还涉及到材料裂纹张开位移(COD)临界值的试验测试，由于试验难度较大，故不适合现场工程应用，其他两种标准均默认为腐蚀切向投影为矩形，且形状对失效压力计算方法的影响不大，因此本工作重点分析了ASME B31G-1991、ASME B31G-2009、ASME B31G-2012中涉及的等效面积因子对管道剩余强度的影响。

表1 五种常用评价规范中失效压力计算方法Tab. 1 Calculating methods for failure pressure in five common standards

表1中：σs为管材的屈服强度，MPa；σb为管材的抗拉强度，MPa；a为腐蚀深度，mm；pf为管道的失效压力，MPa；t为管壁厚度，mm；L为腐蚀长度，mm；D为管道外直径，mm；M为Folias系数；σflow为管材的流变应力，MPa；R1为管道内半径，mm；R2为管道外半径，mm；Q为长度校正系数；E为弹性模量。在实际工况条件下,管线腐蚀缺陷的轴向投影往往是不规则的，如图1所示。目前,广泛采用的管线内腐蚀检测方法是漏磁技术，该方法在常规情况下只能检测出腐蚀的长度、深度以及宽度，无法给出腐蚀的具体形貌，因此，需要采用合适的方法描述腐蚀形貌。本工作针对延长油气田已有的上百处腐蚀缺陷，应用统计分析方法尽可能准确地描述这些腐蚀形貌。

图1 管线腐蚀缺陷形貌Fig. 1 Morphology of corrosion defects on pipeline

1 实际面积因子的影响

研究采用ANSYS软件分析具有不同实际腐蚀切向投影面积因子(简称实际面积因子)腐蚀管道的失效压力，关于数值模拟过程中网格无关性验证以及ANSYS非线性有限元分析方法的准确性和适应性已在文献[7-8]中做了充分证明，在此不再赘述。研究以X65管线钢为对象，其性能参数如表2所示。

表2 X65管线钢性能参数Tab. 2 X65 pipeline steel performance parameters

假设X65管线钢的应力-应变关系符合文献[9-12]所描述的幂硬化应力-应变法则，具有不同实际面积因子的腐蚀管道模型如图2所示，在采用的ANSYS非线性有限元分析模型中实际面积因子互不相同。

计算分析了46组具有不同腐蚀深度、腐蚀长度、实际面积因子的管道失效压力。将已知的实际面积因子代替等效面积因子带入ASME B31G-1991和ASME B31G-2009标准的计算方法中，得到新的计算方法ASME B31G-1991-2和ASME B31G-2009-2，具体计算结果如表3所示。

将表3中采用ASME B31G-1991、ASME B31G-2009、ASME B31G-1991-2和ASME B31G-2009-2方法计算的管道失效压力值与采用ANSYS非线性有限元法的预测值进行对比，得到残差平方和，如表3所示。可以看出，应用实际面积因子(ASME B31G-1991-2和ASME B31G-2009-2)计算的残差平方和小于应用等效面积因子(ASME B31G-1991和ASME B31G-2009)计算的残差平方和，尤其是采用ASME B31G-2009-2方法计算的残差平方和明显小于采用ASME B31G-2009方法计算的，表明实际面积因子对ASME B31G-1991和ASME B31G-2009计算结果的适应性有重大影响。

(a) 单层腐蚀 (b) 环向双层腐蚀

(c) 轴向双层腐蚀 (d) 轴向三层腐蚀 (e) 轴向四层腐蚀 图2 具有不同实际面积因子腐蚀的有限元模型Fig. 2 Different equivalent realistic area factor finite element models for corrosion: (a)single layer corrosion; (b)ring double layer corrosion; (c) axial double layer corrosion; (d)three layers of axial corrosion; (e) four layers of axial corrosion

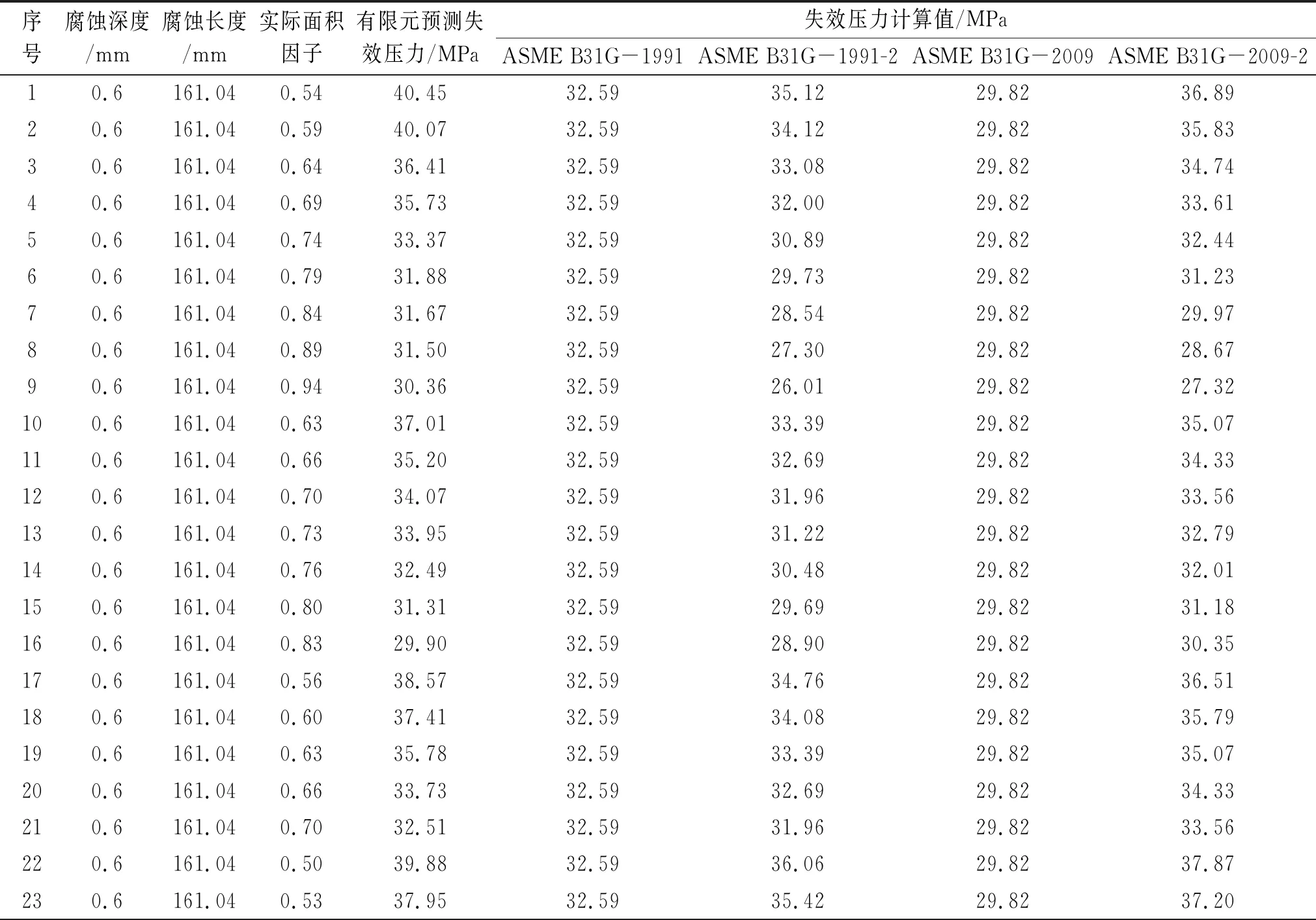
表3 管道失效压力的非线性有限元预测值与不同标准方法计算值Tab. 3 Pipeline failure pressure values predicted by nonlinear finite element method and calculated according to different standard methods

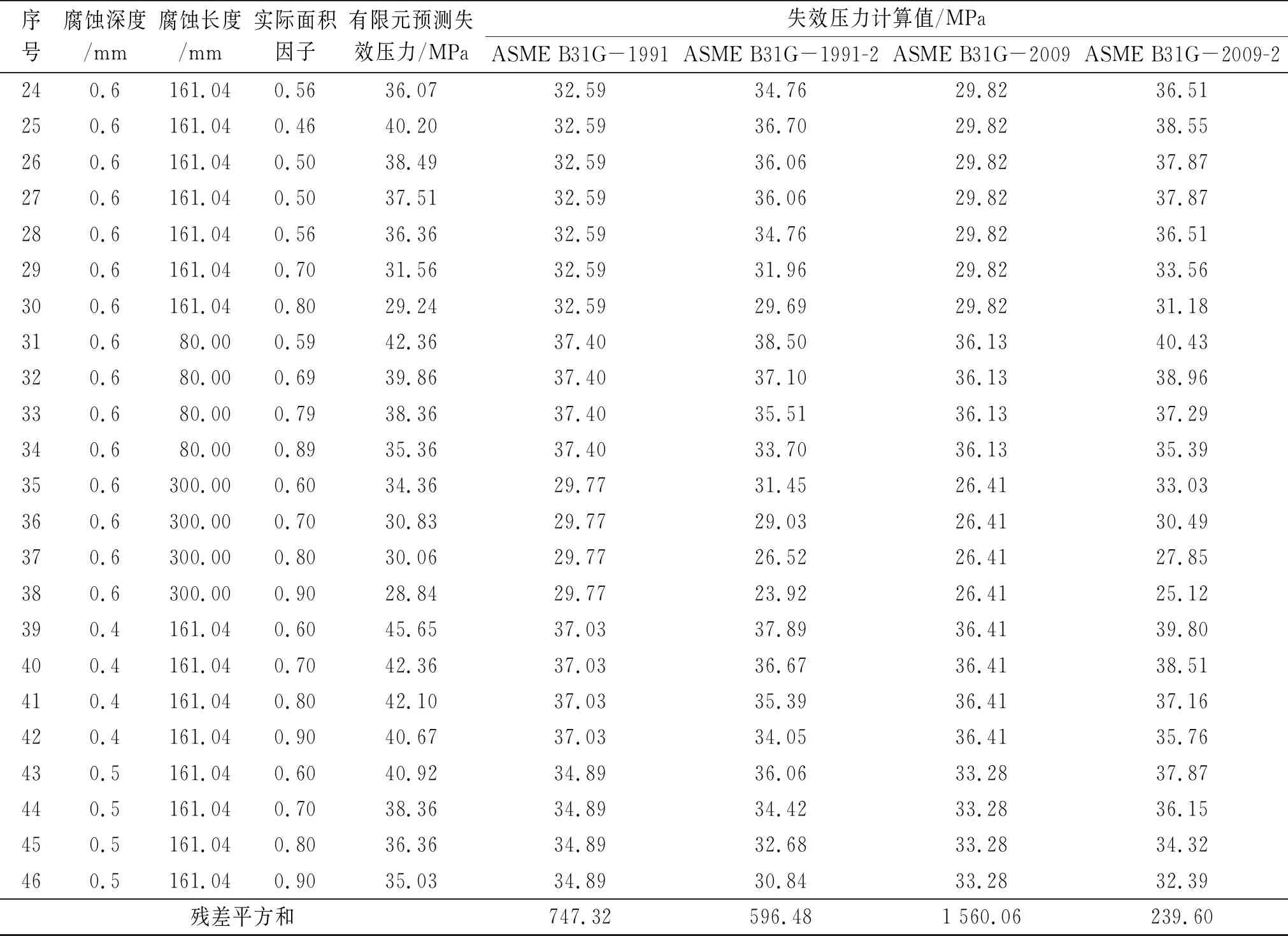
表3(续)

4种标准方法计算得到的误差分析如图3所示。可以看出，相比ASME B31G-1991和ASME B31G-2009，应用了实际面积因子的ASME B31G-1991-2和ASME B31G-2009-2方法的计算结果具有如下改观：(1) 误差分布平稳，采用ASME B31G-1991-2的46例计算结果中，计算误差分布在-1.5%～20%的范围内，大部分误差分布在10%左右，而采用ASME B31G方法的计算误差分布在-12%～20%范围内，且分布范围具有较大的跳跃性，结果不稳定；ASME B31G-2009-2与ASME B31G-2009标准方法具有同样的特点，而且ASME B31G-2009标准方法的计算结果跳跃性更大，稳定性较ASME B31G-1991方法的差；(2) 采用ASME B31G-1991方法计算的结果中,有超过12例出现了危险预测，即预测值大于实际失效压力，而采用ASME B31G-1991-2方法计算的仅有2例出现了危险预测，采用ASME B31G-2009-2方法计算的出现7例危险预测，但危险预测维持在5%的范围内。

2 新等效面积因子的影响

综合上文所述，依据有限的腐蚀缺陷信息，如腐蚀长度、腐蚀宽度、腐蚀深度等，准确描述实际面积因子，对提高ASME B31G系列评价方法的准确性、稳定性、安全性具有重要意义。因此以延长油田吴起采油厂油井采出液管线、注水管线以及外输油管线为研究对象，应用3D测试方法描述腐蚀形貌，计算腐蚀切向最大投影面积，得到实际面积因子，分析了近百处腐蚀，分析结果如表4所示，并提出新等效面积因子确定方法，用以描述实际面积因子。表4中腐蚀案例的管材信息如表5所示。

对表4中的74例腐蚀进行分析，发现管线腐蚀形貌与管线直径、壁厚关系不大，但与管线运行工况、输送介质、管材等条件有关，这涉及到管线的腐蚀机理，在此不作具体分析。管线腐蚀切向投影特点主要分成如图4所示的四类。

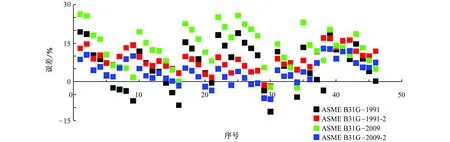
图3 应用实际面积因子的不同ASME B31G公式的误差分析Fig. 3 Error analysis of different ASME B31G formulas with real area factor

表4 腐蚀切向投影面积因子分析Tab. 4 Analysis of tangential projection area factors of corrosion

表4(续)

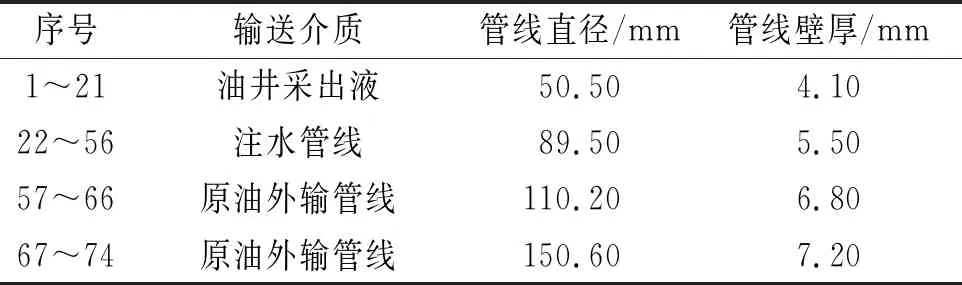
表5 表4中腐蚀案例的管线参数Tab. 5 Parameters of pipeline in corrosion cases inTable 4

第一类腐蚀切向投影形貌：局部腐蚀，腐蚀深度较浅，一般小于1.5 mm，腐蚀外围轮廓呈圆形或者椭圆形，直径一般小于15 mm，此类占大部分，表中并未全部统计，本文案例约有7例，如图4(a)所示，这类实际面积因子取值在0.60～0.75。

第二类腐蚀切向投影形貌：局部腐蚀，腐蚀深度较深，一般大于1.5 mm，腐蚀外围轮廓呈圆形或者椭圆形，直径一般小于15 mm，甚至10 mm，这类较第一类少很多。这类是油气集输管线失效的主要原因，是本研究的重点，共列举了约28例。这类是在第一类局部腐蚀的基础上发展起来的，第一类局部腐蚀内部环境与腐蚀介质之间的物质交换较管内其他位置缓慢，长时间累积就会诱发闭塞电池自催化效应[13]，发生氧浓差电化学腐蚀，局部腐蚀内部形成如图4(b)所示的水滴形局部腐蚀，这类实际面积因子取值在0.75～0.85。

第三类腐蚀切向投影形貌：均匀腐蚀，腐蚀深度较浅，一般不会超过1.5 mm，具有一定的腐蚀宽度，腐蚀长度超过20 mm，腐蚀长度/宽度一般大于2，腐蚀外围轮廓一般呈矩形。这类腐蚀较多，案例约有22例，ASME B31G-1984以及修正版的B31G的评价对象主要针对这类腐蚀，如图4(c)所示，因这类均匀腐蚀底部平整，均匀腐蚀区域内不存在局部腐蚀，实际面积因子取值接近最大腐蚀深度与腐蚀长度形成的矩形面积，在0.85～0.95。

第四类腐蚀切向投影形貌：均匀腐蚀与局部腐蚀的结合类型，如图4(d)所示，其与第三类腐蚀的区别主要是在均匀腐蚀区域存在局部腐蚀，均匀腐蚀区域深度与第三类类似，一般不超过1.5 mm，而均匀腐蚀区域的局部腐蚀深度较深，整体一般超过2 mm(包括均匀腐蚀区域的深度)，针对这类腐蚀，漏磁检测给出的腐蚀长度、宽度为均匀腐蚀的长度、宽度，而腐蚀深度为局部腐蚀深度，因此这类实际面积因子通常都小于0.5，取值范围一般在0.2～0.5，因均匀腐蚀区域腐蚀深度一般小于1.5 mm，大部分小于1.2 mm，因此，第四种腐蚀切向投影面积因子的取值与区域内局部腐蚀的深度直接相关，深度越大，实际面积因子则越小。

上述分析知道，可依据如下方法判断腐蚀类型，并依据腐蚀类型确定等效面积因子的取值范围。

第一类腐蚀的确认方法：先分析腐蚀深度，如果深度小于1.5 mm，则腐蚀属于第一、三类的可能性较大；再分析腐蚀长度，如果长度小于20 mm，则腐蚀属于第一类的可能性更大；最后再看腐蚀长度与腐蚀宽度比，如果比值小于2，则认为属于第一类。

第二类腐蚀的确认方法：先分析腐蚀深度，如果深度大于1.5 mm，则腐蚀属于第二、四类的可能性较大；再分析腐蚀长度，如果长度小于20 mm，则腐蚀属于第二类的可能性更大；最后再看腐蚀长度与腐蚀宽度比，如果比值小于2，则认为属于第二类腐蚀。

第三类腐蚀的确认方法：先分析腐蚀深度，如果深度小于1.5 mm，则腐蚀属于第一、第三类的可能性较大；再分析腐蚀长度，如果长度大于20 mm，则腐蚀属于第三类的可能性更大；最后再看腐蚀长度与腐蚀宽度比，如果比值大于2，则认为属于第三类腐蚀。

第四类腐蚀的确认方法：先分析腐蚀深度，如果深度大于1.5 mm，则腐蚀属于第二、第四类的可能性较大；再分析腐蚀长度，如果长度大于20 mm，则腐蚀属于第四类的可能性更大；最后再看腐蚀长度与腐蚀宽度比，如果比值大于2，则认为属于第四类腐蚀。

通过明确腐蚀类别的方法可以大致确定新等效面积因子s′的取值范围，但腐蚀形貌特征参数，如腐蚀深度1.5 mm、腐蚀长度20 mm等的选择会导致四类腐蚀之间存在较大的交集，因此，为了更准确地描述新等效面积因子的取值，需要可靠性更高的腐蚀形貌特点。

(a) 第一种 (b) 第二种 (c) 第三种 (d) 第四种 图4 四种典型的腐蚀缺陷切向投影形貌Fig. 4 Four types of typical corrosion tangential projection topography: (a) type one; (b) type two; (c) type three; (d) type four

图5表示腐蚀深度对新等效面积因子的影响。从图5可以看出，当腐蚀深度大于临界值3.5 mm后，新等效面积因子的取值只有2个范围区间，即第二、第四类腐蚀新等效面积因子的取值区间;当腐蚀深度范围在1.5～3.5 mm时，新等效面积因子的取值区间为0.35～0.95，其范围非常宽泛，不易确定。

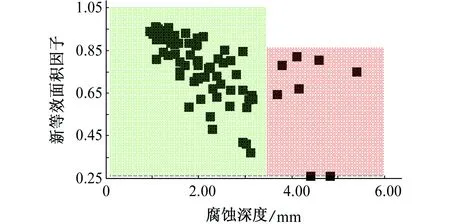
图5 腐蚀深度对新等效面积因子的影响Fig. 5 Effect of corrosion depth on the new equivalent area factor

图6表示腐蚀长度对新等效面积因子的影响。从图6可以看出，当腐蚀长度大于临界值40 mm后，新等效面积因子的取值只有2个范围区间，即第三、第四类腐蚀新等效面积因子的取值区间;当腐蚀长度范围在20～40 mm时，新等效面积因子的取值区间为0.5～0.95，其范围非常宽泛，不易确定。

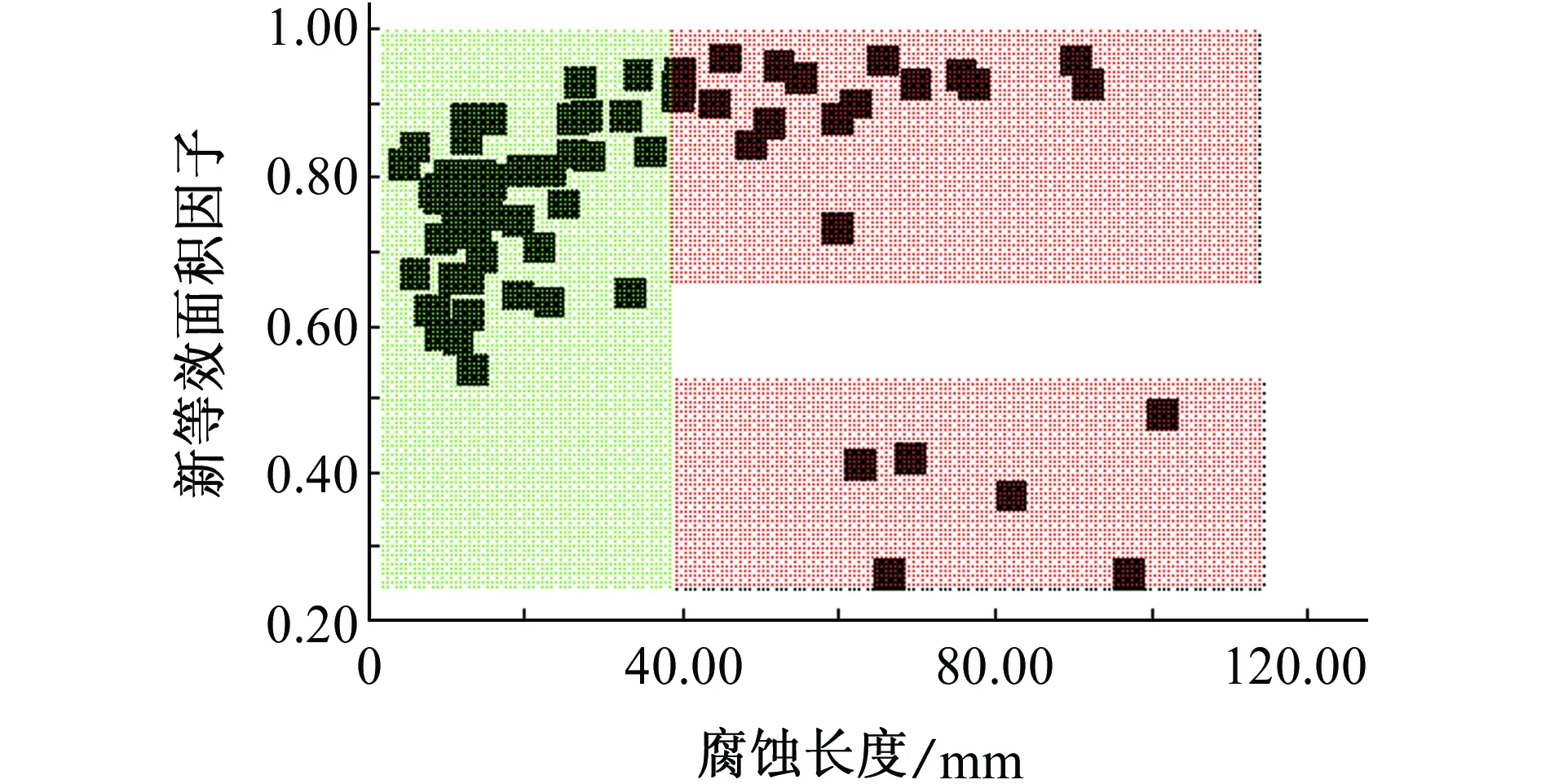
图6 腐蚀长度对新等效面积因子的影响Fig. 6 Effect of corrosion length on the new equivalent area factor

3 实例分析

用新等效面积因子代替等效面积因子带入ASME B31G-1991、ASME B31G-2009方法中，得到新计算方法ASME B31G-1991-3、ASME B31G-2009-3。选取文献[14-19]中X42、X46、X52三种不同钢级12例含轴向腐蚀管道的爆破失效压力，分析ASME B31G-1991-3、ASME B31G-2009-3计算结果的适应性，结果如表6所示。从表6可以看出，ASME B31G-1991-3计算得到的失效压力与爆破试验值之间的残差平方和是用ASME B31G-1991方法计算的1/2，ASME B31G-2009-3计算得到的失效压力与爆破试验值之间的残差平方和是ASME B31G-2009计算的2/7。这表明新描述方法得到的新等效面积因子的取值优于ASME B31G-1991和ASME B31G-2009方法的选值。

4种方法计算得到的误差分析如图7所示。可以看出，相比ASME B31G-1991和ASME B31G-2009方法，应用了新等效面积因子的ASME B31G-1991-3和ASME B31G-2009-3方法与图3所示的误差分析类似，都具有误差分布平稳的特点，ASME B31G-1991-3的计算误差分布在20%以内，平均约为10%，而ASME B31G-1991的计算误差分布在50%以内，且分布范围具有较大的跳跃性，结果不稳定；ASME B31G-2009-3方法得到的误差分析具有同样的特点。

4 结论

(1) 面积因子对ASME B31G-1991和ASME B31G-2009方法的计算结果具有重要影响，应用了实际面积因子的ASME B31G-1991和ASME B31G-2009方法计算结果与非线性有限元预测结果的残差平方和小，误差分布平稳，大部分计算结果分布在10%左右；危险预测出现频率低，且危险预测一般维持在5%的范围内。

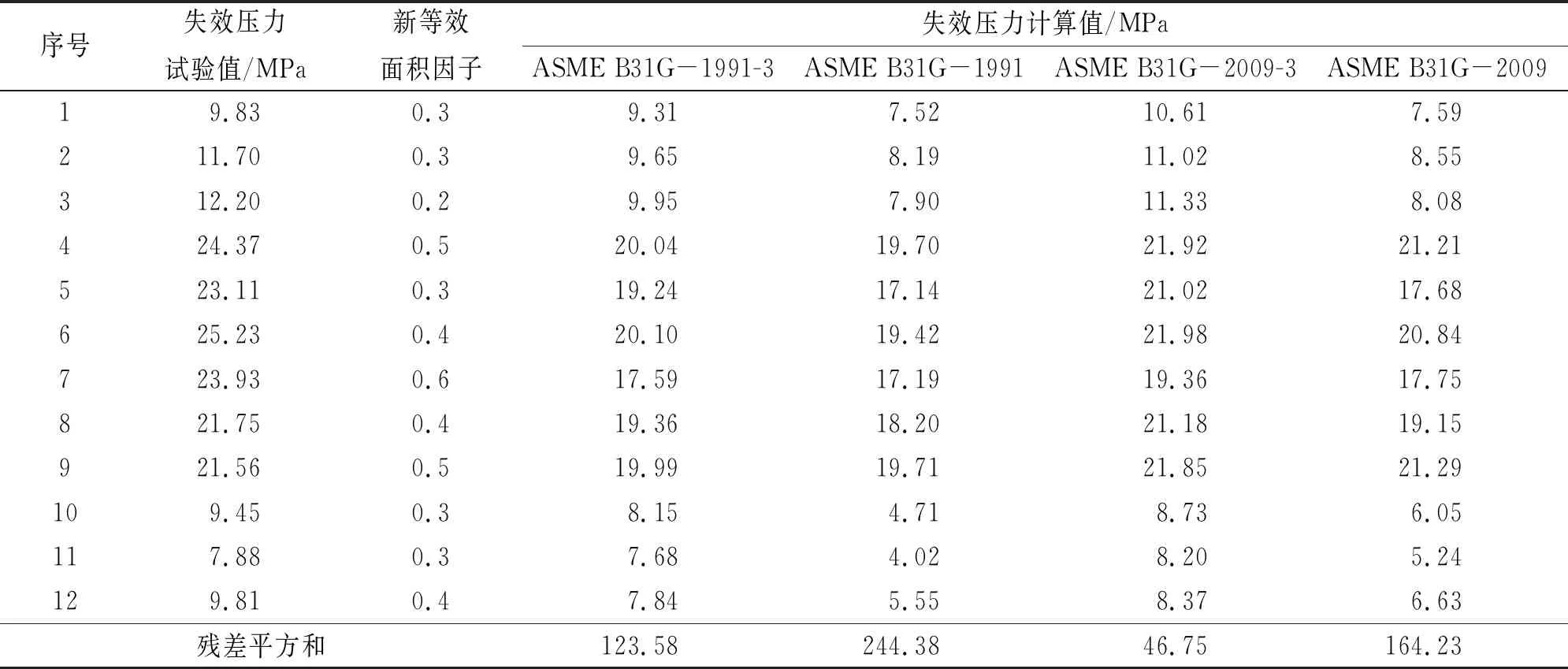
表6 管道失效压力的试验值与不同标准方法的计算值Tab. 6 Test values and calculated values according to different standard methods for pipeline failure pressure

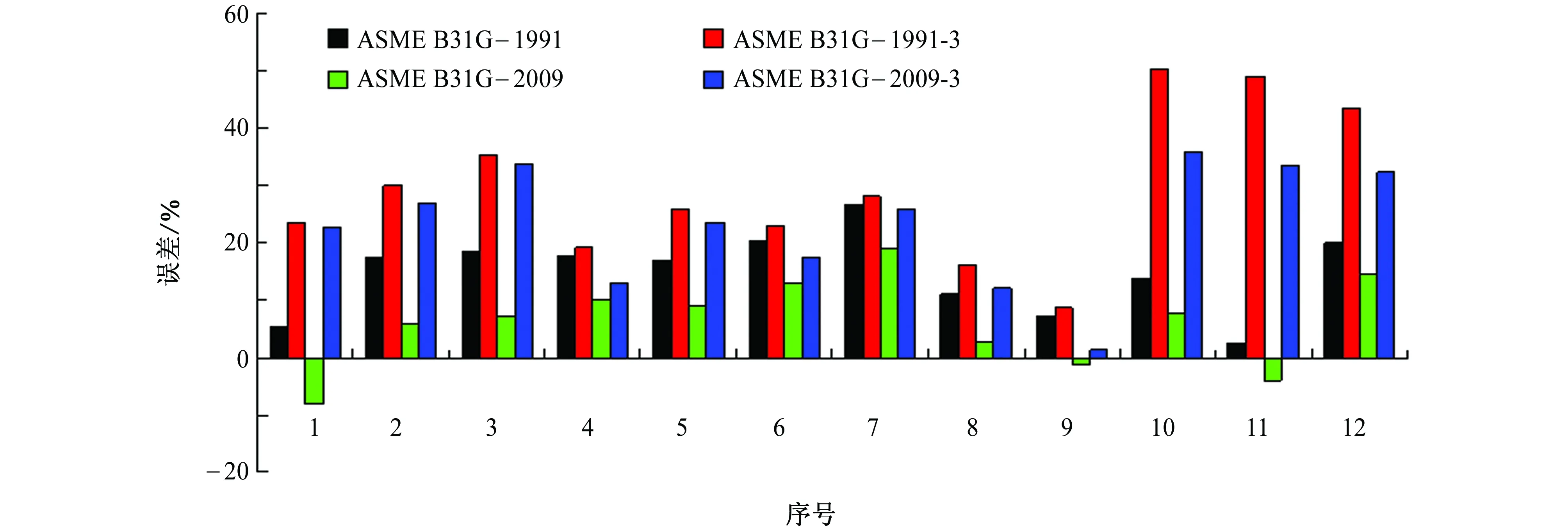
图7 应用新等效面积因子的不同ASME B31G公式的误差分析Fig. 7 Error analysis of different ASME B31G formulas with the new equivalent area factor

(2) 针对腐蚀深度、长度以及宽度特点，提出了四种腐蚀形貌类型及其划分方法，描述了四种腐蚀类型的深度、长度、腐蚀形态特点，并依据统计结果提出了各类面积因子的取值范围及计算方法。

(3) 为了更精确地描述等效面积因子的取值，给出了结合腐蚀深度临界值3.5 mm、腐蚀长度临界值40 mm以及四种腐蚀形貌类型特点三个方面的信息优化等效面积因子的取值方法。

(4) 应用新等效面积因子的ASME B31G-1991和ASME B31G-2009方法的计算结果与已有的爆破试验数据对比，残差平方和以及误差分布的稳定性明显优于应用固定等效面积因子。