水文计算中Γ函数及Excel算法

2

(1.云南水利水电职业学院，昆明 650499；2.昆明理工大学 建筑工程学院，昆明 650500)

Γ函数作为一种超越函数，在工程水文学中有着重要应用，水文频率计算和流域汇流计算中的P-Ⅲ型分布的概率密度函数和瞬时单位线都是用Γ函数来表示的。求解以上问题时，需要求解Γ函数，多年来不同学者应用不同的手段进行求解，但始终没有一种简单易行的方法；传统的计算方法需要查相关表格进行手工计算，但只能查到离散的数值，其他数值需要插值计算，这样不仅增加了插值误差，且计算量大，效率低下。Excel作为一款现代办公运用广泛的软件，在数据处理、分析计算和绘图方面都有着强大的功能,在水文计算中运用Excel能方便快捷地解决相关问题。

1 Γ函数及Γ分布

Γ函数是用积分形式定义的超越函数，也叫欧拉第二积分，其表达式：

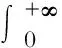
(1)

Γ分布是一种重要连续概率函数，其所包含的曲线形式较多、运用广泛，常用于可靠性理论和数理统计学中，“指数分布”和“χ2分布”都是Γ分布的特例[1]。其概率密度函数用Γ函数表示为：

(2)

式中，α为形状参数，β为尺度参数，x是随机变量。

2 Excel中GAMMA功能函数介绍

2.1 GAMMADIST函数的语法和用法

GAMMADIST函数的主要作用是返回Γ分布。可以使用此函数来研究具有偏态分布的变量。

函数语法:

GAMMADIST(x,α,β,cumulative)

用法说明：

x：计算Γ分布的数值;

α：形状参数;

β：尺度参数。当β=1.0，函数GAMMADIST返回标准Γ分布。

Cumulative：为逻辑值，决定函数的形式。如果cumulative为TRUE，函数GAMMADIST返回累积分布函数；如果为FALSE，则返回概率密度函数。

2.2 GAMMAINV函数的语法和用法

GAMMAINV函数的主要作用是返回Γ累积分布函数的反函数。

函数语法:

If P=GAMMADIST(x,α,β,TRUE),then GAMMAINV(P,α,β)=x

用法说明：

P：小于或等于变量x的Γ分布概率值;

α：形状参数;

β：尺度参数。当 当β=1.0，函数 GAMMADINV返回标准Γ分布;

x：相应概率P所对应的变量值。

给定一个Γ累积分布函数概率值P,应用GAMMAINV函数可计算出P=GAMMADIST(x,α,β,)中变量值x。但是GAMMAINV函数的计算精度取决于GAMMADIST的精度，GAMMAINV函数计算基于迭代搜索技术，如果搜索达100次还未收敛，则函数值返回错误值。

3 水文计算中的Γ函数

3.1 P-Ⅲ型频率曲线

P-Ⅲ型分布是我国在水文频率计算中常用的方法。P-Ⅲ型曲线是一条一端有限一端无限的不对称单峰曲线[3]，其概率密度函数为：

(3)

式中，形状参数α,尺度参数β和位置参数α0。

水文频率计算，需求出指定频率P所对应的随机变量xp的值，即需对概率密度函数进行积分，则有：

(4)

计算时，直接对(4)式进行积分非常困难，通常的做法是通过标准变换：

(5)

将(4)式标准化为：

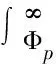
(6)

由此，把xp↔P的对应关系，转换为Φp↔P的对应关系，求出指定P值对应的Φp值，再通过(5)式即可得到xp↔P的对应关系，即得到所求的频率曲线。即使是标准变换后得到的(6)式积分仍无简易方法，通常是拟定Cs值,查Φ值表得出不同P对应Φp的值，但查表计算效率低，已不能适应现代电子化的工作环境。

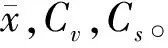
3.1.1Φp值的计算

通过进行中间变量t变换，对P-Ⅲ型分布进行标准化处理，使(4)式变为标准Γ分布，其对应的尺度参数：β=1.0。

令t=β(x-α0)，有：

(7)

(8)

此时，运用Excel中GAMMAINV函数，由(7)(8)式，有

(9)

(10)

3.1.2优选统计参数

运用P-Ⅲ型分布时，通常用样本矩估计总体，计算中的三个统计参数：

(11)

(12)

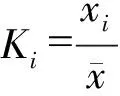
(13)

一般由式(13)计算所得的Cs值误差较大，需要调整，使所求频率曲线能较好地拟合样本数据。根据最小二乘法原理，运用Excel软件中线性回归函数INTERCEPT、SLOPE，按以下步骤优选参数：

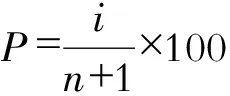
2)将Pi，Cs带入式(10)计算出率Φpi值，再通过式(5)即可计算出对应的xpi。

3)按Cs=nCv关系调整Cs(根据我国绝大部分河流统Cs/Cv值在2～3倍的范围，适当放大取值范围，n可取1.8～3.5)，替换第二步中的Cs值，计算出多组不同的Cs取值所对应的xpi。

4)根据最小二乘法原理，查找满足目标函数∑(xi-xpi)2=min的Cs即为最优。

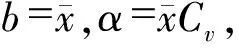
3.1.3偏态系数Cs的不同情况说明

1)一般当Cs>0时，按上述方法计算；

2)绘制海森概率格纸时，即Cs=0时，改用标准正态分布计算；

3)当拟合枯季流量或水位时常为负偏的序列，即Cs<0时，根据Γ函数性质，导出Φ＇p(Cs,P)=-ΦP(-Cs,1-P)。

3.2 瞬时单位线

在区域洪水预报中，所采用的瞬时单位线法是纳西于1957年提出，用一个不完全Γ分布函数表示一个单位地面净雨在流域出口断面形成的地面径流过程线。其表达式为

(14)

式中，n——流域调蓄能力的参数，相当于线性水库的个数;

K——线性水库蓄泄系数，相当于流域汇流时间的参数。

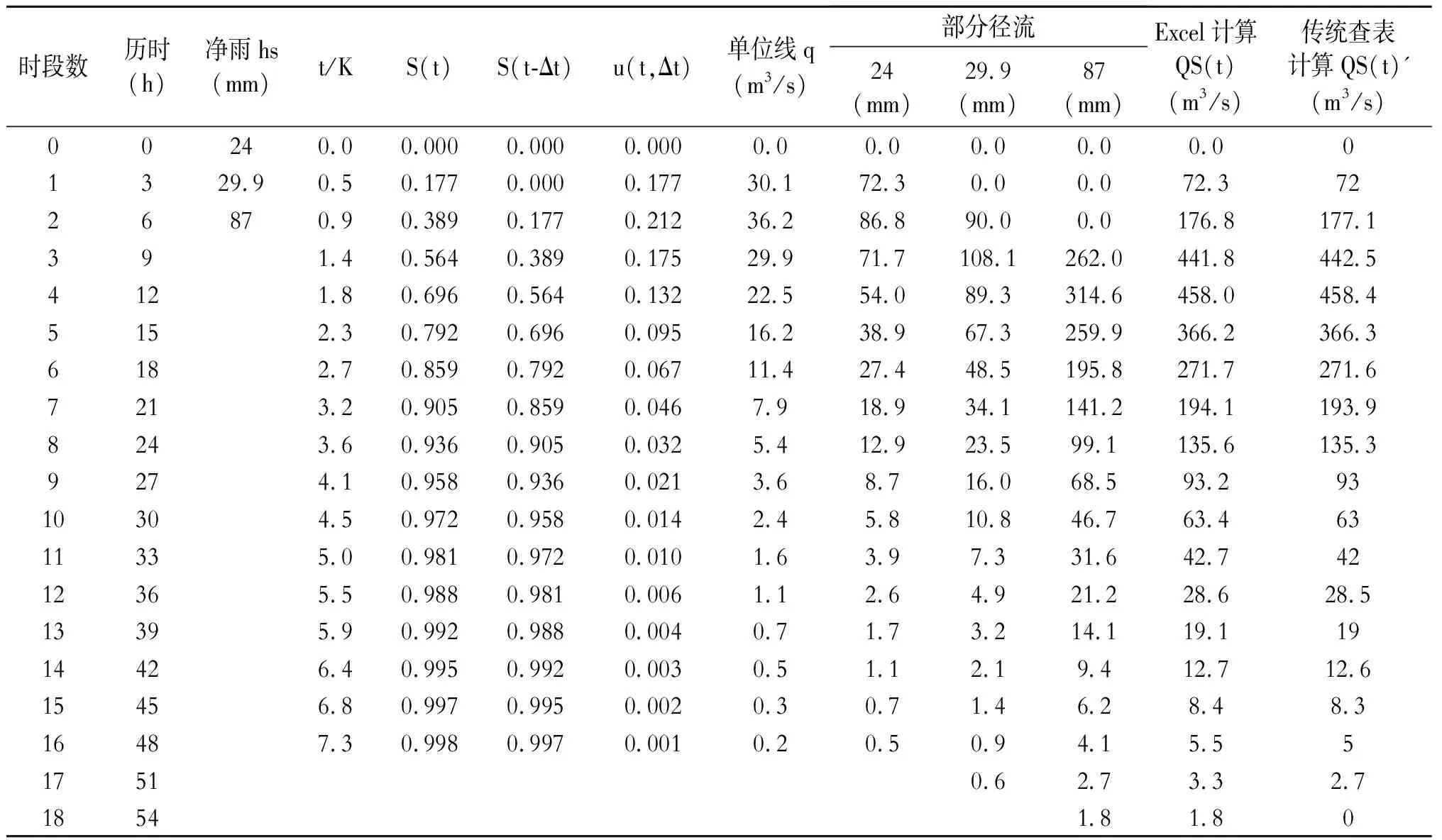
表1 地面洪水过程计算

实际的汇流计算中，通过将瞬时单位线转换为瞬时单位线的积分曲线，其表达式为：

(15)

故△t时段内单位线可表示为：

u(Δt,t)=S(t)-S(t-Δt)

(16)

流域面积F在时段Δt内，净雨深为10mm的时段单位线即可表示为：

(17)

最后再叠加各时段净雨对应的径流过程，得地面洪水过程,即有：

(18)

式中，m——地面净雨hsi的时段数

上述汇流计算中，S(t)曲线的求解，通常是查已制成的S(t)关系表。但同样运用Excel软件中Γ偏态分布的GAMMADIST函数即可快速求解S(t)曲线,且能有效避免由于中间参数t/K增加的舍入误差。故此，只需把GAMMADIST(x,α,β,cumulative)函数中参数x,α,β替换为数t/K，n，K,cumulative为TRUE，即可得瞬时单位线的积分曲线S(t)，由此，按式(16)(17)(18)即可进行汇流计算。

4 算 例

以文献[4]中例(5-2)为例。某流域面积F=184km2，流域调蓄能力参数n=1.5,线性水库蓄泄系数K=6.6h，时段△t=3h，用Excel计算地面洪水过程及结果如表1所示。

5 结 语

(1)通过Excel软件能够高效地求解水文频率计算和汇流计算中的Γ函数，改善了传统手工查表的繁琐计算工作，减小了计算过程中的舍入误差，使计算结果更加精确，更加适宜现代电子办公化发展的需求。

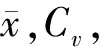
(3)讨论了频率计算中偏态系数Cs特殊取值时的计算方法。