基于ANSYS 模拟的管道堵塞预测分析

邱春斌 孙向东 冷绪林 王国锋

1中国石油天然气股份公司西气东输管道分公司

2杭州和利时自动化有限公司

3中国石油管道局工程有限公司设计分公司

4中国石油集团渤海钻探工程有限公司定向井技术服务分公司

由于受管道变形或腐蚀、输送介质物理特性、外界环境条件、清管器堵塞等因素的影响，输送管道内容易形成堵塞[1]。若不能及时处理，堵塞情况会持续恶化，管道内压力急剧上升，引发管道泄漏或爆管等问题，造成巨大经济损失[2]。目前，用于检测管道堵塞的方法主要包括：超声波法、负压波法、频率响应法、仪器探测法和γ射线法等，这些方法需开挖管道、配套相应测量仪器、多次重复测试管道堵塞情况，操作量大、费用高，且排堵时间长，严重影响管道输送任务的完成。基于此，本文对输送管道堵塞进行系统实验设计，运用ANSYS仿真软件模拟分析不同堵塞情况下对输水管道沿线特别是靠近堵塞部分的管内压力的影响，提供一种依据管道起始点间压降定量预测堵塞的方法，并通过实验验证该方法的实用性与准确性，为改进和简化管道堵塞问题提供必要的理论支持。

1 仿真模拟

1.1 模型建立

通过ANSYS 软件建立三维管道模型，图1a 为正常输送水平管道模型，图1b 为管道堵塞模型，为了降低模拟计算的复杂度，可将堵塞管段的边界规则化处理，将其等效视为变径管道。输送管道的堵塞情况可用堵塞位置、堵塞强度和堵塞长度表示。堵塞位置即堵塞段起点到管道入口的距离；堵塞长度即模型中变径管的长度；堵塞强度为堵塞面积占管道流通面积的百分比。因此，通过调整变径管段的位置、长度及内径，来模拟输送管道不同堵塞位置、堵塞长度和堵塞强度。考虑到仿真结果与实验结果的对照性，用于仿真的管道模型长2 m，管道内径为20 mm，管内介质为水相，模型中所涉及的具体管道参数见表1。

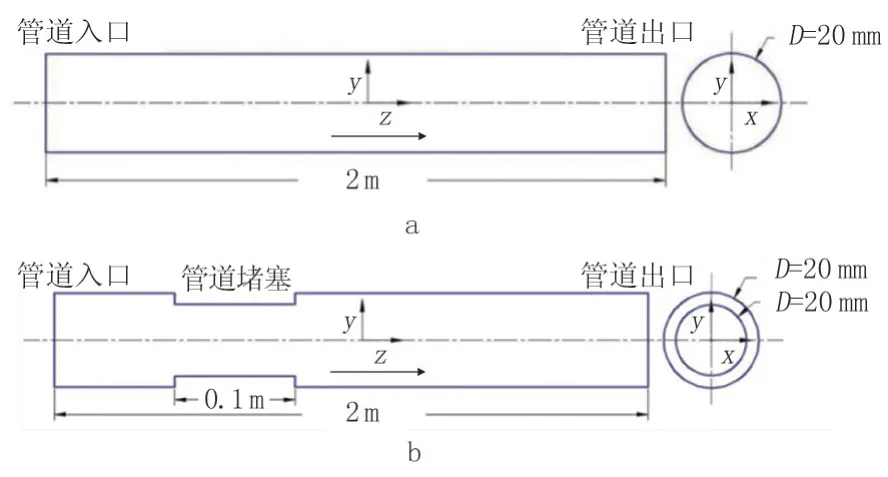
图1 输送管道ANSYS 仿真模型示意图Fig.1 ANSYS simulation model schematic diagram of transportation pipeline

表1 CFD 计算模型参数Tab.1 Parameters of CFD computational model

采用ANSYS 中的MODELER 和MESH 模块对管道模型进行模型建立和网格划分。采用四面体网格划分方法，将管道堵塞模型划分成350 000 个网格。一般采用偏度作为评价网格划分优劣的评价指标，偏度值低于0.8 即可评为优质网格[3-4]。截取输送管道的偏度截面图（图2），可以看出偏度值大多低于0.22，因此，可以判定该堵塞模型可以用于管道堵塞模拟计算。

1.2 模拟内容及方案

利用所建的三维管网模型模拟并分析稳态情况下输送管道前后的沿线压力、压力梯度变化趋势，选取平行于管道轴线且处于不同径向位置的压力及压力梯度值，绘制沿线压力与压力梯度的变化曲线。主要工况包括输送管道正常运行模拟、出现管道堵塞后的压力变化模拟，以及不同堵塞情况对沿线压力及管道起始点间压降的影响模拟。根据所模拟的研究内容，选择合理的运行参数作为管道模型的边界条件，然后进行模拟分析，共设计11 组模拟方案对处于正常运行和含堵塞运行的管道进行模拟，具体模拟方案如表2 所示。

图2 三维管网模型网格图Fig.2 Gird chart of 3D pipeline network model

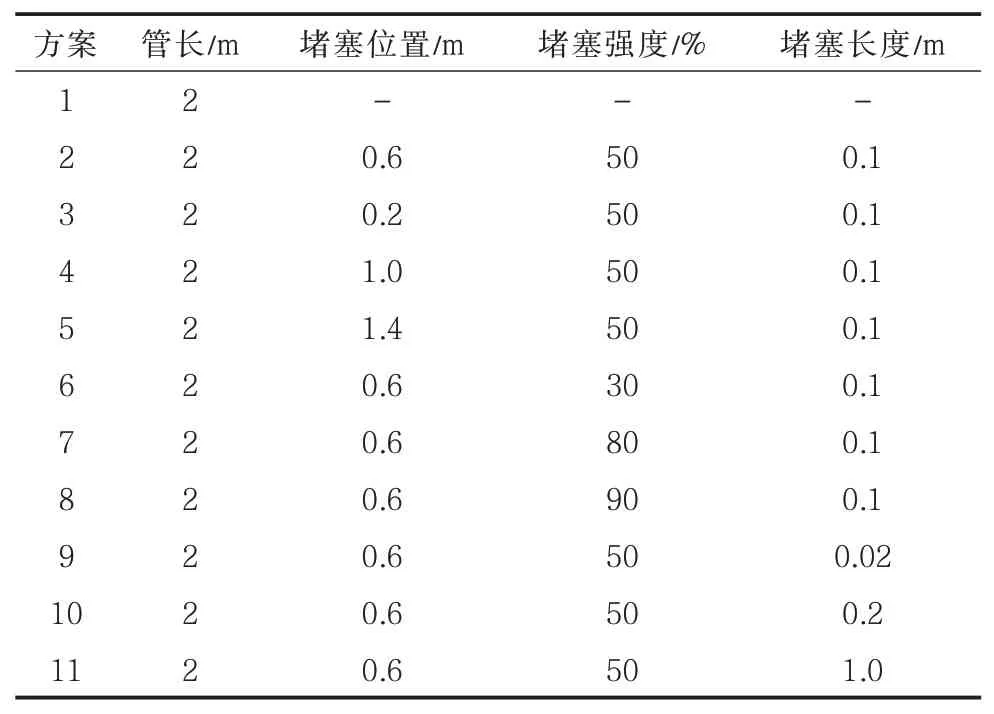
表2 输送管道仿真模拟方案Tab.2 Simulation scheme of transportation pipeline

2 堵塞对管内压力分布的影响

2.1 正常运行

运行表2 中的方案1，即由ANSYS 建立的无堵塞输送模型，管道沿线压力、压力梯度经过多次试算，即可以达到稳定运行状态（图3）。分析可知，该输送管道稳定运行，沿线压力呈递减趋势且缓慢下降，压力梯度分布是一条变化不明显的直线，其因管道起终点间摩阻损失较小所致。经过数值拟合，该管道沿线压力分布的拟合关系式为：y=7.94x2-265.66x+14 298.89（确定系数R2=1）的二次函数，这与管道输送沿线实际压力变化一致[5]。

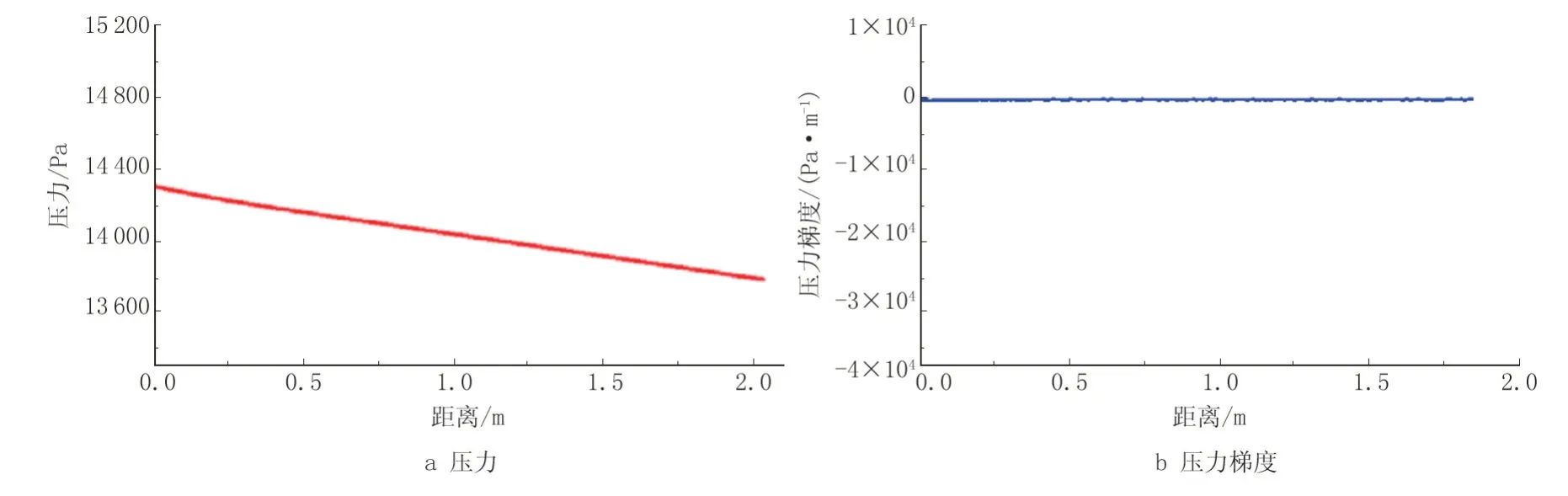
图3 输送管道正常运行时沿线压力、压力梯度变化曲线Fig.3 Variation curve of pressure and pressure gradient when the transportation pipeline operates normally

2.2 管道堵塞

运行表2 中的方案2，为对照方便，该管道堵塞模型设为标准模型（图1b），当管道达到稳定状态时即可得到管道堵塞后沿线压力变化曲线（图4）。取管道中心线和平行于中心线且低于堵塞边界1 mm、2 mm、5 mm 的平行线，导出相应压力梯度值绘制成沿线压力梯度变化曲线（图5）。由图4、图5 分析可知，输送管道发生堵塞后，由于运行面积减小，使得管道起终点间压降、压力梯度增大，且主要集中在堵塞管段，尤其越靠近堵塞边界，压力梯度变化幅度明显。因此，可以通过检测输送管道起始点间压降以及压力分布曲线的突变点来检验及定位堵塞情况。

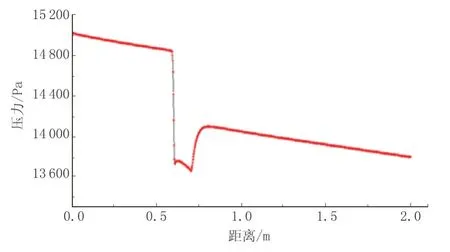
图4 输送管道堵塞运行时沿线压力变化曲线Fig.4 Variation curve of pressure when the transportation pipeline operstes with blockage

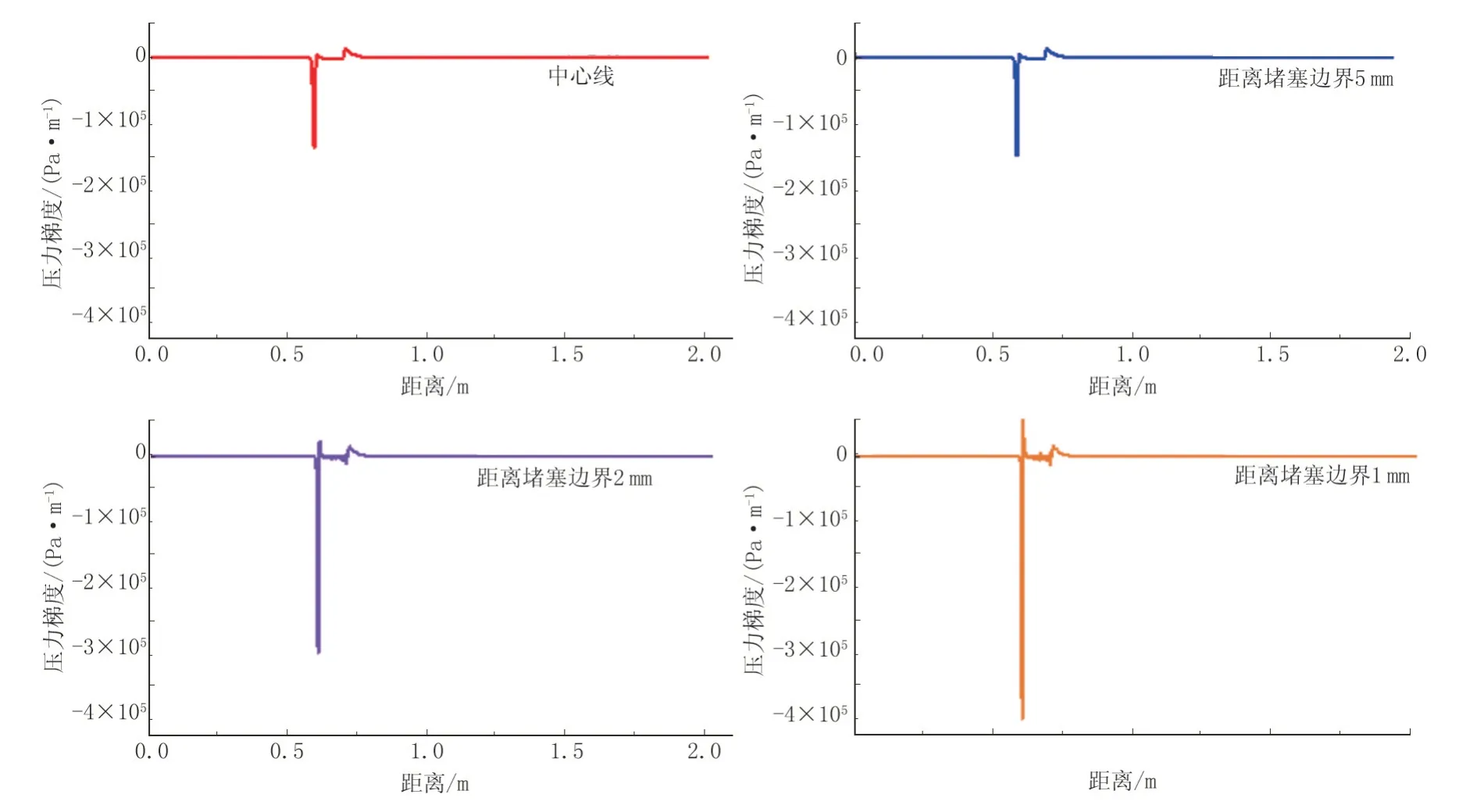
图5 输送管道堵塞运行时沿线压力梯度变化曲线Fig.5 Variation curve of pressure gradient when the transportation pileline operates with blockage

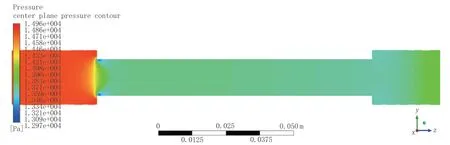
图6 输送管道堵塞运行时沿线压力分布曲线Fig.6 Pressure distribution curve when the transportation pileline operates with blockage

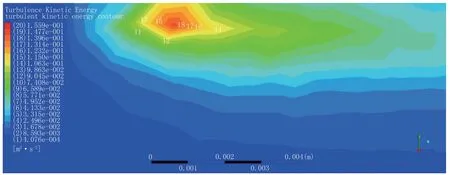
图7 输送管道堵塞运行时湍动能分布曲线Fig.7 Turbulence kinetic energy distribution curve when the transportation pileline operates with blockage

为更加直观对照管道堵塞位置的压力分布变化，取管道中心线所在轴面，导出该平面的压力平面图。如图6 所示，当管内流体流经堵塞位置时，压力变化明显，因管内流通面积减小导致管流流速剧增，迫使管内压力急剧降低；若管段堵塞距离较长，会进一步造成动力势能和压力势能的损耗，从而造成管输任务低效运行。同样，通过截取管道中心线轴面的湍动能分布曲线（图7），进一步验证管内流体流经堵塞位置时，湍动能因管流的剧烈激扰而增大，经粗算可知，湍动能差距可达400 倍，剧烈、长时间的堵塞状况，极易诱发管段腐蚀、断裂的情况发生。

2.3 不同堵塞位置

为对比分析堵塞位置对管道沿线压力、压力梯度的影响，另选取三组不同堵塞位置与标准模型进行对比模拟，具体参数见表2 中第3、4、5 组方案，堵塞位置为距离管道起点0.2 m、1.0 m、1.4 m。当管道模型达到稳定状态时，即可得到由不同堵塞位置引起的沿线压力、压力梯度变化曲线，如图8、图9 所示。分析可知，管道起终点压降主要集中在堵塞管段部分，因不同堵塞位置所导致的起终点压降之间的差异很小。管道沿线压力、压力梯度分布趋势基本相同，因此，不宜采用管道起终点压降值来预测分析堵塞位置。

图8 输送管道在不同堵塞位置运行时沿线压力变化曲线Fig.8 Variation curve of pressure when the transportation pipeline operates with blockage in various locations

2.4 不同堵塞强度

为对比分析堵塞强度对管道沿线压力、压力梯度的影响，另选取三组不同堵塞强度与标准模型进行对比模拟，具体参数见表2 中第6、7、8 组方案，堵塞强度设为30%、80%、90%。当管道模型达到稳定状态下，即可得到由不同堵塞强度引起的沿线压力、压力梯度变化曲线，如图10、图11 所示。分析可知，管道起终点间压降随堵塞强度的增大而显著增大，相应压力梯度呈现相同的变化趋势，压力和压力梯度的突变主要集中在堵塞入口与出口位置，尤其是当设定堵塞强度为90%时，最大压力梯度可达到-8.0×106Pa/m。

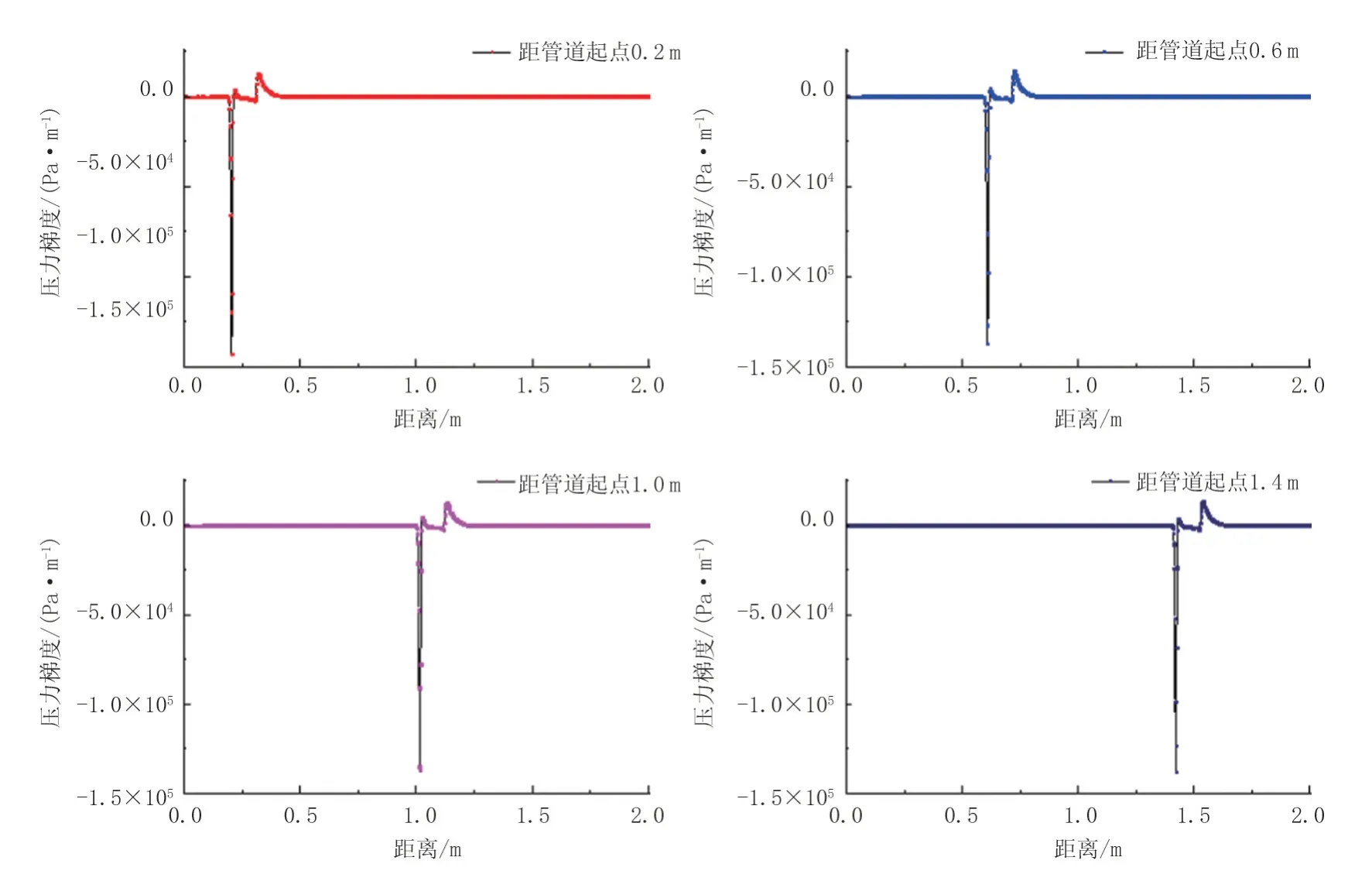
图9 输送管道在不同堵塞位置运行时沿线压力梯度变化曲线Fig.9 Pressure gradient variation curve when the transportation pileline operates with blockage in various locations

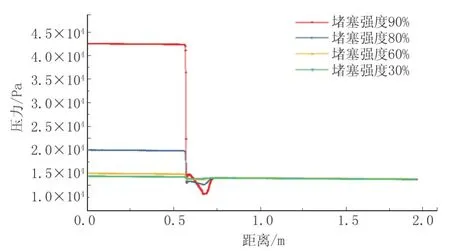
图10 输送管道在不同堵塞强度运行时沿线压力变化曲线Fig.10 Pressure variation curve when the transportation pipeline operates with different blockage strengths

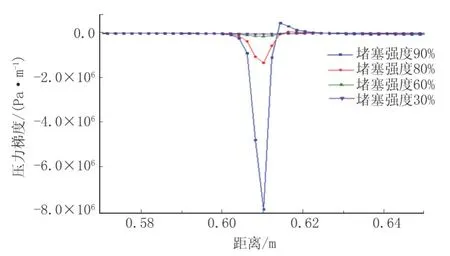
图11 输送管道在不同堵塞强度运行时沿线压力梯度变化曲线Fig.11 Pressure gradient variation curve when the transportation pipeline operates with different blockage strengths

2.5 不同堵塞长度

为对比分析堵塞长度对管道沿线压力、压力梯度的影响，另选取三组不同堵塞长度与标准模型进行对比模拟，具体参数见表2 中第9、10、11 组方案，堵塞长度设为0.02、0.20、1.0 m。当管道模型达到稳定状态时，即可得到由不同堵塞长度引起的沿线压力、压力梯度变化曲线，如图12、图13 所示。管道起终点间压降随堵塞长度的增大而逐渐增大，管道沿线压力在堵塞管段部分有明显变化。参照沿线压力梯度分布曲线可知，除堵塞部分压力梯度趋势一致外，堵塞部分压力梯度明显随堵塞长度增加而增大，尤其在堵塞部分起始点位置，压力梯度最大值可达到-1.4×105Pa/m。

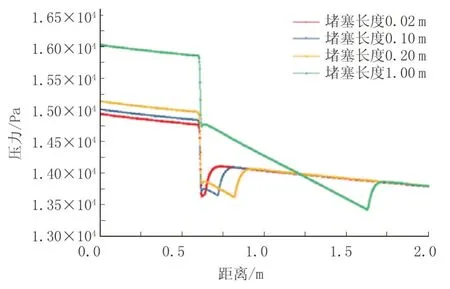
图12 输送管道在不同堵塞长度运行时沿线压力变化曲线Fig.12 Pressure variation curve when the transportation pipeline operates with different blockage lengths

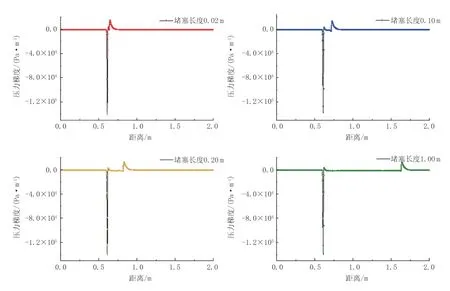
图13 输送管道在不同堵塞长度运行时沿线压力梯度变化曲线Fig.13 Pressure gradient variation curve when the transportation pipeline operates with different blockage lengths

2.6 堵塞预测模型

考虑到不同堵塞位置模拟结果对起始点间压降影响不明显，故本节对堵塞位置不做分析。依据不同堵塞强度和堵塞长度下管道起始点间压降变化规律，引入无量纲分析，将堵塞强度、堵塞长度及相应情况下管间压降转变为无量纲量，并绘制压降变化曲线，如图14 所示。

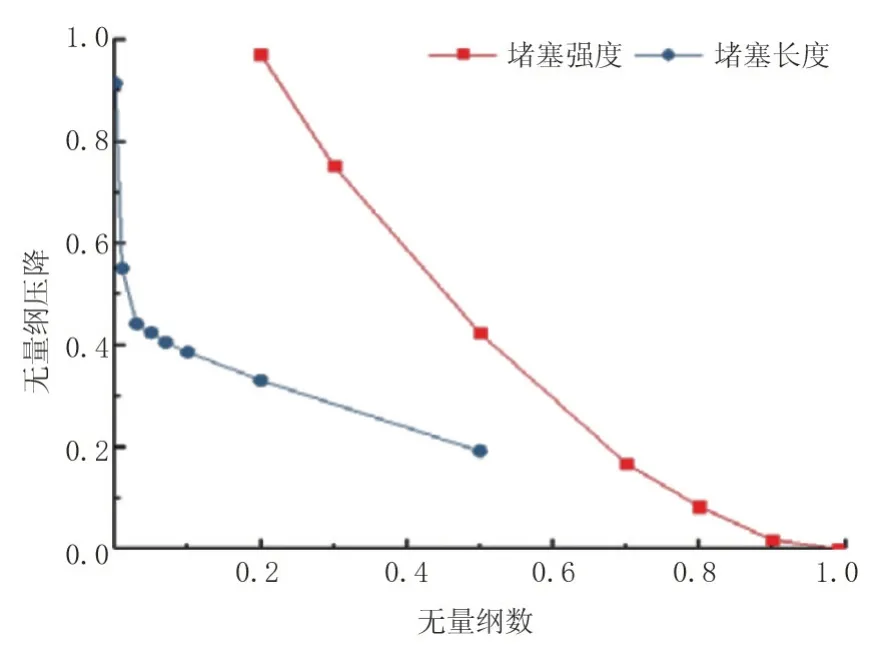
图14 输送管道在不同堵塞情况下沿线压降变化曲线Fig.14 Pressure drop variation curve of the transportation pipeline under different blockage conditions

依据曲线变化趋势对其进行拟合分析，可得到用于堵塞检测的预测模型，即

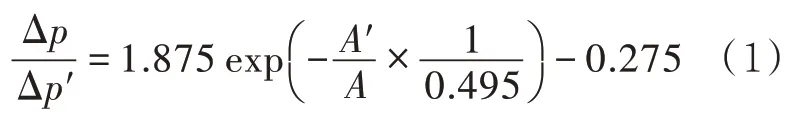
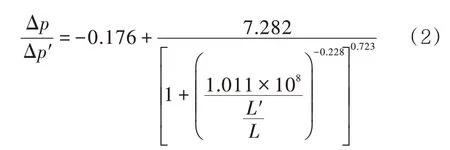
式中：Δp、Δp′为管道无堵塞和有堵塞情况下的起始点间压降，Pa；A、A′为管道无堵塞和有堵塞情况下的流通面积，mm2；L为管道流通长度，m；L′为管道有堵塞情况下的堵塞长度，m。

依据此预测模型，可利用管道起始点间压降来判断是否存在堵塞情况，若待检管道起始点间压降明显大于其正常运行时的压降，则可判断该管道存在堵塞情况。将管道运行数据输入预测模型，可求得关于堵塞强度和堵塞长度的唯一解，用于及时实施排堵措施。

3 实验验证

为验证文章中提出的输送管道堵塞预测模型，需进行相应堵塞实验，通过实验验证该方法的可操作性和实用性。

3.1 实验系统设计

实验系统由水箱、管道、计算机三部分组成，包括水泵、储水箱、流量计、堵塞管道、管道起始点间压力计、数据采集系统，图15 为输送管道堵塞实验系统。输水流量由流量计计量，从水泵排出的水经输送进入目标管道，通过目标管道起始点的压力计来计量压降变化，通过使用变径管来模拟目标管道的堵塞情况，不同堵塞情况下的压力变化由数据采集系统自动记录，并传输到计算机部分保存。

图15 输送管道堵塞实验系统Fig.15 Blockage experiment system of transportation pipeline

3.2 实验方案设计

由于不同堵塞情况的组合数量较大，不宜对全部组合进行评价，故针对单个堵塞案例，指定堵塞管段中心线与运行管道的中心线重合，在此基础上选取管道流通面积的50%、80%、90%作为不同的堵塞强度，选取堵塞长度为0.1 m、1.0 m、1.8 m。将上述数据组合可得到具体实验方案。

3.3 与堵塞预测结果对照分析

为了对比预测模型与实验结果的精确度，确定不同堵塞长度、堵塞强度对堵塞检测的影响，依据实验方案参数表中所列数据，代入到预测模型中，计算出预测管间压降与实验所得压降的误差情况。具体结果如表3 所示。

由表3 可知，实验管间压降与预测模型所计算的管间压降之间的误差不大，维持在10%左右，且预测模型对堵塞强度的检测精度略低于对堵塞长度的检测精确度，其中预测堵塞强度所得的管间压降均低于实验值，这是由于在实验管道堵塞部分流通面积的突变以及弯头阀门的存在，导致大量动势能损失，使得管间压降大于预测模型的计算值。

3.4 与Hysys 堵塞分析结果对照分析

为了进一步验证堵塞模型的准确性，建立输送管道Hysys 仿真模型（图16），由异径管段和管件接头构成管道堵塞模型。

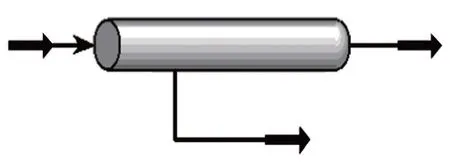
图16 输送管道Hysys 仿真模型示意图Fig.16 Hysys simulation model schematic diagram of transportation pipeline

经运行可得到管段的沿程压力分布情况，堵塞1 情况的Hysys 模拟结果如图17 所示。对比ANSYS堵塞模拟结果可知，管道内沿程压力变化趋势基本一致，管段堵塞造成管道沿程压降急剧降低；计算出预测管间压降与模拟实验所得压降的误差情况，具体结果如表4 所示，模拟管间压降与预测模型所计算的管间压降之间的误差低于20%，这与堵塞实验对照结果一致。

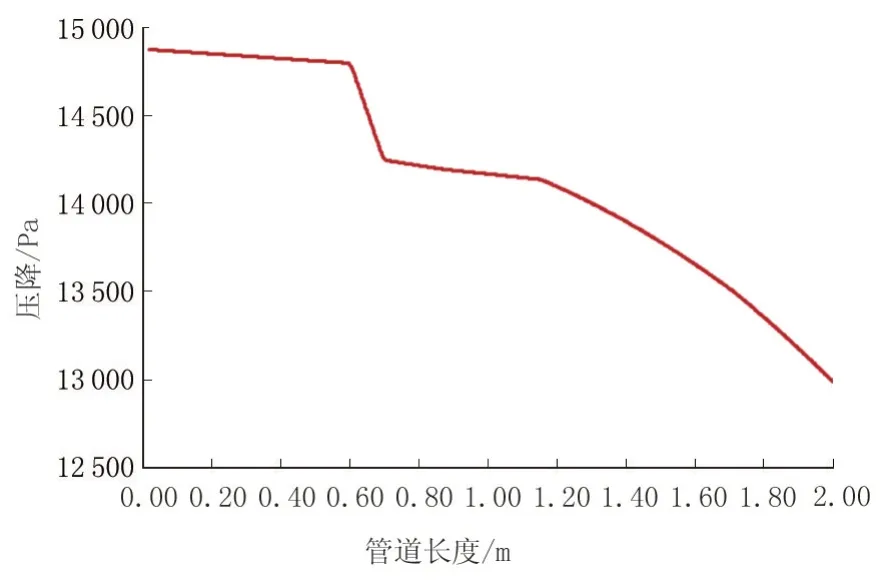
图17 Hysys 模拟输送管道堵塞运行时沿线压力变化曲线Fig.17 Pressare variation curve when the Hysys simulation transportation pipeline operates with blockage

表3 输送管道实验结果与预测结果对照Tab.3 Comparison between experimental and predicted results of transportation pipeline

表4 Hysys 模拟输送管道实验结果与预测结果对照Tab.4 Comparison between experimental and predicted results of Hysys simulation transportation pipeline

4 结论

基于ANSYS 仿真模拟，研究了在不同情况下管道堵塞对管道沿线压力、压力梯度的影响，基于无量纲分析提出了管道堵塞预测模型，并采用管道实验进一步验证了该模型对堵塞情况的预测精度和准确度，具体研究结论如下：

（1）当正常运行的管道在某处发生堵塞时，管道起终点间压降明显增大，且堵塞管段处的压力、压力梯度将发生突变，其余管段压力梯度与无堵塞管道压力梯度基本一致。

（2）对不同管道堵塞情况仿真模拟和分析结果表明：不同堵塞位置对管道起终点间压降影响不大，管线沿线压力、压力梯度变化趋势基本一致，主要变化集中在管段堵塞部分；随着堵塞强度逐渐增大，管道起始点间压降随之增大，相应压力梯度呈现相同的变化趋势；随着堵塞长度的逐渐增大，管道起始点间压降逐渐增大，堵塞部分压力梯度也随之增大。

（3）管道堵塞前后管间压降发生剧烈变化，可由此判断堵塞情况是否存在。依据无量纲分析方法提出了管道堵塞预测模型，并设计相应管道实验对其准确性进行验证，结果表明：预测模型结果与试验结果的误差维持在10%左右，且预测模型对堵塞长度的预测精度高于对堵塞强度的预测。