关于多角形数的余数的研究*
2019-12-24 03:04王明军
首都师范大学学报(自然科学版) 2019年6期
王 明 军
(渭南师范学院数理学院, 陕西 渭南 714000)
1 主要结论
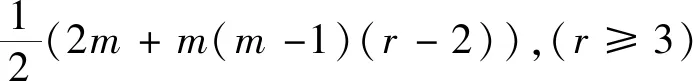
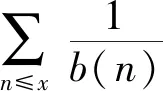
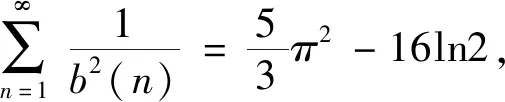
在文[5]中,作者定义了正整数的下部r角形数部分数列和上部r角形数部分数列,得到了两个精确的计算公式.
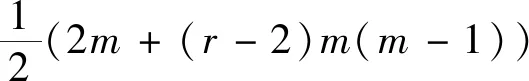
定理1对于任意实数x>1,a(n)表示正整数n的多角形数的余数,则有渐近公式
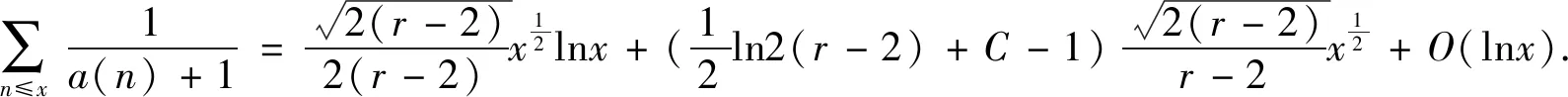
定理2对于任意实数x>1,σ(n)表示正整数n的约数之和,则有渐近公式
2 引 理
为了完成定理的证明,需要下面的引理.
引理1[7]对于任意的实数x≥1,有渐近公式
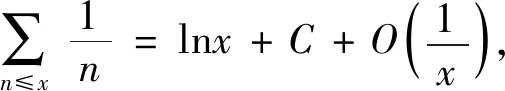
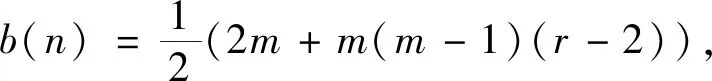
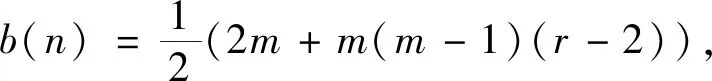
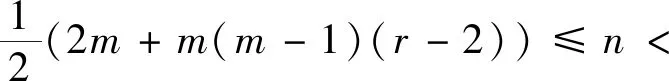
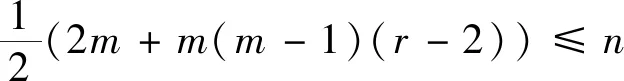
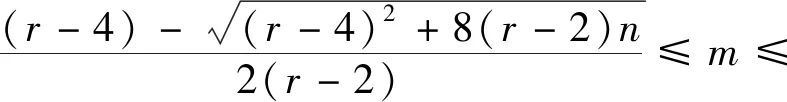
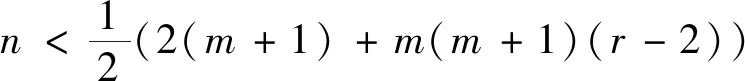
或者
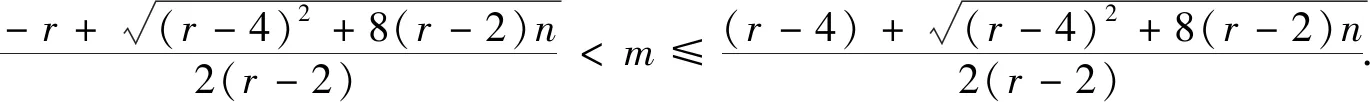
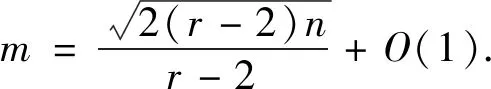
引理3[7]对所有的x≥1,有
3 定理的证明
3.1 定理1的证明
对于任意给定的正数x>1,设M是满足
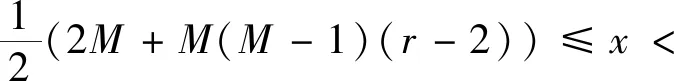
的正整数,由a(n)的定义及引理1有:
=lnM!+(ln(r-2)+C)M+O(lnM)
=MlnM+(ln(r-2)+C-1)M+O(lnM)
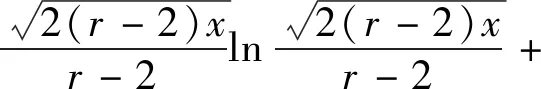
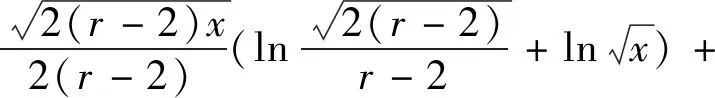
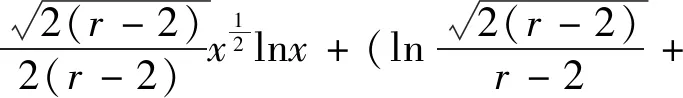
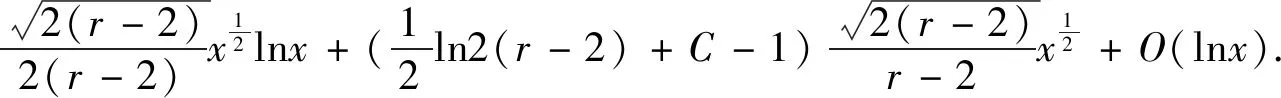
3.2 定理2的证明
对于任意给定的正数x>1,设M是满足
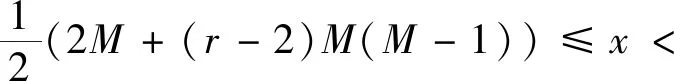
的正整数,由a(n)的定义及引理3有:
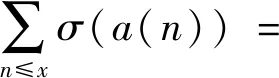
…+σ((r-2)t))+(σ(0)+σ(1)+…+
σ(M(r-2)))
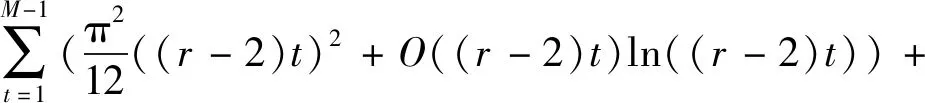
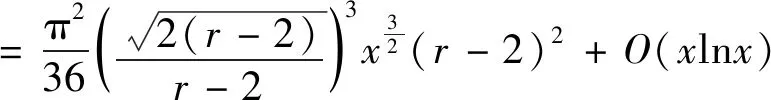
猜你喜欢
黑龙江大学自然科学学报(2022年1期)2022-03-29
今日农业(2021年11期)2021-11-27
中学生数理化·七年级数学人教版(2019年9期)2019-11-25
中等数学(2019年8期)2019-11-25
中学数学研究(广东)(2018年13期)2018-08-11
中等数学(2018年12期)2018-02-16
中国三峡(2016年5期)2017-01-15
中学生数理化·七年级数学人教版(2016年8期)2016-12-07
现代企业(2015年4期)2015-02-28
科技视界(2015年35期)2015-01-10

