基于自适应多特征匹配的移动机器人SLAM研究*

茹淑慧, 王红旗, 唐 浩

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

0 引 言

近年来，同时定位与地图构建(simultaneous localization and mapping,SLAM)技术在机器人领域受到了广泛的关注和应用，被研究者普遍认为是实现机器人完全自主的关键[1]。其中，最常用的扫描匹配技术是标准迭代最近点(iterative closest point,ICP)算法[2,3]。ICP算法通常使用相邻两帧扫描数据点集进行匹配[4]，但是由于扫描数据点数量较大，导致该算法计算负荷较大，收敛速度较慢。许多学者对ICP算法进行改进，大都从扫描数据中提取特征，利用特征匹配来求解相对位姿。文献[5]采用从扫描数据中提取特征点进行ICP匹配，减少了匹配时间，提高了SLAM算法的快速性，但该方法适合于具有清晰的线段或角点特征的多边形结构化环境。文献[6]采用了一种基于几何统计特征的全局扫描匹配方法，利用“试探—验证—求解”(probing verification solution,PVS)的匹配策略获得扫描之间的相对位姿。文献[7,8]采用多特征关联方法来提高匹配的精度，但该方法在匹配策略中分配固定的加权值，在复杂多变的环境中缺乏适应性。

本文采用激光扫描仪对环境进行扫描，获取扫描数据点集。首先对扫描数据点集进行区域分割，提取区域的多特征信息；然后利用区域的多特征信息对ICP算法的匹配策略进行改进，得到与下一帧区域的相关性，并自适应调整多特征的加权系数从而保证ICP匹配的精度，最终实现了移动机器人的同步建图与定位。

1 扫描匹配的问题描述

扫描匹配算法的地图构建与定位是对相邻两个扫描数据点集进行匹配[9]，得到两组点集之间的旋转矩阵和平移向量(R,T)。扫描匹配算法的示意图，如图1所示。

图1 扫描匹配算法示意

设Pk-1={Pi,k-1(xi,k-1,yi,k-1)|i=1,2,…,n}为k-1时刻的扫描数据点集,Qk={Qj,k(xj,k·yj,k)|j=1,2,…,m}为k时刻的扫描数据点集。

匹配前，先将k时刻的扫描数据点集转换到k-1时刻的坐标下，令Q′j,k=RQj,k+T，然后以式(1)中E(R,T)达到最小值为评价标准，求解位姿变换参数R,T

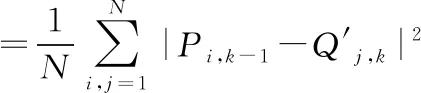
(1)

式中R(Δθ)为两组点集的旋转矩阵，Δθ为旋转角度，T=[Δx,Δy]′为两组点集的位移向量，Pi,k-1和Qj,k为两组点集中的对应点，N为对应点的数目。

2 基于自适应多特征扫描匹配的SLAM方法

2.1 自适应变阈值分割方法

原始扫描数据量较大，而且还存在噪声点，直接进行扫描匹配会影响定位与地图构建的实时性，因此，应先对扫描数据进行区域分割。为了保证在不同距离和角度都能正确对原始扫描数据进行分割，采用了自适应变阈值分割方法[10]。

由区域分割得到k-1时刻的区域分割点集Ak-1={Ai,k-1|i=1,2,…,r1}和k时刻Bk={Bj,k|j=1,2,…,r2}，其中r1和r2为区域的个数。

2.2 多特征的相似度

为了提高ICP算法效率，利用区域特征信息用于匹配，可以大大减少计算量。由2.1节得到区域点集Ak-1和Bk，选择每个区域的中心坐标(xc,yc)，角度α=arctan(yc/xc)，宽度w=|max{Δy}|，长度l=|max{Δx}|来表征区域的多特征信息。综合考虑区域的多特征信息，只有与目标“相似”最大的那个区域被认为与其相匹配。

1)区域中心特征相似度

(2)

式中SDis为区域集Ak-1中第i个区域的中心坐标和区域集Bk中第j个区域的中心坐标的相似度。SDis越大，两个区域就越靠近。距离最远的区域相似度定义为0。

2)区域角度特征相似度

(3)

式中Sα为区域集Ak-1中第i个区域的角度和区域集Bk中第j个区域的角度的相似度。Sα越大，两个区域就越靠近，角度差异最大的区域相似度定义为0。

3)区域长度和宽度特征相似度

(4)

(5)

式中SL和SW分别为区域长度和宽度特征的相似度。两个区域之间的长度或宽度特征相似度越大，差异就越小，长度或宽度差异最大的区域相似度定义为0。

在得到区域的中心、角度、长度和宽度四个特征的相似度后，区域多特征的相似度为

(6)

2.3 特征相似度权重系数

式(6)在计算区域多特征相似度时，特征的权重系数是固定的，在复杂多变的环境中适应能力较差，为此，本文使用自适应特征相似度加权系数。

在每次扫描匹配时，根据初始权重系数，得到初始匹配区域集

C=(Cl=(Ai,k-1,Bj,k)|i=1,2,…,r1,

j=1,2,…,r2,l=1,2,…,r3)

(7)

式中l为匹配区域的个数，由C中匹配区域的中心坐标，经式(1)计算，得到相邻两组点集之间位姿变化Δx,Δy,Δθ。

区域集单项特征的变化量分别为

(8)

当特征变化较大时，应分配更小的权重系数，即，特征的权重系数与特征变化成反比。特征的权重系数为

(9)

2.4 同时定位与地图构建

经匹配后，可以得到机器人k-1和k的位姿变换Δpk-1(Rk-1,Tk-1)。设以第1次扫描所建立的局部地图M1作为全局的初始地图[5]，第k次扫描时的局部地图为Mk，机器人的位姿为pk，全局地图为Mall，机器人的初始位姿为p1=(0,0,0)′。则第k次扫描时机器人的位姿pk为

pk=Δp1+…+Δpk-1

(10)

第k次扫描的局部地图Mk坐标变换到全局地M′k为

M′k=Δp1+…+Δpk-1

(11)

全局地图为

Mall=M1+M′2+…+M′k

(12)

3 仿真实验验证与分析

仿真中所采用的数据由悉尼大学发布的数据集，具有丰富的结构化和非结构化特点。为进一步研究算法的性能,分别用标准ICP匹配算法、本文算法对以上数据进行匹配。将标准ICP算法作为基准，从匹配误差和迭代次数两方面对以上两种算法进行定量比较。

3.1 匹配误差性能分析

分别用标准ICP算法和本文算法对匹配的误差进行比较。从激光扫描数据集中随机选取连续的 1000 帧数据，误差以mm计算。结果如图2所示。

图2 匹配误差对比

由图2看出: 本文算法在匹配误差上小于标准ICP算法。标准ICP算法考虑了所有的扫描点，甚至考虑了离群点，必然会导致对应点的误匹配，影响匹配精度。本文算法主要是基于区域的自适应多特征进行匹配，明显的提高了匹配精度。

3.2 迭代性能分析

分别用标准ICP算法和本文算法对迭代次数进行比较。从激光扫描数据中随机选取连续的 1000 帧数据，将匹配的最大迭代次数均限制为50次。结果如图3所示。

由图3可以看出,本文算法在迭代次数上要远远小于标准ICP算法。标准ICP 算法的迭代次数是11.49; 本文算法的迭代次数5.34。标准ICP算法中对应点如果选取正确，迭代次数就会很少，如果对应点选取有误，迭代次数就会很多。本文算法仅仅选取区域的中心点坐标来参与运算，减少了匹配的数据量，大大减少了运算次数。

图3 迭代次数对比

3.3 地图建图结果验证

用标准ICP算法跟本文算法分别进行定位与地图构建，实验对比结果如图4所示。其中黑线为激光扫描仪的定位结果，周围轮廓为建立的环境结构图。可看出本文算法比标准ICP算法效果更好。

图4 二种算法地图建图结果

4 结束语

针对标准ICP算法实现同时定位与地图建图计算量大的问题，本文采用了一种基于自适应多特征匹配的SLAM方法。利用区域的多特征用于匹配，可以大大减少计算量，然后，自适应调整多特征的加权系数从而保证ICP匹配的精度。通过以上实验分析可以看出,本文算法在匹配误差上要小于标准ICP算法,在迭代次数上远远少于标准ICP算法。因此，本文算法能够有效地完成同时定位与地图构建。